基于节点多约束的支架动力学稳定分析
王雪鉴, 王毅恒, 孙新坡
(四川轻化工大学土木工程学院,四川 自贡 643000)
0 引言
钢管模板支架主要由立杆、水平杆、竖向剪刀撑、水平剪刀撑等通过节点相互连接形成的杆系结构,其具有非常强的整体结构稳定性,当荷载作用到立杆上时,与立杆通过节点相连的斜杆、水平杆都会起着帮助分担荷载的作用。前人提出针对支架特点的单个立杆计算模型来简化分析,但是其建立的计算模型往往只考虑了其中一种约束的影响,而连接节点具有半刚性多方向约束的特点,国内外学者通过数值模拟和试验研究节点的多方向约束特性,说明了其对立杆稳定性贡献不可忽视,因而仅仅只考虑节点某一种约束的计算模型是不符合实际情况的。
多节间连续压杆模型首次由赵滇生等[1]提出用于扣件式高支模分析模板支架体系,并运用能量法得到了其临界荷载为无弹簧支座临界荷载值的2倍,说明了节点水平位移约束对立杆稳定性的贡献;之后张春凤等[2]对碗扣式高支模体系的多节间连续压杆模型进行了细致的分析,运用有限元模拟得到失稳曲线,详细运用了力学方法推导了多节间连续压杆的临界荷载计算公式并在考虑剪刀撑高度、扫地杆高度、架体高度、顶托高度、和杆件自身的初始缺陷的情况下,又对临界荷载公式进行了修改,得到了考虑以上多个因素的荷载求取公式;但上述研究中只考虑了水平杆和扣件节点的水平位移约束,对于支架的稳定性计算缺少了节点的其他位移约束;半刚性如果仅仅只针对一种约束,在其他约束方向上假设为全刚性会夸大其约束效果,使计算结果偏大,并且水平斜杆和水平剪刀撑并不能显著提高承载力;文献[3]中通过对多个静力试验模型分析,总结出扣件连接和扣件的拧紧力矩对扣件式满堂脚手架承载力有显著影响的结果。因此,对模型计算的修改优化非常有必要。
文中通过借鉴动力学分析[4,5]的方法,避开复杂结构的内力分析,对现有的仅弹簧支座模型进行公式推导,考虑小变形位移假设得到临界荷载公式,证明其方法的可行性并得到了结构大变形失稳位移曲线的公式计算方法,与已有结果进行比对,展望其未来的可行性;根据节点的主要方向约束效果为Y方向的转动约束和轴向X方向的位移约束,对多节间连续压杆模型进行优化,参考相关文献对于约束刚度取值的研究成果,完善多节间连续压杆的计算模型的研究。
1 动力分析
1.1 弹簧支座多节间连续压杆模型临界荷载推导
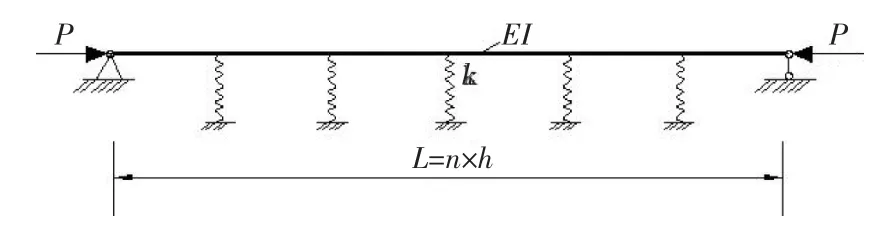
图1 有多个弹簧支座的多节间连续压杆
设杆件的全长为L=nh,h表示相邻两个支座之间的距离,坐标选为杆件中点X轴为水平方向,Y轴为与水平杆垂直方向。


1.2 验证动力分析


1.3 考虑杆件为较大变形时的失稳曲线

2 压杆模型优化
2.1 半刚性节点多方向约束分析
钢管模板支架体系的节点连接有铰接,刚接和半刚性连接,其中铰接计算并未考虑节点具有一定的抗弯刚度,刚接计算又过度夸大了节点的转动约束。相关文献[6]-[12]的研究中指出节点处于半刚性状态且对支撑模架的稳定承载力的影响非常显著,不能忽略;而且碗扣式和扣件式的节点抗弯刚度不同,其稳定性的承载力也必然受其影响,更不能直接相互套用。相关学者在节点多参数模拟法中提出扣件式节点的多方向约束性能,列出了全刚接条件下水平杆对立杆约束的6个自由度的理论刚度,提出扣件和钢管壁存在滑移、纵横扣存在转动导致半刚性状态的折减机制和折减系数;确定扣件节点6个约束的影响效能效果,扣件节点位约束的多参数取值见表1。
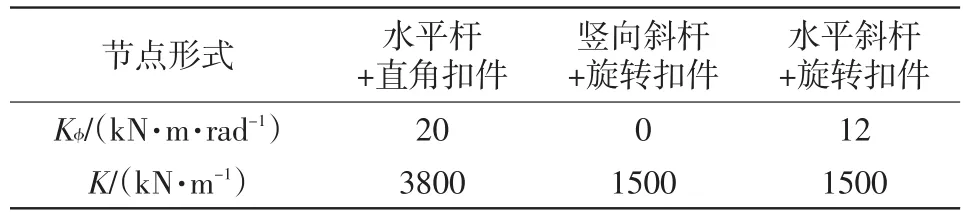
表1 扣件多方向的X方向和Y方向位移
对于双排扣件脚手架的承载力研究中运用线性模型给出了角位移与弯矩计算公式,提出双排扣件节点转动的非线性不显著的结论;通过试验得出角弹簧刚度计算并且最后取值为K=15.17kN·m/rad,对于转角刚度的求解减少了非线性因素;在研究扣件式支模架承载力试验中通过在节点上施加不同力矩试验得出了具体公式表明了弯矩与转角的关系,其中n为形状参数,Rki为初始刚度,并且试验结果为46.85kN·m/rad;针对碗扣式脚手架的抗弯性能研究对碗扣式节点抗弯能力进行了试验,提出了碗扣式节点弯矩-转角的关系存在明显的非线性关系,总结了国内外大量试验数据的回归拟合关系,并提出全新的试件平均转动刚度取值为52kN·m/rad,使用久了的试件转动刚度取值为27kN·m/rad;程海潜等通过实际工程案例和数值模拟,提出碗扣式临时支撑结构承载力大小与其节点刚度值大小成正比的结论;对于直角扣件脚手架的试验研究中提出水平杆直角扣件拧紧力矩为T=40N·m时,扣件转动刚度为19.8674kN·m/rad;文献[12]中通过对多个静力试验模型分析,根据试验结果得出扣件节点的转动刚度取值为22.58kN·m/rad和扣件抗滑移性能的不均匀系数取值为1.51。文献[2]还对碗扣式满堂支架整体进行分析,选取结构易发生的反对称失稳,对简化钢架结构进行分析得弹簧刚度:
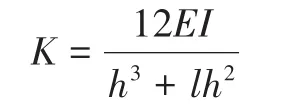
式中,h为立杆与立杆之间的跨度,并与扣件自身的抗滑移性能比较,取两者最小值。
文中依据相关文献对节点约束性能的分析,针对水平杆、剪刀撑和斜杆的节点位移约束等效简化为弹簧刚度为的弹簧支座,其取值考虑相关节点水平轴向抗滑移性能和其高支模体系结构的特点综合分析;角弹簧具有提供力矩但却不等于刚接的效果能与半刚性有一定程度的相似,综合分析采用文献中提出的转角刚度的关系和试验分析,提出用角弹簧模拟节点弯矩与转角之间的关系。
2.2 具有角弹簧的多节间连续压杆模型优化
通过对半刚性节点转动约束的线性关系的综合考虑,对多节间连续压杆进行优化。在立杆与弹簧支座之间增加具有等效的角弹簧连接,角弹簧可提供一定的抗弯刚度模拟半刚性节点转动约束。用K表示角弹簧抗弯刚度,其转角与弯矩之间的关系为M=K·θ;考虑扫地杆与剪刀撑的基础上,在立杆的底部支座处和铰接处同样设立角弹簧模拟节点转动约束。

3 验证模型计算理论
部分运用上述推导的计算公式验算相关文献中的计算结果,因为碗扣式支架和扣件式支架节点连接不同,约束性质和约束刚度取值不一样,文中将分开验算两种节点类型的支架,参考相关研究成果给出的约束刚度,验证模型计算的合理性;在计算支架稳定承载力的基础上,运用文中提供的分析思路方法给出支架失稳位移的计算值,并与电算值进行比对。
3.1 碗扣式支架试验结果比对
采用上述临界荷载计算公式来进行验算,取碗扣模板支架中的计算结果和碗扣式支架试验结果,运用文中计算公式重新验算结果进行比对。综合考虑有关文献中碗扣式节点半刚性分析,选取文献[10]中碗扣式临时支撑结构节点刚度值范围在25~35kN·m/rad。
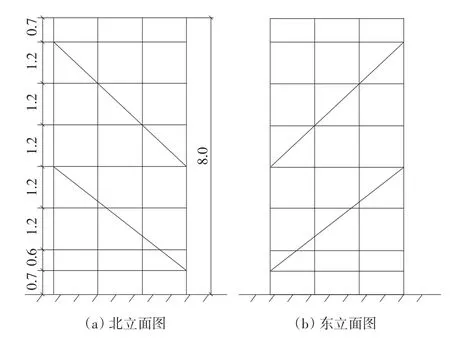
图2 试验方案布置图(单位:m)
立杆平面4×4布置,架体高H=8m,步距h=1.2m,其中,步距×层数为0.6m+1.2m×5,立杆的间距为l=1.2m,其试验结果为67.5kN。忽略扫地杆高度、悬臂长度等高度系数,取验算的弹簧刚度为K=50kN/m,则失稳时达到临界荷载的最小半波数:

n取整数为n=2;取K 为25~35kN·m/rad,则临界荷载F=60.75~70.75kN
与试验结果67.5kN相比,验证计算的可行性,其实际精确值需考虑碗扣式节点的实际转动刚度取值。
3.2 扣件式支架结果对比

表2 不同弹簧刚度的立杆屈曲荷载 kN
根据相关文献中试验结果综合分析,根据试验的时间、条件和严谨性,取文献[6]中的值K为20kN·m/rad则验算临界荷载结果见表3。

表3 验算不同弹簧刚度的立杆屈曲荷载 kN
与实例计算结果和有限元模拟结果相比较,文中计算的结果与已有的计算和有限元的数值模拟结果接近,说明了考虑转动刚度的计算模型具有可行性和正确性。
3.3 位移监测预警值的确定
比对计算用文献[13]的试验为对象,运用文中的1.3部分的推导计算位移值公式进行比对分析。

表4 碗扣式钢管脚手架预警值

表5 碗扣式钢管脚手架公式计算预警值
文中计算结果与文献中结果对比分析,其存在数据差异的原因可能有:
(1)未考虑碗扣式钢管脚手架的初始缺陷、扫地杆高度、悬臂长度以及架体和剪刀撑的修正。
(2)文中的计算模型仍为二维模型,针对多方向的失稳位移需要建立三维模型计算。
(3)对于简化弹簧刚度的取值还存在误差。
文中的计算结果与电算结果对比结果说明该方法具有一定的可行性,但其存在误差还需要进一步研究。
4 结语
文中通过对多节间连续压杆和半刚性节点进行分析,运用了动力学振动分析法得到多节间连续压杆的失稳曲线和临界荷载,得到了结论如下:
(1)验证了动力学振动分析对高支模体系的可行性并通过动力学方法给出了多节间连续压杆的临界荷载公式和考虑大变形的失稳位移曲线计算。
(2)从支架节点的多约束角度出发,对扣件式以及碗扣式的主要转动约束刚度取值进行了综述分析,提出用角弹簧来模拟转动约束的存在两种约束的计算模型方法,对比各个试验的情况选取适合约束刚度。
(3)通过试验结果和实例有限元结果相比较,验证了考虑角弹簧计算模型的可行性,其计算关键在于转角刚度的取值;对失稳位移的计算方法存在可行性,但是对于实际工程情况必须对其进行相应系数修正,应在计算时综合考虑影响因素。文中的方法可以为支架计算的研究提供一种新的思路以及为类似的支架工程的计算提供一种参考方法。
文中研究的仍为二维平面简化模型,针对支架节点的多个方向的约束可建立三维的整体模型并增加相应关键约束进行分析。

