风电叶片双点疲劳加载同步激振控制*

朱书臻，宋勇达，郭文哲，丁向富，蒋明真，黄雪梅

(山东理工大学机械工程学院，淄博 255000)

0 引言

能源是经济社会发展的重要物质基础，也是碳排放的最主要来源，根据国家2030年前碳达峰行动方案，要坚持安全降碳，在保证能源结构的前提下，大力实施可再生能源，加快构建清洁低碳安全高效的能源体系。要坚持海陆并重，推动能源协调快速发展，完善海上风电产业链，鼓励建设海上风电基地。随着海上风力发电的进一步发展，风电机组的装机容量不断上升，风电叶片的设计尺寸也随之增大。风电叶片的使用寿命直接关系到风力发电的经济成本，疲劳破坏又是风电叶片的主要失效形式[1-2]，因而风电叶片进行疲劳测试是对其寿命检测的一种有效方法。由于风电叶片规模越来越大，为达到叶片共振振幅所需的驱动力也越来越大。使用单点疲劳激振加载方式，受电机功率等的影响，加载力难以满足共振条件，很难达到试验要求。液压强制位移型疲劳加载，虽然能满足加载力的要求，但存在加载效率低、试验成本高等缺点。因此采用多套激振器在多点进行同步加载，可以加大激振力使风电叶片更易产生疲劳共振，缩短试验时间、节省能量。

双点惯性疲劳加载是针对现有单点疲劳加载驱动力不足的而提出的一种新型疲劳加载方式，通过控制在风电叶片不同位置固定的两个偏心质量块的同步转动而产生的激振力实现对风电叶片的疲劳加载。两激振器同时激振相当于加载电机的功率提高了一倍，大大提高了加载力，可满足对大型风电叶片的疲劳检测要求。由于两个激振器的参数不可能完全相同以及试验过程中外界环境和载荷扰动的影响，导致两激振器不可能完全同步，因此研究风电叶片双点疲劳加载的同步控制策略具有重要意义。目前，国内外学者提出了若干应用于同步控制方面的策略，张磊安等[3]建立滑膜变结构算法，研究风电叶片疲劳激振耦合特性，提高同步性能；廖高华等[4]利用小参数周期平均法研究叶片的振动同步条件；ELKENAWY等[5]利用全状态神经网络观测器，研究对角回归神经网络的自适应控制效果；唐翠微[6]提出一种混合神经网络算法，抑制机械手坐标数据梯度膨胀问题，从而提高轨迹控制的连续性、稳定性。以上提出的各种控制算法无法消除机电耦合，同时疲劳测试振幅存在波动，同步误差和跟随误差难以达到控制要求。

因此，本文针对风电叶片双点疲劳加载同步控制问题。将对角回归神经网络控制算法，引入到交叉耦合控制策略中，克服了外界载荷扰动、工况恶劣等的影响。并通过仿真验证其有效性。试验结果表明，该算法控制效果好，显著提高了系统的同步性能、鲁棒性和稳定性。

1 双点疲劳试验加载方案

风电叶片双点激振疲劳加载系统主要由动力激振系统、控制系统、检测系统组成。风电叶片通过叶片上预埋的螺栓固定在试验台的法兰盘上，两个相同的激振器安装在叶片不同位置上的夹具上。激振系统主要包括：减速电机、偏心质量块、配重块、变频器等组成。叶片疲劳试验时，两个减速电机通过带动偏心质量块在叶片的展向或者弦向以叶片的固有频率做同步正弦运动，施加正弦激振力。控制系统主要由上位机、控制器和控制算法组成，上位机采用Labview语言编写主要完成人机交互、数据采集及数据存储等工作。检测系统是通过在叶片上粘贴应变片测量叶片不同位置的变形。加载方案如图1所示。

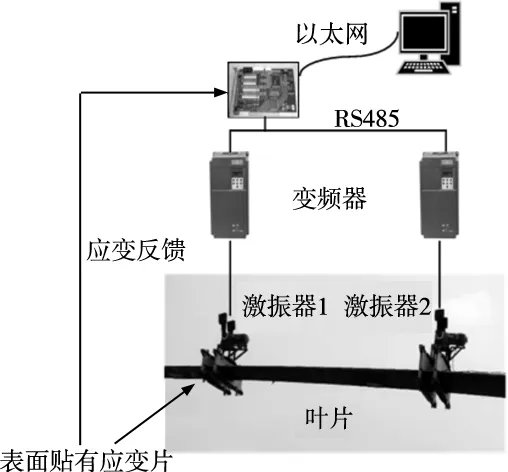
图1 两点疲劳加载试验方案

2 交叉耦合控制器设计

风电叶片的双点疲劳测试为双激振器同步加载。由于两激振器的参数不可能完全相同，且设备在外界环境的影响下很难实现两激振器的位置和速度上完全达到同步，因此，本文设计交叉耦合控制器使两个激振器联合成一个完整的闭环控制系统，从而提高两个激振器的同步性。其主要是对两个激振器的偏差耦合引入控制器，对每个控制器进行速度补偿来消除两个控制器之间的同步误差，控制策略如图2所示。

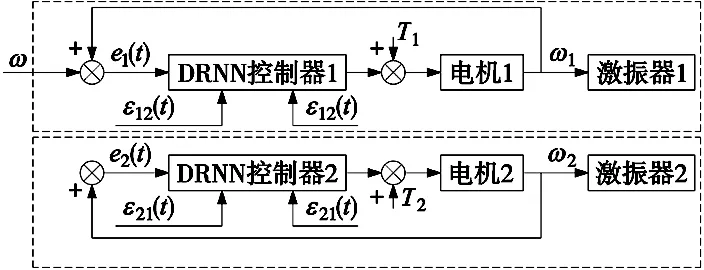
图2 基于DRNN神经网络的交叉耦合控制策略

其中，ω是系统的设定转速；ω1、ω2分别是电机1、电机2的跟踪转速；T1、T2分别为激振器1、激振器2的外界负载扰动；e1、e2分别为两个激振器的跟随误差；ε12、ε21分别为两激振器的同步误差。

由图2可知，要保证两激振器的同步性能完好，要使同步误差均趋于0，此时：

(1)

3 DRNN神经网络控制器设计

与静态神经网络相比，对角回归的神经网络具有更好的处理动态问题的能力。其输入层和输出层之间没有回归元，隐含层为具有内反馈的神经单元，网络模型可以更为简单，其基本结构如图3所示。

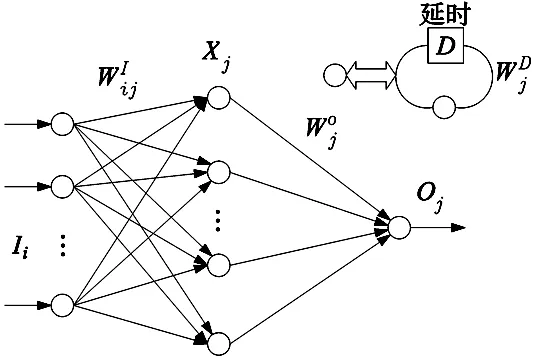
图3 对角回归神经网络结构

(2)

式中，f(·)为Sigmod函数。

对于风电叶片双点疲劳测试的同步转速控制系统而言，激振器的转速是控制电压所控制减速电机的输出力矩与外部干扰力矩综合作用的结果。为此设计的基于DRNN神经网络的同步控制算法能及时获取系统输出和指令信息以及外部干扰力矩相关信息，因而做到同时提高系统的同步控制精度、快速性、和鲁棒性。其控制方案方框图如图4所示。

图4 基于DRNN神经网络同步控制算法

由于系统的外部干扰引起的负载力矩为T1；系统的给定转速为ω；输出转速为ω1；经过归一化处理后得到DRNN控制器的输入向量为：

I=[I1I2I3]T
I=[ω(t-1)ω1(t-1)T1(t-1)]

(3)

DRNN控制器的输出为：

O(t)=un(t)
un(t)=f[ω(t-1),ω1(t-1),T1(t-1)]T

(4)

此控制算法中，DRNN的误差信号为PID控制器的输出uc，通进一步训练，使误差信号趋于0，进而DRNN控制算法逐步代替PID算法。选取DRNN神经网络控制算法的权值更新策略为：

(5)

依据链式法则以及梯度下降法得，任意权向量的迭代算法：

(6)

式中，η为权向量W的学习速率。

假定DRNN神经网络输出对任意权向量的变化率为：

(7)

将上式代入式(2)得：

(8)

式中，

(9)

将式(7)、式(8)代入式(5)可得输入权、输出权、回归权的迭代算法。为使DRNN神经网络控制控制算法进一步适应风电叶片双点激振疲劳测试系统，加快收敛速度，选取输出层具有较高的学习速率，输入层和回归层的参数保证控制算法不振荡，依据动态误差反馈算法和链式法则，运用梯度下降法则得到各权值层的迭代算法：

输入层：

(10)

回归层：

(11)

输入层：

(12)

式中，η0为输出层学习速率；a0为输出层权值动量因子；ηD为回归层的学习速率；aD为回归权值动量因子；η1为输入层的学习速率；a1为输入层权值动量因子。

为进一步保证DRNN神经网络控制算法在学习阶段的稳定性和学成后的鲁棒性，控制系统输出为：

u=un+uc

(13)

因此，基于对角回归的神经网络控制的控制算法，主要通过对系统动态问题的处理能力来估计系统的广义逆模型[10]。运用转速指令、负载转速、外界干扰力矩作为控制输入，既能获取足够的系统信息，又能对系统进行预测，达到微分补偿效果。进而提高系统的同步控制性、稳定性、鲁棒性。

4 现场试验分析

为了验证基于对角回归神经网络的交叉耦合控制算法在全尺寸风电叶片双点疲劳测试中的同步控制效果，根据以上设计方案，完成了疲劳试验现场的搭建，现场试验参数如表1所示。

表1 现场试验参数

根据以上参数，采用传统PID同步控制策略对85 m风电叶片进行双点疲劳测试，试验过程中两电机从静止开始运行到额定转速。由此得到两激振器电机的速度曲线和同步误差曲线。

由图5和图6可知，传统PID同步控制策略两激振器存在较大的同步误差和跟随误差，其最大转速同步误差大于30 r/min。因此，难以满足全尺寸风电叶片疲劳测试的控制精度和加载要求。

图5 传统PID同步控制策略转速曲线 图6 传统PID控制同步误差曲线

采用基于对角回归神经网络的交叉耦合控制策略的现场试验结果如图7和图8所示，其中图7为叶片40 m处振幅与时间的关系曲线。图8为两激振器在其控制策略下的相位差曲线。

图7 叶片振幅与时间关系曲线 图8 交叉耦合控制相位差曲线

根据图7可知，叶片振幅随着时间的推进，振幅逐渐达到稳定，风电叶片实现共振。并且振幅稳定在0.50 m。根据图8得，相位差控制在±3°左右，其波动较小，满足风电叶片全尺寸疲劳测试要求。

根据图9和图10可知，该控制算法能使两激振器电机转速较好的跟随控制信号。两激振器同步误差和相位差在0附近做微小波动，使最大转速同步误差控制在11 r/min之内。该算法能够自动调节同步速度偏差。相对于传统PID同步控制算法，两激振器的同步控制精度提高了36.67%，展现出来该控制算法良好的同步控制精度、鲁棒性和稳定性。因此，对该设计方案和本文提出的控制策略得到了有效的现场试验验证。

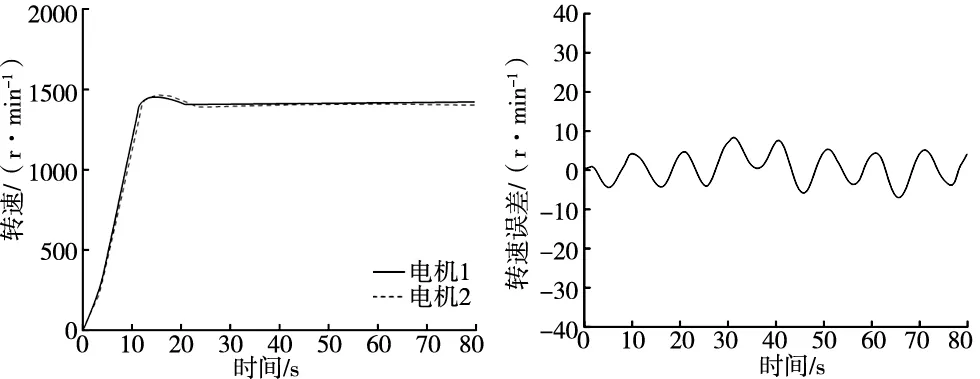
图9 交叉耦合控制策略转速曲线 图10 交叉耦合控制同步误差曲线

5 结论

(1)对疲劳测试系统控制算法进行设计，提出了基于DRNN神经网络的交叉耦合同步控制算法，将该算法与传统PID同步控制算法进行对比，结果表明，该算法具有较小的同步误差和跟随误差。

(2)通过搭建试验平台，进行现场测试得出，该控制系统能够较好地保证电机转速同步、且受外界干扰影响小，系统具有良好的鲁棒性、快速响应能力和同步控制精度。