基于注意力QRNN的离散车间生产瓶颈预测*

汪伟丽，郭 宇，刘道元，高瀚鹏，杨志伟

(1.南京航空航天大学机电学院，南京 210016；2.北京星航机电装备有限公司，北京 100074)

0 引言

经济社会的快速发展对企业的生产能力提出了更高的要求，而离散制造车间存在的瓶颈现象严重地制约了系统的有效产出[1]，影响了车间的生产效率，因此如何准确描述并预测作业车间的生产瓶颈是当前的研究重点。

针对瓶颈定义问题，部分学者通过生产系统中工作负载最大的设备[2]、对整体系统吞吐量影响最大的设备[3]等来描述瓶颈。在瓶颈识别方面，REID等[4]对制造单元的生产能力和生产需求进行度量以识别瓶颈；翟颖妮等[5]设计正交实验识别生产中的系统瓶颈；SUBRAMANIYAN等[6]开发了一种实时数据驱动的平均活动周期瓶颈检测算法。瓶颈定义用于描述瓶颈单元，瓶颈识别用于检测瓶颈单元，但瓶颈识别一般是事后识别，此时瓶颈影响已经造成，而瓶颈预测是事前识别，对车间的生产调度更具指导意义。叶涛锋等[7]提出了一种利用队列图形评价和回顾仿真技术的瓶颈预测方法；LIU等[8]构建了瓶颈度与瓶颈指数来描述动态瓶颈特征，并建立了生产物流瓶颈预测模型。基于仿真建模的瓶颈预测方法，模型构建相对复杂，难以准确描述离散车间的动态情况。随着大数据分析技术在车间的应用，CAO等[9]提出了一种基于自适应网络模糊推理系统的瓶颈预测方法，可以准确预测主次瓶颈。HUANG等[10]提出一种基于深度学习的瓶颈预测方法，在案例中测试效果良好。数据驱动的预测方式，对车间数学模型的构建相对简单，但未考虑瓶颈问题的时序性，不利于做长期分析预测。杨昊龙等[11]提出的基于长短期记忆神经网络的瓶颈指数预测方法，实现了时间序列建模，但其串行计算方式在计算时长上不具备优势，且前述研究中对不同状态数据的利用程度相同，未能充分挖掘信息特征。

基于上述分析，本文提出了基于注意力机制的准循环神经网络(quasi-recurrent neural networks，QRNN)生产瓶颈预测方法，以QRNN网络的卷积结构提取特征信息、池化结构提取序列信息，减少了模型训练时间，引入的注意力机制充分发挥不同时刻的状态信息，提高了瓶颈预测精度。最后在某机加车间进行算法对比，验证了本文方法的优势。

1 离散制造车间的瓶颈问题描述

传统的瓶颈单元一般定义为负荷最大的设备、库存堆积最多的设备等，这种定义方式割裂了车间设备在生产过程中产生的因果关系，而离散制造系统是由多个不同加工功能的生产单元组合而成，各生产单元基于工件的工艺路线存在着一定约束关系，上游生产单元的生产效率影响着下游生产单元的任务产出，故以车间全局为研究对象，找到制约生产的关键单元，即为瓶颈单元。

本文将车间的加工工位，包含该工位的出入缓存区视为一个完整的生产单元，在实际生产过程中，生产单元既需响应上游工位传递的加工任务，也需满足下游工位所需的加工任务，因此，定义瓶颈值为生产单元满足上下游生产任务的综合能力的负值，瓶颈值最大的单元即为瓶颈单元。为方便后续描述，对车间的基本要素进行定义，如表1所示。

表1 车间基本要素定义

则t时刻，工位Mk瓶颈的表达式bottleneckk如下：

(1)

(2)

bottleneckk=-(-PA+NA)

(3)

式中，PA表示t时刻工位Mk的缓存区Bk内的工件的等待时间之和，PA越大，表示响应上游的能力越弱；NA表示t时刻工位Mk′的缓存区中来自工位Mk的工件的等待时间之和，NA越大，表示供给下游的能力越强，则工位Mk的瓶颈值如式(3)所示，bottleneckk越大，该工位的瓶颈值越大。

为刻画瓶颈单元制约车间生产时的运行状态，根据瓶颈问题特性，从车间采集全局变量与局部变量，共同构建成数据集，如表2所示。

表2 车间状态特征选取

实际车间的生产环境是动态变化的，且存在着各种扰动因素，使得车间的生产性能复杂多变，各单元的瓶颈值随之更新，生产瓶颈在时间维度上发生空间位置的转变，称之为瓶颈漂移现象。当扰动发生时，原本按照计划加工的制造单元的生产能力与设备负荷不再匹配，使得该环节的加工进度变慢，不能满足下一环节的生产需求，间接导致下一制造单元的瓶颈值偏离预期，成为影响下一环节的干扰因素，随着扰动因素的推进与变异，车间环境变得复杂难测，通过挖掘海量生产数据中的知识为找到瓶颈漂移的时变规律提供可能。

2 基于注意力机制的QRNN瓶颈预测模型

2.1 基于注意力机制的QRNN瓶颈预测框架

本文基于不同时刻、不同制造单元产生的数据，搭建瓶颈漂移预测框架，如图1所示，首先对车间运行过程中采集的历史数据进行预处理，将多条状态数据重组为一条具有时序信息的样本数据，然后基于上述的瓶颈量化公式，计算样本数据的瓶颈值作为数据标签，以处理后的时序数据作为模型输入，瓶颈值作为输出，通过QRNN网络的卷积结构与池化结构挖掘状态信息，并借助注意力机制有侧重地提取不同时刻的信息特征，训练后的模型可以根据当前时刻的实时数据，预测未来时刻各设备的瓶颈值。

图1 瓶颈漂移预测框架

根据QRNN预测网络的输入特点，将s+1条状态数据进行序列处理，重构为一条训练数据，其中每条状态数据的时间间隔差为Δt，则重组后的输入序列的表示形式如下：

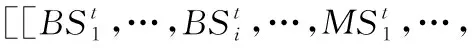
(4)

不同类型的状态数据存在着数值量级区别，为方便模型训练，对输入数据进行归一化处理，如式(5)所示，将有量纲数值变成无量纲数值，归一化后的数据质量有所提高，可以加快模型的收敛速度。

(5)

2.2 基于注意力机制的QRNN瓶颈预测方法

瓶颈预测模型的输入是时序数据，瓶颈漂移问题自身也具备时序性，因此针对瓶颈预测问题，采用时序预测方法。循环神经网络的特殊结构可以在数据预测时更好的拟合数据在时间序列上的特性[12]，但RNN网络模型易出现梯度爆炸与梯度消失等问题，LSTM提出的门控单元针对性的存储信息与遗忘信息，有效的解决了梯度问题，但LSTM对输入状态同等重视，且串行计算方式在训练时间上略显劣势。

本文提出了基于注意力机制的QRNN预测模型(AQRNN)，QRNN模型结合了CNN与RNN的网络特性，以CNN捕捉短期局部依赖关系，以RNN捕捉长期宏观依赖关系，将卷积添加到递归中，取长补短，达到了更好的效果。如图2所示，以CNN的卷积操作来提取序列数据的特征，卷积操作的跨时间步并行计算大大减少了循环体内的计算时间，以池化操作代替LSTM门控单元体系中的输入门，遗忘门和输出门，该单元的输出依赖于上一单元的输入，实现了时间依赖性。

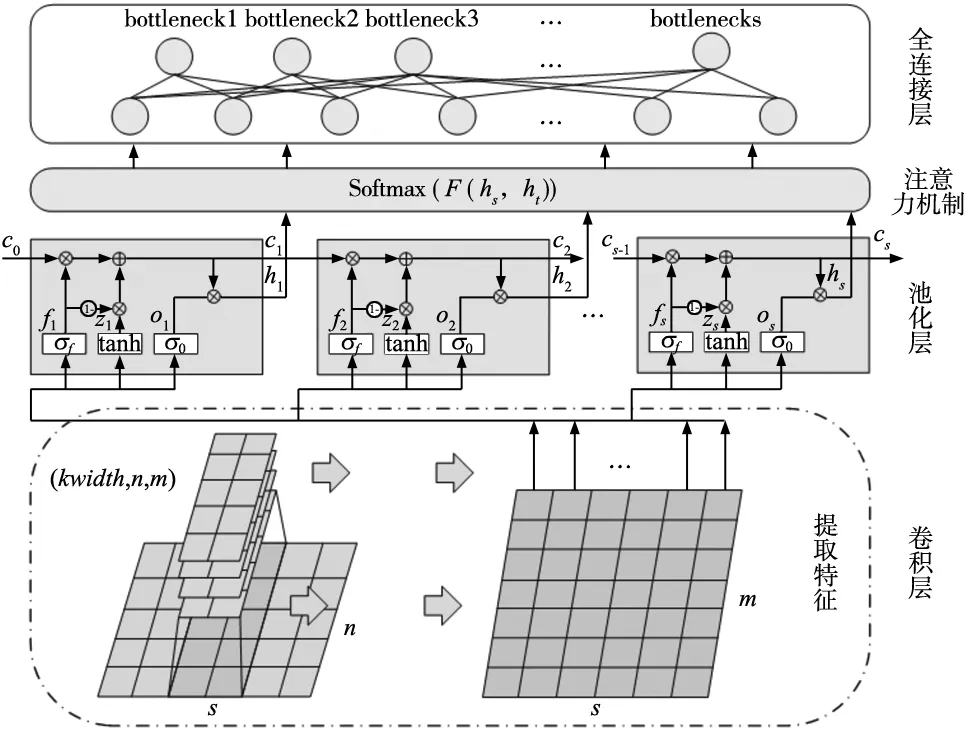
图2 基于注意力机制的堆叠QRNN的瓶颈预测方法

(1)前向传播。对于向量维度n，时间步长s的输入序列X，先通过卷积层，用一组m个宽度为k的滤波器进行特征提取，而后通过激活函数来获得池化层所需的门控向量序列，每个时间步t的计算公式如下。

(6)

(7)

(8)

式中，输入Xt的大小为[s,n]；WZ、Wf、Wo为滤波器权重，大小为[k,n,m]，滤波器沿着时间维度进行卷积计算，输出矩阵的大小为[s,m]，卷积过程共享参数，3个门函数的计算不依赖于上一个时刻单元的输出。

将提取后的向量序列输入到池化层，实现跨时间维度的计算，获取序列的顺序信息。为增强AQRNN的鲁棒性，将droupout应用到递归过程进行正则化，即在池化层的每个时间步随机选择一个子集，直接复制当前时间步状态到下一时间步，而不做计算。

ct=ft⊙ct-1+(1-ft)⊙zt

(9)

ht=ot⊙ct

(10)

F=1-droupout(1-σ(F))

(11)

式(9)中⊙表示Hadamard乘积，即对应位置元素相乘；ht、ct为输入序列第t个时间步的遗忘门与输出门；c初始化为0。式(11)中F为输入序列的遗忘门。

在池化层的输出序列上添加注意权重，给不同的状态赋予不同的权重以表征各状态的重要程度，使各状态在预测时发挥不同的作用。

(12)

(13)

式中，L表示AQRNN的层数；s表示时间步的长度。最后通过全连接层输出各生产单元的瓶颈值。

(14)

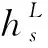
(2)反向更新。前向传播的最后输出是回归值，故损失函数取均方根误差(RMSE)，则loss表达式如式(15)所示。

(15)

式中，N为所取样本数；λ为L2正则化的超参数；Bottlenecki为第i条样本的所有工位瓶颈值矩阵，正则化可以避免网络过拟合。

(3)评价指标。采用均方根误差(RMSE)，平均绝对误差(MAE)，R方(R2)为评价指标，具体形式如下：

(16)

(17)

(18)

3 算法验证与案例分析

3.1 实验参数设置

本文选取某航天机加车间为例，该车间有6台含一定容量缓存区的加工设备，加工13种类型的工件，采集了15 264条数据，取13 737状态数据做训练集，训练AQRNN模型，经多次实验确定网络各参数，如表3所示。

表3 参数设置表

本文使用python语言与tensorflow框架搭建预测模型，工作站配置如下：处理器：Intel(R) Core(TM) i9-10980XE，显卡：NVIDIA GeForce RTX 3090，内存：DDR-4 32 G。

3.2 实验结果分析

为验证本文方法的有效性，在相同的实验环境下，选取LSTM，未加注意力机制的QRNN算法进行对比实验，数据预处理过程相同，经十折交叉验证法得本文算法的训练集与测试集损失结果，如表4所示，与其余算法的对比结果如图3和表5所示。

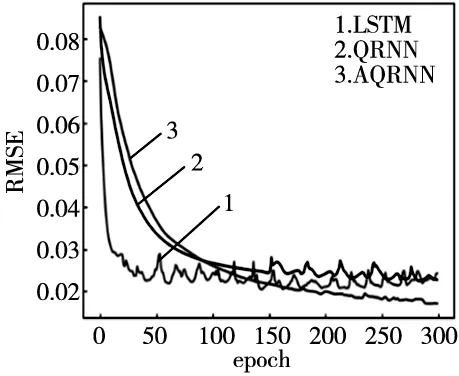
图3 损失变化对比图

表4 十折交叉验证损失值

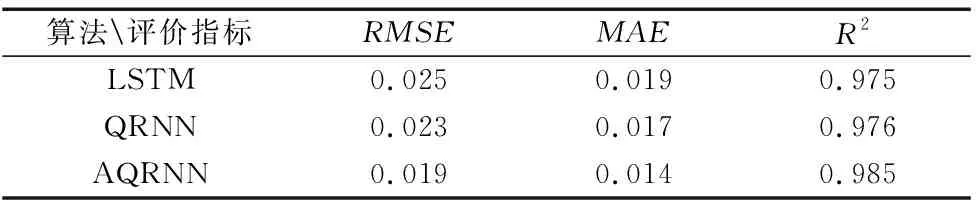
表5 评价对比表

由表4可知，AQRNN的损失变化在训练集和测试集上表现相似，由于训练时加入了正则化，有效的缓解了过拟合问题，且测试集损失值之间偏差较小，证明了本文算法的泛化性。由图3可知，AQRNN最终收敛到的损失值最低，LSTM与QRNN最终收敛到的损失值相似，相应的准确度可见表5，由于加入的注意力机制选择性的关注有助于当前任务的重要特征，提高了信息利用率，使得AQRNN的准确度高于LSTM与QRNN。

为验证本文算法在时间上的优越性，选取64，128，256三种不同的批量测试， AQRNN与LSTM两者的实验对比结果如表6所示。

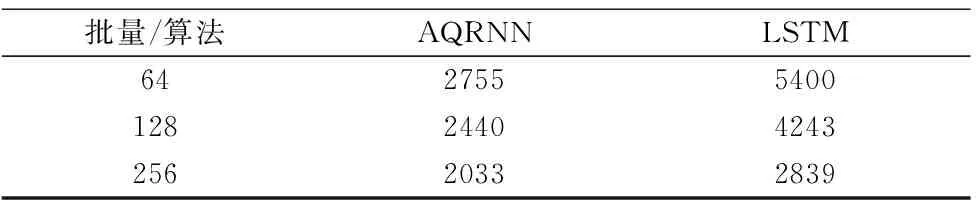
表6 运行时间对比表

由表6可知，由于AQRNN的网络结构采用卷积形式并行处理数据信息，缓解了采集序列信息时循环体内的计算量，使得AQRNN的运行时间远小于LSTM，随着批量的增大，二者的运行时间相应减少，AQRNN的减少趋势虽然小于LSTM，但运行时间始终低于LSTM。

取500个时间步分析预测结果，由图4可知，预测瓶颈单元与真实瓶颈单元基本拟合，瓶颈单元主要在工位1、工位3、工位5之间漂移，这三个工位的瓶颈值在相应的时间段内变化如图5～图7所示。

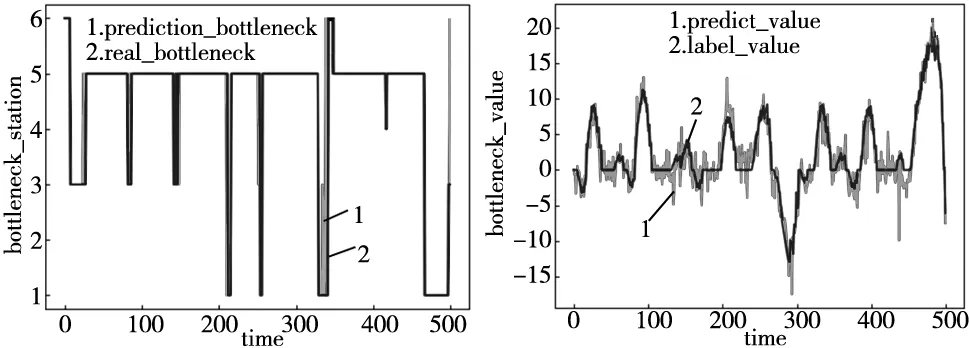
图4 瓶颈工位预测图 图5 工位1的瓶颈值变化图

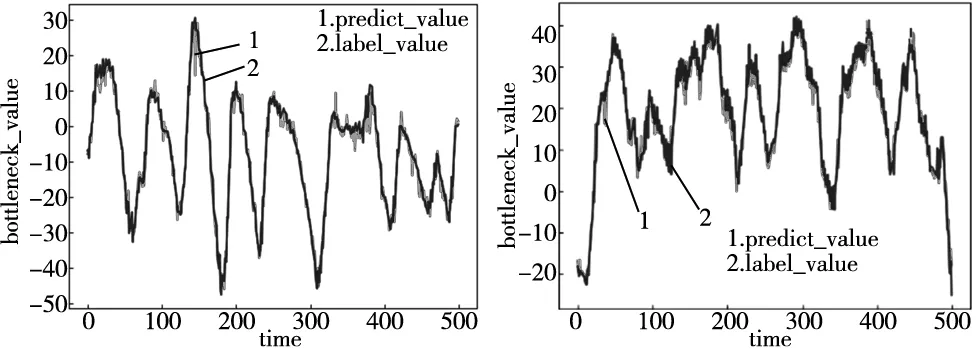
图6 工位3的瓶颈值变化图 图7 工位5的瓶颈值变化图

图5为工位1的瓶颈值变化，在部分时间段内，预测值与标签值之间略有偏差，但偏差较小，能够反映变化趋势，工位1的瓶颈值整体范围变化不大，该情形下工位1成为瓶颈单元的概率不高。图6为工位3的瓶颈值变化，工位3的预测值与标签值吻合度高，瓶颈值变化幅度较大，且为负的情况较多，由瓶颈量化公式分析，缓存区的待加工零件的等待时间较短，下游工位中来自工位3的零件的等待时间较长，工位3的加工能力相对较高，该情形下工位3成为瓶颈单元的概率相对较小。图7为工位5的瓶颈值变化，工位5的预测值与标签值吻合度较高，瓶颈值变化幅度较大，且长期处于高值状态，由瓶颈量化公式分析，工位5的缓存区的零件的等待时间较长，该工位的加工能力较弱，成为瓶颈的概率较大，后续的车间生产中对工位5要重点关注。

4 结束语

本文针对离散制造车间存在的瓶颈漂移现象，提出了基于注意力QRNN瓶颈预测方法。首先结合车间的生产特点，量化了车间瓶颈，定义了状态数据类型，而后分析了瓶颈漂移现象，并提出了基于注意力机制的QRNN瓶颈漂移预测框架，对生产数据进行序列处理，输入到预测模型中进行训练，融合的注意力机制充分利用了状态数据，训练好的模型可以根据实时数据预测未来不同工位的瓶颈值，帮助车间人员找到未来的瓶颈工位，最后在实例上进行实验分析，验证了算法的有效性和准确性。在后续研究中，可以对车间进行溯源分析，找到导致该单元成为瓶颈单元的干扰因素，帮助车间人员明确干预方向，缓解瓶颈单元带来的影响。