基于独立基线的GNSS网观测方案精准设计与实现

王爱生, 王正帅, 胡晋山

(江苏师范大学 地理测绘与城乡规划学院,江苏 徐州 221116)

0 引言

利用全球导航卫星系统(global navigation satellite system,GNSS)布设地面观测网已成为控制测量的主要手段[1-3].Snay[4]设计了用3台或4台接收机进行观测的方案,方案包括3个基本特点:1)网中每个点上都要设站,并观测相同的次数,且每次都使用不同的接收机;2)每一条边的观测次数都不超过1次;3)短边优先.Unguendoli[5]讨论了用5～8台接收机进行测量的观测计划,给出了时段数和多余基线数的计算公式.此后,GNSS网的设计基本上沿用Snay和Unguendoli的方法,只是在实际使用过程中有所简化:第一,不再强调每个点上都必须观测相同的次数,而是强调平均观测次数不得低于规定的重复设站数,且所有点的观测次数要均匀[6].第二,不再要求每次观测都使用不同的接收机,接收机可以在一个点上保持不动,但最好重新安置仪器和测量天线高[7].由于GNSS观测的高精度,因此,简化之后仍然能够保证控制网的精度和可靠性[6-12].然而,使用文献[4-7]的方法画出的图形一般比较复杂,如看不出哪些边是独立基线,哪些是同步环,哪些是异步环.为此,赵长胜等[13]展示了一种网图设计思路,即通过特征条件预先计算出控制网有几条独立基线,构成几个多边形;网图中只画出独立基线,所有的多边形都是异步环.基于文献[13]的设计思路,本文重点解决多边形有几条基线的问题,并在此基础上使用Matlab编写程序,能够自动生成控制网图形和自动拟定观测计划.

1 问题的提出

在实际操作时,由于不知道异步环究竟有几条基线,可能出现先画出的多边形基线数偏少、后画出的多边形基线数偏多的情况,从而导致设计出的图形不美观,在精度上也不利于全网的平均.因此，要设法计算出异步环的平均基线数,网中所有的异步环都按平均基线数来画.

2 异步环的平均基线数

把边界上的点连接构成外围多边形,基线数用s表示,则有aJ3=2J1-s,从而

(1)

其中:a为闭合环的平均基线数,2J1表示1条基线被使用了两次.

利用式(1)计算出来的a可能为整数，也可能为小数.如果a为整数,则全网只要画出J3个a边形即可;如果a为小数,则为了使多边形的边数相等,网中只能出现两类多边形:一类的基线数为a向下取整;另一类的基线数为a向上取整.如图1是一个GNSS控制网,n=10,令r=4,m=1.6,可得c=4,J1=12,J3=3,s=7,按照式(1)可计算出异步环的平均基线数a=5.7.

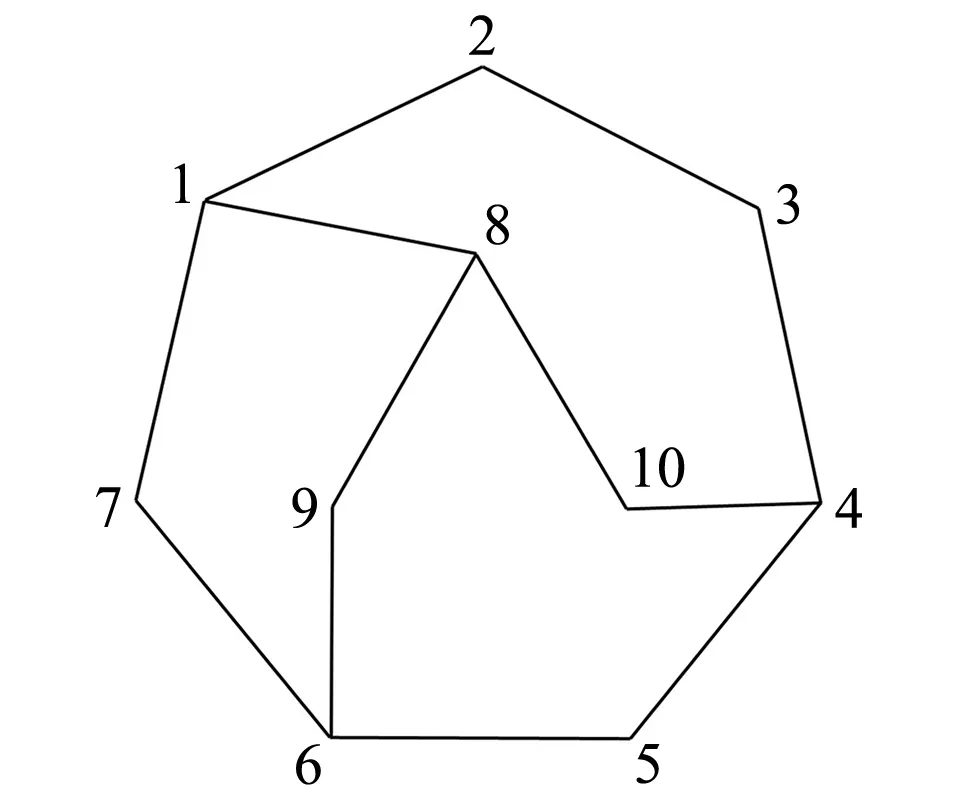
图1 GNSS控制网

3 两类多边形的个数

若a为小数,则用ad表示对a向下取整,用au表示对a向上取整.设网中有t个多边形,其基线数为ad;有g个多边形,其基线数为au,显然有

adt+aug=2J1-s.

(2)

由于

g=J3-t，

(3)

将(3)代入(2),可得

t=auJ3-2J1+s.

(4)

将(3),(4)应用于图1,可得t=1,g=2.因此,只要在图1网中画出1个五边形和2个六边形即可.

4 拟定观测计划

观测计划规定某个时段接收机与观测点的对应关系.拟定观测计划的基本思路是:用r台仪器进行观测，一个时段观测设计图中连接起来的r-1条基线,逐个时段就可以完成全部基线或全部测点的观测.如对于图1,用4台仪器进行观测,每个时段观测相互连接的3条基线,只要观测4个时段就能完成全部12条基线的测量.第1时段可将仪器安置在1、2、3、4上,观测1-2、2-3、3-4 3条基线;第2时段可将仪器安置在10、4、5、6上，观测10-4、4-5、5-6 3条基线;第3时段可将仪器安置在6、9、8、10上，观测6-9、9-8、8-10 3条基线;第4时段可将仪器安置在6、7、1、8上，观测6-7、7-1、1-8 3条基线.

按照上述观测计划,既不会漏掉一条基线,也不会多测一条基线,还可有多种可选方案.如对于图1，第1时段还可将仪器安置在7、1、2、8上，观测7-1、1-8、1-2 3条基线;第2时段将仪器安置在2、3、4、10上，观测2-3、3-4、4-10 3条基线;第3时段将仪器安置在4、5、6、7上，观测4-5、5-6、6-7 3条基线;第4时段将仪器安置在6、9、8、10上，观测6-9、9-8、8-10 3条基线.具体设计时应该按照一定的标准选择最优的方案.

5 GNSS控制网的自动设计与实现

GNSS观测方案自动生成的基本思想是:首先根据GNSS测点近似坐标及其所围成的多边形进行三角形剖分[14-15],同时生成测点、测线、三角形及三角网之间的拓扑(包括邻接、包含)关系表;然后,按文中所述公式计算时段数c、总基线数J0、独立基线数J1、必要基线数J2、多余基线数J3、平均边数、两类多边形的边数和个数,依照三角形的邻接关系表,构建异步环网,生成异步环、独立基线、测点之间的拓扑关系表;最后,遍历搜索所有独立基线,根据拓扑邻接和包含关系,按照迁站总数最小的原则,完成测站调度方案的自动生成,从而实现GNSS网观测方案的精准设计.程序界面如图2所示，

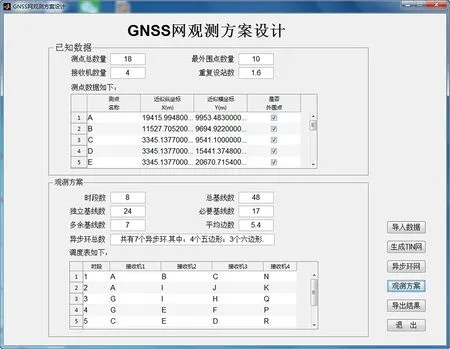
图2 程序界面

以一个由18个点组成的GNSS控制网为例演示程序的运行过程.程序运行之前先在选定图上指定外围多边形,然后按照图3的格式在EXECL中输入测点总数量、接收机数量、最外围点数量、重复设站数、测点名、X坐标、Y坐标,并指明是否为边界点,输入后将文件命名保存.

图3 EXECL格式的数据

程序的执行过程如下：

第1步 在程序界面上点击“导入数据”,找到保存的EXECL文件并打开,数据会自动导入到程序中,并显示在程序界面的“已知数据”栏中.

第2步 点击“生成TIN网”,出现如图4所示的TIN网图.

图4 TIN网图

第3步 点击“异步环网”,生成设计好的网图,如图5所示.

图5 GNSS网图

第4步 点击“观测方案”,生成观测方案图,如图6所示,其中1,2,…,8表示时段数;同时,观测方案的数据统计以及调度表显示在程序界面的“观测方案”栏中,如图2所示.

图6 观测方案图

第5步 点击“导出结果”,可将观测计划(调度表)输出到EXECL表格中,如表1所示.表1中的测点和图6中的基线完全对应,如第7时段,表1中显示的接收机安置在K、M、N、O上,对应于图6中的3条基线是N-K、N-M、N-O.另外,从表1中可以看出,设站次数最多的是C、E,为3次,最少的是B、D、F、H、J、L,为1次,其余点上都设站2次,站数分配均匀,这说明程序优化设计比较合理.

表1 观测计划表

6 结语

1)由于独立基线数、闭合环数、外围多边形的基线数、闭合环的平均基线数之间存在确定的数学关系,因此,闭合环的平均基线数是可以计算的.

2)如果平均基线数是小数,则多边形的基线数只有两个值：一个是平均基线数向下取整;另一个是平均基线数向上取整.可以保证图形的美观和精度的平均.

3)直接根据设计好的图形逐条基线而不是逐个测点进行观测，依此拟定的观测计划目标明确、思路清晰,不会多测,也不会漏测,可行可靠.

4)按照本文的设计思想易于实现计算机的自动优化设计.