基于球谐函数的单花形生成及应用

金 耀, 李文轩

(浙江理工大学 信息学院,杭州 310018)

面料花形可为纺织品注入艺术附加值,有力提高纺织品的市场竞争力,是纺织品设计的重要组成要素[1]。传统的人工设计方式通常需要设计师在短时间内挖掘创作灵感,对设计师要求较高,较难适应当前“快节奏”的个性化市场需求。而利用计算机数字化技术生成花形图案(又称数字艺术图形)能够有效地解决传统设计所存在的问题。数字艺术图形能高效地生成大量富于变化且具艺术美感的花形,因此可为传统纺织品花形设计提供大量新型素材,并为设计师带来创作灵感,使其显著地提高设计效率,同时能够有效地避免版权问题。

数字艺术图形类型较多,如分形图形[2-3]、动力系统图形[4-5]、均匀随机网图形[6-7]、准规则斑图[8-10]等。这些图形虽生成原理各异,但均具有复杂多变、艺术美感丰富等特点。分形图形是一种具有自相似性、结构复杂的数字艺术图形,按其生成方法又可分为L-系统图形、IFS(迭代函数系统)图形、复动力系统图形等,且其研究工作一直充满活力[2-3]。动力系统图形基于离散动力系统理论,是对混沌动力系统迭代过程进行可视化的结果[11]。均匀随机网与准规则斑图均基于弱混沌理论生成[8-9],前者是对磁场粒子运动轨迹可视化的结果,其骨架结构变化丰富,具有精细线条排列的效果;后者对哈密顿算子进行平滑操作,其具有规则性、对称性、造型丰富、时尚型突出等特点。

不同类型的数字艺术图形风格迥异,在众多领域有着广泛应用,尤其在纺织品设计中受到人们的青睐。一般而言,数字艺术图形作为素材往往需要从中提取单花形,并通过二次设计进行设计应用。张聿等[6]基于均匀随机网图形进行丝绸纹织设计。丁玲聪等[12]基于广义牛顿迭代图形,以松果造型为灵感源设计丝巾纹样。贾凤霞等[13]通过叠加多项式生成Julia集图形,将其应用于设计科幻星空为灵感源的服装纹样。洪潘等[14]根据纺织品图案流行趋势,使用准规则斑图设计具有英伦格子和苏格兰格等传统风格的格子图案。潘寒菲[1]同样基于准规则斑图并借鉴不同的灵感源设计丝巾图案。然而,这些方法在进行二次设计时存在如下问题:分形或均匀随机网图形虽能生成具有独立结构的单花形,但需要大量的调参筛选出合适的图形;准规则斑图或动力系统所生成的图形往往铺满整个图像空间,需借助软件经繁杂的交互式分割提取单花形。

为高效地生成单花形图案,本文提出一种基于球谐函数的数字艺术图形生成方法。该方法利用等高线分割法将具有“星型”特点的球谐函数曲面投影成二维单花形图形,使之能直接作为设计的基本元素,避免繁琐的元素提取步骤;同时,该方法变化形式更加容易控制,能够根据特定系数控制图形的对称性。最后,本文结合铺砌结构探索了该图形在纺织品图案与产品设计中的应用。

1 基于球谐函数的花形生成

1.1 球谐函数模型

球谐函数为定义在球面上的拉普拉斯算子的特征函数,作为一组标准正交基,通常用于逼近复杂的球面函数[15]。球谐函数在三维空间表示为一个封闭的“星形”曲面,其中心为球面函数的球心,且由中心沿着任意方向的射线与该曲面有且仅有一个交点。Paul Bourke[16]提出了一种显式球谐函数,该函数具有8个参数,其表达式如下:

r=sin(m0φ)m1+cos(m2φ)m3+sin(m4θ)m5+cos(m6θ)m7

(1)

式中:r为曲面上的点到球心(通常设为坐标原点)的距离,φ为曲面上的点的位矢与z轴的夹角(0≤φ≤π),θ为曲面上的点的位矢在xOy平面的投影与x轴的夹角(0≤θ≤2π);mi(0≤i≤7)为球谐函数的系数,决定曲面的形状,一般取为非负整数。为方便论述,本文称mi(0≤i≤3)为φ相关系数,mi(4≤i≤7)为θ相关系数。

图1为不同系数所生成的球谐函数曲面,可见其外形美观,形态多样。

图1 三种球谐函数曲面Fig.1 Three spherical harmonic surfaces

1.2 单花形生成方法

借鉴准规则斑图生成方法[10],本文对球谐函数曲面进行等高线分割以生成二维图形。具体讲,根据曲面的高度值z(仅考虑正数部分)划分等高线,对位于相邻等高线的点赋予相同的颜色,从而确保图形颜色呈块状分布,避免“散点”问题。

由于该球谐函数难以求出高度z的解析解,若采用数值解法则将增加计算量,降低图形的生成效率,因此本文不采用逐像素的方法(依次计算每个像素对应的高度z),而是使用垂直投影的方法生成图形。首先将曲面离散化,对经纬向的角度(θ,φ)进行均匀采样,并将其剖分成四边形网格;然后根据四边形面片上其中一个顶点的高度z划分等高线族,并依次对所有四边形面片进行平面着色;最后使用垂直投影法将所有四边形面片投影至xOy平面,最终生成二维图形。其具体步骤如下:

1) 设置基本参数:φ相关系数,θ相关系数,以及球坐标系下离散曲面的角度分辨率a×b,其中a、b分别为经纬方向角度采样分辨率。

2) 计算采样角度步长du、dv,公式如下:

(2)

式中:du为球坐标系下θ轴方向的步长;dv为球坐标系下φ轴方向的步长。

3) 设置等高线数目、各等高线之间的距离及所对应的颜色。为使图形颜色分布尽量均匀,根据高度z对曲面进行等距划分。通常可根据均分高度值,使各等高线间的距离相同。等距划分的公式如下:

c=|(z/d)modq|

(3)

式中:q为等高线数目;d为各等高线间的距离;z为曲面上一点的高度;c为等高线序号,向下取整可以将相近的等高线融合,使图形颜色呈块状分布。

通过式(3)可以计算出等高线序号,等高线序号一致的点将被赋予相同的颜色。

4) 定义球坐标系下曲面上点的序号(nθ,nφ),其中nθ=0,1,2,…,a-1;nφ=0,1,2,…,b-1。依次遍历网格曲面顶点的编号,每次遍历时先根据下式计算出(nθ,nφ)对应的(θ,φ):

(4)

根据式(1)依次计算出(θ,φ),(θ+du,φ),(θ,φ+dv),(θ+du,φ+dv)对应的r,然后根据下式计算出相应的四个三维直角坐标:

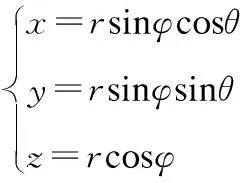
(5)

若(θ,φ)对应的曲面高度z为正,则将(θ,φ)对应的曲面高度z代入式(3),并计算得到等高线序号,用等高线序号对应的颜色和四个三维直角坐标进行四边形面片的绘制,其中着色方式使用平面着色。遍历结束,完成三维网格曲面的绘制。

5) 将三维曲面垂直投影到xOy平面,生成相应的二维图形。图2展示了球谐函数的三维曲面和对应的二维投影。

图2 球谐函数图案Fig.2 Graphs generated by spherical harmonic function

1.3 对称花形构造

对称是设计美学的一个重要原则,传递平衡稳定之美感。球谐函数在特定条件下表现出多种对称性,主要包括反射对称和旋转对称。由于图形生成方法沿z轴进行垂直投影,球谐函数曲面最终被投影到xOy平面,θ为曲面上的点的位矢在xOy平面的投影与x轴的夹角,因此图形的对称性与θ有关。

为使图形具有关于x轴的反射对称性,则高度函数z需满足式(6),即将式(5)中的高度函数z代入式(6),然后化简得到式(7)。根据三角函数的周期性可知,无论m6、m7取何值(定义域范围内),式(7)中的cos项必定满足等式,因此仅需考虑sin项。当m5为偶数时,式(7)中的sin项满足等式,此时图形具有关于x轴的反射对称性。

z(φ,θ)=z(φ,2π-θ)

(6)

(7)

为使图形具有关于y轴的反射对称性,则需满足式(8),即将式(5)中的高度函数z代入式(8),再化简得到式(9)。同样,根据三角函数的周期性,当m4为奇数或m5为偶数时,式(9)中的sin项满足等式;当m6为偶数或m7为偶数时,式(9)中的cos项满足等式;当两项同时满足要求,则图形具有关于y轴的反射对称性。

z(φ,θ)=z(φ,π-θ)

(8)

(9)

此外,为使图形具有k-旋转对称性,则需满足下式:

(10)

由于对称性与φ无关,本文仅考虑式(1)中θ对应的两个三角函数项,则有如下两种情况。

1) 当该两个三角函数项均被启用时(指数均不为0),两者周期应为倍数关系,且较大者应为T,公式如下:

(11)

式中:Tsin为sin项的周期;Tcos为cos项的周期。

由式(1)可知,影响Tsin的系数是m4、m5,影响Tcos的系数是m6、m7。其中m4、m6为角频率,m5、m7为指数。当指数为偶数时,三角函数周期为奇指数的1/2。因此可以得到sin项和cos项的周期计算公式为:

(12)

2) 当该两个三角函数项仅有一项被启用时,则无需考虑两者的倍数关系,启用项的周期应等于T,仍可根据式(12)计算得到。

综上,若要使图形具有k-旋转对称性,需首先根据式(10)计算得到T,然后选择三角函数项的启用数量(2或1)。若启用数量为1,则需根据式(12)设置启用项系数使其周期等于T;若启用数量为2,则需根据式(12)设置θ相关系数,使式(11)成立。

2 实验与讨论

本文使用C++编程语言并借助OpenGL图形库(使用其提供的内置函数实现垂直投影)进行实验,分别探讨了等高线分割方式和球谐函数系数对生成图形的影响,并基于实验探索了控制图形变化形式的规律。

2.1 等高线分割方式

为探讨等高线分割方式对生成图形的影响,本文分别设置了不同等高线分割数目、不同等高线间距及不同的色彩主题,生成相应的图形。

图3展示了等高线分割数目对图形的影响结果,其中d=0.16,mi={1,5,5,0,2,6,2,2}。由图3可见,等高线数目增加后,图形颜色数增加,并从内向外循环交替,而图形内部色彩纹理和外部轮廓均保持不变。这是由于等高线间距离未随等高线数目增加而增加,各颜色所占区域面积未受影响。

图3 不同等高线分割数目所生成的花形图案Fig.3 Flower-like patterns generated from different partitionnumbers of the contour line

图4展示了等高线间距离对图形的影响结果,其中q=3,{mi}={1,5,5,0,2,6,2,1}。由图4可见,等高线间距较小时,色彩层次较多,图形纹理感较强;随着等高线间距离增加,同种颜色所占区域的面积增大,图形色彩层次减少,纹理感减弱。这是由于等高线间距离增大,融合的相近等高线数量增多,使得同种颜色所占区域的面积增大,从而使得色彩层次变少。

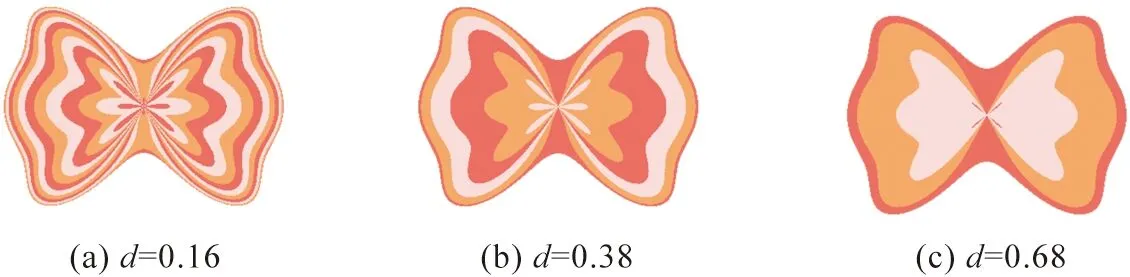
图4 不同划分距离的球谐函数花形图案Fig.4 Spherical harmonic flower-like patterns withdifferent partition distances

图5展示了色彩主题对图形的影响结果,其中q=3,d=0.35,{mi}={12,0,5,0,3,6,3,0}。调整各等高线序号所对应的颜色,即可改变图形的色彩主题。图5所选色彩主题依次为“复古”“温暖”“寒冷”“光明”“黑暗”“自然”“童话”“清新”“狂野”。由图5可见,色彩主题的改变不会影响图形纹理和外部轮廓形状,但能使图形风格有较大的变化。使用者能够根据自己喜好进行色彩搭配,并将图形应用于不同主题风格的设计中。

图5 不同色彩主题的球谐函数花形图案Fig.5 Spherical harmonic flower-like patterns with different color themes

综上不难发现,等高线分割方式的改变仅会影响图形的内部样式,包括颜色数、色彩纹理、色彩主题等,并不会影响图形的外部轮廓,因为外部形状由球谐函数的参数决定。

2.2 球谐函数系数

为探讨球谐函数系数对生成图形的影响,本文设置不同的θ和φ相关系数,利用同一等高线分割法生成图形,其中q=3,d=0.33,并选用同一组配色。

θ相关系数由m4、m5、m6、m7组成,其中m4、m5控制θ对应的sin项,m6、m7控制θ对应的cos项;m4、m6为角频率,m5、m7为指数。首先讨论启用一项三角函数对图形的影响,将m1、m3、m5置0,避免其他三角函数项的干扰。图6展示了m6、m7系数对球谐函数图形的影响,小标题的8个整数对应球谐函数的8个生成系数mi(i=0,1,2,…,7)。由图6可见,图形呈现花瓣状且具有旋转对称性,当m7为奇数时,图形“花瓣数”即旋转倍数k等于m6,各“花瓣”具有相同的纹理结构和外部轮廓,如图6(a～c)所示。当m7为偶数时,图形“花瓣数”等于m6的两倍,如图6(d～f)所示。这是由于仅启用一项三角函数时,无论系数取何值(定义域范围内),旋转对称性的构造条件必满足,式(10)中T等于启用项的周期。因此,根据式(12)计算启用项的周期,当m7为奇数时,旋转倍数k等于m6;当m7为偶数时,旋转倍数k等于m6的两倍。

图6 m6、m7系数控制的球谐函数花形图案(m5=0)Fig.6 Spherical harmonic flower-like patterns controlledby parameters m6 and m7 (m5=0)

接下来讨论启用θ系数对应的两项三角函数对图形的影响,m5不置0。图7展示了m4、m5、m6、m7系数对图形的影响。由图7可见,当启用两项三角函数时,图形整体外部轮廓较图6产生更复杂的变化,这是由于不同θ系数的选取会满足不同的对称性条件。由于图7(a)的球谐函数中m4为奇数,m6为偶数,因此图形关于y轴反射对称。图7(c)由于m5为偶数,因此图形关于x轴反射对称。同一图形可能呈现多种对称性,如图7(b)同时具有旋转对称性,以及关于x轴和y轴的反射对称性,这是由于其θ相关系数同时满足三类对称性的构造条件。

图7 m4、m5、m6、m7系数控制的球谐函数花形图案(m5≠0)Fig.7 Spherical harmonic flower-like patterns controlled byparameters m4, m5, m6 and m7 (m5≠0)

不难发现,θ相关系数的改变会使图形整体外部轮廓产生变化,不同系数搭配会使图形具有不同的对称性。图形内部色彩纹理保持不变,图形颜色过渡自然,几何结构鲜明,符合人的自然审美。

φ相关系数由m0、m1、m2、m3组成,其中m0、m2为角频率,m1、m3为指数项。图8展示了m0、m1、m2、m3系数对生成图形的影响结果。图8(a)为未启用φ相关系数的图形,图8(b～c)为启用φ相关系数的图形。相较于图8(a),图8(b～c)内部色彩纹理发生改变,但图形外部轮廓并没有发生变化,这是由于φ相关系数与对称性无关。

图8 m0、m1、m2、m3系数控制的球谐函数花形图案Fig.8 Spherical harmonic flower-like patterns controlledby parameters m0, m1, m2 and m3

上述实验结果表明,θ相关系数影响图形的外部轮廓,φ相关系数影响图形的色彩纹理,当启用θ相关系数中一项三角函数时,图形必定具有旋转对称性,且对称倍数容易控制。当启用θ相关系数中两项三角函数时,不同的系数搭配会使图形具有不同的对称性,由此可以生成外部轮廓更加复杂多样的图形。当启用φ相关系数或改变等高线分割方式时,可以改变图形的内部样式,使图形种类更加丰富。

因此,在进行调参时可首先设置θ相关系数控制外部轮廓的变化,然后设置φ相关系数和等高线分割方式,控制图形内部样式的变化。图9展示了利用该思路生成的部分图形。由图9可见,该方法能够较为方便地生成“变化丰富”且具有自然美感的数字艺术图形。

图9 球谐函数花形图案Fig.9 Spherical harmonics flower-like patterns

3 设计应用

由上述计算机实验可知,基于球谐函数的花形图案具有如下特点:花形独立成形,形状既似自然花瓣状,又具独特的抽象风格。为此,本文将这类花形应用于纺织品图案及产品设计实践中。总体设计过程概括为:挖掘灵感源,定位消费者人群,生成与主题风格相符的球谐函数图形,进行二次设计,最后模拟仿真。

3.1 灵感源

雪花是冬天特有的晶体产物,其独特的蓝白配色给人带来清澈透明的感受,能够凸显纯净的气息。本文以此为灵感源,借鉴雪花配色,利用球谐函数方法生成相似风格的图形,并在此基础上进行纺织品图案的设计。

3.2 消费者人群定位

雪花风格主题的消费者人群以18～25岁的女大学生及新入职女性为主,该目标人群的典型特点是充满青春活力,内心纯洁,对未来生活充满向往,善于接受新事物。

3.3 球谐函数图形生成

本文选用浅蓝、深蓝、白三色生成球谐函数图形,其中q=3,d=0.33,生成图形如图10所示。图10(a)为“三花瓣”样式,其基本结构为正三角形;图10(b)呈现“六花瓣”样式,其基本结构为正六边形。

图10 雪花风格的花形Fig.10 Patterns with snowflake styles

3.4 图案二次设计

传统的纺织品图案设计多采用二方连续或四方连续的方式对花形进行空间布局构图,其纹样节奏均匀,韵律统一。铺砌是指通过铺砌块无缝且不交叉地覆盖平面的方法,可以分为周期性铺砌和非周期性铺砌,其中周期性铺砌是指支持在两个非平行方向上的平移对称变换方法,其在视觉上表现为一种无线重复可延伸的图案,且在纺织品设计中得到了应用[17]。为丰富构图形式,本文将铺砌应用于图案布局,结合所生成的球谐函数花形图案进行二次设计。阿基米德铺砌是一种基本的周期性铺砌结构,其铺砌块为正多边形,例如正三角形、正四边形、正五边形等,图11(a)展示了由正三角形和正六边形构成的铺砌结构,图11(b)展示了由正八边形和正四边形组成的铺砌结构。

图11 阿基米德铺砌结构Fig.11 Structures of Archimedean tilings

由于生成的花形图案具有一定的几何结构,因此将图10(a)作为三角形铺砌块,图10(b)作为六边形铺砌块,并结合图11(b)所示的铺砌结构进行设计,得到如图12(a)所示的纺织品图案。进一步地,在图11(b)所示的铺砌结构的基础上,使用更多的球谐函数花形作为铺砌块并对图案结构进行微调,得到如图12(b～c)所示的纺织品图案。相较于如图13所示的二方连续结构,使用铺砌理论设计的纺织品图案具有更丰富的表现形式,局部变化多样,又不失整体谐和。

图12 结合铺砌的雪花纺织品图案Fig.12 Textile patterns designed with snowflake patterns

图13 二方连续下的雪花纺织品图案Fig.13 Textile patterns designed with spherical harmonicpatterns (two-dimension series)

3.5 产品效果图模拟

结合铺砌方法所设计球谐函数花形的纺织品图案疏密有致,图形层次清晰,并且铺砌结构的多样性使该类图案的构图变化丰富;同时,由于该类图案的基本元素由球谐函数模型生成,具有一定的对称性和相似性,使得该类图案具有协调统一之感;再者,该类图案的色彩风格由球谐函数图形决定,而球谐函数图形的色彩风格可以自由控制,能够产生不同的视觉效果。相较于其他纺织品图案,该类图案具有更多变化形式并能够保证图案整体的和谐统一,能够适用于不同风格的设计主题和不同类型的纺织品设计。

本文设计的具有雪花风格的图案便可应用于不同的纺织产品设计中,如丝巾、抱枕、地毯、窗帘等。为验证其可行性,本文使用Photoshop软件设计产品实物,并模拟产品图案的设计效果。图14分别展示了图12三个图案应用于丝巾、抱枕、地毯的设计效果。由图14可见,基于球谐函数所设计的图案应用于不同产品,其风格既有典雅明快、纯净通透的视觉效果又各有自身的特色。

图14 三种纺织品的模拟效果示意Fig.14 Design sketches of three textile products

本文方法可根据设计意图,利用图形的对称性条件选择合适的参数生成理想花形,具有较强的可控性;其次,由于其结构简单、独立成形的特点,使其无需进行元素提取而直接配上构图,即可生成纺织品图案,从而大大提高了设计效率。

4 结 语

本文提出了基于球谐函数的单花形数字艺术图形生成方法,并给出了不同对称性的图形构造条件。计算机实验表明,利用球谐函数方法生成的图形具有单花形特点,能直接作为设计的基本元素,且图形的变化形式容易控制。仿真实验进一步表明,该图形应用于纺织品图案与产品设计是可行的。未来将进一步针对基于球谐函数的花形生成方法,研究更为多样的图形控制方法及图形矢量化技术,从而为设计师进行二次设计提供更为便捷的手段。

《丝绸》官网下载

中国知网下载