随机波动率下障碍期权的Monte Carlo模拟定价
0 引言
Black-Scholes(BS)期权定价模型[1]以无风险利率、资产波动率是常数为假设基础,这一假设基础常常与实际市场价格不符。而随机波动模型,将波动率看成一个随机过程,可以更好地模拟实际市场的价格,应用较多的有Hull-White[2],Heston[3]等随机波动模型。郁瑞澜,商豪[4]用Heston随机波动模型讨论了沪深300ETF期权定价。梁艳[5]用了Hull-White随机波动模型对亚式期权进行模拟定价。
障碍期权(Barrier Options),指的是期权生效或失效取决于期权到期前是否达到障碍值。障碍期权由达到障碍值后的期权状态,可分为两种:敲出期权与敲入期权。敲出、敲入期权各可以分为四类,其名称和收益函数如表1所示。

表1 敲出、敲入期权的收益函数
张素梅[6]用有限差分法讨论了随机波动模型下的障碍期权定价。霍海峰等[7]在分数次布朗运动下探索了欧式障碍期权的定价。薛广明[8]研究了带跳随机波动率模型的美式障碍期权的定价。本文研究了随机波动模型下障碍期权[9]的定价,给出了股价波动率和标的资产的价格路径,用蒙特卡罗法(Monte Carlo)和对偶变量法[10]得出了下降敲出欧式看跌期权在不同条件下的期权价格,并利用对偶变量法,计算出了随机波动模型下下降敲出看涨期权的价格。
1 随机波动基本模型
在风险中性下,资产和波动率满足如下微分方程(1):

μ:股票期望收益率,σt:股票波动率与Bt是标准的Brownan运动,Hull-White随机波动模型下的各个参数如下:

本文的障碍期权定价,是在Hull-White随机波动模型下来研究的,则方程组(1)可简化为:

2 Monte Carlo模拟定价
2.1 Monte Carlo模拟的基本原理
大数定律和中心极限定理是Monte Carlo模拟的理论基础。模拟时,计算机多次重复抽取随机变量作为样本,当样本达到一定数量时,随机变量的均值就会接逐渐近于其期望值。

2.2 对偶变量法

2.3 蒙特卡罗模拟障碍期权定价的步骤
2.3.1 随机波动过程的模拟

2.3.2 股票价格路径的模拟
在风险中性条件下,方程组(2)中的标的资产可以写为

2.3.3 期权价格的模拟计算
欧式期权的股票价格终值为:

3 数值模拟结果与分析
3.1 蒙特卡罗法和对偶变量法的模拟结果比较
首先,分别用普通Monte Carlo法和对偶变量法比较下降敲出欧式看跌期权在不同的执行价格、交易时间下的期权价格[12],参数分别为S0=100,r=0.1,H=90,σ=0.3,模拟次数为5000次,时间离散步数为600。
由表2可以看出:①下降敲出看跌障碍期权价格随着K的增大而增大,随着T的增大而减小,当T=1/4时,不管是Monte Carlo法还是对偶变量法,K=105时的期权价格是之前的K=95和K=100时价格的好多倍,这种差距很明显,但是随着时间的增加,这种差距略有减小;②对偶变量法与普通Monte Carlo法相比,模拟出来的结果更加精确,标准差更小些,但是在时间的运行上,对偶变量法的运行时间比蒙特卡罗法的略长一些,matlab运行时,蒙特卡罗法基本上5秒左右都能得出结果,对偶变量法一般需要6秒左右的时间。因此,为了使得数值更加精确一些,下面的随机波动模型的模拟过程选择对偶变量法。
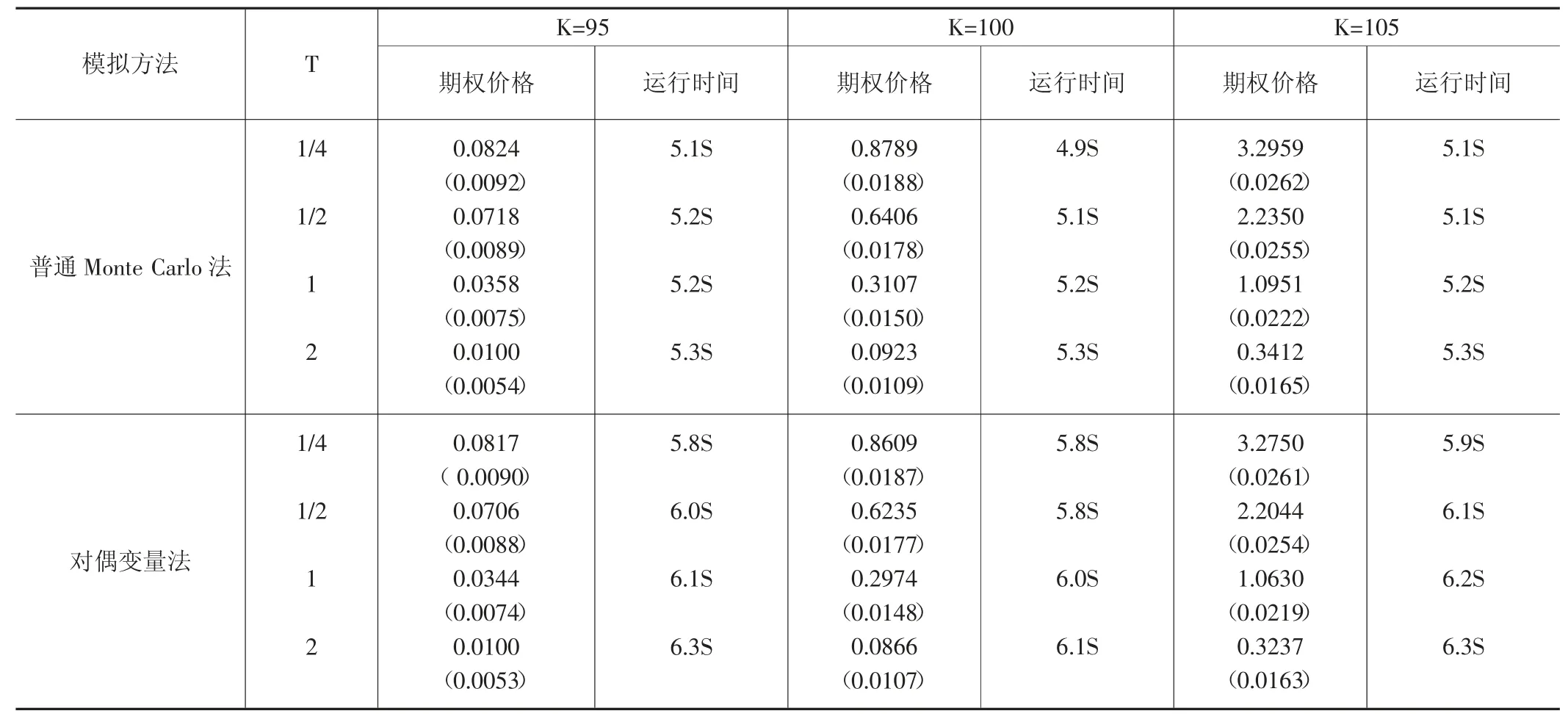
表2 蒙特卡罗法和对偶变量法比较下降敲出看跌期权
3.2 B-S模型和随机波动模型的模拟结果比较
其次,分别用B-S常波动模型和Hull-White随机波动模型(SV)来计算下降敲出欧式看涨期权的价格,参数分别取S0=100,μ=0,r=0.1,H=90,ρ=0,σ=0.1,Y(0)=0.08,模拟次数为1000次。
由表3可以看出:①下降敲出欧式看涨期权,随着执行价格K的增高,期权价格越来越低,随着时间T的增加,期权价格越来越高;②随机波动模型与常波动的B-S模型相比,随机波动模型模拟出来的期权价格比B-S模型的略低些,说明波动率为常数的时候,有可能高估了期权的实际价格。

表3 B-S模型和随机波动模型下降敲出欧式看涨期权价格比较
4 结论
本文研究了Hull-White随机波动模型,用Monte Carlo法对模型(3)给出具体的数值算法,利用matlab软件求出了下降敲出看跌期权的价格,并利用对偶变量法,通过matlab编程,模拟了随机波动模型下下降敲出看涨期权的价格,通过表2和表3的数值计算,验证了对偶变量法的准确性。

