局部冲坑对导管架刚度影响的模型试验

贺 瑞，宋俞良，郑金海

(1.河海大学海岸灾害及防护教育部重点实验室，江苏 南京 210098；2.河海大学港口海岸与近海工程学院，江苏 南京 210098)

目前冲坑对导管架基础刚度影响的研究较少，冲刷降低导管架基础的刚度，会引起海上风机自振频率下降，可能会导致共振，从而影响导管架风机的疲劳寿命。He等[28]通过严谨的半解析理论研究了冲坑对导管架基础静、动力特性的影响，考虑了桩-桩相互影响、冲坑-冲坑相互作用、桩-冲坑相互作用、砂土和黏土应力历史、冲坑真实形状、土体渗透性等多种因素的影响。但试验方面的研究目前仍未见报道，因此采用模型试验研究冲坑对海上风机导管架基础刚度的影响具有重要的工程意义与应用价值。

1 试验布置与有限元参数设置

本文模型试验在1.1 m×1.1 m×1 m土槽内进行，通过水平静载试验及振动特性测试研究风机正常运行工况下冲坑对导管架刚度及风机共振频率的影响，并通过有限元模拟验证试验规律。

1.1 模型参数及相似关系

海上风机正常运行状态下砂土几乎完全排水，同时考虑到砂土渗透性较强，因此采用干砂进行试验，砂土颗粒级配曲线见图1。砂土物理参数：粒径范围为0.1～0.4 mm，中值粒径为0.18 mm，最小干密度为1.254 g/cm3，最大干密度为1.653 g/cm3，摩擦角约为30°，相对密实度约为70%，孔隙比为0.77。试验通过砂雨法装置进行土体制备，控制土体密实度在70%左右。导管架模型参数见表1，试验布置如图2所示，图中S为冲坑深度，θ为冲坑坡度约为砂土天然休止角。本文使用无量纲参数S/D表示导管架基桩桩周冲坑最大深度与桩径的比值。模型参数与前人研究[2-3]对照见表2。

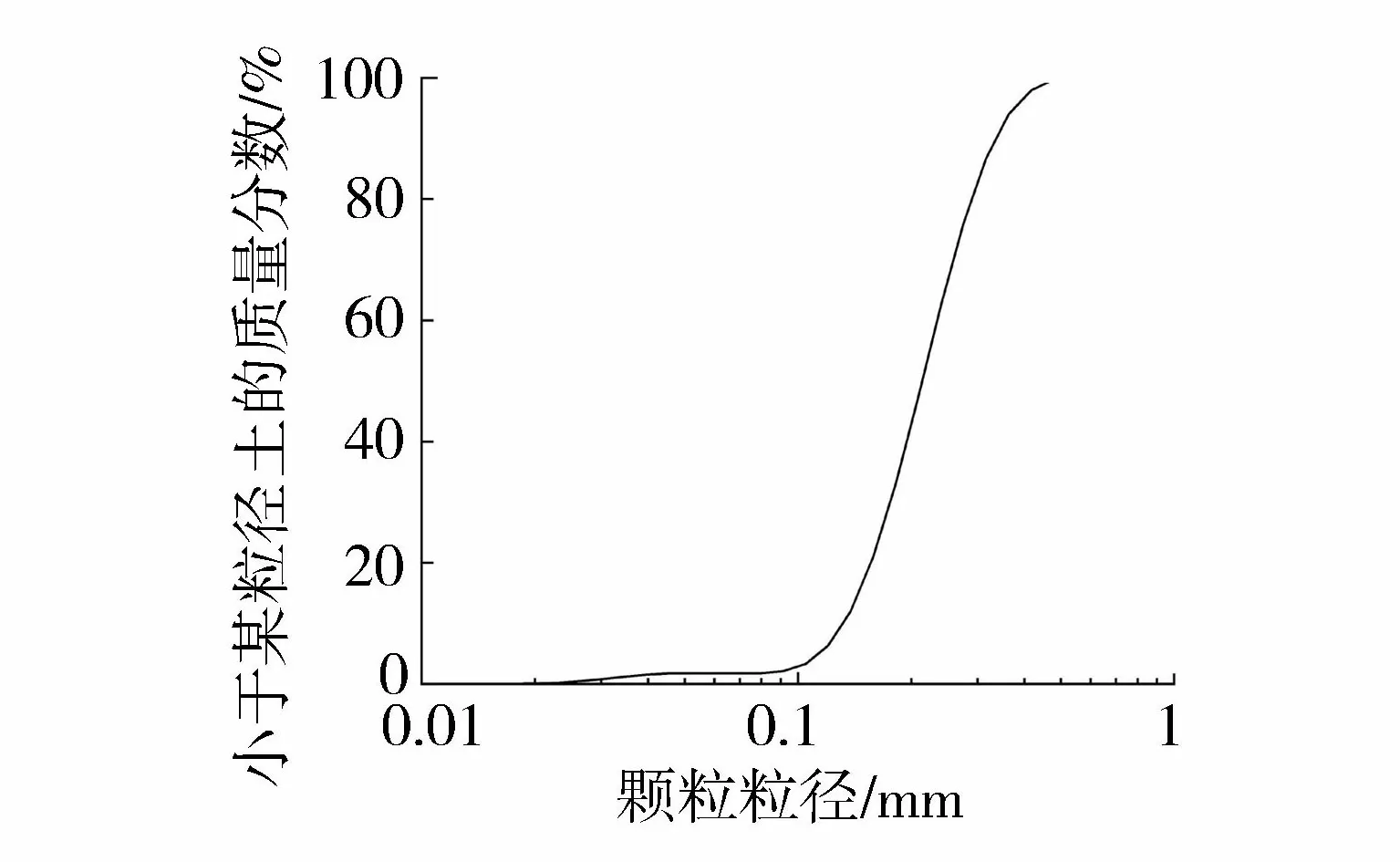
图1 土体颗粒级配曲线Fig.1 Soil particle gradation curve

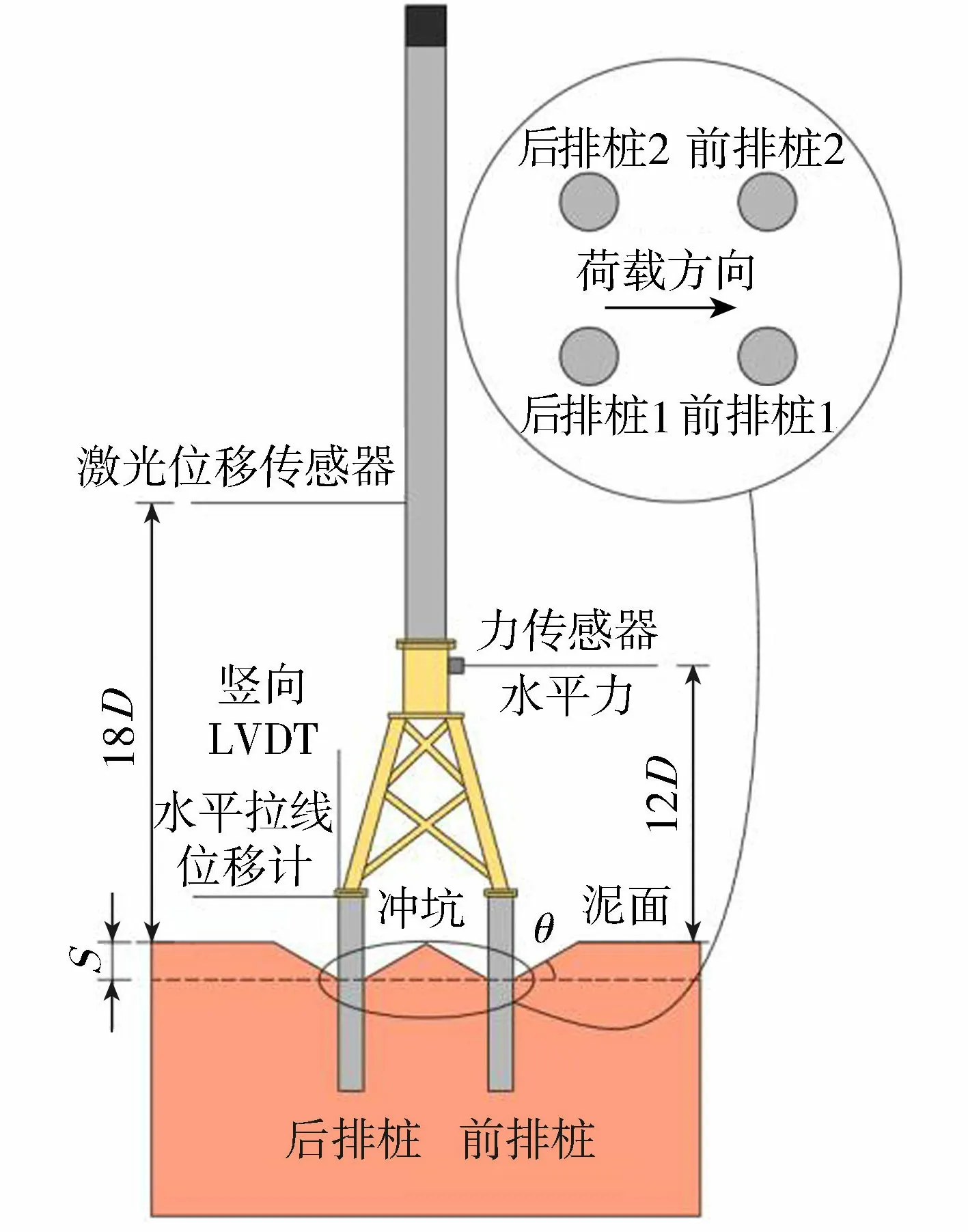
图2 试验布置示意图Fig.2 Schematic diagram of test layout

表1 导管架模型参数

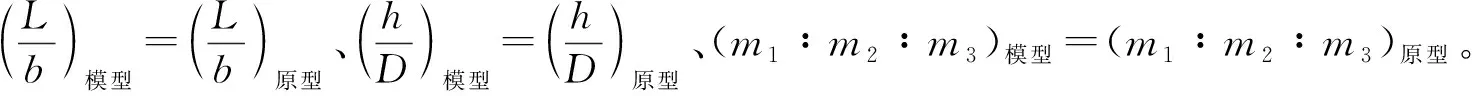
表2 本文模型试验与文献[2-3]参数对照

表3 模型相似关系取值

1.2 静载试验布置

静载试验中，使用预先放置桩的方法完成导管架模型的布置：先通过砂雨法将模型槽内砂土制备至距底面40 cm高度处，随后使用固定装置将4根基桩预先放置至指定位置，之后继续采用砂雨法制备土样至预定高度。土样制备完成后，通过刚性法兰盘完成导管架模型与基桩、塔筒与导管架模型的连接。模型安装完成后，考虑不同冲坑深度与坑面半径，在土槽中逐渐取出桩周土形成近圆锥形土坑以模拟实际冲刷过程中真实的局部冲坑。随后安装加载及测量装置进行水平静载试验。试验中通过水平滑轮提供水平静力，通过激光位移传感器测量塔架水平位移(泥面以上18D处)，在基桩桩顶设置竖向的直线位移传感器(LVDT)和水平向的拉线位移传感器(图2)。测量装置还包括测量桩身轴力及弯矩的应变片，在前后排2根桩各布置了测量弯曲应变的半桥桥路和测量轴向应变的全桥桥路。静载试验中设置了水平单向加载(S/D=0，1.5)和加卸载(S/D=0，1，1.5)的试验组次，重点研究了冲坑深度、荷载等级对导管架刚度的影响，具体试验组次参数见表4。

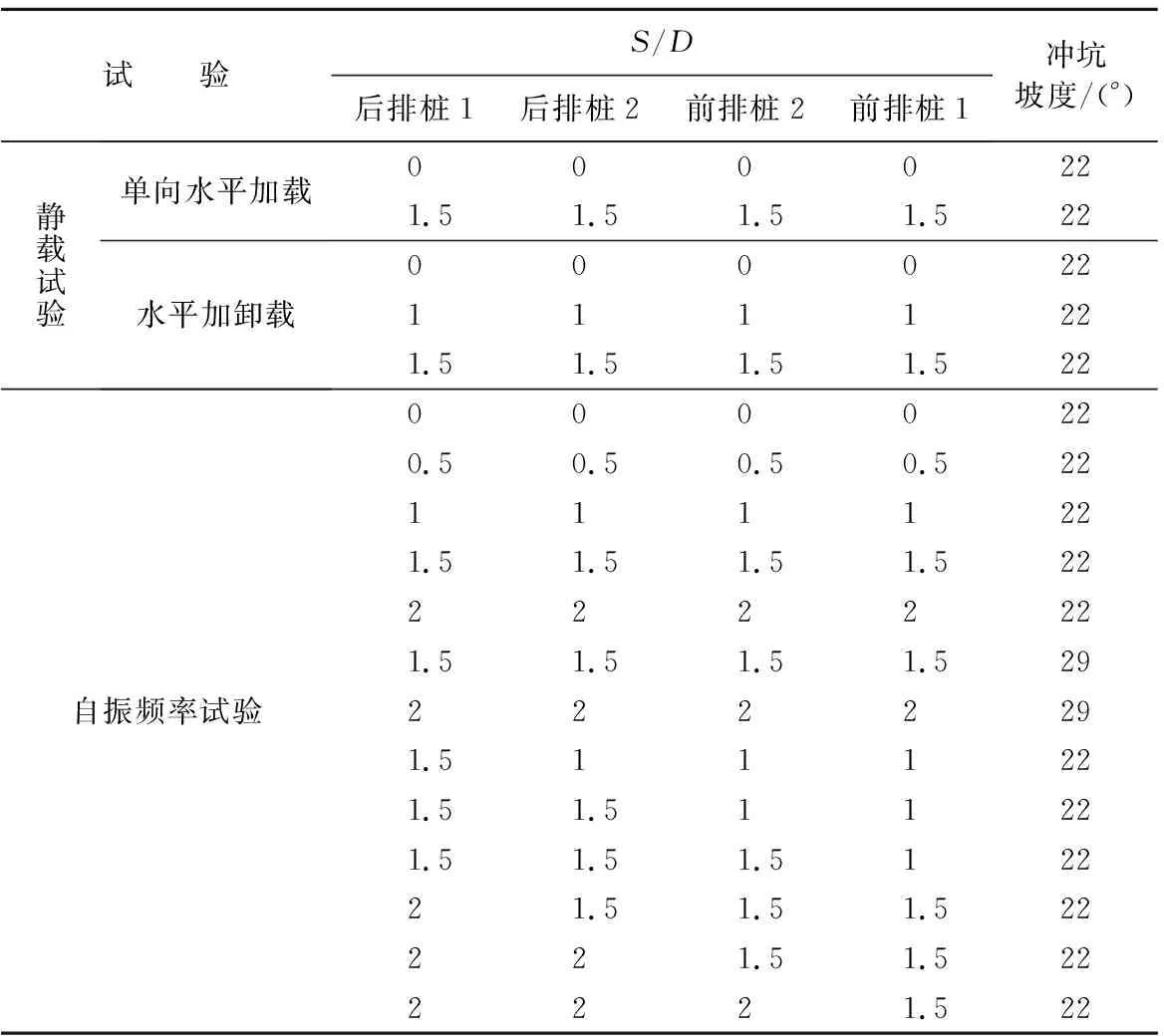
表4 试验组次参数

1.3 静载有限元模拟验证

本文主要以试验研究为主，有限元模拟仅用于验证试验规律。在有限元模型中，为简化计算，将土体视为均匀介质，土体本构模型采用摩尔-库伦理想弹塑性模型，土体内摩擦角使用低围压三轴试验结果设置为30°。由于试验中的桩基埋深较小，故通过共振柱试验研究极低围压时的砂土剪切模量随应变衰减曲线，利用共振柱试验(试验用土的相对密实度Dr=77%，试验围压为1 kPa)得到土样的剪切应变与剪切模量关系，利用Hardin-Drnevich模型[33-34](模型拟合参数γr=7.9×10-5、Gmax=5.4 MPa)拟合得到动剪切模量衰减曲线如图3所示，其中γ为土体应变。有限元模型尺寸和试验一致，基桩按照试验空心管桩尺寸使用实体单元进行建模，导管架与塔筒使用梁单元建模，连接板使用壳单元建模。基桩和导管架之间刚接，导管架和上部结构刚接。基桩弹性模量Ep=71 GPa，密度ρp=2 700 kg/cm3，泊松比νp=0.3，导管架和塔筒弹性模量Esteel=210 GPa，密度ρsteel=7 800 kg/cm3，泊松比νsteel=0.3。基桩和土体采用六面体八节点线性缩减积分单元。桩土接触面采用主-从面的面面接触算法，接触面属性采用摩尔-库伦罚函数，边界条件与试验条件一致，地基土的四周对平动自由度进行约束，土底面采用固定约束。在进行刚度分析前使用预应力场和自动平衡法进行地应力平衡。数值模型计算得到S/D=0时的塔架位移与单向加载试验与加卸载试验数据对比如图4所示，有限元计算与试验数据较为一致。

图3 土体剪切模量衰减曲线Fig.3 Decay curve of soil shear modulus

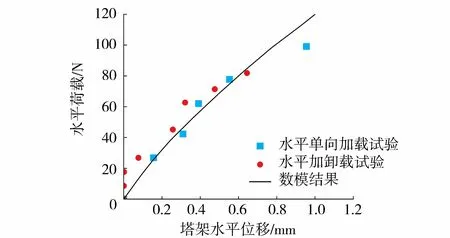
图4 有限元结果验证Fig.4 Validation of finite element result

1.4 导管架自振频率试验布置

力锤试验是获得频响函数的一种非常流行的方法[35]，通过安装在力传感器的锤头提供一定频率范围的激励，根据力传感器测得的锤击力和结构不同位置处的加速度传感器测得的加速度得到结构的频响函数，进而可以得到结构的共振频率等振动特性参数。本文在砂雨法制备好土体之后，通过调整冲坑的深度和冲坑半径，实现了不同冲坑坡度、不同冲坑深度的变化，通过力锤试验研究了冲坑深度(S/D= 0、0.5、1、1.5、2)、冲坑坡度(θ=22°、29°)对导管架共振频率的影响。由于实际冲刷过程后排桩先产生冲刷，前排桩后出现冲刷，前后排桩桩周冲坑出现时间顺序不同，因此考虑导管架由S/D= 1到S/D= 2的冲刷过程中模拟按图2中后排桩1、后排桩2、前排桩2、前排桩1逐渐增加冲坑深度的顺序进行自振频率试验，研究冲刷顺序对导管架共振频率的影响，具体试验组次参数设置见表4。

2 结 果 分 析

2.1 静载结果分析

图5为无冲刷时水平单向荷载增大时的基桩水平和竖向位移，可以看出，后排桩和前排桩水平位移基本一致；随荷载增大，后排桩竖向位移比前排桩更大。

图5 无冲刷时荷载-基桩位移Fig.5 Load-pile displacement without scour

图6对比了冲刷前后的的荷载-结构位移 (前后排桩水平位移一致，故选取前排桩水平位移代表基桩水平位移)，可以看出，当局部冲坑深度为1.5D时，荷载较小时有冲坑情况与无冲坑情况位移差异不明显，基桩水平、竖向位移变化较小，冲刷对水平、竖向初始刚度影响不明显；当荷载较大时，冲坑对导管架水平静刚度的影响不容忽视，冲刷对基桩的竖向刚度影响较大。

图6 冲刷前后荷载-结构位移Fig.6 Load-structural displacement before and after scour

加卸载试验塔架水平位移如图7所示。加卸载下导管架刚度受冲坑深度影响变化规律与单调加载情况类似：当荷载较小时，冲坑影响很小；但冲坑的影响随着荷载增加而变大；卸载刚度值大于相同位移处的加载刚度；此外，卸载后塔架有部分不能恢复的残余位移，残余位移随冲坑深度的增加而增加。

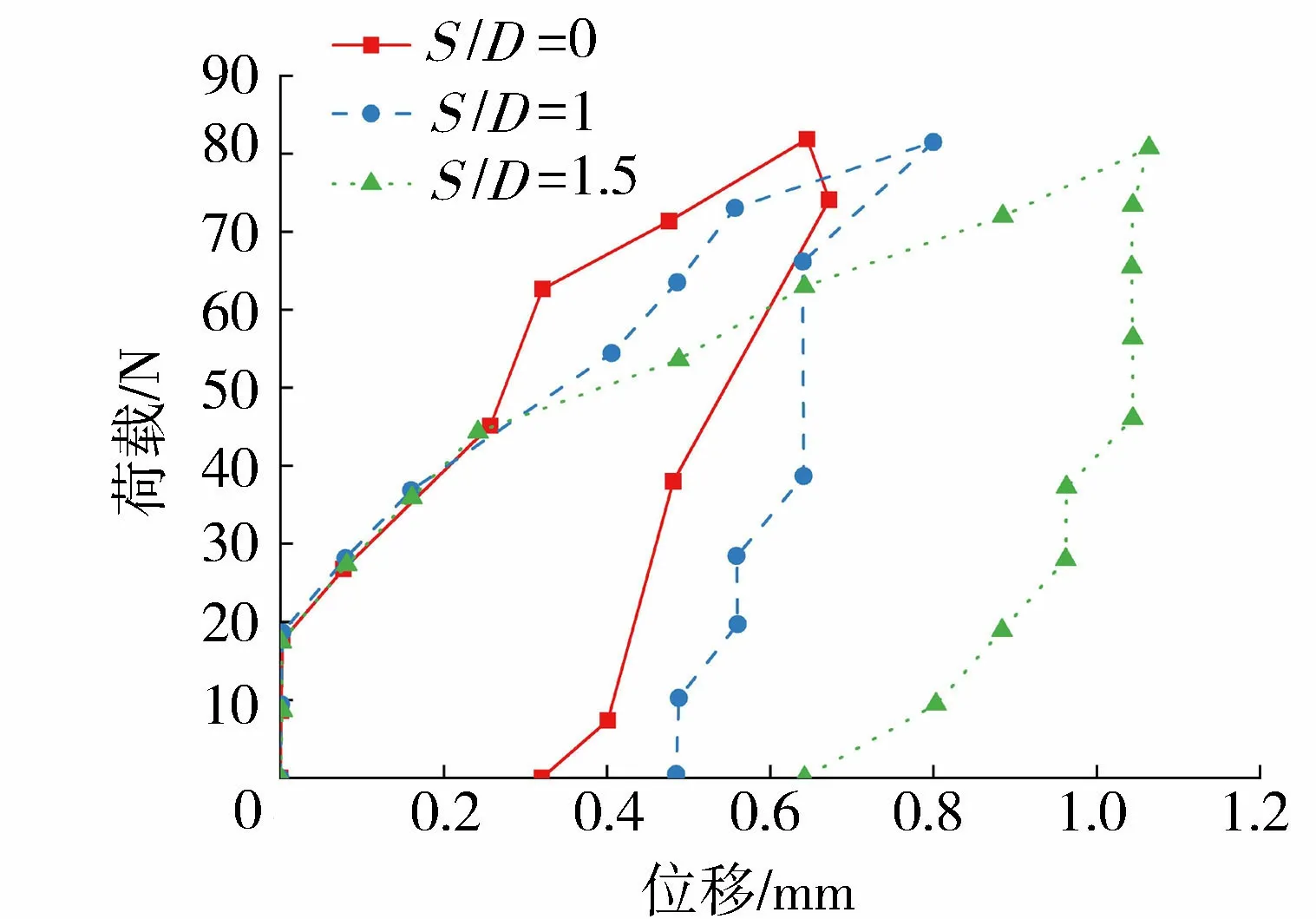
图7 加卸载试验塔架水平位移Fig.7 Horizontal displacement of tower in loading and unloading test

图8给出了无冲刷时不同荷载下前排桩桩身弯矩，图9给出了54 N水平荷载下不同冲坑深度时的前排桩桩身弯矩。整体来看，桩身弯矩都非常小，并非桩基承受的主要荷载。图10给出了无冲刷时前后排桩弯矩随荷载变化的比值，可以看出水平荷载较小时，前排桩所承担弯矩略大于后排桩，当荷载增大时，前后排桩弯矩比值趋近于1。由图8可看出当荷载增大时，前排桩桩身弯矩增大，荷载从27 N增大至54 N，桩身最大弯矩约增大为原来的2倍；当荷载值从54 N增大至71 N，荷载值增加31%，弯矩最大值增大20%，此时桩身弯矩随荷载增大出现非线性变化。由图9可看出，桩身弯矩随冲坑深度增加而增大。图11为冲坑对桩基弯矩影响的数值模拟结果，能够看出桩身弯矩随冲坑变化的规律与试验一致；但由于数值模型对土体真实剪切模量进行了简化，导致试验和数值模型计算结果稍有差异。由图9、图11可看出，当荷载相同时，冲坑深度增加，前后排桩桩身最大弯矩点下移。

图8 无冲刷时不同荷载下前排桩桩身弯矩Fig.8 Bending moment of front pile under different loads when scour depth is 0D

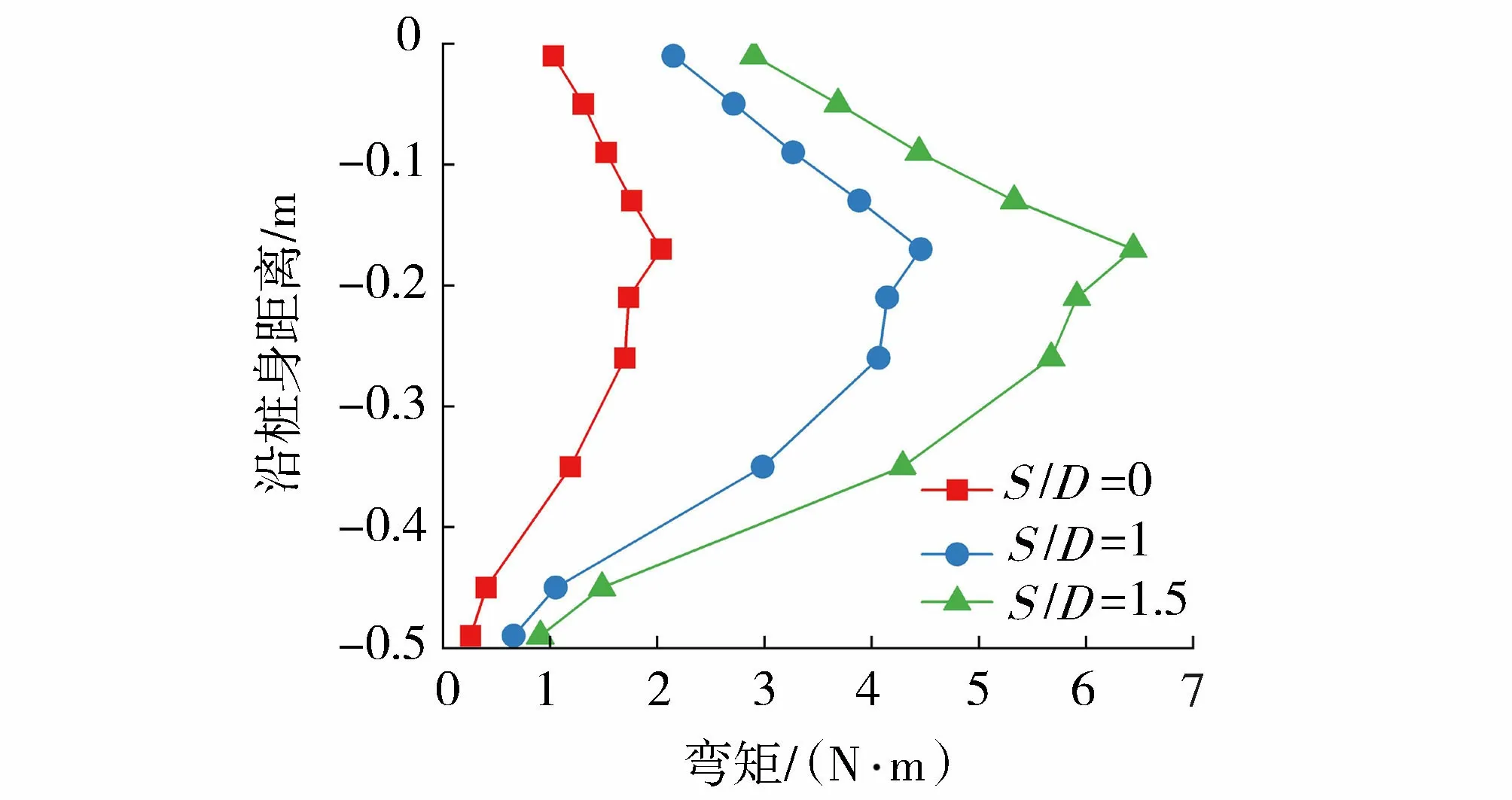
图9 54 N水平荷载下不同冲坑深度前排桩桩身弯矩Fig.9 Bending moment of front pile under different scour depths when the lateral load is 54 N

图10 无冲刷时前后排桩弯矩比值Fig.10 Bending moment ratio of front and back piles when the depth of scour is 0D

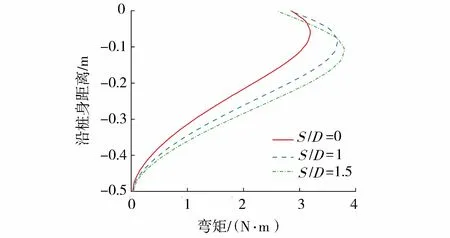
图11 54 N水平荷载下前排桩弯矩数值模拟结果Fig.11 Bending moment of the front pile in FEM when the lateral load is 54 N

在试验中通过桩身布置应变片测得轴向应变，由于应变片在水平荷载加载前进行了清零，该应变实际反映导管架基桩受水平荷载时的轴力增量。通过数值模型计算得到仅受自重时的基桩初始轴力(图12)，与水平加载过程中桩身轴力增量(图13)叠加，得到桩基最终的轴力分布(图14(a)、图14(b))。由图14(a)可知，随荷载增大，前排桩受下压力，从而轴力增大；后排桩受上拔力，从而轴力减小。沿桩身从泥面到桩底由最大轴力逐渐变为0；当荷载一定时，前排桩在自重压力叠加上部水平荷载产生的下压力，导致整体轴力增加；而对于后排桩，自重压力逐渐被水平荷载产生的上拔力抵消，整体轴力逐渐减小，并逐渐从压力转变为拉力。由图14(b)看出，当水平荷载较小时，冲坑对轴力分布影响并不明显。图14(c)为冲坑对桩基轴力影响的数值模拟结果，整体规律与试验类似。

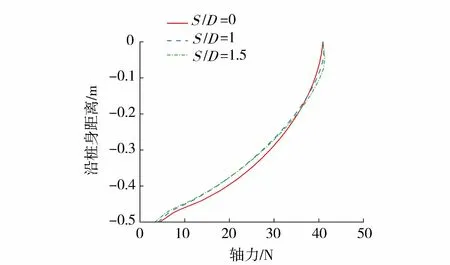
图12 桩身初始轴力Fig.12 Initial axial force of the pile

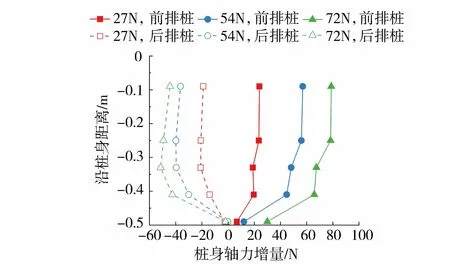
图13 桩身轴力增量Fig.13 Historical axial force increment

图14 不同情况下的桩身轴力Fig.14 Axial force of pile under different conditions

2.2 导管架自振频率试验结果分析

图15给出了塔顶测得共振频率随冲坑深度增加的示意图，图中α为傅里叶变化后桩基加速度的频率分布与共振频率的比值，能够更好地反映冲坑深度对共振频率的影响。可以看出当冲坑深度小于1D时，塔顶测得共振频率变化较小，当冲坑深度到1D时，导管架共振频率变化有轻微减小，直至导管架基桩出现1.5D深度冲坑，即后排桩冲坑深度到1.5D，导管架自振频率减小较为明显，塔顶处所得的共振频率在基桩冲坑深度达到1.5D时变化较为明显且下降较大，当冲坑深度为1.5D时，共振频率下降约3.2%；冲坑深度为2D时，共振频率下降约6.3%，这可以为海上风机运行过程中对基础冲刷深度监测提供帮助。

图15 冲坑深度对共振频率的影响Fig.15 Effect of scour depth on resonant frequency

海上风机运行期间波流荷载的作用导致导管架上游桩先出现较深冲坑，下游桩冲坑深度的增加滞后，这可能会影响导管架动力特性。因此通过试验模拟冲坑出现顺序对导管架共振频率的影响，由于冲坑深度大于1D时导管架共振频率有较大变化，故选定冲坑从1D发展到2D的过程作为研究范围。由图16可知(图中[abcd]表示后排桩1、后排桩2、前排桩2、前排桩1的冲坑深度与桩径的比值)，当冲坑深度为1D时，只要任一根基桩冲坑深度再增加，导管架共振频率即会出现较为明显的变化。

图16 冲坑出现顺序对共振频率的影响Fig.16 Effect of scour-hole occurrence order on resonance frequency

在实际冲刷过程中的桩基附近的冲坑形态较为复杂，但多近似为圆锥形，因此试验中针对S/D=1和S/D=1.5的2种冲坑深度选取2种不同坡度(29°和22°)的冲坑进行研究，图17给出了2种冲坑深度下不同冲坑坡度的结构共振频率，可以看出局部冲坑坡度对共振频率的影响并不明显。

图17 冲坑坡度对共振频率的影响Fig.17 Influence of slope angle of scour holes on resonance frequency

3 结 论

a.局部冲坑会降低导管架基础水平静刚度，当荷载水平较低时，1.5D深度以内冲坑对导管架基础整体刚度降低不明显；但冲坑的影响随荷载水平的增加而不断加大。

b.局部冲坑对导管架轴力的影响与对刚度的影响类似：1.5D深度以内冲坑在荷载水平较低时影响不明显，但影响随着荷载的增加而更加显著。

c.当冲坑深度达到1D时，导管架风机共振频率才发生可监测的下降；此时，只要任一基桩中再出现更深的冲坑，风机共振频率就会出现较明显下降；当局部冲坑深度为1.5D时，风机共振频率下降约3.2%；冲坑深度增加为2D时，风机共振频率下降约6.3%。

d.当局部冲坑为圆锥形时，保持冲坑深度不变，冲坑坡度对导管架风机共振频率的影响较小。