求多重多元复合函数偏导数的一般公式
◎马 悦 傅 勤
(江苏省苏州市苏州科技大学数学科学学院,江苏 苏州 215009)
一、引 言
多元函数微分学是高等数学和数学分析课程中的重要内容,其中的复合函数微分法主要讨论了复合函数的可微性、偏导数与全微分在研究复合函数的一般求导法则时,教材中运用了链式法则的求导方法但是在计算较复杂的复合函数时,简单地运用链式法则会使问题的解决变得烦琐文后的参考文献给出了多元函数求偏导数的一般公式,并没有给出求多重多元复合函数偏导数的一般公式为了解决此类问题,本文将从推导求二重复合函数偏导数的一般公式出发,研究求三重多元复合函数偏导数的一般公式,并进一步研究求多重任意元复合函数偏导数的一般公式
二、求二重、三重多元复合函数偏导数的一般公式
(一)文后参考文献中的已有公式
若(,…,)在点(,…,)可微,而=(,…,),=1,2,…,在点(,…,) 具有关于(=1,2,…,)的偏导数,则复合函数
((,…,),(,…,),…,(,…,))
关于自变量的偏导数是
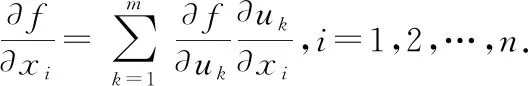
我们注意到:上述方法中每个函数的变量个数是相同的那么能否将此公式推广到更为一般的形式,即考虑到每个函数的变量个数不相同的情况呢?
文后的参考文献[3]~[7]提出了运用叉树表示元函数偏导数关系的树型法则,使得相应的计算过程可简化为:遍历各枝(子),最后到叶;兄弟用加,下辈用乘这个方法对之后研究多重多元复合函数的偏导数有很大的启发相应地运用三元树型法则计算三重复合函数偏导数的过程如下所示
函数是关于函数,,的复合函数,函数,,是分别关于自变量,,的函数,写出表达式如下:
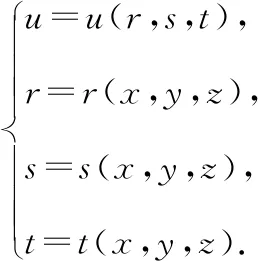

当天夜里秦川将她占有,或者说当天夜里她将秦川占有,她认为后者或许更恰当一些。她不是随便的女人,她无比保守,可是见到秦川,她就想将自己交付出去。她不是淫荡的女人,她无比清纯,可是见到赤裸的秦川,她甚至想跪下去亲吻秦川的脚趾。那几天里,她认为自己是世界上最合格的充气娃娃。

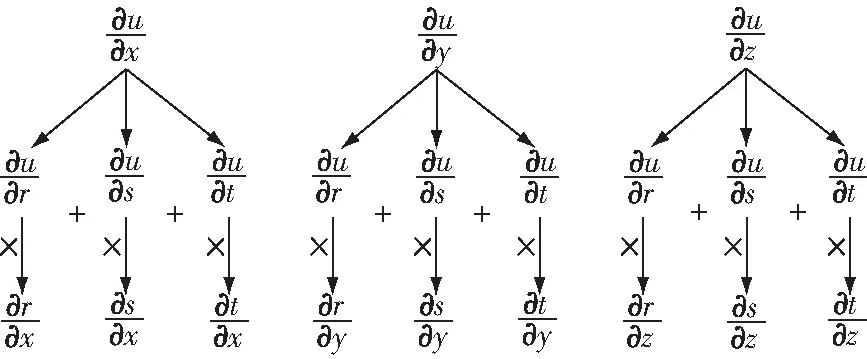
我们注意到:这些文献对树型法则的相关研究为多重多元复合函数偏导数的计算提供了很好的方法,但并没有给出求多重多元复合函数偏导数的一般公式本文将针对求多重任意元函数偏导数的一般公式进行更深入的研究
(二)求二重多元复合函数偏导数的一般公式
1若=(,…,)在点(,…,)可微,=(,…,),=1,2,…,,=1,2,…,在点(,…,)具有关于(=1,2,…,)的偏导数,则复合函数
((,…,),(,…,),…,(,…,))
关于自变量的偏导数是
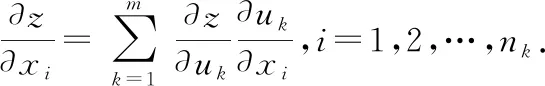
由定理条件可知

①
其中,,…,,,,…,,,,…,为当Δ,Δ,…,Δ趋于零时的无穷小又由=(,…,)在点(,…,)可微,所以

②
其中,,…,为当Δ,Δ,…,Δ趋于零时的无穷小将①代入②,可得
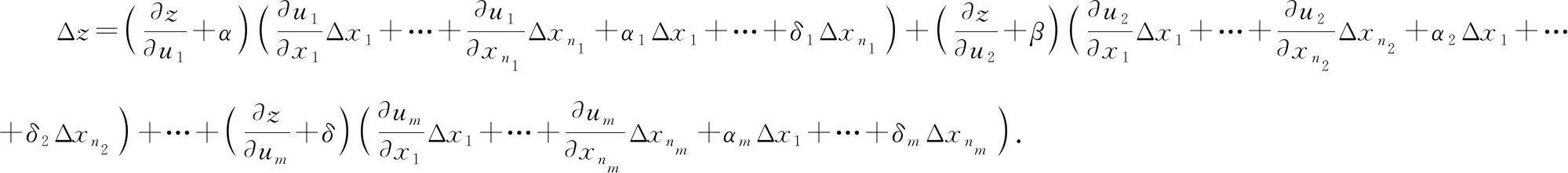

其中,
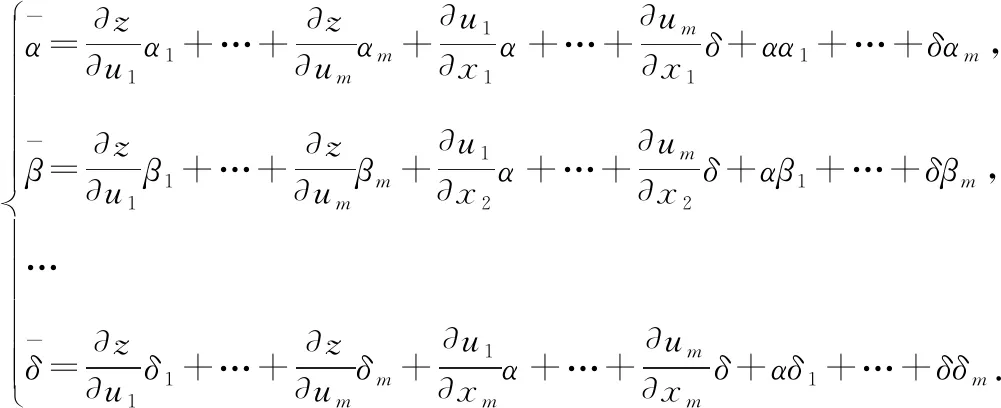
由此可以得到关于自变量的偏导数:
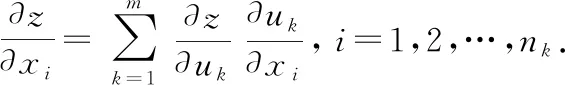
(三)求三重多元复合函数偏导数的一般公式

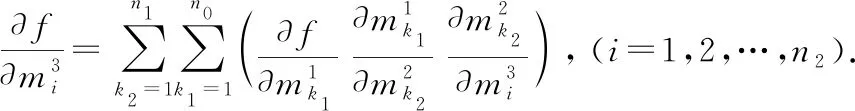
由定理条件可知
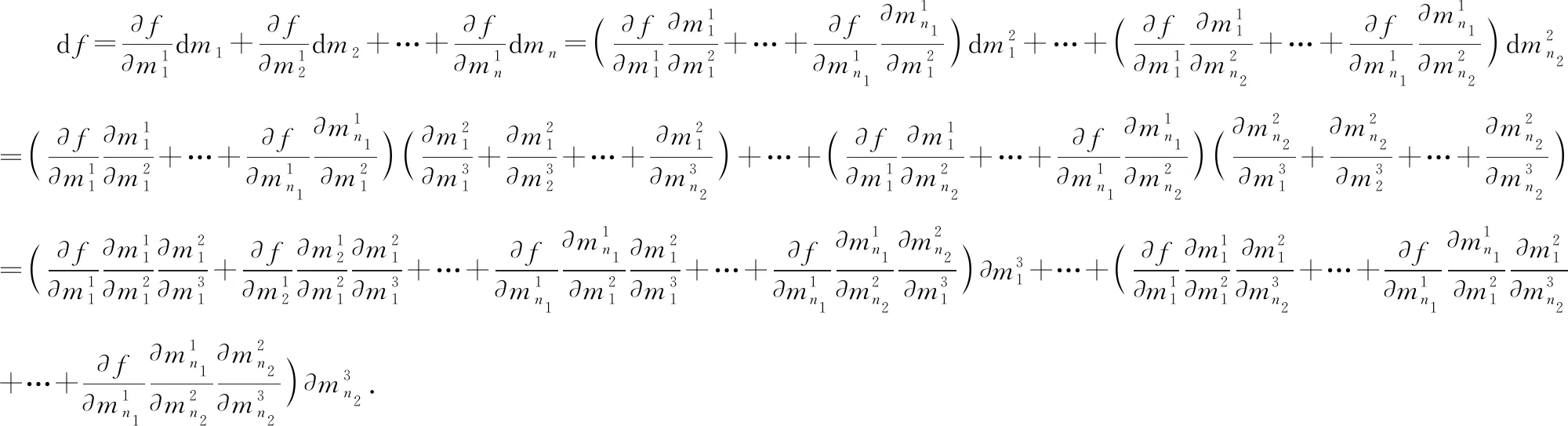

三、求多重多元复合函数偏导数的一般公式

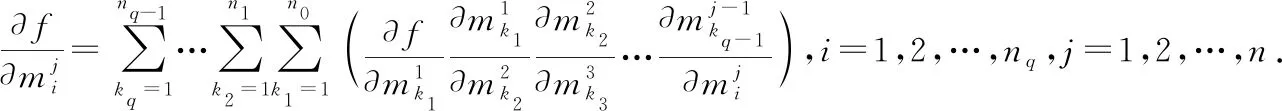
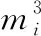
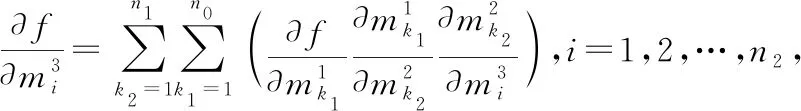
即结论成立
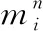


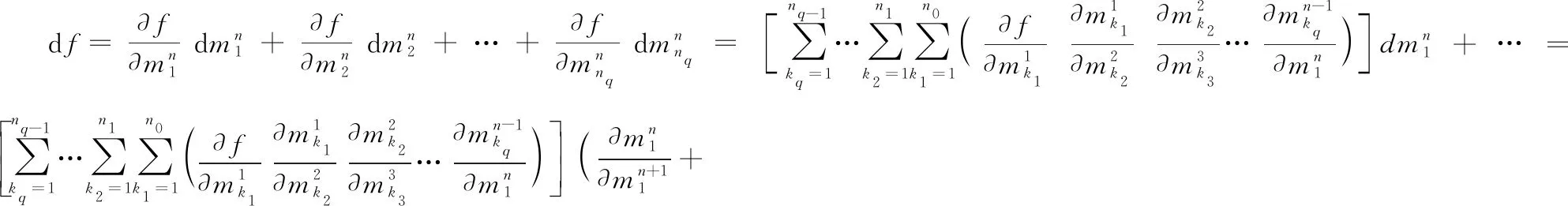
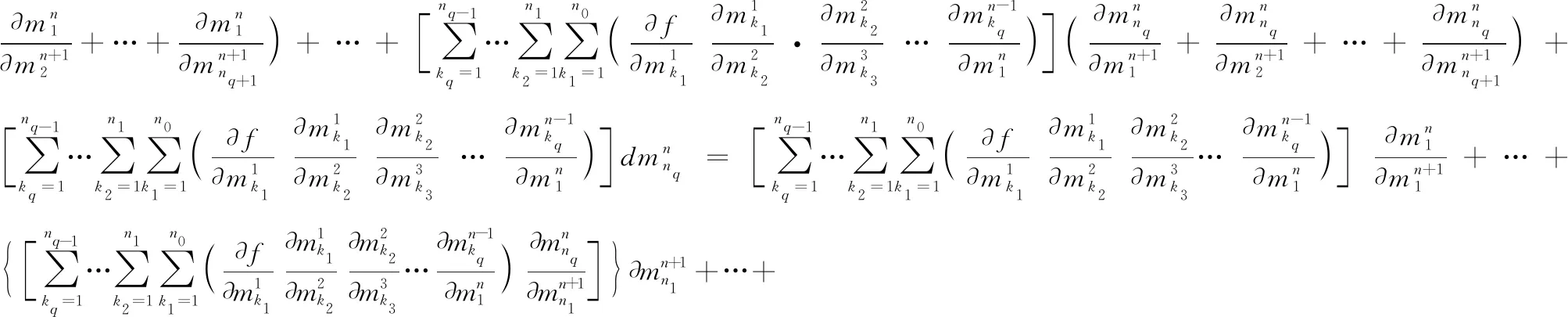
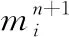
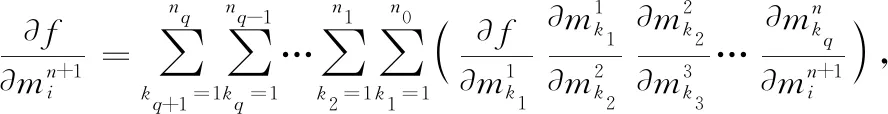
=1,2,…,+1
因此,对于+1重(为任意自然数)元复合函数,结论也成立证毕
四、结 语
本文从教材上已有的二重复合函数求偏导数的计算方法入手,尝试运用树型法则对多元多重函数进行偏导数的求解,通过研究得出求三重多元复合函数偏导数的一般公式,然后利用数学归纳法进一步推导出了求多重多元复合函数偏导数的一般公式

