数理统计课程中Cranmer-Rao不等式的教学案例设计

陶 红，徐耀坤，何章鸣，侯臣平

（国防科技大学 a.文理学院；b.电子科学学院，湖南 长沙 410073）

引言

数理统计是统计学的一个重要分支，在自然科学、工程技术、管理科学和人文社会科学等领域得到了越来越广泛的应用。很多高校的本科和研究生数学类与统计类专业均开设数理统计类课程。传统的数理统计教学着重于定义与公式的讲解与证明，这种讲授方法虽然能够准确传达课程知识，但在激发学生学习兴趣、培养数理统计思想、提升科研创新能力这些方面存在明显的不足。为了提升学生的学习兴趣，很多高校都在尝试采用案例教学法来提升数理统计课程的教学质量。已有的教学实践表明，在数理统计课程中引入案例教学模式，能够有效帮助学生加深对理论知识的理解和提升解决实际问题的能力。案例教学法的推广需要丰富的案例资源作为支撑。然而，目前我国高校数理统计课程的案例教学中，案例资源还比较匮乏。大多数案例内容陈旧，与当前社会的发展态势联系不够紧密，从而限制了案例教学法的作用。由此可见，数理统计教学案例建设的必要性与紧迫性。本文针对数理统计课程中Cramer-Rao不等式的教学目标和教学重点，结合相关领域前沿研究成果，从单分子定位超分辨成像和锂电池荷电状态估计两个实际应用中，凝练了两个Cramer-Rao不等式的教学案例，加强课程内容与实际问题的有效结合。

一、Cramer-Rao不等式的基本理论

在案例教学开始，首先对案例涉及的基本概念进行详细剖析。Cramer-Rao不等式的内涵是：对于Cramer-Rao正则族的可估参数，其无偏估计的协方差阵存在下界。这个下界被称为Cramer-Rao下界，由样本容量、Fisher信息和可估参数的导数确定。Cramer-Rao不等式的应用十分广泛，可应用于雷达运动目标检测、卫星定位系统、超精密测量和量子成像等科学研究和工程实践中的参数估计精度分析，对于提升实际应用中的参数估计性能具有重要作用。由于Cramer-Rao不等式在理论研究和工程实践中的重要地位，Cramer-Rao不等式一直是数理统计课程中的教学重点。

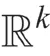
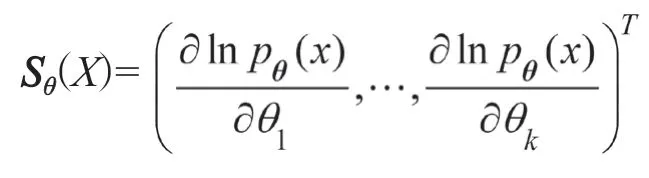
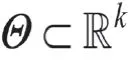
现有教材通常直接给出Fisher信息的定义与存在条件，然后再给出Cramer-Rao不等式的具体内容与证明。教师在教学的时候如果仅仅局限于教材，不结合实际应用进行适当延伸与拓展，那么学生对此部分内容的学习将停留于“背公式”的层面，不能深入理解Cramer-Rao不等式的应用途径。因此，需要发挥数理统计作为一门应用性极强的学科的特点，积极进行案例建设，扩大案例式教学法在数理统计教学中的应用范围，从而提升教学质量。事实上，Cramer-Rao不等式作为参数估计中误差分析的有力工具，已经在相关学科中得到广泛应用，结合基本理论，让我们分析以下案例。

二、Cramer-Rao不等式的案例设计

实际的教学案例设计中，要考虑学生对案例背后知识背景的掌握程度。笔者结合学生的已学课程，通过查阅相关学科的前沿研究成果，分别从单分子定位超分辨成像和锂电池荷电状态估计两个实际应用中凝练了两个Cramer-Rao不等式的教学案例，学习过“大学物理”基本课程的学生均可理解案例中的基本背景。两个不同的案例中，既有诺贝尔奖工作中的科学问题，又有贴近实际生活的工程问题，现予以分享。

案例1 基于单分子定位的显微成像技术（Single-Molecule Localization Microscopy,SMLM）获得2014年获得诺贝尔化学奖。SMLM的工作原理可以概括为“闪烁”“定位”与“重建”，即多次循环采集被稀疏激活的荧光分子，再利用单分子定位算法给出荧光分子精准的空间定位信息，最后将每一帧的定位点合成为一张超分辨图像。单分子定位算法的精度分析是成像分辨率分析中的一个基本且重要的问题。事实上，单分子定位就是对单分子的坐标进行估计。若获得了单分子坐标的无偏估计量，则此估计量的定位精度定义为其标准差。

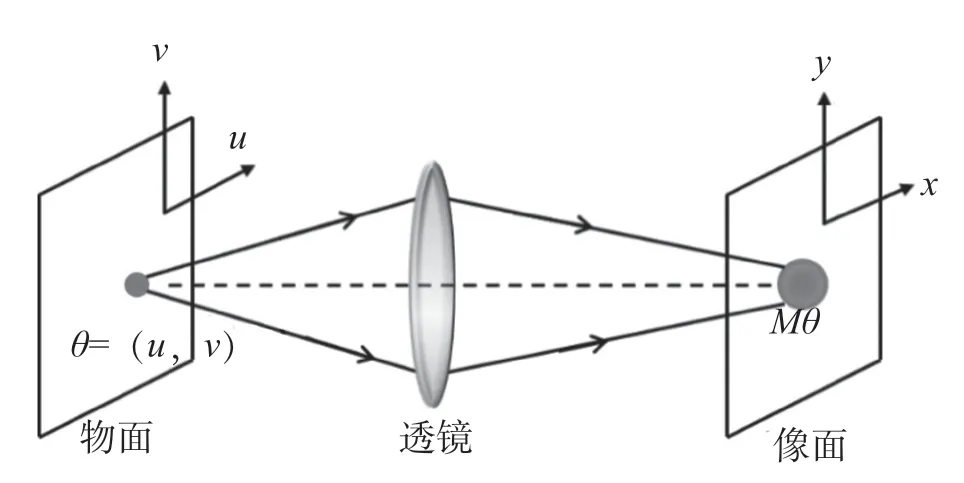
图1 单分子成像系统

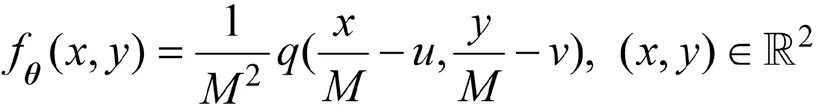
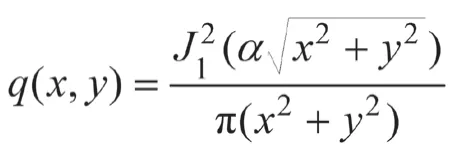
若采集到个光子，由此个光子的坐标构造出的的模平方可积的无偏估计为，且已知

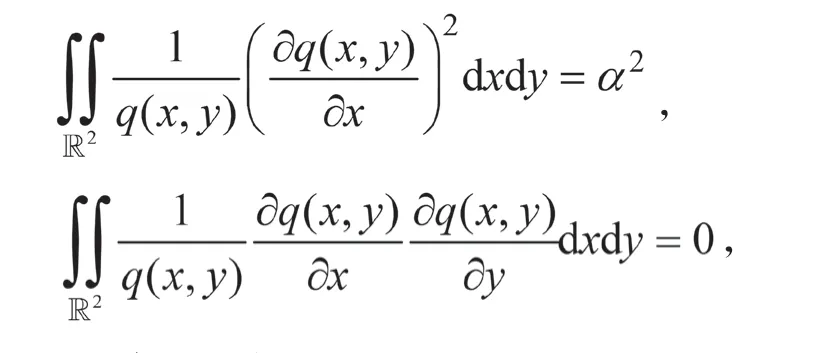
试求的方差下界。

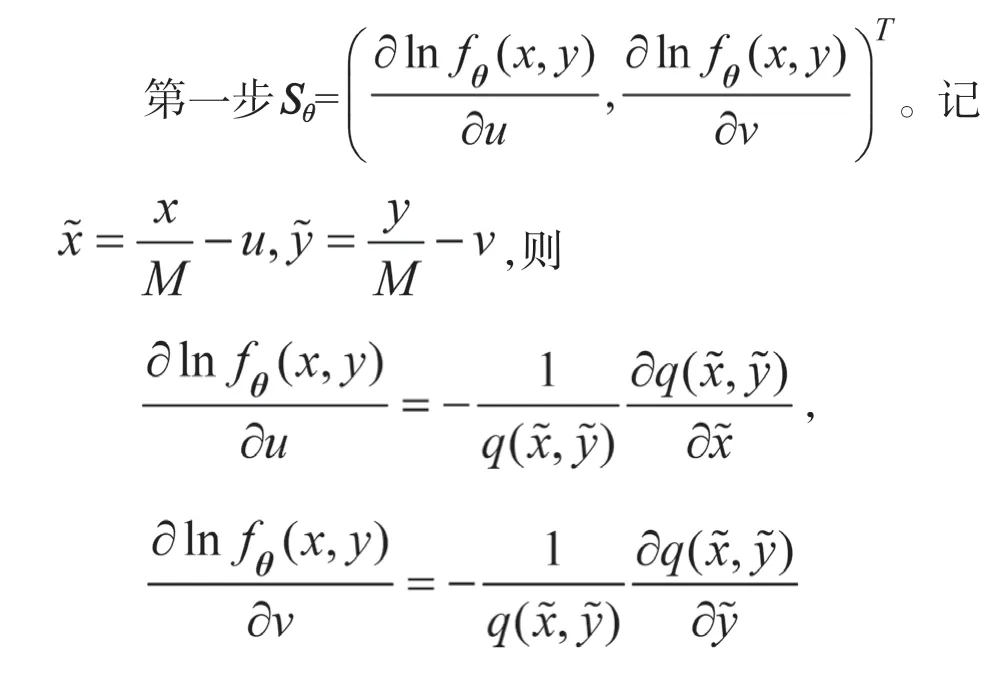
第二步，计算（）。

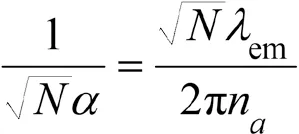
案例2 锂电池因其能量密度高、循环寿命长等优点迅速发展为新一代储能电源。准确估计电池当前工作状态，对于提高储能系统的安全性、可靠性和可用性具有重要作用。假设锂电池内部具有图2所示的RC等效电路模型。

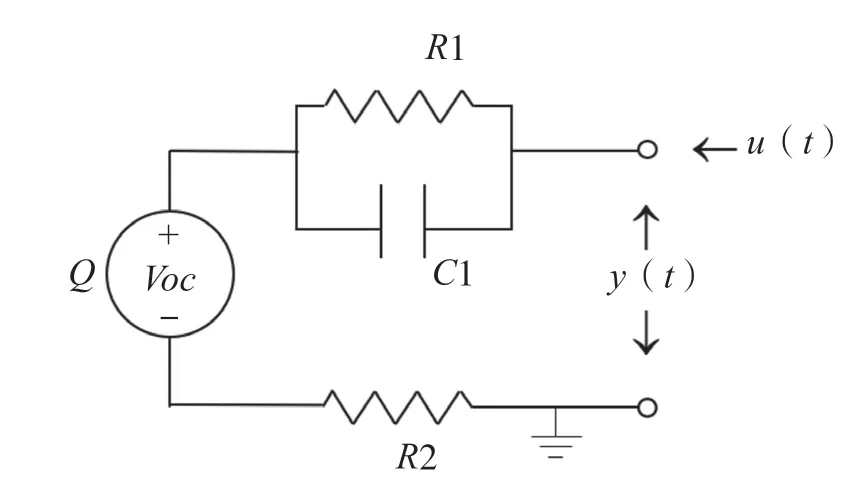
图2 锂电池内部RC等效电路图

此等效电路的工作原理为

其中表示电池的荷电状态（SOC），和分别表示电池的极化内阻和极化电容，表示平行电容器的电荷量，表示电池电量，表示电池欧姆内阻，表示输入电流，表示可直接测量的电池端口电压，OCV（）表示开路电压与SOC间的非线性关系并且可以通过实验测量得到。

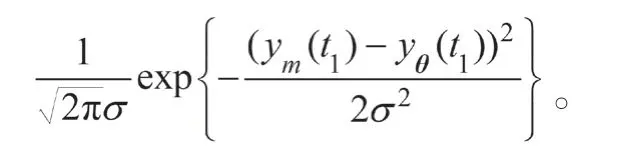
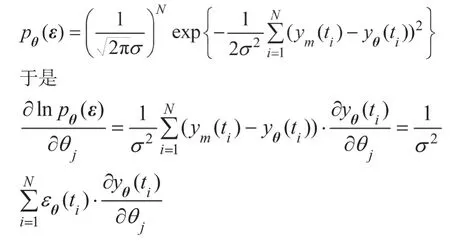
则根据Fisher信息的定义知

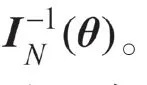
在此次教学案例设计中，我们选取了两个不同领域的例子，用来帮助学生理解不等式的深刻含义。通过以上两个案例的分析，让学生对枯燥的理论公式有了直观的理解和认识，让他们感受到Cramer-Rao不等式在科学研究和工程实践中的应用。上述两个案例虽然看上去计算量比较大，但是根据Cramer-Rao不等式的内容及Fisher信息的定义，均能很快得到无偏估计的Cramer-Rao下界。上述案例虽然来自不同的研究领域，但是其中涉及的参数估计的精度分析属于同一类型的统计问题。在案例运用时，一方面结合背景开阔学生视野，另一方面重点让学生领会统计原理、掌握统计方法，对于计算量可以根据情况进一步简化。案例2相比于案例1，拓展了试验设计的相关内容，能够让学生更加直观地感受Cramer-Rao不等式在实践中的重要作用，并在此过程中学会运用Cramer-Rao不等式。结合以上两个案例，可以在教学过程中通过讨论互动的方法，让学生总结利用Cramer-Rao不等式解决具体问题的方法和步骤，更加深入地理Cramer-Rao不等式的基本理论，从而更好地发挥案例教学法的作用。

三、结语

Cramer-Rao不等式在数理统计中具有重要地位。虽然Cramer-Rao不等式的教学内容便于理解，但是学生对于Cramer-Rao不等式在实际应用中能够解决什么问题、怎样解决问题缺乏直观认识。本文针对Cramer-Rao不等式案例资料有限的情况，查阅相关领域的前沿研究成果整理出两个案例，希望通过案例展示帮助学生将Cramer-Rao不等式的理论与实践紧密结合起来，锻炼学生发现问题、分析问题和解决问题的能力。