Temperature and strain sensitivities of surface and hybrid acoustic wave Brillouin scattering in optical microfibers

Yi Liu(刘毅) Yuanqi Gu(顾源琦) Yu Ning(宁钰) Pengfei Chen(陈鹏飞) Yao Yao(姚尧)Yajun You(游亚军) Wenjun He(贺文君) and Xiujian Chou(丑修建)

1Taiyuan University of Technology,Key Laboratory of Advanced Transducers and Intelligent Control System,Ministry of Education and Shanxi Province,Taiyuan 030024,China

2Taiyuan University of Technology,Institute of Optoelectronic Engineering,College of Physics and Optoelectronics,Taiyuan 030024,China

3Strong Digital Technology Co.,Ltd. (Thinvent),Nanchang 410000,China

4North University of China,Key Laboratory of Instrumentation Science and Dynamic Measurement Ministry of Education,Taiyuan 030051,China

5North University of China,College of Mechatronics Engineering,Taiyuan 030051,China

6North University of China,Science and Technology on Electronic Test and Measurement Laboratory,School of Instrument and Electronics,Taiyuan 030051,China

Keywords: Brillouin scattering,surface acoustic waves,hybrid acoustic waves,optical microfiber sensing

1. Introduction

Stimulated Brillouin scattering(SBS)in optical fiber is a third-order nonlinear effect[1]by photon-phonon coupling.[2]In standard optical fiber, the acoustic waves involved in SBS are bulk acoustic wave(BAW),in which the pump light both excites and interacts longitudinal and shear waves,producing backward-SBS(BSBS)and forward-SBS(FSBS),[3-6]respectively. The deviations between the pump light and the scattering light are Brillouin frequency shifts (BFS). The properties of fiber materials can be adjusted by the action of external physical field (stress, temperature, etc.), leading to corresponding changes in BFS of forward and backward scattering light. SBS has been studied intensely in applications such as forward/backward Brillouin sensors[7-11]and distributed/point fiber sensing.[12-17]Qianet al.realized the sensitive enhancement of a fiber laser sensor by Brillouin slow light.[18]Liuet al.realized a triple Brillouin frequency spacing Brillouin fiber laser sensor for temperature measurement.[19]Desmondet al.proposed a distributed forward Brillouin sensor based on light phase recovery.[20]

It has been proved that both photons and phonons in optical microfibers are strongly constrained and highly overlapped in space,[21,22]producing new type of BS driven by SAWs and HAWs.[23,24]Generated by the interaction between incident light and the outer surface of the optical microfibers, SAWs’travel velocity are approximately 0.87 to 0.95 times than that of the shear waves along the microfiber surface.[25]While HAWs are generated by the strong coupling of longitudinal and shear waves, and propagate at a medium speed between shear and longitudinal waves are in the microfiber. SAWs and HAWs exist in different positions of the optical microfiber,[26]and have different Brillouin spectrum characteristic.[27]The BFS and Brillouin gain are affected by the structure, material and size of the optical microfibers. The SAW and HAW BS sensing performance of microfiber is expected to break through the limitation of standard optical fiber sensing. Moreover, the SAW BS can be controlled or enhanced by smallcore and high air-filling fraction microstructured fibers[28]and the photo-elastic and moving-boundary effects,[29]and eliminated for one polarization mode at certain core ellipticities.[30]The SAW and HAW BS have been applied to characterize of subwavelength-diameter tapered silica optical fibers,[31]obtain the values of the elastic constants[32-34]and optical sensing and detection.[35-37]

In this paper, we demonstrate the temperature and strain sensitivities of SAW and HAW BS in optical microfibers,which is potential for new-type Brillouin fiber-optic sensing applications. We numerically simulate the frequencies of SAMs and HAMs using the elastodynamic equation including the electrostrictive stress[38-40]at 1µm diameter. Furthermore, the optical/acoustic distributions at 1µm diameter and the Brillouin spectrum of SAWs/HAWs with 1-1.3µm diameters are calculated, which are basically consistent with the reported results.[23]According to the influences of temperature and strain on material properties, the temperature/strain sensitivities and sensitivity-diameter slopes of the SAMs and HAMs are demonstrated from 1 µm to 1.3 µm diameters. In addition,it is shown that SAW and HAW BS can realize temperature and strain simultaneous sensing and have excellent sensing performance.

2. Theoretical analysis

2.1. Elastodynamic equation including electrostrictive stress

Electrostriction of an acoustic phonon is obtained from the interaction of two incident photons satisfying the previous phase-matching conditions. The exact contribution from each mechanism can be calculated by the elastodynamic equation including the electrostrictive stress to more accurately study and calculate the frequency and displacement distributions of the acoustic wave in optical microfibers. The elastodynamic equation can be written as

withci jklis the isotropic elastic matrix,χkli j=εimεjnpklmn,χkli jis the fourth-order polarization tensor,ε0andεijare the vacuum dielectric constant and the dielectric tensor of the medium, respectively.pklmnis the fourth-order photoelastic tensor,EkE∗lis the dyadic vector of the electric field. The phonon lifetime takes into account the elastic losses assuming a complex elastic tensor whose imaginary part is a constant viscosity tensor times frequency. This loss model is compatible with the usual assumption that theQ×f=5 THz is a constant for a given material, withQthe quality factor andfthe acoustic frequency.

The Brillouin gain factor and the backward Brillouin gain of acoustic mode can be written as[41]

2.2. Temperature and strain sensing principles

The temperature changes will affect the fiber’s four main material properties (refractive index, density, Poisson’s ratio and Young’s modulus) to influence the BFS (i.e., acoustic mode frequency). The effects of temperature and strain on material properties are[41]

withn0= 1.444,ρ0= 2203 kg/m3,γ0= 0.17,E0=72.553 GPa are the initial refractive index, density, Poisson’s ratio and Young’s modulus of fused silica at 27°C.ΔTis the temperature change value.

While the strain will induce elastic anisotropy in optical microfibers. The effective elastic tensor can be written as[42]

withλ=16 GPa andµ=31 GPa are the Lam´e constants of fused silica and°denotes the Hadamard product. ¯εzzis the tensile strain.

3. Results and discussion

3.1. SAW and HAW BS in optical microfibers

The cylindrical waveguide with 1µm diameter is numerically simulated based on a finite-element method.[43]The solid core made of silica is surrounded by air (n=1). With this size, the influence of radiation pressure is almost negligible in principle.[44]The optical power density of the fundamental guided optical mode in the silica bridge forλ=1550 nm is displayed in Fig. 1(a). The calculated effective refractive index is 1.1715. It can be indicated that a small part of the energy of the optical wave will leak out of the optical fiber from an evanescent field,but most of the energy of the optical wave is trapped in the optical fiber.

The Brillouin spectra of SAWs and HAWs are significantly changed because their propagation speeds are different from that of BAWs. The BFSs of SAWs and HAWs are～6 GHz and～9 GHz, respectively. In addition, the SAWs are extremely sensitive to the fiber surface change, and the HAWs will produce multi-peak Brillouin scattering structures due to the different coupling ratios of longitudinal and shear waves. We numerically simulate the frequencies of SAMs at 5.34 GHz(SAM1)and 5.67 GHz(SAM2),HAMs at 8.48 GHz(HAM1) and 9.16 GHz (HAM2) with 1 µm fiber diameter,which are basically consistent with the reported results.[23]Every normalized acoustic mode displacement and density distribution are shown in Figs.1(b)-1(i),respectively.It can be seen the acoustic mode energy density of the SAWs is limited to the air-silica interface of the optical microfiber,causing mechanical ripples of several picometers. Inside of the microfiber,the acoustic mode density gradually decreases with the distance from the surface. The acoustic mode energy density of the HAWs is still confined in the center of the optical microfiber.

Fig. 2. (a) Numerical simulation of the Brillouin spectra with optical microfiber diameter varying from 1µm to 1.3µm. (b)The acoustic frequency and Brillouin gain as a function of microfiber diameter.

Figure 2(a) shows the numerical simulation of the Brillouin spectra with an optical microfiber diameter varying from 1 µm to 1.3 µm. The frequency of SAM1 increases from 5.3452 GHz to 5.5321 GHz and the Brillouin gain decreases from 7.2324 W-1·m-1to 6.2128 W-1·m-1. In contrast, we noticed that SAM2 has a greater frequency variation than SAM1 in Fig. 2(b). The frequency of SAM2 increases from 5.6710 GHz to 6.0858 GHz while the Brillouin gain decreases from 2.9372 W-1·m-1to 4.3159 W-1·m-1.The Brillouin gains of SAMs gradually decrease with diameter increasing, caused by strong effect of the decreased microfibers diameter on the acousto-optic interaction. The frequency of HAM1 decreases from 8.4820 GHz to 7.8046 GHz and the Brillouin gain increases from 9.9569 W-1·m-1to 37.6959 W-1·m-1, while the frequency of HAM2 increases from 9.1623 GHz to 9.5497 GHz and the Brillouin gain decreases from 9.8159 W-1·m-1to 9.5659 W-1·m-1. The phase-matching condition leads to the differences of Brillouin spectra of acoustic frequencies under different diameters. The different trends of two HAMs with diameters result from the different coupling ratios of longitudinal and shear waves under the boundary conditions of the waveguide,causing changes in group sound velocity and BFS. Compared with the Brillouin gain of 0.4 W-1·m-1in single-mode fiber,microfiber sensing has higher signal-to-noise ratio.

3.2. Temperature and strain sensitivities

The temperature and strain sensitivities of optical microfibers can be calculated by the variation of BFS with temperature and strain. Due to the polymer cladding,the maximal tensile strain in standard optical fibers is limited to 2%,but naturally the elasticity of silica glass allows going up to 6%.[45]Using Eqs.(3)and(4),the BFS of 1µm diameter optical fiber can be calculated at different temperatures and strains (compared with 0°C and no strain),as shown in Figs.3(a)and 3(b),respectively.It can be found that the BFS of SAMs and HAM2 are almost linear with temperature and strain. The SAM1 and SAM2 have the comparative temperature and strain coefficients with 0.458 MHz/°C(0.432 MHz/°C)and 65.94 MHz/%(73.02 MHz/%). The temperature and strain coefficients of HAM2 are 0.928 MHz/°C and 264.53 MHz/%. The BFS of HAW1 is linear 0.660 MHz/°C with temperature, but nonlinear with strain because of strain-induced elastic anisotropy.The strain sensitivity decreases with the increase of strain,ranging from 82.54 MHz/%to 109.50 MHz/%.

Fig.3. (a)The temperature and(b)strain sensitivities of each acoustic wave mode are considered as a function of 1µm diameter optical fibers.

3.3. Temperature and strain sensitivities under different fiber diameters

The Brillouin resonances have high sensitivity to the geometric parameters of microfibers.[46]The temperature and strain sensitivities of each acoustic mode with a diameter varying from 1 µm to 1.3 µm as shown in Figs. 4(a) and 4(c),respectively. For unit consistency, write the strain sensitivity of 100 MHz/% as 0.01 MHz/µε. The insets show the acoustic mode density distribution at 1 µm, 1.16 µm, and 1.3 µm diameters, respectively. In order to study the relationship between temperature/strain sensitivities and diameter change,we plot the temperature/strain sensitivity-diameter slope of each acoustic mode with a fiber diameter varying from 1 µm to 1.3µm as shown in Figs.4(b)and 4(d),respectively. The temperature sensitivity-diameter slopeTd= dT/ddis the derivative of temperature sensitivity to fiber diameterd, and strain sensitivity-diameter slopeSd= dS/ddis the derivative of the strain sensitivity to the fiber diameterd.

It can be seen in Fig. 4(a) that the temperature sensitivities of the HAMs are significantly greater than that of the SAMs. As the fiber diameter changes from 1 µm to 1.3 µm, the temperature sensitivities of the SAMs gradually increase. The maximum temperature sensitivities of SAM1 and SAM2 are 0.557 MHz/°C and 0.568 MHz/°C at 1.3µm diameter,respectively,whereas those of the HAM1 and HAM2 are 0.744 MHz/°C at 1 µm diameter and 1.082 MHz/°C at 1.14µm diameter,respectively. It can be seen in Fig.4(b)that the temperature sensitivity-diameter slopes of the SAMs both are between 0.05 MHz/°C/µm and 0.25 MHz/°C/µm with diameter, while those of the HAMs are significantly changes.For instance,the temperature sensitivity-diameter slope of the HAM2 is-1.23 MHz/°C/µm at 1.3µm diameter. This means that the change in temperature sensitivity of-1.23 MHz/°C would be corresponding to the variation of one micrometer in fiber diameter.

It can be seen in Fig.4(c)that the strain sensitivity of the HAM2 is 0.0289 MHz/µεat 1.1µm diameter,which is significantly greater than those of the SAMs and HAM1.As the fiber diameter changes from 1 µm to 1.3 µm, the strain sensitivities of SAMs increase gradually,and the maximum values are 0.008 MHz/µεand 0.0078 MHz/µε, respectively. Whereas the strain sensitivity of HAM1 decreases with the increase of diameter. The green areas show the variation of strain sensitivity in the tensile strain of 1%-5%. Figure 4(d)shows the strain sensitivity-diameter slope of the SAMs are both between 1×10-4MHz/µε/µm and 5×10-4MHz/µε/µm, which is a small fluctuation compared to that of HAMs. For instance,the maximum strain sensitivity-diameter slope of the HAM2 is-0.0096 MHz/µε/µm at 1.3µm diameter. The green areas indicate that the strain sensitivity of HAM1 tends to increase uniformly with diameter under 1%-5%tensile strain.

Fig.4. (a)The temperature sensitivity and(b)sensitivity-diameters of each acoustic wave mode are considered as a function of the fiber diameter.(c)The strain sensitivity and(d)sensitivity-diameters of each acoustic wave mode are considered as a function of the fiber diameter. The insets in(a),(c)show the acoustic mode density distribution at 1µm,1.16µm,and 1.3µm diameters,respectively. The gray areas in(b),(d)highlight the temperature/strain sensitivity-diameter slope 0.05 MHz/°C/µm-0.25 MHz/°C/µm and 1×10-4 MHz/µε/µm-5×10-4 MHz/µε/µm,respectively.

3.4. SAW and HAW BS sensing performance

Four acoustic modes excited at 1 µm diameter optical fiber are linearly related to strain and temperature, and their temperature and strain sensitivities are different. Therefore,the relationship between BFS and temperature/strain sensitivity is established by selecting any two acoustic modes, as shown below to realize simultaneous sensing of temperature and strain:

withva0andvb0are any two of the acoustic mode frequencies at a temperature of 27°C and no strain, respectively.CTaandCTbare the temperature sensitivities ofva0andvb0.CεaandCεbare the strain sensitivities ofva0andvb0.

In addition to improving the sensing sensitivities of temperature and strain,reducing the temperature and strain errors will also improve the multi-parameter sensing performance.The measurement errors of temperature and strain are due to the inaccurate determination of acoustic mode frequencies,which ignores the errors within the transfer matrix. Assume that the maximum measurement errors of acoustic mode frequencyδva=va-va0andδvb=vb-vb0are equal, denoted byδv=0.1 MHz.[47]Theδvwill be transferred to the temperature errorδTand strain errorδε, with transfer temperature coefficientβTand strain coefficientβε, which may be expressed as[48]

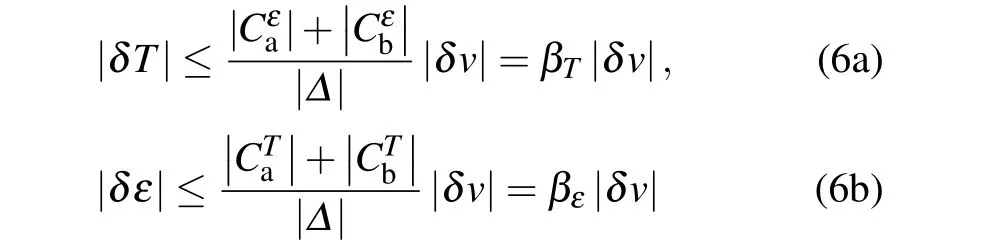
withΔ=CTaCεb-CTbCεanot equal to zero.

Through the above research, it is found that all the four acoustic modes in optical microfibers can realize multiparameter sensing. Temperature and strain errors were calculated by selecting two acoustic modes for comparison, as shown in Table 1. It can be seen the simultaneous sensing of SAW and HAW BS can achieve small temperature and strain errors. In particular, the temperature and strain errors of SAM1-HAM2 and HAM1-HAM2 combinations are as low as 0.47°C and 21.58µε,and 0.30°C-0.43°C and 15.09µε-19.80µε,respectively.

Table 1. Temperature and strain errors calculated by SAMs and HAMs.

Since the change of fiber diameter will affect the temperature and strain sensitivity of each acoustic mode,the temperature and strain errors of SAM1-HAM2 and HAM1-HAM2 combinations under different diameters are different,as shown in Fig. 5. The minimum errors of SAM1-HAM2 combination are 0.47°C and 20.96 µεat 1.06 µm, respectively. The minimum errors of HAM1-HAM2 combination are 0.30°C-0.34°C and 14.47µε-16.25µεat 1.08µm,respectively.Then their temperature and strain error coefficients increase with the diameter increasing,and the increase amplitude of SAM1-HAM2 combination was greater than that of HAM1-HAM2 combination.

Table 2 lists the temperature and strain errors based on SBS in different optical fibers. By comparison, the errors of multi-parameter sensing using acoustic modes in optical microfibers are smaller. In addition,when using microfiber sensing,the light field constraint ability is strong,the bending loss is low, and the bending radius can reach micron level, which can realize the manufacture of highly compact photon sensor.Microfiber has a large tensile strain of up to 6%,which is suitable for large strain sensing. And when Brillouin scattering is used in microfiber, it has large Brillouin gain, high signal-tonoise ratio and is easy to detect.

Table 2. The temperature and strain errors based on SBS in different optical fibers.

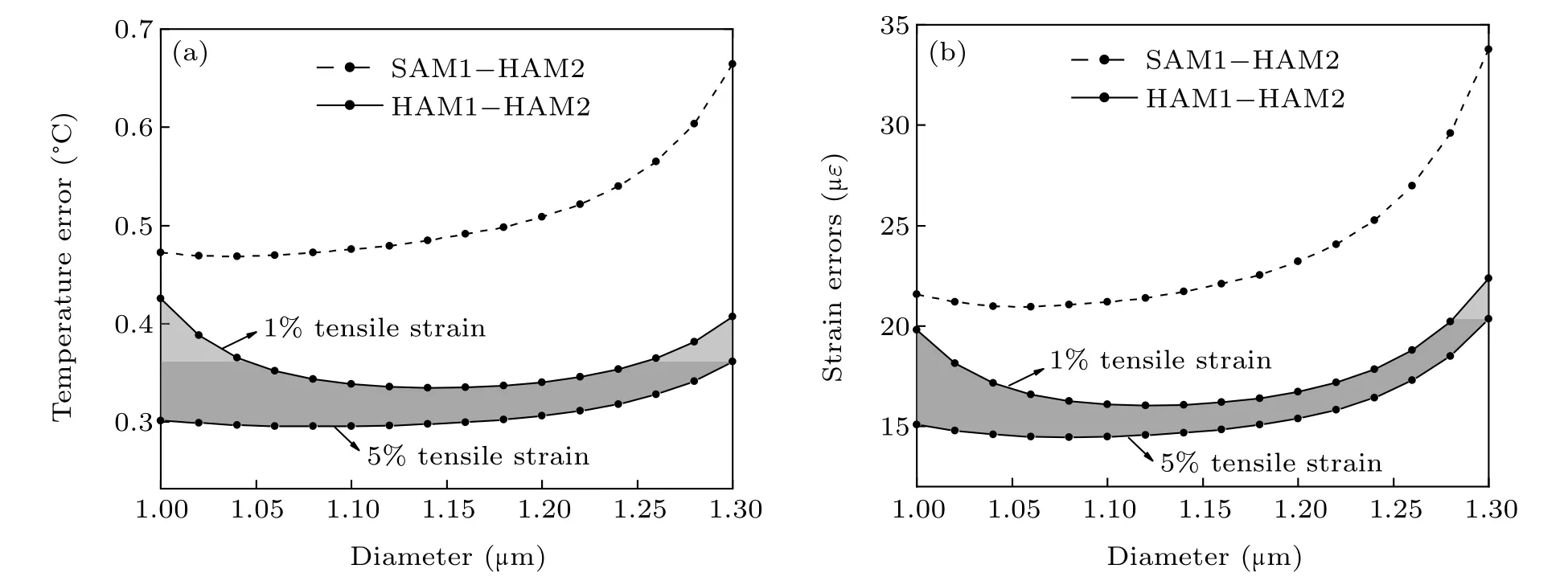
Fig.5. The temperature(a)and strain(b)errors of SAM2-HAM2 and HAM1-HAM2 acoustic mode combinations are considered as a function of the fiber diameter.

4. Conclusion

In conclusion, the temperature and strain sensitivities of SAW/HAW BS in optical microfibers with 1 µm-1.3 µm diameters are reported. It is found that the temperature and strain sensitivities of HAMs are as high as 1.082 MHz/°C and 0.0289 MHz/µεrespectively, which are significantly greater than those of the SAMs (0.568 MHz/°C and 0.0109 MHz/µε). Such results show that HAW BS is more suitable for high temperature and strain resolutions in microfiber sensing application.[53]Whereas, the temperature and strain sensitivity-diameter slopes of the SAMs range from 0.05 MHz/°C/µm to 0.25 MHz/°C/µm and 0.0001 MHz/µε/µm to 0.0005 MHz/µε/µm with diameter, which is much smaller than the value about-1.23 MHz/°C/µm and-0.0096 MHz/µε/µm of the HAMs at 1.3µm diameter. It suggests that the temperature and strain sensitivities of the SAMs are approximately the same with the slightly non-uniform diameter, indicating that SAW BS for temperature and strain sensing would put less stress on manufacturing constraints for optical microfibers. In addition,the applications of SAW and HAW BS in simultaneous sensing are analyzed.The combinations of SAM1-HAM2 and HAM1-HAM2 can obtain small temperature and strain errors. The minimum errors of HAM1-HAM2 combination are 0.30°C-0.34°C and 14.47 µε-16.25 µε, respectively. These results indicate that microfibers have great potential in point and distributed fiber sensing.

Acknowledgments

Project supported by the National Science Fund for Distinguished Young Scholars (Grant Nos. 61705157 and 61805167),the National Natural Science Foundation of China(Grant Nos. 61975142 and 11574228), China Postdoctoral Science Foundation (Grant No. 2020M682113), the Key Research and Development Projects of Shanxi Province, China(Grant No.201903D121124),and Research Project Supported by Shanxi Scholarship Council of China (Grant No. 2020-112).