Steering quantum nonlocalities of quantum dot system suffering from decoherence
Huan Yang(杨欢) Ling-Ling Xing(邢玲玲) Zhi-Yong Ding(丁智勇)
Gang Zhang(张刚)1,†, and Liu Ye(叶柳)3
1School of Electrical and Photoelectronic Engineering,West Anhui University,Lu’an 237012,China
2Key Laboratory of Functional Materials and Devices for Informatics of Anhui Higher Education Institutes,Fuyang Normal University,Fuyang 236037,China
3School of Physics and Optoelectronics Engineering,Anhui University,Hefei 230601,China
Keywords: quantum nonlocalities,quantum dot system,decoherence,steering
1. Introduction
Based on the background of the Einstein-Podolsky-Rosen (EPR) paradox,[1]quantum steering, as one of significant quantum nonlocalities different from classical world,was first illuminated for two-qubit system in Schr¨odinger’s efforts.[2,3]This quantum nonlocality describes a nonclassical phenomenon that the state of one side for a bipartite state can be steered via implementing measurement on the other side.[2-4]Subsequently, various quantum steering criteria embody seminal part in witnessing quantum steering and performing a variety of quantum information tasks.[5-15]These criteria mainly include steering criteria based on uncertainty relations,[16-21]fine-grained steering criteria,[22]linear and nonlinear steering criteria,[23-25]etc.The relevant investigations have been widely carried out in recent years.[26-29]Bell inequalities, including Clauser-Horne-Shimony-Holt(CHSH)inequality,[30]can quantify the strength of another kind of quantum nonlocality that the information can be encoded in the quantum correlations of the measurement outcomes between two parties shared by a two-qubit state.[31,32]The violations of Bell inequalities mean that the Bell nonlocality exists in the two-qubit state. A series of applications in quantum information processing depend on the Bell nonlocality,[33]such as multiparty conference key agreement,[34]communication complexity,[35]and self-testing.[36]


It is worth emphasizing that the coupling between the system and environment can accelerate the dissipation of quantum nonlocalities, which brings us great challenges to realize quantum information tasks. As a consequence, it is of essential importance in finding an avenue to battle against the degenerations of quantum nonlocalities. In addition, quantum dot systems have aroused wide attention due to their applications in quantum technologies.[55-64]For this reason, it is necessary to characterize and steer quantum nonlocalities of quantum dot system suffering decoherence. However, that is still lacking.In this work,the quantum steering,Bell nonlocality,and NAQC of quantum dot system coupled with nonunital and unital channels are investigated. The results reveal how the various parameters influence the quantum steering, Bell nonlocality, and NAQC of system. Also, in order to more effectively resist the dissipation of quantum nonlocalities of quantum dot system suffering decoherence so as to be more conducive to the realizations of various quantum information tasks via quantum dot system. We use local measurement reversal to explore the quantum nonlocalities and achieve the increases of quantum steering,Bell nonlocality,and NAQC of quantum dot system under the environmental influences.
The rest of the paper is organized as follows. Quantum dot system is briefly introduced in Section 2. The quantum steering, Bell nonlocality, and NAQC of quantum dot system are examined in Section 3. Considering nonunital and unital channels, the influences of environments on quantum nonlocalities of quantum dot system are investigated in Section 4.In Section 5,the enlargements of quantum steering,Bell nonlocality, and NAQC are realized for quantum dot system suffers decoherence. Finally,some conclusions are drawn in Section 6.
2. Quantum dot system
Considering the Hamiltonian of quantum dot in Ref.[65],which can be given by
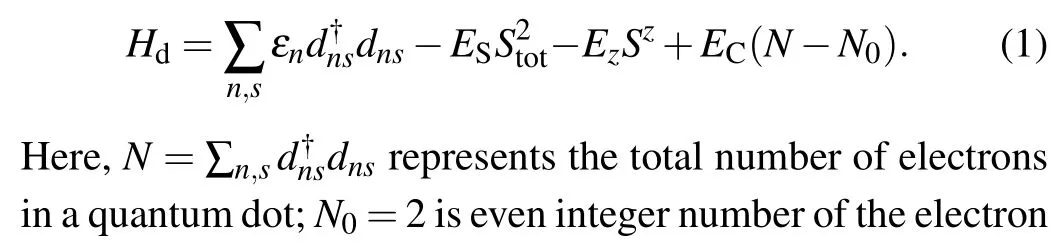



3. Characterizing quantum nonlocalities of quantum dot system
In this work, we use quantum steering criterion based on general entropic uncertainty relation to detect quantum steering. The CHSH inequality andl1norm of coherence are used to capture Bell nonlocality and NAQC, respectively.To begin with, we calculate the quantum steering of quantum dot system.ρAB= (I2⊗I2+a·σ ⊗I2+I2⊗b·σ+∑m,n cmnσm ⊗σn)/4(m,n ∈{x,y,z})is the state shared by Alice and Bob, a set of measurementsAk ⊗Bkis implemented on Alice and Bob,respectively. The quantum steering can be witnessed through the violation of steering criterion based on the general entropic uncertainty relation,[18]viz.


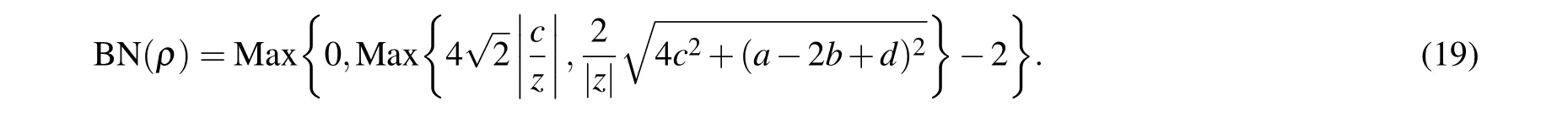

In order to investigate the influences of temperatureTon quantum steering, Bell nonlocality, and NAQC, we characterize the dependence of quantum steering, Bell nonlocality, and NAQC on temperatureTin Fig. 1. As demonstrated from Fig. 1(a), the quantum steering, Bell nonlocality, and NAQC sharply degenerate withthe increase of temperature after a short freezing process. In contrast, the NAQC of system is most vulnerable,and it is easily affected by enhancing temperature. The sudden death of NAQC takes place at lower temperature. The reasons for the results can be explained as follows. The state of quantum dot system can be described byρ=∑4i=1pi|φi〉〈φi|.[70]Here,pi= e-Ei/KT/tr(e-H/T) is the probability distribution. For the settings of parameters in Fig. 1(a), the state of quantum dot system lies in|φ4〉(i.e.maximally entangled states) atT=0. For this reason, different nonlocalities reach the corresponding maximum values atT=0 in Fig.1. After a short process of increasing temperature,state|φ4〉of quantum dot system gradually mixes with the higher energy levels|φ1〉,|φ2〉,and|φ3〉. The degree of mixing is enhanced with temperature rising. The results are responsible for the situations that quantum steering.The Bell nonlocality and NAQC sharply dissipate with the increase of temperature after a short freezing process. If parameterk0is increased to 7, as displayed in Fig. 1(b), quantum steering, Bell nonlocality, and NAQC can effectively battle against the effect of temperature. To be clarity,the three quantum nonlocalities experience a relatively long freezing process,and these traits are different form the ones in the scenario ofk0=3.The reason of freezing these quantum nonlocalities is that the increase ofk0effectively restrains the mixing of the state|φ4〉and the higher energy levels(|φ1〉,|φ2〉,and|φ3〉)at low temperature. In addition,the degenerative tendencies of these quantum nonlocalities in the case ofk0=7 are slower than the ones in the case ofk0=3. That is to say,the enlargement ofk0can effectively resist the effects of temperature on the quantum steering,Bell nonlocality,and NAQC.

Fig.1. Curves of quantum steering,Bell nonlocality,and NAQC with respect to temperature T for(a)k0=3 and r=0.5,and(b)k0=7 and r=0.5.
Now, we come to focus our attention on quantum steering, Bell nonlocality, and NAQC of quantum dot system under different parameterr, as depicted in Fig.2. As described in Fig. 2(a), the increase ofrcannot affect quantum steering nor Bell nonlocality nor NAQC in the initial stage. These quantum nonlocalities are frozen at different fixed values, respectively. However, quantum steering, Bell nonlocality, and NAQC sharply decrease if theirrvalues reach corresponding critical values, and disappear eventually. The results can be understood as follows. The quantum dot system is in almost maximally entangled state|φ4〉in the case of(k0=7,T=0.1,r=0),and the increase ofrcannot break the situation.Consequently,the quantum steering,Bell nonlocality,and NAQC are frozen in the initial stage. The mixing ratios of|φ1〉,|φ2〉,and|φ3〉(especially separable states|φ2〉) in quantum dot system are conspicuously enhanced when theirrvalues reach corresponding critical values. Hence these quantum nonlocalities sharply dissipate and disappear eventually. The NAQC,as the most fragile quantum nonlocality, dies at weakerr. The influences ofron quantum nonlocalities under the condition ofT=0.5 (Fig. 2(b)) are different from those under the condition ofT=0.1 (Fig. 2(a)) The increase of temperature from 0.1 to 0.5 leads to the fact that the state|φ4〉of quantum dot system mixes with|φ1〉,|φ2〉, and|φ3〉atr=0. The mixing ratios of|φ1〉,|φ2〉, and|φ3〉(especially|φ2〉) increase with the growingr. The mechanisms are responsible for the facts that the freezing phenomena of quantum nonlocalities are destroyed by increasing the temperature. The quantum steering,Bell nonlocality,and NAQC gradually decay with the enlargement ofrin Fig.2(b).
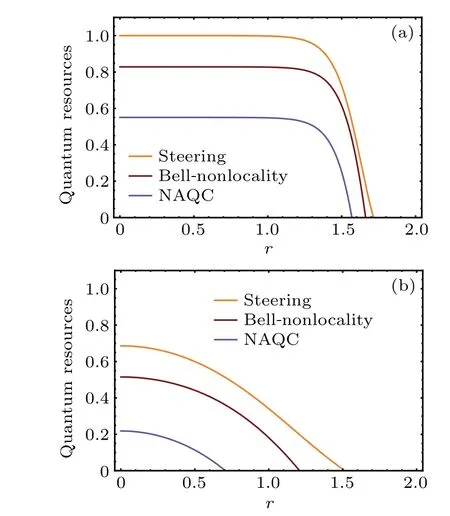
Fig.2. Curves of quantum steering,Bell nonlocality,and NAQC with respect to parameter r for(a)k0=7 and T =0.1,and(b)k0=7 and T =0.5.
At the last stage, the dependence of quantum steering,Bell nonlocality, and NAQC on parameterk0are characterized in Fig. 3. It is demonstrated that the quantum dot system cannot achieve quantum steering nor Bell nonlocality nor NAQC at weakk0. The system can only achieve these quantum nonlocalities ifk0reaches the critical values,respectively.After that,the quantum steering,Bell nonlocality,and NAQC are enhanced withk0growing. Finally,the quantum steering,Bell nonlocality, and NAQC are frozen due to the strong parameterk0. The mechanisms of the above phenomena can be formulated as follows. If thek0is weak, the state of quantum dot system is dominated by the separable state|φ2〉,therefore,the three quantum nonlocalities cannot be detected in this situation. Of particular note is that the mixing ratios of|φ2〉and|φ4〉in the state of quantum dot system will be swapped by increasingk0. The state of quantum dot system is gradually dominated by the maximally entangled state|φ4〉withk0increasing. Thus, quantum steering, Bell nonlocality, and NAQC can be captured at critical values ofk0. Subsequently,these quantum nonlocalities strengthen ask0goes up. Finally,these quantum nonlocalities are frozen at strongk0. Also,one can find from Figs.3(a)and 3(b)that the increase ofrcannot affect the tendencies nor characteristics of different quantum nonlocalities, but can affect only the critical valuek0of the quantum nonlocality.

Fig.3. Curves of quantum steering,Bell nonlocality,and NAQC with respect to parameter k0 for(a)T =0.1 and r=0.5,and(b)T =0.1 and r=1.
4. Investigating quantum nonlocalities of quantum dot system under decoherence
In this section, we observe the quantum steering, Bell nonlocality, and NAQC of system influenced by different decoherence channels. Considering that particle A and particle B of the quantum dot system are subjected to the effect of amplitude damping(AD)channel(a nonunital noise). The Kraus operators of AD channel can be written as[74]

wherep=1-e-Γt. The output state can be obtained as follows:

The detectable quantum steering ofρADcan be calculated and indicated below:

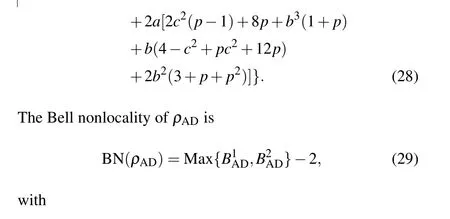

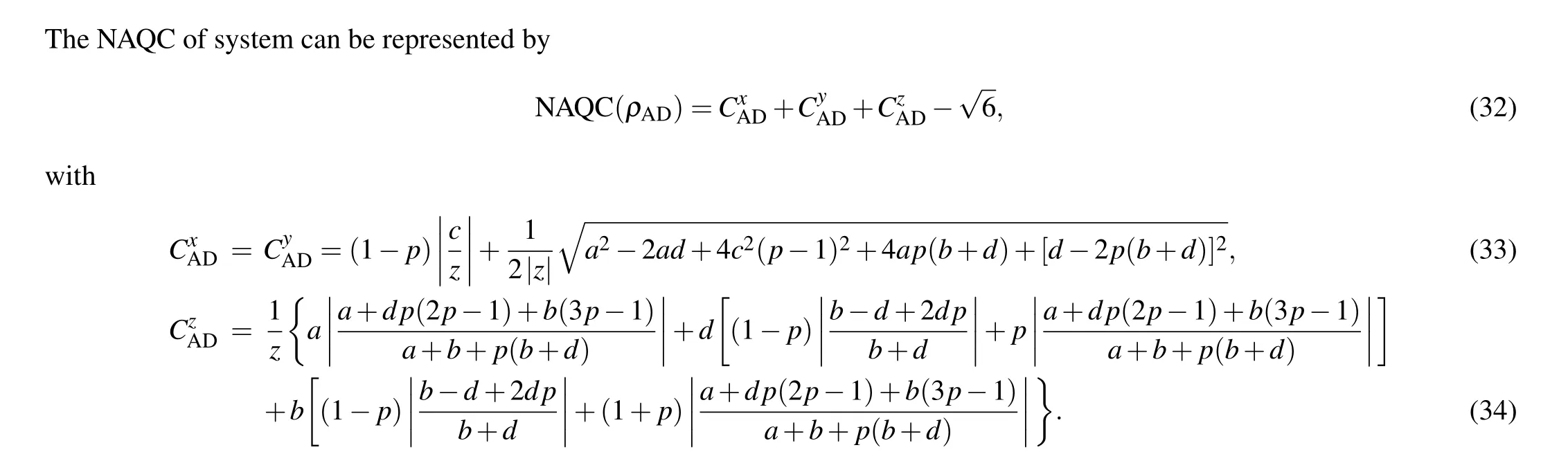
To examine the influences of AD channel on quantum steering, Bell nonlocality, and NAQC of quantum dot system,we herein provide quantum steering,Bell nonlocality,and NAQC each as a function of channel parametertas indicated in Fig. 4. Our results reveal that the quantum steering, Bell nonlocality, and NAQC decrease astgoes up. The effect of AD channel gives rise to the fact that the freezing phenomena of quantum steering,Bell nonlocality,and NAQC cannot take place in quantum dot system. Besides this, the increase ofΓfrom 0.5 to 2 as indicated in Figs.4(a)and 4(b)enhances the influences of AD channel on quantum nonlocalities, and induces the results that the sudden death of quantum steering,Bell nonlocality, and NAQC occur more rapidly. By investigating,we reveal that the eigenvector ofρADis consistent with that ofρ. That is to say,theρADcan also be characterized by the probabilistic combination of|φi〉(i=1,2,3,4). The above phenomenon can be attributed to the mechanism that the coupling between noise channel and quantum dot system reduces(increases)the mixing ratio of|φ4〉(|φ2〉)in the state of quantum dot system, and enhances the dissipation of information stored in quantum dot system. The stronger the channel parameterstandΓ,the more obvious the coupling is.
Now, we turn our attention to investigating the quantum steering, Bell nonlocality, and NAQC of quantum dot system suffering unital channel, namely, phase damping (PD) channel. The Kraus operators of PD channel are[74]

TheρPDcan also be represented by the probabilistic combination of|φi〉(i=1,2,3,4). One can obtain the detectable quantum steering ofρPD,
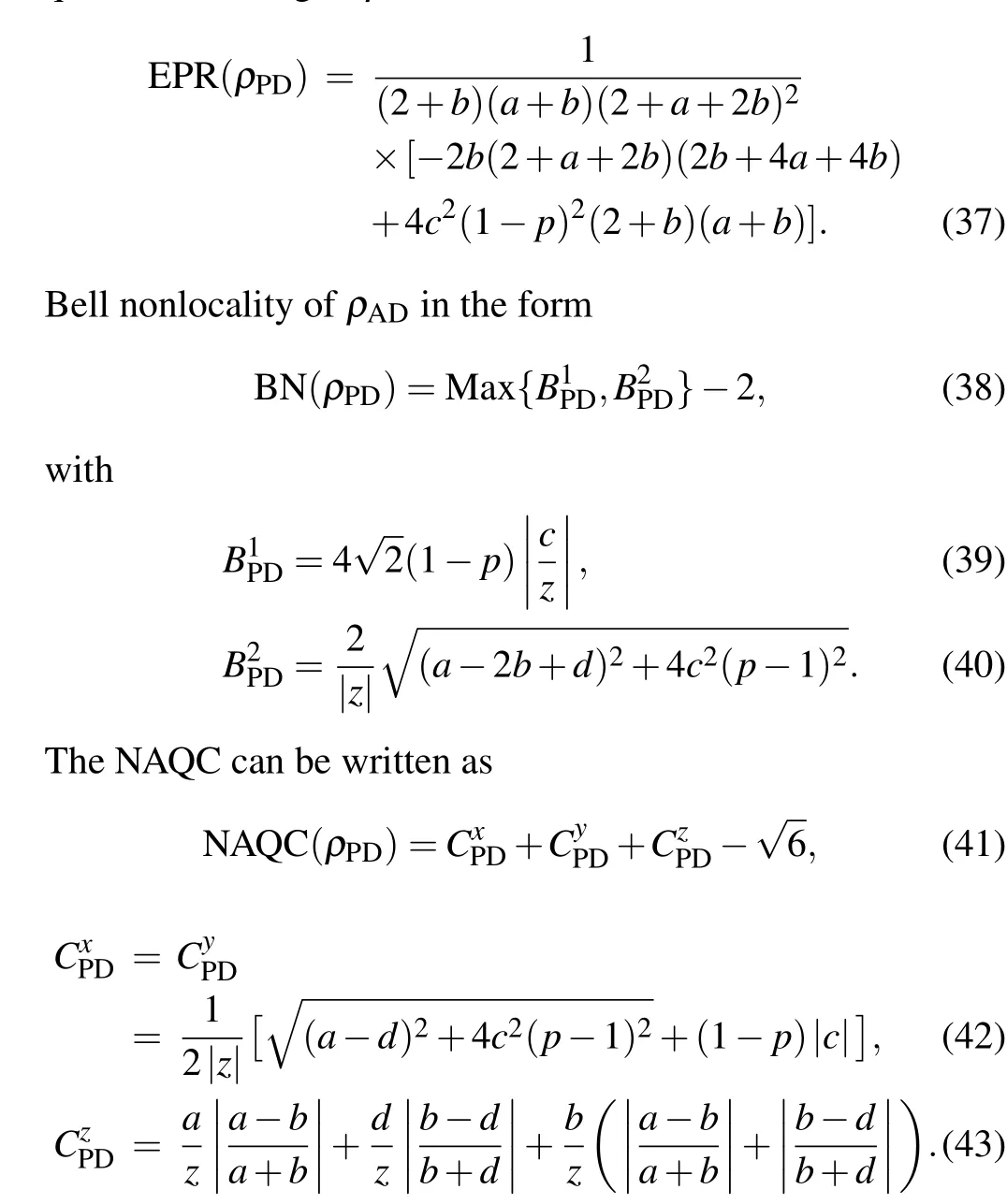
Figure 5 shows the curves of quantum steering,Bell nonlocality, and NAQC with respect to parametertof PD channel. The dynamics and mechanisms of these quantum nonlocalities under the influence of PD channel are similar to those under the influence of AD channel in Fig. 4. Quantum steering, Bell nonlocality, and NAQC degrade with increasingincreasing. The enlargement ofΓsuppresses the amplitude of quantum steering,Bell nonlocality,and NAQC.
Fig. 4. Curves of quantum steering, Bell nonlocality, and NAQC with respect to channel parameter t at k0=5,r=0.5,T =0.2: (a)Γ =0.5 and(b)Γ =2.

Fig.5. Couves of quantum steering,Bell nonlocality,and NAQC with respect to channel parameter t at k0=5,r=0.5,T =0.2,and Γ =0.5(a)and Γ =1(b).
5. Controlling quantum nonlocalities for quantum dot system suffering decoherence
The results obtained above reveal that the AD and PD noise channels strongly influence quantum steering,Bell nonlocality, and NAQC of the quantum dot system. In this scenario,we investigate the lifting quantum steering,Bell nonlocality, and NAQC for the quantum dot system coupling with AD channel and PD channel by implementing measurement reversal. The measurement reversal is one of uncollapsed partial measurements,and the operator can be expressed as[75]

One can derive the detectable quantum steering ofρAD-r,viz.

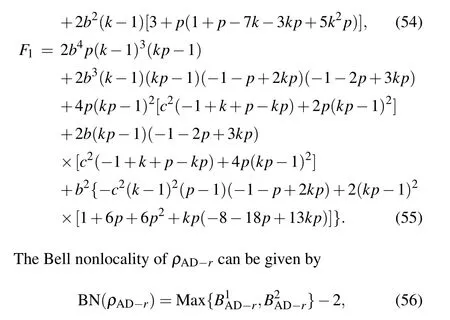
with

Next,we come to probe the quantum dot system suffering the PD channel. If one perform the measurement reversal on particle A and particle B ofρPD,the final state is represented byρPD-r,and the corresponding nonzero matrix elements are
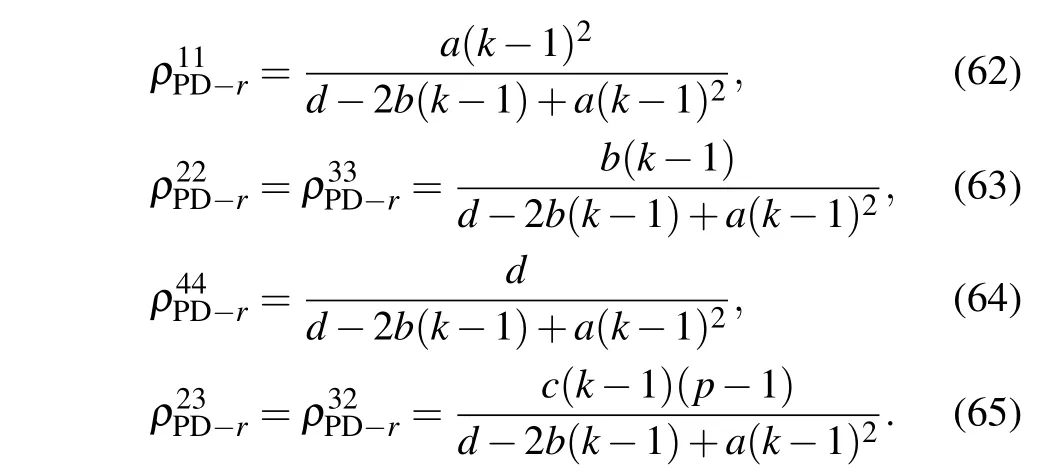
One can attain the detectable quantum steering ofρPD-r,namely,
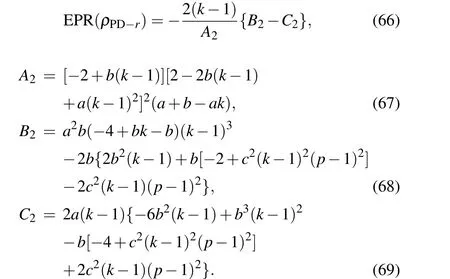

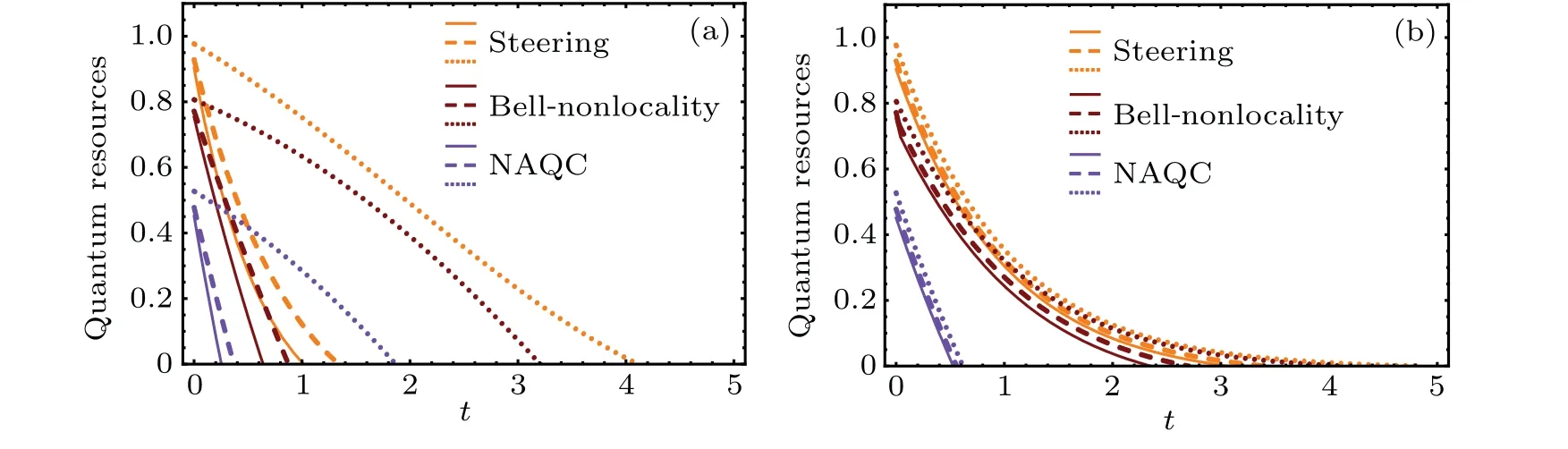
Fig.6. Curves of quantum steering,Bell nonlocality,and NAQC with respect to channel parameter t at k0=5,r=0.5,T =0.2,and Γ =0.5,indicating the results of(a)AD channel and(b)PD channel, with solid curves denoting the results of k=0, dashed curves for the results of k=0.3,and dotted curves for the results of k=0.9.
In order to demonstrate the effects of measurement reversal on quantum nonlocalities of quantum dot system in AD channel and PD channel, we characterize quantum steering,Bell nonlocality,and NAQC of system as a function of channel parametertunder different operation strengths(k=0,0.3,0.9)of measurement reversal in Fig.6. It is important to mention here that the measurement reversal does affect neither of the eigenvectors of the system,viz. theρAD-randρPD-rare still the probabilistic combination of|φi〉(i= 1,2,3,4), respectively. Owing to the fact that the measurement reversal can significantly increase the mixing ratio of|φ4〉in the state of quantum dot system suffering the AD channel,and effectively suppress the dissipation of information stored in quantum dot system.Accordingly,the measurement reversal can effectively enhance the quantum steering,Bell nonlocality,and NAQC of quantum dot system influenced by the AD channel,which are revealed in Fig.6(a). The stronger the operation strength,the more obvious the enhancement of quantum nonlocality is. If operation strengthkincreases to 0.9,the amplitude of quantum steering,Bell nonlocality,and NAQC are remarkably strengthened. The degenerating trends of these quantum nonlocalities become relatively gentle. These traits are responsible for the delay of sudden death of quantum nonlocality, and the quantum nonlocalities of quantum dot system can effectively restrain the influence of AD noise with the help of the measurement reversal.Additionally,the measurement reversal can also realize the increases of quantum steering,Bell nonlocality,and NAQC of quantum dot system suffering PD channel,as exhibited in Fig. 6(b). Note that compared with the results of AD channel in Fig.6(a),the influences of measurement reversal on different quantum nonlocalities of quantum dot system under PD channel are not significant. Even if the operation strengthkincreases to 0.9, the enlargement of quantum steering, Bell nonlocality,and NAQC are not obvious.The results can be explicated as follows. Even if the operation strengthkis strong,the measurement reversal cannot effectively influence the mixing ratio of|φ1〉,|φ2〉,|φ3〉,and|φ4〉in the state of quantum dot system suffering PD channel, and cannot obviously suppress the dissipation of information stored in quantum dot system either. For this reason, measurement reversal is more effective for steering quantum nonlocalities of quantum dot system suffering the AD channel.
6. Conclusions
The quantum steering, Bell nonlocality, and NAQC of quantum dot system coupling with decoherence are investigated in this work. The results reveal that the quantum steering, Bell nonlocality, and NAQC of quantum dot system can be frozen by reducing temperature. The degeneration of parameterk0can destroy these freezing phenomena at different temperatures. The increases ofk0can help the quantum steering,Bell nonlocality,and NAQC to resist the influence of temperature. The enlargement of parameterrcannot affect quantum steering nor Bell nonlocality nor NAQC at low temperature. These quantum nonlocalities sharply decline at critical values ofr. The freezing phenomena of quantum nonlocalities at different values ofrdisappear via enhancing the temperature. The quantum steering, Bell nonlocality, and NAQC gradually strengthen withk0increasing. And these quantum nonlocalities are frozen ultimately. One cannot capture the quantum steering nor Bell nonlocality nor NAQC of quantum dot system at high temperature, strongr, and weakk0. The NAQC, as the most fragile quantum nonlocality, is most easily affected by different parameters of system. Also, it turns out that quantum steering, Bell nonlocality, and NAQC decrease as the parametertof AD channel and PD channel go up. The enlargement of channel parameterΓresults in the fact that the sudden death of quantum steering, Bell nonlocality, and NAQC take place more rapidly. It is worth emphasizing that the measurement reversal can effectively control and strengthen the quantum steering,Bell nonlocality,and NAQC of quantum dot system suffering noise channel. The stronger the operation strength,the more effective the protection of quantum nonlocality is.The influences of measurement reversal on these quantum nonlocalities of quantum dot system coupling with AD channel are stronger than those of quantum dot system coupling with PD channel.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No. 12175001), the Natural Science Research Key Project of the Education Department of Anhui Province, China (Grant Nos. KJ2021A0943 and KJ2020A0527), the University Synergy Innovation Program of Anhui Province, China (Grant No. GXXT-2021-026), the Anhui Provincial Natural Science Foundation, China (Grant Nos. 2108085MA18 and 2008085MA20), the Key Project of Program for Excellent Young Talents of Anhui University,China(Grant No.gxyqZD2019042),the Open Project of Key Laboratory of Functional Materials and Devices for Informatics of Anhui Higher Education Institutes,China(Grant No.FMDI202106),and the Research Start-up Funding Project of High Level Talent of West Anhui University,China(Grant No.WGKQ2021048).
- Chinese Physics B的其它文章
- Erratum to“Accurate determination of film thickness by low-angle x-ray reflection”
- Anionic redox reaction mechanism in Na-ion batteries
- X-ray phase-sensitive microscope imaging with a grating interferometer: Theory and simulation
- Regulation of the intermittent release of giant unilamellar vesicles under osmotic pressure
- Bioinspired tactile perception platform with information encryption function
- Quantum oscillations in a hexagonal boron nitride-supported single crystalline InSb nanosheet

