基于空间深度置信网络的风速预测优化方法*

许皓宇 ，薛 巍 ，张 涛 ，谢洪亮

(1.清华大学 计算机科学与技术系，北京 100084；2.远景能源(南京)软件技术有限公司，上海 200050)

0 引言

随着环境污染以及能源紧缺问题的加剧，风能作为一种可再生的清洁能源在世界各国得到了迅速的发展。目前，风力发电在我国的电源结构占比已超过了核能，仅次于火力和水力发电。而在欧美各国，风力发电的总电量占比已经超过10%。风速变化非常剧烈，具有很强的波动性和随机性，导致风力发电无法保证稳定的输电功率，为保证供电网络的稳定，大量的风电能源被浪费。同时，由于风力资源的不稳定，一旦风电功率达到穿透功率，将严重威胁电网的安全运行。风速和风功率的准确预测对于风能的进一步的开发和利用至关重要。

目前，针对风速的长短期预测已经进行了大量的研究。传统的数值天气预报以大气动力学方程为基础，从当前天气状态逐步向前迭代积分来预报未来的风速。数值天气预报模式包含了大规模偏微分方程求解，需要消耗大量的计算资源。随着人工智能和机器学习技术的快速发展，将基于数据的机器学习技术应用于风速预测得到了逐步深入的研究。

机器学习算法利用历史数据来训练模型，在模型训练好后就可以基于过去的特征预测未来风速，相比数值天气预报，模型推理需要的计算资源大大减少。一些经典的机器学习模型包括线性回归(Linear Regression)、可支持向量机回归(Support Vector Machine)和不同结构的人工神经网络(Artificial Neural Network)等都被用于短期(0～12 h)的风速预报[1-6]。这些工作首先将历史数据转化为特征和预测目标，进行简单的数据预处理后使用模型训练和学习，在短期的风速预测上能够取得不亚于数值天气预报的精度[7]。

上述机器学习预测方法在选取特征时均局限于单一地点风速和相关气象因子(这种预测技术称之为单点预测)，没有考虑到风速的空间特性。风速的物理特性决定了风速在区域内的分布存在一定的规律并满足一定的约束[8]。受到不同地形及风速的不稳定性的影响，这些规律或约束很难用确切的数学函数表示。因此，本文提出使用深度置信网络(Deep Belief Network，DBN)从数据中学习和挖掘复杂混沌的风速的空间规律和约束，并利用学习到的规律和约束重构和改善单一地点的风速预测结果。

深度置信网络是一个概率生成模型，能够建立输入变量之间的联合分布，通过学习到的联合分布DBN 可以完成特征提取、数据压缩与重构、图像降噪等任务。经过DBN 提取的特征(即隐藏层节点)可以将音乐分类的准确率提高14%[9]。将DBN 应用于“瑞士卷”数据压缩，可以无损地将三维数据压缩至两维再恢复[10]。经过训练的DBN 网络也可以重构有噪声的原始数据达到降噪的目标。DBN 也被用于提取不同气象因子(风速、温度、气压、湿度)之间的规律用于重构天气状态[11]。

本文比较了多种机器学习算法的12～72 h 单点风速预测性能，随后使用DBN 改善了其中误差最低的单点预测结果，经过DBN 重构的预测误差下降达到平均0.4 m/s。

1 风速预测问题

按照预测目标、时间范围，风速预测可以分为短期、中期和长期预测，不同时间尺度的预测及其主要应用见表1。

表1 不同时间尺度风速预测和应用场景

表1 中对于不同时间尺度的风速预测的划分并不是严格的。我国能源局发布的《风电功率预测功能规范》中规定了超短期和短期预测两种预测任务[12]。其中超短期预测要求预测未来0～4 h 的风速和风功率，短期预测要求预测0～72 h 的风速和风功率，时间分辨率均为15 min。

目前用于风速预测的主要方法包括数值天气预报和统计回归(机器学习)模型。统计回归模型也是后续本文单点试验所选用的模型。

尽管在短期风速预测上机器学习方法取得了成功，但在中长期(12～72 h)预测上机器学习却无法达到数值天气预报的精度。这是因为中长期预测中预测目标和特征的相关性相比短期预测大大降低，且在几十个小时的时间里，很多天气现象都会对风速产生明显的影响，再加上风速具有很强的波动性，导致中长期风速预测难度显著增加。而中长期的风速预测对于风电场的任务调度、成本和收益估算等具有重要的意义，因此本文致力于提高中长期风速预测的精度。

2 深度置信网络

2.1 DBN 模型结构和训练

深度置信网络(DBN)是一个包括多层隐藏层的神经网络模型[13]。DBN 既可以解决有监督学习中的分类问题，也可以训练一个无监督学习的生成模型。本文主要采用用于重构的无监督生成型DBN，其结构如图1 所示。

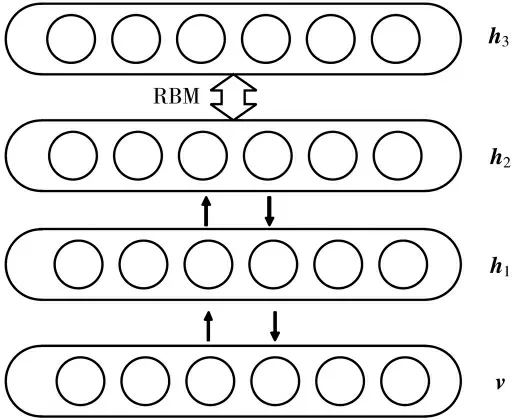
图1 DBN 网络基础结构[13]

图1 中每一层都是一个受限玻尔兹曼机(Restricted Boltzmann Machines，RBM)，每一层的输出作为下一层的输入。每一层的RBM 包含可见层v 和隐藏层h，b 为可见层偏移量，c 为隐藏层偏移量，W 为可见层和隐藏层之间的权值矩阵。模型的能量函数形式如式(1)：

自可见层开始向上依次训练每一层RBM 完成无监督DBN 的训练[14]。

2.2 针对风速预测空间深度置信网络

风速的空间特性来源复杂，同时受到地形的影响，很难用统一固定的数学函数表示。文献[8]研究了在同一方向上相距10～30 km 的多个地点的风速情况，发现风速呈现很强的时延相似性。此外，在一些特殊地形，例如盆地、山谷，风速也将受到一定的约束。由于地形的影响，一个地区的规律和物理约束很难推广到其他区域。因而，本文采用深度置信网络来通过历史数据自动学习和挖掘具体某一地区内空间风速分布的规律。

DBN 可以从数据训练和学习到变量的联合概率分布。如果将某一地区内多个观测点的历史风速数据输入到DBN 中，DBN 就可以学习到风速的空间分布规律(即联合分布)，而这些内在的规律和特征在DBN 内部通过权值矩阵、偏移量和隐藏层节点来存储和表示。在完成DBN 的训练后，DBN 可以对输入的一组空间风速预测进行重构。重构过程中，DBN 将判断输入的预测风速是否满足之前学习到的风速分布规律并根据规律对预测风速进行修正，生成新的一组风速预测。新的风速预测是DBN 在原预测基础上根据历史空间风速分布规律修改得出的。

基于DBN 的风速预测改进算法的具体流程如下：

(1)构建训练数据集x1，x2，x3，…，xn，其中xi代表时刻i 风场风速向量，包含了d 个地点的风速值。

(2)确定DBN 的结构和参数(层数、每层节点数、训练代数、学习率)，使用训练数据集无监督训练DBN。

3 面向风速预测的DBN 参数选择与训练

同其他深度学习模型一样，DBN 的参数对于DBN的性能影响非常大。DBN 的参数包括通过训练更新的模型参数(权值矩阵和偏移量〈b，c，W〉），以及需要在训练前决定的学习率η、训练迭代次数和网络结构参数等，这些参数称为超参数(hyper parameter)。通过训练更新的权值矩阵和偏移量取决于训练数据和超参数，选择合理的超参数对于DBN 性能具有重要的意义。

在监督学习中会定义预测和标签的损失函数，最终选择损失函数最低的超参，而无监督DBN 的目标是减少重构后的风速预测误差，定义重构后的预测风速与观测风速之间的均方根误差(Root Mean Squared Error，RMSE)为评价指标，即选取一组超参使得DBN 重构后的风速预测结果RMSE 最低。

传统的自动超参调优和选择算法包括网格搜索(Grid Search)、随机搜索(Random Search)。网格搜索在超参数空间建立网格，需要进行的采样(模型训练)次数随超参个数指数级增长。网格搜索会在不重要的超参上浪费大量的采样，导致耗费大量的计算资源，因此网格搜索并不适合训练成本昂贵的DBN 超参调优。文献[15]则通过实验和理论分析证明随机搜素相比网格搜索更加高效，能够以更少的采样次数和计算成本寻找到更优超参(更优模型)。为了能够以尽可能低的成本完成超参调优和选择，本文采用代理模式优化(Surrogate-Based Optimization)。代理模式优化通过对目标优化问题建立一个代理模式来预测每一组超参数的模型训练结果。代理模式基于统计回归方法构建，与真实模式有很强的相似性，计算成本低廉，可以进行大量采样。通过在代理模式进行充分的采样和搜索，多数无意义的搜索和采样将被过滤，每一组优质的候选超参数根据代理模式生成，进行真实模型训练后更新和改进代理模式。随着代理模式的精确度不断提高，最终能够寻找到最优超参数，即最优DBN 模型。通过代理模式优化来进行DBN 超参调优和选择的流程如图2 所示。文献[16]、[17]使用代理模式优化对大量的深度学习和传统的机器学习模型进行超参调优，结果表明，代理模式优化的性能明显优于随机搜索、网格搜索等传统算法。

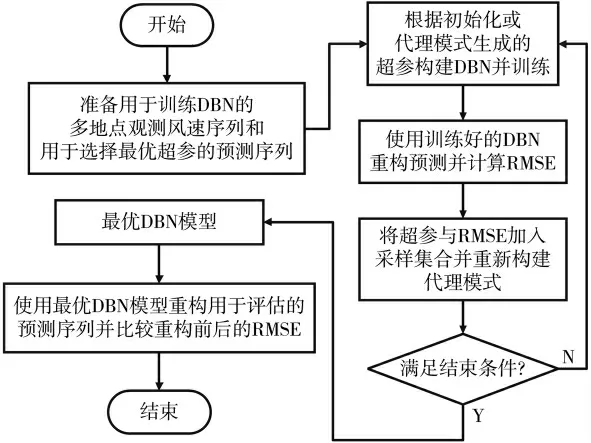
图2 DBN 模型超参选择、训练和重构流程

4 单点风速预测

单点风速预测指的是利用单一站点的历史风速来预测该站点未来风速的技术。本文选择了4 种具有代表性的机器学习模型进行单点预测，包括：线性回归(Linear Regression)[18]、梯度提升回归树(Gradient Boosting Regression Tree，GBRT)、支持向量机回归(Support Vector Regression，SVR)和高斯过程回归(Gaussian Process，GP)。

线性回归是应用最广泛也是最简单的回归模型，其训练成本非常低，适合处理高维稀疏特征空间的分类和回归问题[18]。相比线性回归，其他3 种模型都是非线性模型。梯度提升回归树是决策树类模型的一种，相比于单决策树模型，它通过大量简单的决策树组合克服了单决策树模型容易过拟合的缺陷，同时通过boosting 思想保证了收敛速率，具有训练速度快、对异常数据鲁棒性强等优点[19]。支持向量机回归利用核函数将特征空间映射到新的特征空间从而实现非线性回归。高斯过程回归则通过建立训练数据的联合分布来解决回归问题，能够根据特征预测概率分布。

本文选取了国内某区域内9 个测风塔一年的历史数据来进行单点风速预测实验，每个测风塔每隔10 min记录一次观测数据，包括风速、温度和气压。预测时选取过去7 天的历史数据作为输入特征，分别以未来12 h和未来72 h 的观测作为预测目标，每个模型都进行了五折交叉验证。表2 和表3 展示了使用4 种模型对每个测风塔进行12 h 和72 h 预报的RMSE。

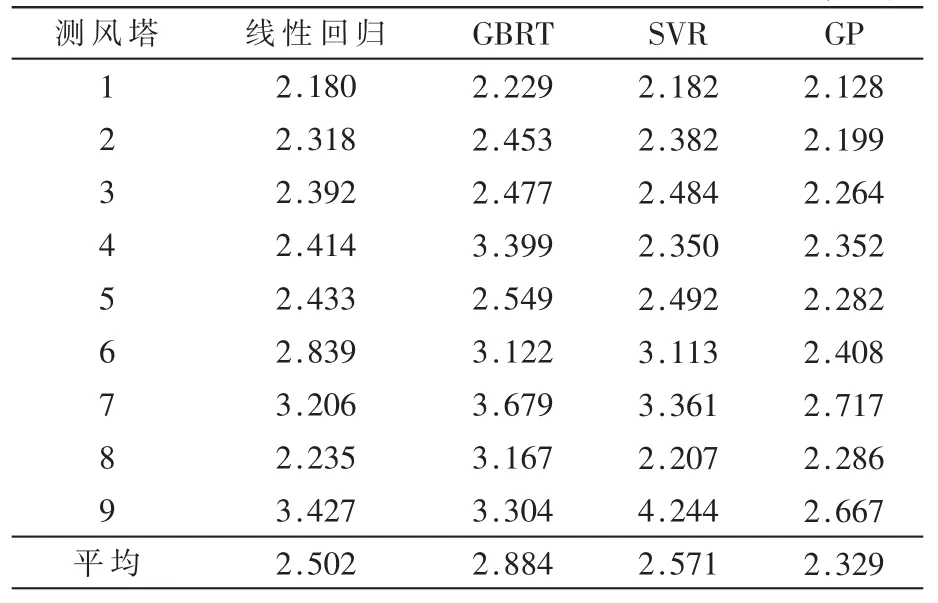
表2 12 h 风速预测实验 (m/s)

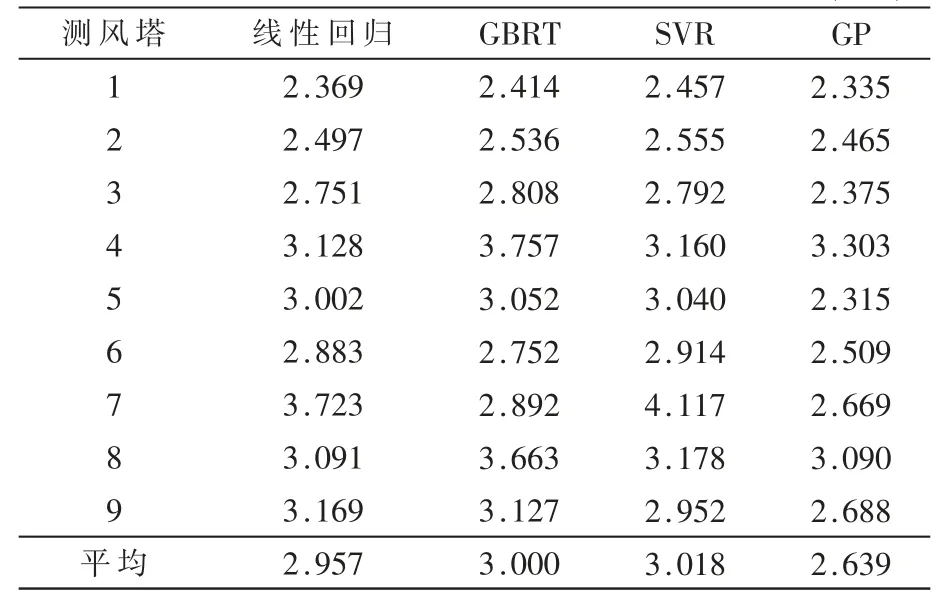
表3 72 h 风速预测实验 (m/s)

从两组预测实验可以发现，除了测风塔4 和8 之外，高斯过程回归的预测误差是最低的。同时，高斯过程的性能非常稳定，即使在不是最优模型的观测站4 和8，与RMSE 最优模型的差距也不超过0.2 m/s。

5 风速预测重构实验

5.1 长间距风速重构实验

长间距代表区域内不同观测点的距离为几十千米，第4 节用于单点预测实验的9 个测风塔相互间的距离在10～60 km。本文使用DBN 来重构误差最低的高斯过程回归预测结果，并比较重构前后风速预测情况的变化，如表4 所示。

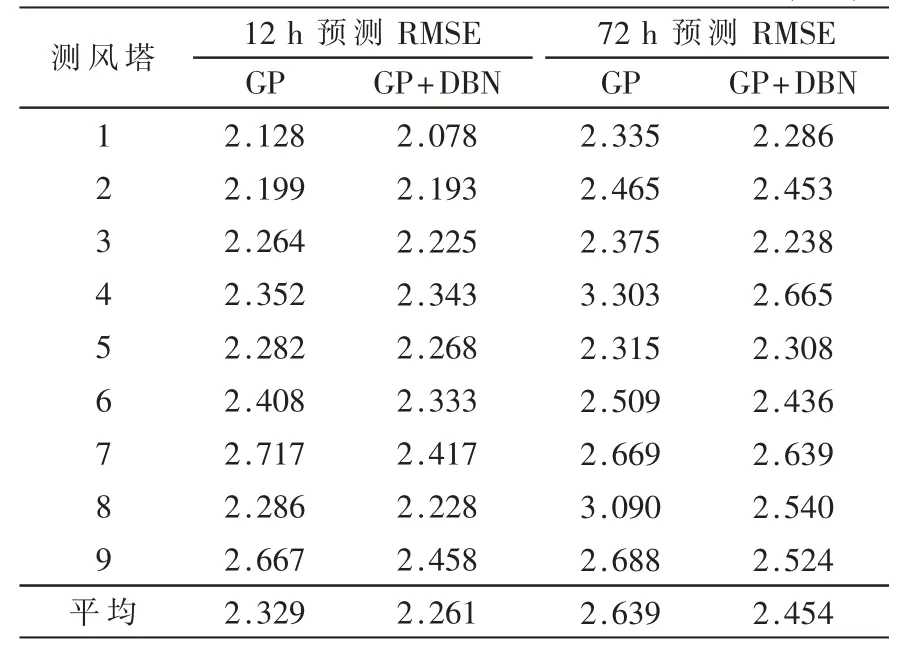
表4 长间距风速重构结果 (m/s)

从表4 中可以看到，尽管9 个观测站平均改善不大，12 h 预测误差降低0.068 m/s，72 h 预测误差降低0.185 m/s，但DBN 重构后所有测风塔的预测都优于GP的预测结果，说明DBN 重构非常稳定且没有损失。此外，在测风塔7 的12 h 预测、测风塔4 和8 的72 h 预测上，DBN 重构后的结果都有相当明显的改善，最大改善达到了0.55 m/s。这些测风塔的预测误差明显高于其他测风塔，但经过DBN 重构修正，预测误差降到了平均水准，说明DBN 对较差的预测结果有更为明显的改善。

图3 展示了测风塔8 的72 h 预测结果在DBN 重构前后的变化情况。图3 的两条曲线分别是GP 的预测误差和DBN 重构预测误差的天平均，可以看到在大多数误差较大的时段，DBN 重构后的预测误差显著低于GP 预测误差。DBN 重构GP 测风塔风速预测结果的实验结果表明，DBN 能够从数据中学习几十公里间距的风速相关性特征，并利用学习到的信息和特征来改善整个区域的风速预测结果，对原预测比较差的情况改善尤为明显。

图3 DBN 重构前后风速误差曲线

5.2 短间距风速重构实验

相比于长距离的空间相关性，短距离(小于10 km)的空间特性主要出现在相同风电场的不同风机之间。风机的间隔一般小于5 km，由于风机的运转也会对风速产生影响，即众所周知的尾流影响，因而短间距的风速空间特性更为复杂。本文选取国内某个风场进行风速预测重构实验，该风场包括49 个风机，风机间隔1～5 km，每台风机每隔6 min 记录一次风速和风电功率，时间长度为1 年。选取前80%时间的记录作为训练数据，使用其余20%来验证DBN 对风速预测的改善能力。

从图4 可以看到，49 个风机的风速预测经过DBN重构后均得到了改善，改善幅度为0.1～0.7 m/s，大多数风机的风速预测结果改善了0.4 m/s。这一结果从空间角度验证了DBN 的改善效果。

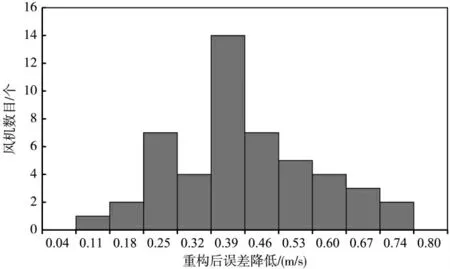
图4 风场内不同风机风速预测改善情况统计

图5 展示了经过DBN 重构后，每天风场所有风机平均风速的预测误差的变化情况，图5 中标记点为预测误差的日平均变化，即errorAfterDBN-errorBeforeDBN。从图5 中可以看出，风场总平均风速改善的天数超过了总天数的一半以上，同时在某些时期改善幅度非常大，例如第2、6、19和29 天，风场平均风速误差下降了约2 m/s。整体来看，长期上DBN 对于风速预测的改善也很明显。

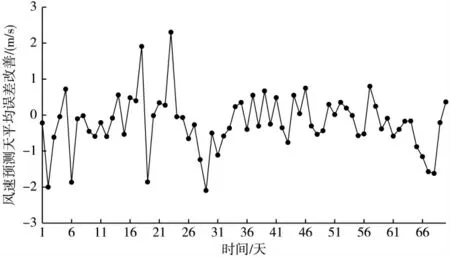
图5 DBN 重构后风场平均风速预测误差改善情况

图6 中的两条曲线分别代表风场总平均风速GP 预测和DBN 重构后的天平均误差。从图6 中可以看出，第18 和23 天的单点预测误差是很低的，经过DBN 后上升到3 m/s，处于平均水平。而单点预测误差很差的第3、9、29 天和误差高于4 m/s 的天中，DBN 重构后误差都有了明显下降，第29 天的预测误差从8 m/s 下降到6 m/s。因此，虽然在预测误差很低的情况下DBN 可能导致预测误差上升，但可以极大改善风速预测误差很大的情况，有利于提高风速预测的稳定性。整体来看，DBN 对风速预测误差呈现明显的改善效果。

图6 风场总平均风速预测误差变化

本实验中，风机的运转使得风的空间特性更加复杂，但DBN 通过数据依然能够捕捉到相关规律，进而优化单点预测的结果，平均改善幅度达到0.4 m/s。相比5.1 节长间距情况下平均改善0.185 m/s 的结果，说明距离越近，风速的空间内在规律和约束程度越强，DBN 的优化潜力也越大。

6 结论

本文比较了目前主流的单点风速预测算法，分析了它们的不足之处，进一步提出了利用深度置信网络学习风速的空间特性规律和约束来改善风速预测结果的方法。通过实验和分析，主要结论如下：

(1)基于单点的风速预测模型中，高斯过程(GP)的预测误差最低，并且预测性能稳定，在所有单点预测试验中均表现优异；

(2)DBN 能够充分学习和挖掘风速的空间分布规律和相关性特征，并且适用于不同间距(1～60 km)的情况；

(3)DBN 能够利用学习到的规律重构和改善风速预测，重构后的每个地点的预测误差最大降低0.7 m/s，平均降低0.4 m/s；

(4)DBN 对于预测比较差的情况改善尤为明显，改善幅度甚至可以达到2 m/s，这对于提高风速预测的稳定性有着重要的意义；

(5)DBN 在改善一些地点的预测的时候并不会增加其他地点的预测误差；

(6)DBN 存在降低高质量单点预测精度的现象，这可能源于多点风速预测误差的不一致，改进方案值得进一步深入研究。