基于改进AHP-熵权法的雷达装备可靠性评估指标赋权方法*

翟芸，胡冰，施端阳，3

（1.空军预警学院，湖北 武汉 430019；2.武警天津总队执勤第三支队，天津 300450；3.中国人民解放军95174 部队，湖北 武汉 430040）

0 引言

雷达装备可靠性是指雷达装备在规定的条件下和时间内完成规定功能的能力［1］。雷达装备的可靠性与雷达装备整个寿命周期的全部可靠性活动有关，是为了达到雷达装备的可靠性要求而进行的有关可靠性分析、试验和生产使用等一系列工作的综合作用的结果［2］。对雷达装备的可靠性进行研究，提出并建立科学合理的雷达装备可靠性评估指标体系，利用有效的可靠性评估方法，对雷达装备可靠性进行综合准确的评估，既有利于雷达作战效能的发挥，又可以倒逼设计厂家进一步提高雷达整机的可靠性水平。

目前，众多学者先后采用了各类方法对装备的可靠性进行了评估。在装备可靠性评估指标构建方面，文献［3］着眼于军用车辆的特点，建立了可靠性、维修性与保障性参数体系；文献［4］在调研的基础上，按照科学性、系统性、适用性、可比性的原则，建立了民用飞机可靠性参数体系；文献［5］基于目标问题度量（goal-question-metric，GQM）方法，建立了装备软件可靠性参数体系；文献［6］从软件可靠性定义入手，建立了航空装备的软件可靠性参数体系。

在对装备可靠性评估方法的应用上，文献［7］采用故障树建模分析与贝叶斯网络相结合的方法，对雷达伺服系统随动失效模式开展了可靠性分析；文献［8］引入模糊集合分解定理，建立了参数估计模型，对雷达电路板进行了可靠性分析；文献［9］将失效模式影响及危害度分析法（failure mode effects and criticality analysis，FMECA）与神经网络相结合，对某型雷达系统进行了可靠性分析；文献［10］提出了一种基于改进模糊层次分析法（fuzzy analytic hierarchy process，FAHP）和云模型的评价方法，针对雷达装备的软件可靠性进行了评估。

现阶段，对于装备可靠性评估指标的构建，大多集中在飞机、车辆和电子设备上，对于雷达装备的可靠性指标研究较少，且大都侧重于对部分结构的研究，很少有学者对于雷达整机的可靠性进行研究评估。

本文提出了一种改进层次分析法（analytic hierarchy process，AHP）-熵权法组合赋权的方法，对雷达装备的可靠性进行评估。首先，根据雷达装备的特点，构建了定性指标与定量指标相结合的雷达装备可靠性指标体系；然后采用改进的AHP 方法确定各评价指标的主观权重，并利用熵权法求得指标的客观权重；最后，利用最小二乘法对权重进行耦合，采用拉格朗日法求解该模型，得到各指标的组合权重，有效避免了用单一方法确定可靠性指标权重的局限性问题。通过实例分析，验证了该方法在对雷达装备进行可靠性指标进行赋权时的准确性和可行性。

1 雷达装备可靠性评估指标体系构建

根据《GJB 451A-2005.可靠性维修性保障性术语》［1］中对可靠性参数的分类、《GB/T 16260-2006.软件工程产品质量》［11］中对软件可靠性指标的度量要求、以及对装备可靠性设计的要求，根据雷达装备的结构和任务特点，按照科学性、系统性、完备性、独立性等要求，依据雷达装备可靠性的定义，结合雷达装备可靠性的相关要求，本文构建了如图1所示的雷达装备可靠性评估指标体系。

图1 雷达装备可靠性评估指标体系Fig.1 Radar equipment reliability evaluation index system

该指标体系主要将雷达装备可靠性评估指标体系分为5 个部分：

（1）雷达装备基本可靠性参数，主要包括故障率、平均故障间隔时间、平均维修间隔时间、平均修复时间、储存可靠度等反映雷达装备对维修人力要求的参数。

（2）雷达装备任务可靠性参数，主要包括平均严重故障间隔时间、任务可靠度、战备完好率等反映雷达装备在规定的任务剖面内完成规定功能能力的参数。

（3）雷达装备耐久性参数，主要包括可靠寿命、储存寿命、使用寿命、总寿命、首次大修期限等反映雷达装备在规定的使用、储存与维修条件下，达到极限状态之前，完成规定功能能力的参数。

（4）雷达装备可靠性设计参数，主要包括冗余设计、降额设计、耐环境设计、简单化和标准化、失效安全设计情况、人机工程等在雷达装备的研究和设计中，技术人员应该考虑设计的，可以使雷达装备达到可靠性指标的一系列设计参数。

（5）雷达装备软件可靠性参数，主要包括成熟性、容错性、易恢复性、可靠性的依从性等衡量雷达装备在规定的条件下和规定的时间内，软件不引起系统故障能力的参数。

2 基于改进AHP-熵权法的指标权重确定

2.1 基于改进AHP 的主观权重计算

层次分析法（AHP）是由美国运筹学家T.L.Satty［12］教授提出的，用AHP 分 析问题时，一般采用1～9 标度法，但在实际应用中，传统的1～9 标度法存在着一些缺陷，例如，一致性与权重拟合度较差、矩阵容量较小等［13］。基于此，国内外专家学者提出了0～2 标度、1～5 标度、x2［14］标度、指数标度法［15］等方法，本文根据各类标度法的优缺点，提出了一种1～9标度法与e0/4～e8/4标度法相结合的方式，在利用2 种标度法分别求出权重并且通过一致性检验的基础上，对其进行算术平均求值，合理利用2 种标度法的优缺点，使权重值更加可靠。

运用改进AHP 法确定雷达装备可靠性指标权重的步骤如下：

Step 1 建立对雷达装备可靠性影响因素的递进层次结构模型。确立其目标层、准则层以及方案层，规定下层因素影响上层因素，且相同层级之间的因素相互独立，在不影响整体评价结果的基础上，每一层中的因素应尽量减少。

Step 2 构造判断矩阵。假设评估对象R受某指标层n个因素{a1，a2，…，an}的影响，分别按照1～9 标度法及e0/4～e8/4标度法，将ai和aj(i≠j)对评估对象R的相对重要程度用数字表现出来，分别记为aij和aji，根据判断矩 阵的构造，aij和aji应该满足：aij＞0，aji＞0，aij=1/aji，aii=1，i≠j.

由此可以得到由相对属性构成的判断矩阵A=，判断矩阵标度及含义如表1 所示。

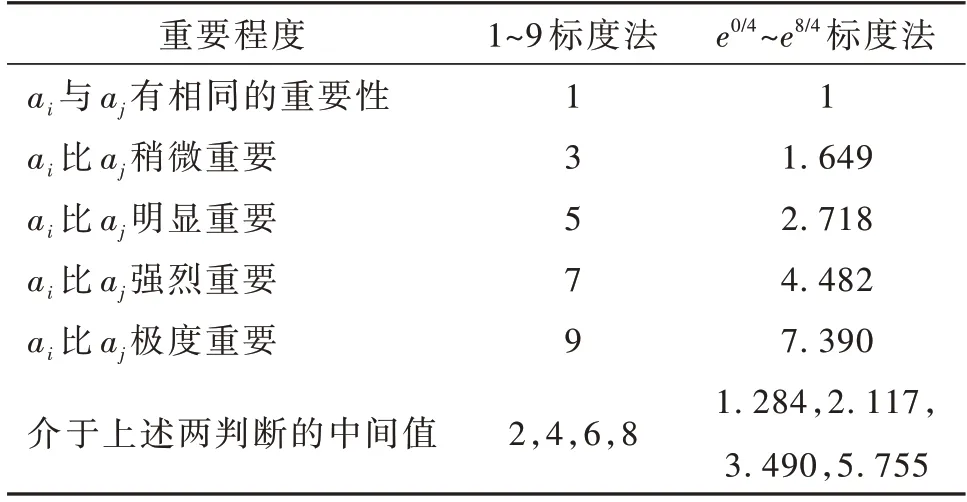
表1 2 种判断矩阵标度及其含义Table 1 Two kinds of judgment matrix scales and their meanings

Step 3 计算各因素权重。根据矩阵理论可知，各因素权重系数就是判断矩阵的特征向量w，可由下列公式求得：

一般来说，计算特征向量一般采用方根法、幂法、算数平均法、几何平均法等，本文采用方根法计算指标的权重系数，具体步骤如下：

得到的矩阵W=(w1，w2，…，wn)T即为判断矩阵的特征向量，即为各指标的权重系数。

（4）计算判断矩阵的最大特征值

式中：(AW)i为AW的第i个分量。

Step 4 对判断矩阵进行一致性检验。由于对于指标的重要度比较存在主观性，所以需要对判断矩阵进行一致性检验。检验步骤如下：

（1）计算一致性指标

（2）计算一致性比率

式中：RI为平均随机一致性指标，其值可以通过表2获得。当CR越小时，判断矩阵的一致性就越好，当CR＜0.1 时，可以认为判断矩阵的差异在允许范围内，具有一致性。

表2 平均随机一致性指标取值表Table 2 Average random consistency index value table

Step 5 得到组合权重向量。通过加权融合主观权重W1，W2，获得组合权重向量W。其中，W=，W1为利用1～9 标度法求出的权重值，W2为利用e0/4～e8/4标度法求出的权重值。

2.2 基于熵权法的客观权重计算

熵的概念来源于热力学，可以用来度量系统的无序程度，可以用来表示已知数据包含的信息量，并确定其权重［16］。当评价指标值相差越大时，熵值越小，则该指标携带的信息量较大，可以对其赋予较大的权重，反之，指标携带的信息量较少。

运用熵权法确定雷达装备可靠性指标权重的步骤如下：

Step 1 对数据进行标准化处理。设矩阵X=(xij)n×m，(i=1，2，…，n；j=1，2…，m) 为 由n个 被评估对象，m个评价指标构成的原始数据矩阵。对不同类型的数据按照如下公式实施标准化处理，

式中：yij为第j个评价指标，在第i个评价对象上的标准化处理后数值，且yij∈[0，1]。

Step 2 对判断矩阵进行归一化。

Step 3 计算各评价指标的熵值。

行修正，各指标客观权重系数为

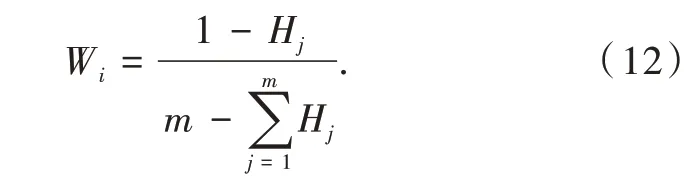
2.3 基于改进AHP-熵权法的组合权重计算

采用最小二乘法优化组合权重模型，对改进AHP-熵权法求得的主客观权重W，Wi进行耦合得到权重W*：

用拉格朗日法求解该模型，即可得到综合权重W*。其中，（bij）为具有m个评价指标，n个被评估对象标准化后的数据矩阵。

3 实例分析

以某型雷达的可靠性评估为例，根据图1 构建的雷达装备可靠性评估指标体系，对雷达装备可靠性指标进行组合赋权。

3.1 改进AHP 法确定评估指标的主观权重

邀请专家分别根据表1 所示的比例标度法，对图1 中的一级指标基本可靠性参数A1、任务可靠性参数A2、耐久性参数A3、可靠性设计参数A4、软件可靠性参数A5按顺序进行两两比较，分别得到1～9 标度法以及e0/4～e8/4标度法所对应的判断矩阵A，A*：

同理，得出A1所属的5 个二级指标所对应的判断矩阵B1，B1*；A2所属的3 个二级指标所对应的判断矩阵B2，B2*；A3所属的5 个二级指标所对应的判断矩阵B3，B3*；A4所属的6 个二级指标所对应的判断矩阵B4，B4*；A5所属的4 个二级指标所对应的判断矩阵B5，B5*：

表3～8 为根 据1～9 标度法、e0/4～e8/4标度 法分别计算出的指标权重及其改进后的综合权重。根据公式（6）～（7）对判断矩阵进行一致性检验，结果表明各判断矩阵都具有一致性，则权重向量WA=（0.138 2，0.484 6，0.097 8，0.062 5，0.217 1）；=（0.258 0，0.421 6，0.153 2，0.089 9，0.077 4）；=（0.257 4，0.579 6，0.163 1）；=（0.133 5，0.080 2，0.280 9，0.159 7，0.345 7）；=（0.348 4，0.178 8，0.297 1，0.050 2，0.082 5，0.043 1）；=（0.464 6，0.171 4，0.282 1，0.081 9）。

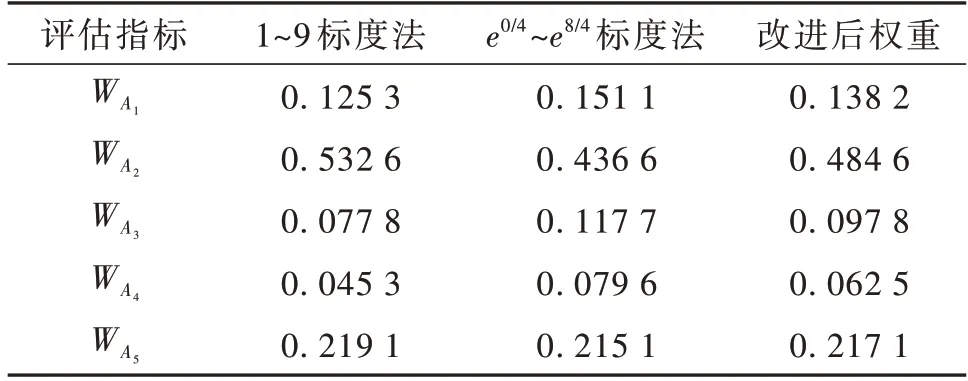
表3 改进AHP 评估指标权重表ITable 3 Improved AHP evaluation index weight table I

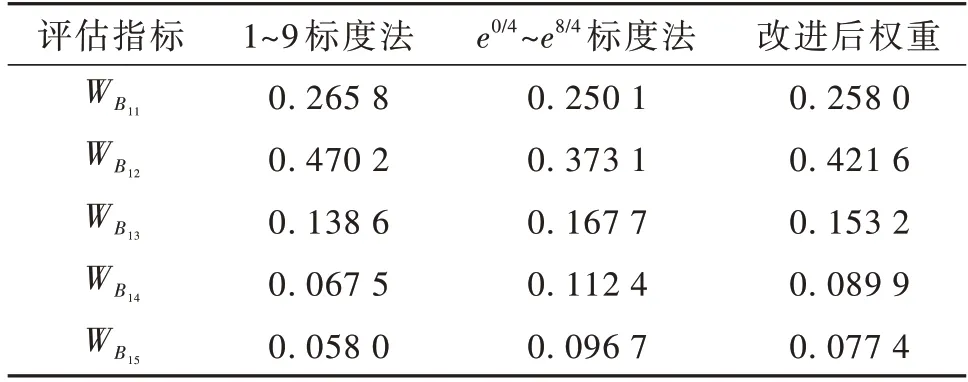
表4 改进AHP 评估指标权重表ⅡTable 4 Improved AHP evaluation index weight table Ⅱ

表5 改进AHP 评估指标权重表ⅢTable 5 Improved AHP evaluation index weight table Ⅲ

表6 改进AHP 评估指标权重表ⅣTable 6 Improved AHP evaluation index weight table Ⅳ

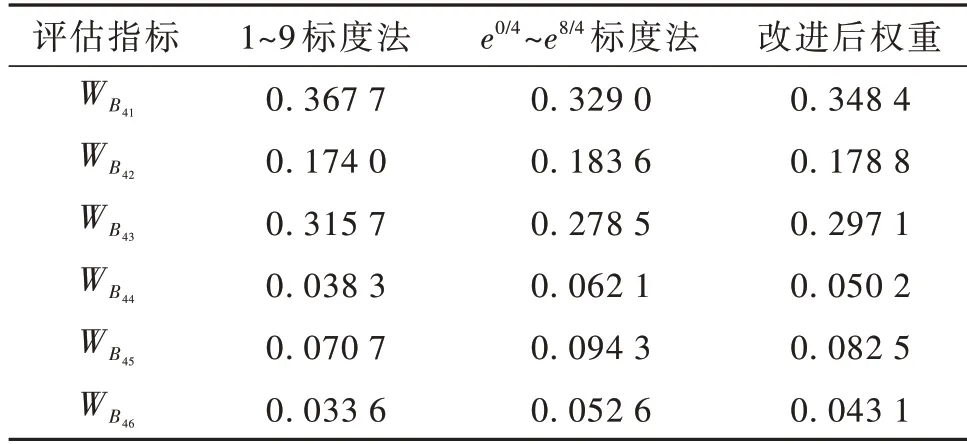
表7 改进AHP 评估指标权重ⅤTable 7 Improved AHP evaluation index weight table Ⅴ

表8 改进AHP 评估指标权重ⅥTable 8 Improved AHP evaluation index weight table Ⅵ

可以得到，基于改进AHP 赋权法的各底层指标相对于雷达装备可靠性的主观权重W=（0.035 6，0.058 2，0.021 1，0.012 4，0.010 7，0.124 7，0.280 9，0.079 0，0.013 1，0.007 8，0.027 5，0.015 6，0.033 8，0.021 8，0.011 2，0.018 6，0.003 1，0.005 2，0.002 7，0.100 9，0.037 2，0.061 2，0.017 8）。

3.2 熵权法确定评估指标的客观权重

根据公式（10）对采集到的雷达装备可靠性原始数据矩阵进行处理，得到归一化后的矩阵：

利用公式（11）～（12）计算各指标基于熵权法相对于雷达装备可靠性的客观权重值Wi=（0.032 2，0.040 5，0.032 2，0.034 9，0.032 1，0.034 9，0.034 9，0.082 6，0.048 9，0.033 0，0.031 4，0.040 5，0.034 9，0.034 9，0.032 2，0.032 3，0.032 1，0.082 6，0.034 9，0.032 2，0.082 6，0.040 5，0.082 6）。

3.3 确定评估指标的综合权重

根据公式（13）得到各指标相对于雷达装备可靠性的综合权重值W*=（0.033 9，0.049 4，0.026 7，0.023 6，0.021 4，0.079 8，0.157 9，0.080 8，0.031 0，0.020 4，0.029 5，0.028 1，0.034 3，0.028 3，0.021 7，0.025 4，0.017 6，0.043 9，0.018 8，0.066 5，0.059 9，0.050 8，0.050 2）。

结合图1 的雷达装备可靠性评估体系，对比图2中的主观权重W、客观权重Wi以及综合权重W*，对不同方法得到的指标权重进行灵敏度分析。可以看出，不同赋权方法得到的“平均故障间隔时间”、“任务可靠度”、“简单化和标准化”、“失效安全设计情况”、“成熟性”这5 个指标的敏感性差别较大。具体表现在，采用改进的AHP 方法进行赋权时，“平均故障间隔时间”、“任务可靠度”2 个指标的敏感性较高，这主要是因为专家在进行比较时，只注意了指标的重要性，忽略了技术成熟等原因使雷达装备故障率较低的现实情况，从而赋予了这2 个指标较大的敏感性。另外，在根据客观数据采用熵权法进行赋权时，得到的“简单化和标准化”、“失效安全设计情况”、“成熟性”这3 个指标的敏感性较高，说明在雷达装备设计阶段所制定的设计参数及雷达装备软件成熟性情况，对雷达装备可靠性也存在着较大的影响，与专家的主观印象存在一定偏差。

图2 3 种方法所确定权重值对比折线图Fig.2 Comparison of weight values determined by the three methods

根据上述分析可得，采用主客观赋权法得到的权重值，有效弥补了主观方法过于依赖专家经验，客观方法仅仅考虑数据实际的缺陷，使得到的雷达装备可靠性指标权重值更加科学合理。

4 结束语

本文主要构建了包括基本可靠性参数、任务可靠性参数、耐久性参数、可靠性设计参数、软件可靠性参数在内的雷达装备可靠性评估指标体系；对传统的AHP 赋权方法进行了改进；运用改进后的AHP和熵权法对指标进行主客观组合赋权，提出了改进的AHP-熵权法综合赋权方法。通过实例，验证了该方法能弥补单一赋权法的不足，使赋权结果更加科学合理。