基于地基激光雷达数据的落叶松人工林削度方程构建

邹茂胜，孙毓蔓，李丹丹，贾炜玮，王璐瑶

（东北林业大学 a.林学院；b.森林生态系统可持续经营教育部重点实验室，黑龙江 哈尔滨 150040）

落叶松具有天然分布广、速生、材质好、抗性强和适应性广等特点[1]，成为我国主要的针叶用材树种之一，因此，其立木材积的准确估计和林分蓄积量的计算对于林场的经营管理与决策尤为重要。传统方式主要是通过砍伐树木来获取解析木干形数据来建立削度方程求算材积，或者通过编制好的立木材积表计算材积。这就需要花费大量的人力与物力，而且在集约经营采伐受限的条件下，通过伐倒木来获取数据变得困难。近年来，地基激光雷达在林业调查中的广泛应用，很大程度上改变了传统的野外调查方法，提高了对森林定性分析和定量反演的性能，推动精准林业和数字林业的发展。

近些年来，地基激光雷达（TLS）在森林资源调查中广泛应用，森林参数的获取、林分因子调查和森林蓄积量估测变得更加高效。杨玉泽等[2]依据地面三维激光扫描获取白桦的点云数据建立树干削度方程，与解析木数据建立的削度方程对比，模型拟合效果排序一致，而且具有较高的拟合精度，但用于构建削度方程的直径数据只提取到树干6 m 处，而树干上部的直径未涉及到；熊妮娜等[3]以山杨树为例，依据地基激光雷达获取的数据求算立木材积，以全站仪活立木材积测量值作为真值进行比较，结果表明，两者精度十分接近，且存在显著相关性；但其未对不同高度处直径提取精度进行比较分析，同时全站仪与解析木干形数据获取的材积存在5%以内的误差[4-5]。花伟成等[6]利用TLS 数据建立杨树削度方程并进行立木材积估算，与二元材积方程估计结果在统计上无显著差异，为人工林的蓄积量调查提供了有效的技术支持，但研究样本量较少，进行推广还不具有很强的说服力。

与传统模型相比，加入随机效应后的混合模型能提高模型拟合效果，其随机效应的方差和协方差矩阵可以反映树木间变化[7]和数据间的相关性和异质性[8]，因此混合模型广泛应用于林分生长模型中[9-10]。陈哲夫等、姜立春等[10-11]通过非线性混合模型拟合落叶松树干削度模型，结果表明，考虑树木效应的混合模型比考虑样地效应的模型精度更高，而且混合模型通过校正随机参数值能提高模型预测精度。张森森[12]根据构建的杉木最优基础削度方程，建立基于样地效应、样木效应和嵌套两水平效应的混合模型，发现基于样木效应的Kozak-2004 混合模型拟合精度最好，而且能有效消除数据间的自相关性。然而，以上研究大多数据量小，并且借助TLS 数据构建削度方程时未对其不同高度处直径进行大量数据验证。本研究通过皆伐样地的落叶松实测了大量树干直径数据，对TLS 提取落叶松人工林不同高度处的直径精度进行分析，在满足一定提取精度的情况下，利用TLS 提取不同高度处的直径构建基于混合效应的削度方程来反映树干干形变化，为编制出材率表做准备。

本研究以黑龙江省佳木斯孟家岗林场的落叶松人工林Larix olgensis为研究对象，使用地基激光雷达获取样地点云数据，首先使用LiDAR360软件对点云数据进行处理并提取相对高处直径数据，再将提取数据与实测数据进行对比验证，探究TLS 获取数据的可行性；然后利用点云数据提取的相对高处直径数据构建落叶松树干削度方程，选出基于TLS 的落叶松人工林最优削度方程；最后，为进一步提高模型的预测精度引入了随机效应，建立基于树木效应的非线性混合模型，以期为落叶松人工林的材积监测和评估提供高效测量方法，为精细化合理造材提供理论支持。

1 研究区域与数据处理

1.1 研究区域概况

研究区为黑龙江省佳木斯市桦南县孟家岗林场（130°32'～130°52'E，46°20'～46°30'N），气候属东亚大陆性季风气候，年平均气温2.7℃，年平均降水量550 mm，地势东北高而西南低，地貌以低山丘陵为主，坡度较为平缓。孟家岗林场是以针叶树为主的人工林用材基地，主要是落叶松、红松Pinus koraiensis、樟子松Pinus sylvestris，其中落叶松占人工林面积60%。

1.2 数据获取

样地的选取是林场根据经营要求，在每一小班内划定1 块样地进行皆伐设计，共8 块样地。表1为样地基本情况。

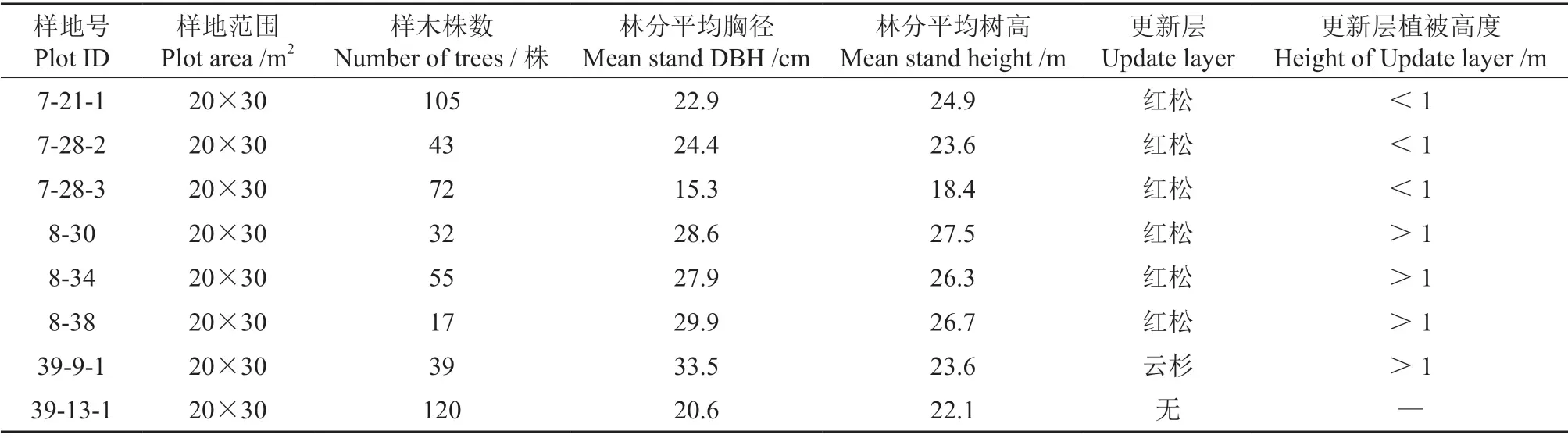
表1 样地概况Table 1 The basic information of sample plots

2020年10月进行数据采集，首先在样地内进行每木检尺和相对坐标定位，获取胸径、树高、活枝高、冠幅等因子。其次对样地进行TLS 扫描，使用Trimble TX8 三维激光扫描仪获取点云数据，在样地内均匀布设站点，每块样地至少扫描5 站，根据林地林下状况和样地内单木位置状况，适当增加扫描站点数，以获取更加完整的样木信息；在样地周围布置10 个靶球，保证每次仪器能扫描到5～6 个靶球，以便后期点云数据拼接；最后，对皆伐后的样地进行单木相对高处直径测量（包括全树高的0 m、0.02h、0.04h、0.06h、0.08h、0.1h、0.2h、0.25h、0.3h、0.4h、0.5h、0.6h、0.7h、0.75h、0.8h、0.9h处直径），皆伐后，倒木排列不规整，导致测量时存在很大困难，因此共收集了202 株样木的相对高处直径数据。

1.3 数据处理

将TLS 获取的数据导入Trimble RealWorks 软件中进行站点拼接，采用单点配准的方式进行配准，最后将全部站点拼接成一块完整的样地点云数据，然后以las1.4 软件格式输出。将经过配准的点云数据导入Lidar360 软件进行预处理，主要包括去噪、重采样、地面点滤波分类、提取数字高程模型、归一化、点云分割、坐标匹配。经过预处理后，得到一个包含树高、胸径、冠幅、单木位置等信息的文本文件，剔除异常值后，得到单木的相对位置图。基于本研究样地为落叶松人工纯林，而且林分稀疏，所以采用人工目视解译方法进行匹配，如图1所示。

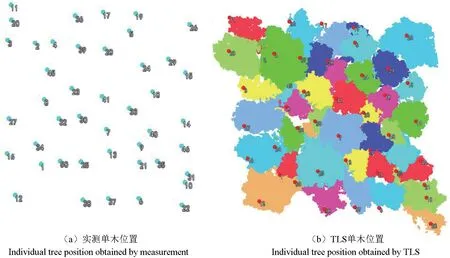
图1 单木位置匹配Fig.1 Position matching for individual trees

2 研究方法

2.1 TLS 单木参数提取和精度评价

本研究将单木点云最高处的Z值作为树高，如图2a 所示，树高为25.35 m。目前，胸径的提取方法主要是基于Hough 变换算法[13]和最小二乘法[14]。依据LiDAR360 软件的TLS 种子点编辑工具，研究选取切片厚度0.2 m，胸径横切片选择1.2～1.4 m 之间的点云数据，并通过拟合圆（基于最小二乘法）的方法提取DBH 值，图2d 为拟合结果，1 表示ID 号，0.255 5 为拟合得到的胸径值，单位为m。树干各相对高直径提取位置如图2b 所示，相对高处直径的提取方法与胸径相同。采用决定系数（R2）、均方根误差（RMSE）、提取精度（p）进行TLS 数据提取的树高、胸径和相对高处直径的精度评价。

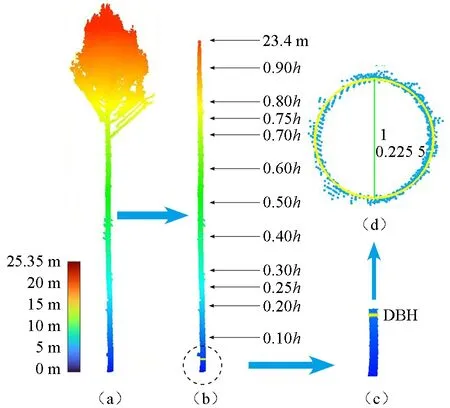
图2 相对高和胸径拟合Fig.2 Fitting of relative height and breast diameter

2.2 模型构建

2.2.1 基础削度方程选择

基于以往学者对东北林区落叶松人工林干形削度方程的研究[11,15-17]，本研究选取以下方程（表2）作为本研究的基础模型，其中简单削度方程3 个，可变参数削度方程6 个。可变参数削度方程能准确模拟不同树干以及不同高度的干形变化，提高对森林蓄积的预测精度，但参数过多，也导致模型复杂。

表2 基础模型†Table 2 Basic model

2.2.2 模型评价和选择

利用R 语言的sample 函数将TLS 提取的全部数据，按照3∶1 的比例分为建模数据和检验数据，如表3所示。

表3 模型特征统计Table 3 Characteristic statistics of models

使用R 语言的nls 函数对数据进行非线性拟合得到参数估计值，采用相关系数（R2）、均方根误差（RMSE）和平均误差（Bias）作为模型拟合程度的度量，从而筛选出最优削度方程。其中，模型的R2越大，RMSE 和Bias 越小，说明模型的拟合效果越好。采用R2、RMSE、相对百分误差（MAPE）、Bias 和预估精度（p）指标对基础削度方程进行独立性检验。

2.2.3 非线性混合效应模型

混合效应模型可同时对树木间和样地间数据进行分析，分析时不需要假设数据中观察值的相互独立，可以修正因观察数据的非独立性引起的参数标准误差估计，因此广泛应用于林业中。将最优的削度方程加入随机效应，构建混合模型。根据张森森[12]和姜立春等[11]的研究，考虑树木效应的混合模型比考虑样地效应的精度更高，因此本研究探讨了基于树木效应的混合模型，混合模型的构建包括以下3 步：

1）确定参数效应。非线性混合效应模型包括固定参数和随机参数两部分，首先把方程中所有参数当作随机参数，将不同随机参数组合的模型进行拟合，用Akaike 信息准则（AIC）、贝叶斯信息准则（BIC）和对数似然值（-2Log Likelihood）检验模型的拟合优度，AIC、BIC和-2Log Likelihood(LL)指标越小表明拟合效果越好；利用似然比检验（LRT）和P值进行检验，当P值小于0.05 认为差异显著；当不显著时选择更少的参数拟合以避免过参数化。

2）确定树木内方差协方差结构（Ri）。为解决误差相关性和异方差问题，本研究采用一阶自回归模型AR(1)解决树木内的误差相关性。目前林业上基本采用式（1）来描述：

式（1）中：σ2指模型的残差方差值，GI为描述方差异质性的对角矩阵，Гi为树木内的相关性结构。

3）确定树木间方差协方差结构（D）。用广义正定矩阵来描述随机效应的方差协方差结构，解释样木间的可变性，以3 个随机参数的方差协方差结构为例，如式（2）

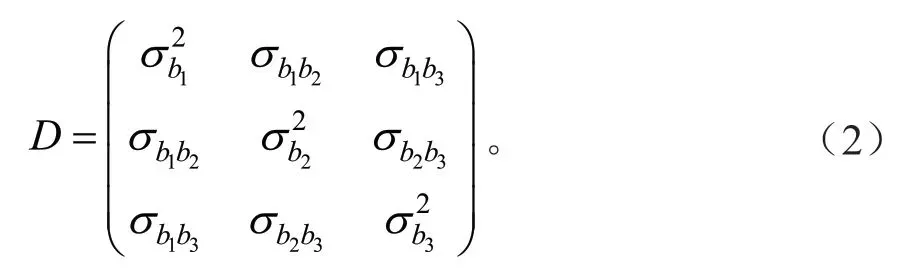
式（2）中：为随机参数b1的方差；为随机参数b2的方差；为随机参数b3的方差；为随机参数b1和b2的协方差；为随机参数b1和b3的协方差；为随机参数b2和b3的协方差。

随机效应部分的检验需要二次抽样来计算随机参数值[10]，本研究使用式（3）计算随机参数；选择RMSE、Bias 和预估精度（P）作为混合模型拟合评价指标，RMSE 和Bias 越小越好，P越大说明精度越高。

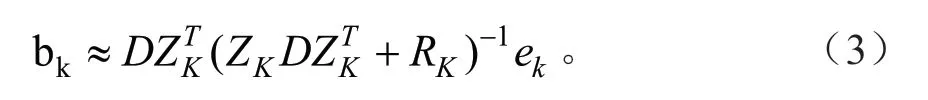
式（3）中：D为随机效应参数方差协方差矩阵；ZK为已知设计矩阵；RK为误差方差协方差矩阵；ek为误差向量。

3 结果与分析

3.1 TLS 提取数据精度分析

3.1.1 单木分割精度

经过实测数据坐标与TLS 获取的位置信息图匹配后可知，样地实测株数483 棵，与TLS 匹配成功461 棵，匹配精度95.45%。每块样地正确匹配结果如表4所示，其中，7-28-2 样地匹配精度最高达97.67%，其次是7-21-1 样地匹配精度为97.14%，匹配精度大于90%，小于97%的样地共4 块，最后8-30 和39-9-1 样地匹配精度均小于90%，因为样本量较小的关系；而且样地情况较为复杂，单木分割存在误分、错分和漏分的情况。树高和胸径的提取精度均大于95%，整体提取效果不错，胸径的提取精度均大于树高，由于样地内林木较高，离仪器较远，获取点云密度过低，对于树顶点判断错误，造成树高提取精度较低。

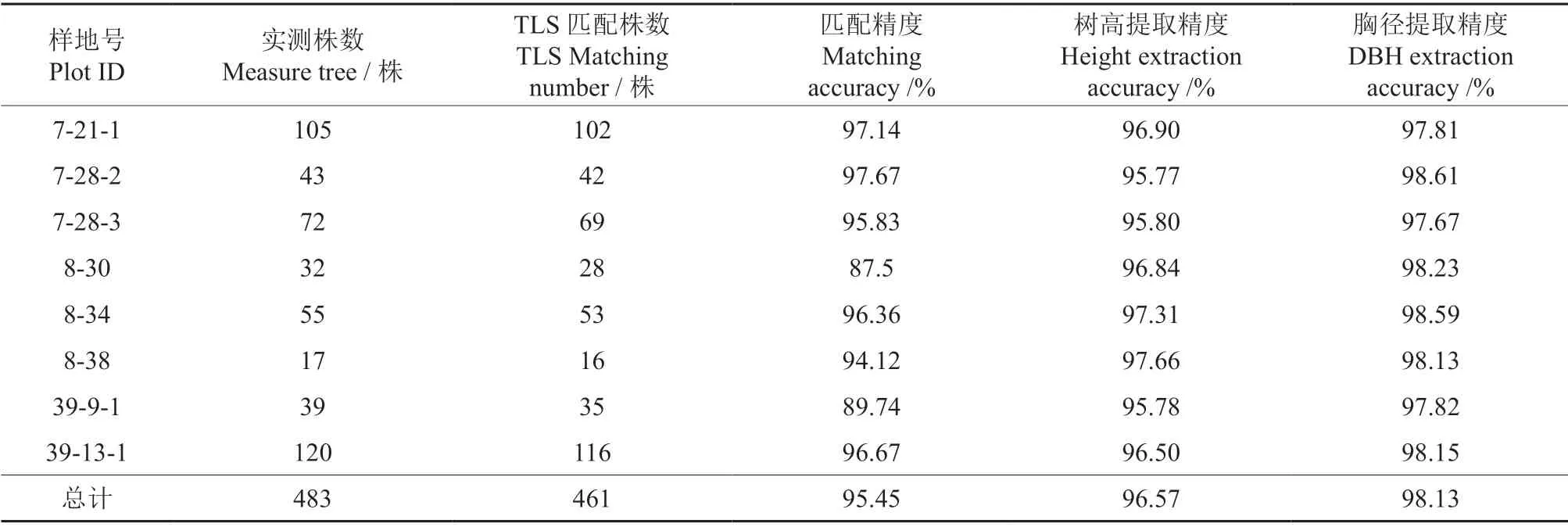
表4 单木分割结果Table 4 Single wood segmentation results

3.1.2 TLS 单木参数提取精度

将TLS 提取的数据与皆伐样地实测的202 棵树进行精度分析，结果如表5所示，0.06h精度最高达到98.07%，其0.06h处的实际高度与胸径处接近，与胸径整体提取精度仅相差0.06%；0 m 处直径的精度相对于0.02h、0.04h、0.06h等精度降低2～3 个百分点，随着树高的增加，提取精度逐渐降低；而R2先随着树高增大，到0.06h处达到最高R2=0.991 2，然后又逐渐减小；RMSE 值也表现出相似的结果，主要原因是部分样地林下更新植被遮挡，存在点云缺失；并且外业测量时发现大径阶样木0 m 处多为不规则的椭圆形，为此存在一定的误差，导致0 m 和0.02h、0.04h、0.06h处指标较低。0.8h指标低于90%，因为样地内落叶松树木较高（树高基本大于20 m），树冠较大，树顶距扫描仪的距离较远，因此TLS 扫描时样木上部树冠遮挡较为严重，树干上部点云缺失，导致0.8h及以上相对高处直径拟合结果变差或者拟合不出。对提取的胸径和树高与实测数据进行回归分析，从图3a 中能够看出，TLS 提取的胸径与实测胸径相关性达到0.99 以上；从图3b 中能够看出，TLS 提取的树高与实测树高相关性达到0.91以上，胸径的提取效果要好于树高。

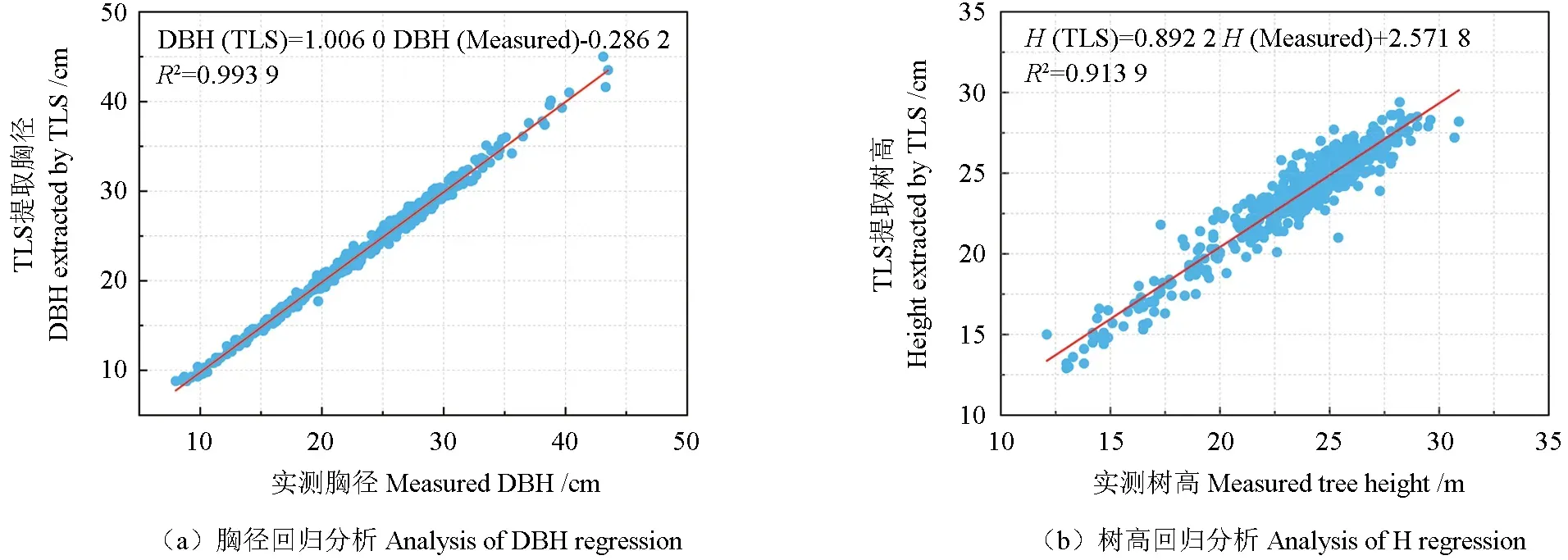
图3 树高、胸径回归分析Fig.3 Analysis of tree height and DBH

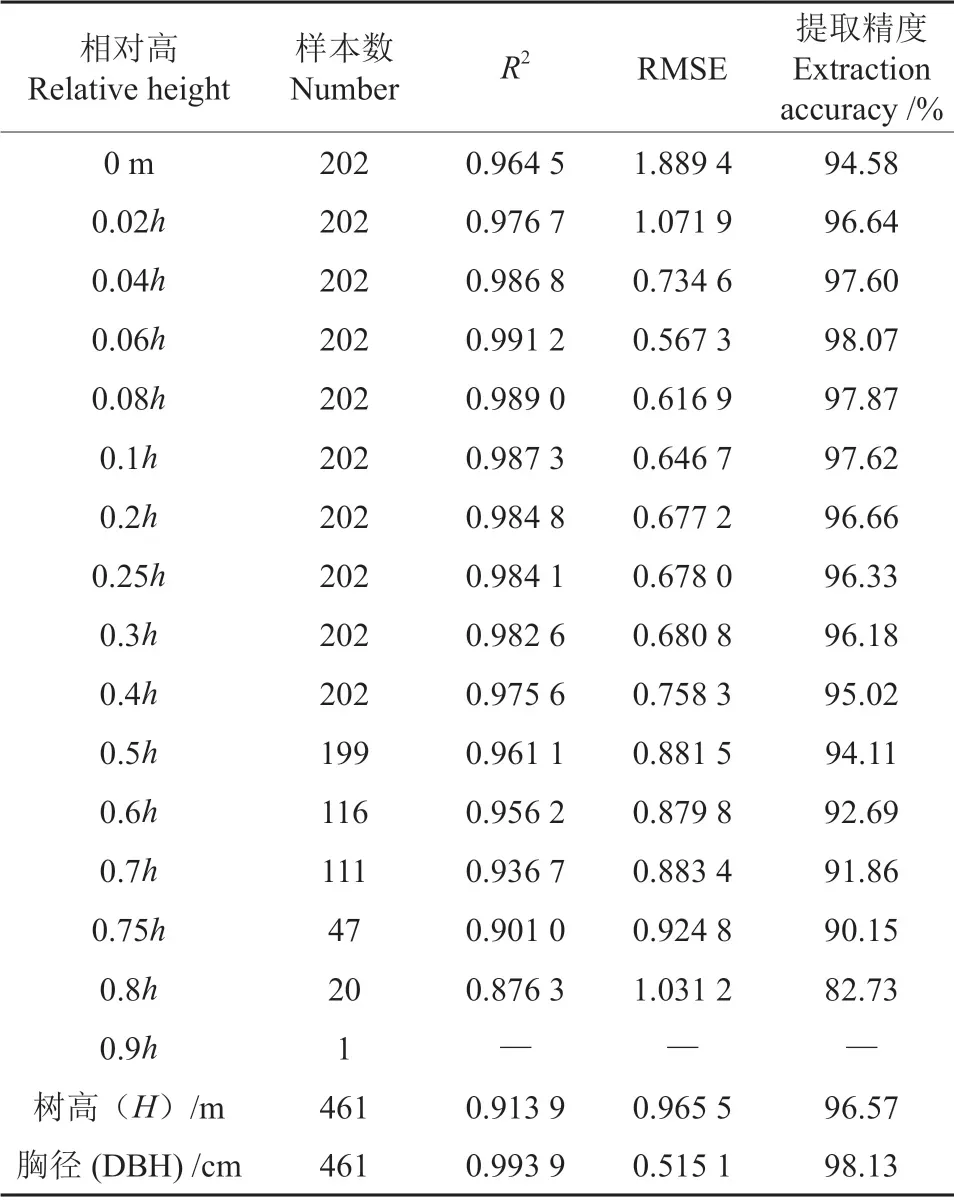
表5 树高、胸径和相对高处直径精度分析Table 5 Accuracy analysis table of tree height,DBH and relative height diameter

3.2 削度方程拟合与检验

经过3.1 节数据精度检验分析可得，TLS 提取的数据精度总体较高，而且显著相关，可以用于削度方程的构建。基于本研究所选的9个基础模型，根据表（6）模型拟合统计量可以看出，模型4的R2=0.978 3，RMES=1.179 9，拟合效果最好；其次，模型6 和模型9 拟合效果均不错；而模型2和3 拟合效果相对较差，R2小于90%，RMES 均大于2.5，Bias 大于6。综合模型评价指标，模型拟合效果为：模型4＞模型9＞模型6＞模型5＞模型7＞模型1；其中模型4（Kozak 1988）和模型9（Kozak 2004）拟合效果基本一致。

从表6看出模型预测能力与模型拟合效果一致，即模型预测效果为：模型4＞模型9＞模型6＞模型5＞模型7＞模型1＞模型8＞模型2＞模型3。为更加全面地评价模型的预测能力，图4绘制出各模型的残差图，模型4 和9 的残差分布较均匀，其余模型呈现出喇叭状，表现出明显的异方差。因此模型4 和模型9 的预测能力较好。

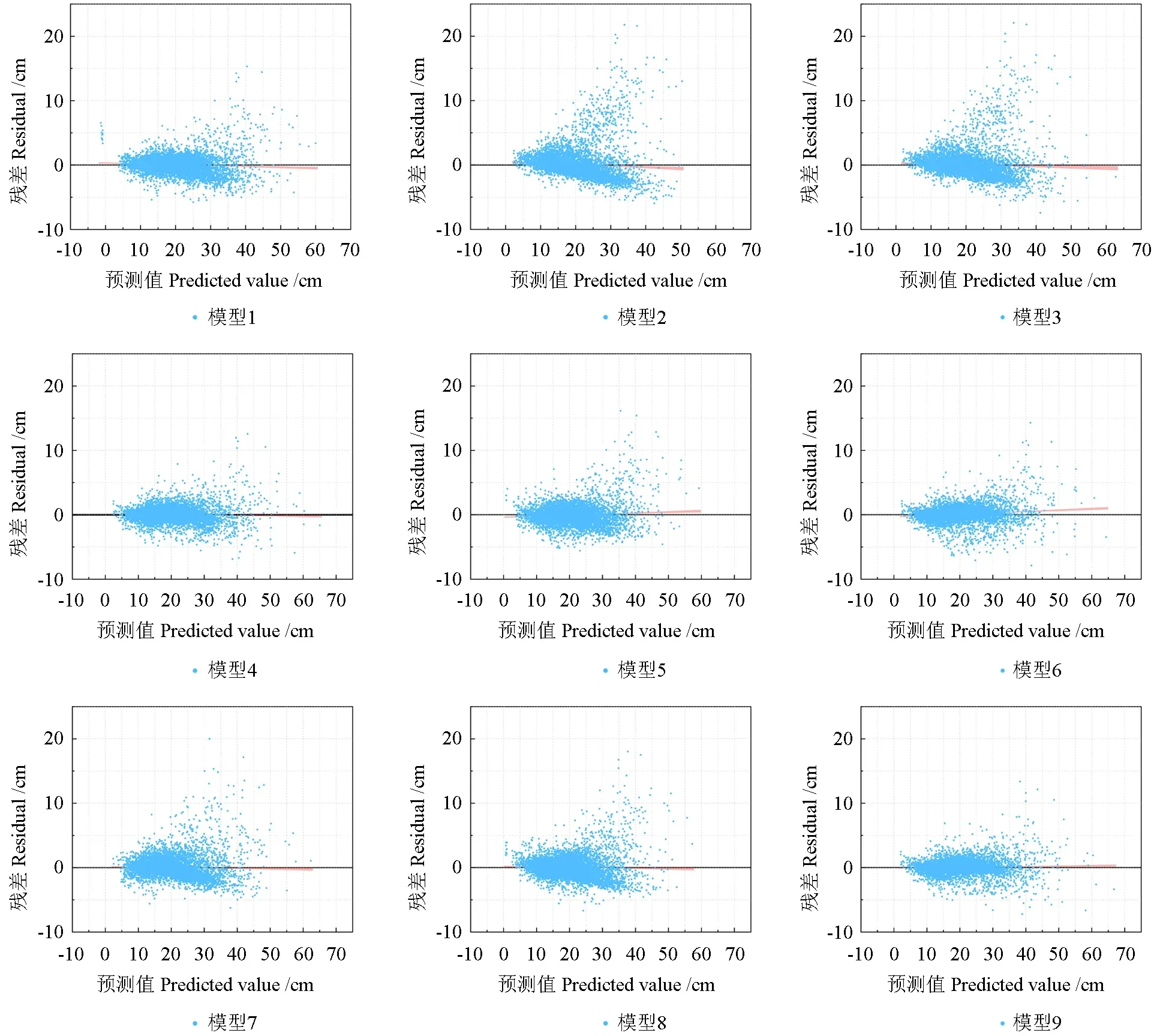
图4 基础模型残差图Fig.4 Residual diagram of the basic model

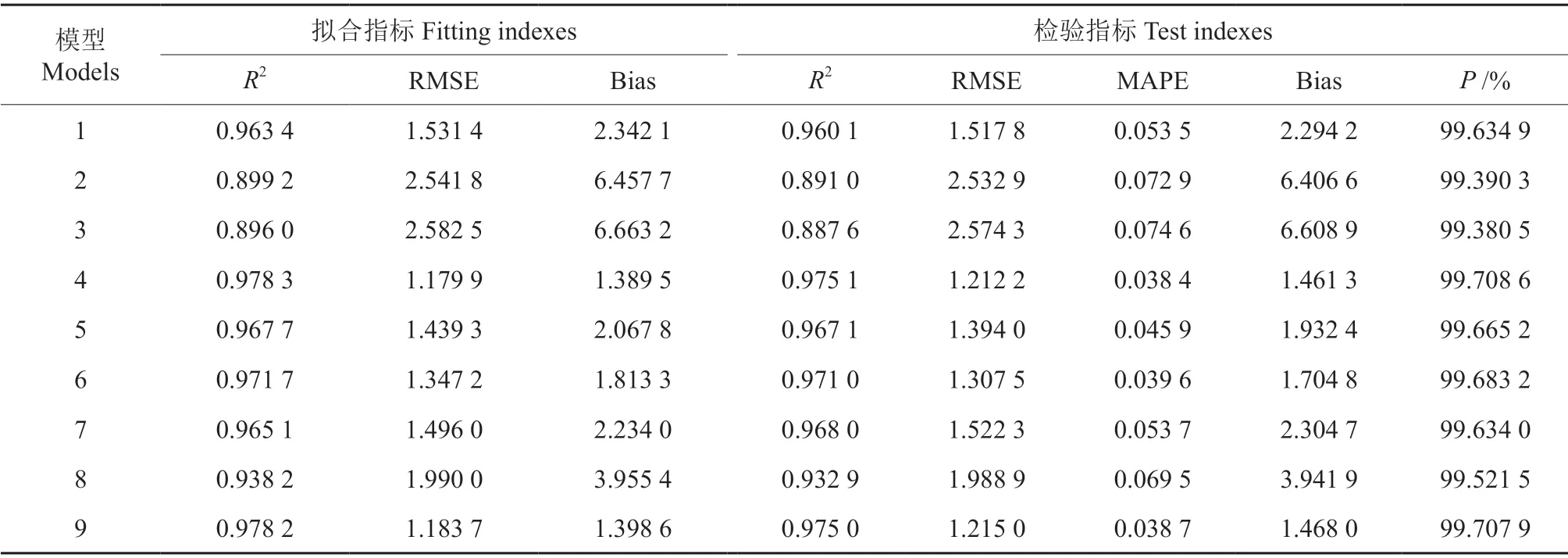
表6 模型拟合和检验指标Table 6 Model fitting and test indexes

3.3 基础模型预测分析

3.3.1 不同径阶模型检验

上述模型拟合与检验不能说明同样适用于不同径阶的树干削度模型，因此采用分径阶比较各模型在不同径阶下的预测精度变化，将检验数据按照8 cm 作为一个径阶进行划分，由于检验数据中径阶大于30 cm 的样本量相对较少，因此将检验数据划分为（6 cm ≤DBH＜14 cm）、（14 cm ≤DBH＜22 cm）、（22 cm ≤DBH＜30 cm）、（DBH ≥30 cm）4 组，基于上面结果，选择Kozak-1988、曾伟生模型和Kozak-2004进行分径阶段检验，利用上述拟合得到的参数估计值计算各模型的（MAPE）指标进行评价，因为MAPE不仅考虑预测值与真实值的误差，还考虑与真实值之间的比例，结果如图5a 所示：

由图5a 可知，6 cm ≤DBH＜14 cm 和14 cm ≤DBH＜22 cm 径阶段中Kozak-2004 的MAPE 值最小，曾伟生模型的MAPE 值最大；22 cm ≤DBH＜30 cm 径阶段Kozak-1988 的MAPE 值最小，曾伟生模型的MAPE 值最大；30 cm ≤DBH 径阶段下，曾伟生模型的MAPE 值最小，Kozak-2004的MAPE 值最大。虽然在不同径阶段下MAPE 最小值所对应的模型不同，但Koza-k1988 的MAPE值与不同模型下的最小MAPE 值相差不超过0.005，因此，在不同径阶下，Kozak-1988 模型对于孟家岗林场落叶松人工林干形预测表现良好。

3.3.2 模型分段检验

为分析Kozak-1988、曾伟生模型和Kozak-2004 在不同树高处直径预测效果，将相对高分为0.1h、0.2h、0.3h、0.4h、0.5h和0.6～0.9h共6 个段，由于地基激光雷达对树干上半部扫描受到树高和树冠间相互遮挡等影响，检验样本中相对高0.6h及以上树干点云缺失严重，许多单木由于树干点密度太小导致圆拟合直径误差较大，或者拟合不成功，因此将0.6h及以上部分作为1 个分段。用上述拟合的参数估计值计算模型的MAPE 指标，由图5b 可以看出，曾伟生模型的MAPE 值在0.1h和0.2h处，明显高于其他两个模型，Kozak-2004模型在0.6～0.9h处的MAPE 值高于其他两个模型；在其他相对高处，3 个模型的MAPE 值相差值不超过0.005，而且基本呈递增趋势，与许延丽[16]得到相似的结果；综合柱状图可得，Kozak-1988比Kozak-2004 和曾伟生模型在预测整个树干干形变化更加有优势。

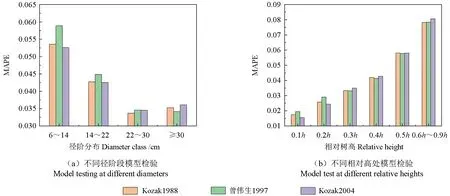
图5 3 种模型预测分析Fig.5 Model predictive analysis of the three models

基于上述结果可知，Kozak-1988（R2=0.978 3）的拟合结果最好，与总体检验结果一致，在模型预测分析中，也表现出较好的预测能力，因此Kozak-1988 为地基激光雷达提取落叶松人工林样地相对高处直径数据所建立的最优基础模型。

3.4 混合模型结果分析

基于上述研究，选取Kozak-1988 作为混合模型的基础模型，加入随机效应后，共3 种参数组合收敛而且显著相关（P＜0.05），4 个及以上参数组合均不收敛，拟合结果如表7所示，其中混合模型Kozak-1988（3）的AIC、BIC、LL 值最小，模型预估效果最好；混合模型检验统计量结果如表8所示，由表可知Kozak-1988（3）的RMSE 降低了0.046 6；Bias 降低了0.113，预估精度（p）提高了0.575%，基于树木效应的混合模型比基础模型拟合精度高，可为孟家岗林场落叶松人工林树干材积和蓄积量估算提供更精准估计。

表7 削度方程混合模型效应拟合结果比较Table 7 Fitting results of the mixed-effect model of trimming equation

表8 最优削度方程和最优混合验证统计量Table 8 Test of fit statistics for basic and mixed model

4 结论与讨论

4.1 结 论

本研究选取黑龙江省佳木斯市孟家岗林场的落叶松人工林为研究对象，以地基激光雷达获取的点云数据为基础，提取落叶松相对高处直径数据，结合皆伐后实测单木干形数据，对比其数据精度；通过TLS 数据构建落叶松削度方程；加入随机效应，建立基于样木效应的非线性混合模型，研究结果如下：

1）单木参数提取精度。TLS 提取的数据相关性较高（胸径R2=0.993 9，树高R2=0.913 9），胸径的提取效果好于树高；随着高度的增加，相对高处直径R2先增大，到相对高0.06h效果最好（R2=0.991 2），然后R2逐渐减小；由于树干上部点云数据质量下降，导致0.8h（R2= 0.876 3）和0.9h处直径相关性差于其他相对高处直径，但相对高处直径的R2基本都大于0.9，说明TLS 提取的数据质量满足精度要求，可以用于削度方程的构建。

2）基础模型。通过对9 个削度方程进行拟合与检验，Kozak-1988 的拟合结果最优（R2=0.978 3、RMSE=1.179 9）；为比较模型在不同径阶下和不同相对高处的预测精度，经过检验后对比分析发现，Kozak-1988 比Kozak-2004 和曾伟生模型更适合描述孟家岗林场落叶松的干形，因此Kozak-1988 为基于TLS 数据构建的最优基础模型。

3）混合模型。选取Kozak-1988 建立基于树木效应的混合模型时，b5、b6、b7作为混合参数时，各项拟合指标得到提高，即RMSE 降低了0.047；Bias 降低了0.113，预估精度（p）提高了0.575%，因此三参数的Kozak-1988 混合模型最优，可更好地预测树干干形的变化，估算树干材积，提供科学有效的经营措施。

4.2 讨 论

本研究使用202 棵皆伐样地单木干形数据对该研究进行补充，通过分径阶和不同相对高论证模型预测精度，更加充分考虑了落叶松树干干形的差异对模型的影响，有利于该研究的进一步推广和应用。与以往研究相比，通过随机参数的加入，使得构建的混合模型不同个数的参数进行组合，从而其检验指标相应得以改善。

激光雷达在林业中的应用表现出巨大的优势，其具有数据密度大、数据精度高、抗干扰能力强、作业效率高、不受太阳高度角和阴影的影响等优点，广泛应用于森林资源等三维动态监测，但是也存在一定的局限性，比如很难实现全三维信息的获取，以及激光雷达数据处理及提取算法目前还不够完善。地基获取的点云数据大、数据处理过程烦琐，虽降低了外业工作时间和成本，但内业数据处理耗时，如何提高林木参数自动化获取成为今后研究的热点。通过对树高、相对高0.8h及以上的直径精度进行分析发现，TLS点云数据的获取范围有限，不能完全反映上层树冠信息，如何通过合理的站点设置和确定TLS 获取点云数据样木的最高树高和最大样地面积仍需进一步实践；另外，花伟成等[6]使用MATLAB软件进行点云分割，将点云数据分为主干点云、分支点云和叶片点云，获得的主干点云效果较好，在一定程度上消除了分支和叶片点云对直径提取精度的影响；刑涛等[18]依据6 个特征训练xgboost 分类器，将蒙古栎人工林TLS 数据分为地面、树干与枝叶点云3 个类别，树干测试准确率达到了95%，两者将点云数据的分类处理对于后续研究提供了方向。除此之外，单木分割算法直接关系到数据的精度和应用，如何从算法方面提高单木分割准确率，减少错分、漏分等情况，是一直急需解决的问题。通过与无人机或者机载激光雷达点云数据进行融合，能很好地解决树高及上半部直径提取精度问题，由于没有ALS 数据，使得数据融合暂时不能进行，希望通过构建的削度方程能够较好地预测树干上部直径来解决此问题。对于TLS 获取的点云数据还包含其他信息参数，如高度变量、强度变量和密度变量等，如何把这些信息应用到削度方程构建，进而提高模型的预测精度，使得点云数据的利用率最大化，是后续研究应该重点关注的方向。

削度方程能较准确地反映完整树干的干形，利用落叶松人工林TLS 数据构建削度方程来寻找最优基础模型，然后根据最优基础模型构建基于树木效应的混合模型，实现对材积更高精度地预测[12]，为编制立木材积表和出材率表做准备，对精确估计落叶松人工林单木蓄积及合理指导造材具有重要作用。由于树干上半部点云缺失，用于构建削度方程的树干上半部直径数据相对较少，对树干上半部干形预测造成一定偏差；同时未考虑到点云获取的树干上部相对高数据对削度方程构建的影响，只是对总体的点云数据精度进行验证，没有对点云数据提取的相对高的最佳位置进行讨论[19]，后续研究对于削度方程模型构建和点云获取的相对高处直径数据的应用应该给予充分考虑。此外，冠长率、冠长、树冠高度[20]和形率[21]等影响树干干形变化，而且单木蓄积量和材种出材量还受到树皮厚度的影响[22-23]，而本研究在基础模型构建时没有考虑冠长率、冠长、树冠高度和形率等因素，它们将会对单株立木材积估算产生误差；随着后续研究工作的继续开展，以期寻找到综合考虑上述影响因素的最优削度方程，并且避免模型参数过多导致拟合不收敛的情况。