一种弹道修正弹SINS任意滚转角快速粗对准方法

王晗瑜,申 强,胡宝远,邓子龙,李 岩

(1. 北京理工大学机电学院,北京 100081；2. 北京理工大学重庆创新中心,重庆 401120；3. 西北工业集团有限公司设计二所,西安 710043)

0 引 言

二维弹道修正弹药是一类介于无控炮弹与制导炮弹之间的新型信息化弹药,通过弹载导航及弹道参数测量、简易修正模块提高打击精度,减少附带毁伤。其中,弹体姿态信息用于加速度计测量信号坐标转换、弹体姿态控制等,姿态估计精度直接影响弹道修正精度。

地磁传感器是目前国际上低成本修正弹药最主要的姿态测量手段,但精度偏低,测姿误差最大可达10°,无法满足弹体姿态控制要求,且极易受到强磁环境干扰,弹体飞行方向平行于地磁场方向时,存在奇异值。随着微机电惯性传感器成本降低、体积缩小、抗过载能力加强,其在智能弹药上的应用逐渐成为可能。基于多加速度计的无陀螺惯性测量方法标定及计算过程复杂,精度受安装结构影响较大,且无法满足弹道修正弹药成本低、传感器数量少的要求,工程实现可行性较低。结合弹体飞行动力学的微惯性姿态测量方法依赖于对系统模型和初始姿态的准确描述,计算成本高且不适用于滚转姿态完全未知的炮射弹药。基于卫星/微惯性传感器的组合测姿方法可实现低成本滚转姿态解算,但是卫星信号易受到电磁干扰,战时强对抗条件下可用性严重降低。无线电信标技术已用于一些武器的陆基导航,发展无线电信标/微惯性组合导航系统对于提高弹道修正弹药战场生存能力具有重要意义。Wright等验证了基于无线电信标测量位置速度的可行性,指出当弹体位于信标上方、信标布设分散且有几十米高程差情况下,可以达到与卫星导航系统同等的测量精度。然而实际战场环境中,对于射程一般在十几到几十公里的炮射弹药,信标仅可在炮位区域布设,布设个数、范围及地形有限,往往无法提供长时间、高精度、完整的三维测量信息,估计弹体姿态时可观性较差。

初始对准是惯性导航精确解算的前提,炮射弹药发射后弹丸滚转角处于随机状态。为解决捷联惯导大失准角空中初始化这一问题,孟东等、梅春波等建立了非线性卡尔曼滤波模型,Wang等、梅春波等建立了基于四元数的卡尔曼滤波模型。这些方法计算复杂,收敛速度慢,初始失准角过大时模型失效,无法满足炮射弹道修正弹药需要；同时,微惯导噪声源复杂,零偏特性受到高过载冲击后会发生改变,难以精确建模。神经网络具有很强的非线性函数逼近能力和容错能力,因此一些学者提出用神经网络模型替代卡尔曼滤波的初始对准方法,Rafatnia等建立了递归小波神经网络模型,实现了微惯性传感器非高斯白噪声和不确定偏差情况下的动基座对准,显著提高了对准精度。但是该方法需要在运动过程中实时训练,不适用于计算能力有限、飞行时间较短的弹道修正弹药。

考虑到弹道修正弹药发射后弹道特征已知,本文提出了利用弹道模型线下预训练神经网络,拟合初始滚转角与观测信息间非线性映射关系的方法,提高粗对准速度与精度。由于炮口处少量信标测量信息与姿态耦合关系较弱,失准角为弱可观状态,本文显性提取了捷联惯导自身测量参数作为输入神经元,提高了网络预测精度。

本文的结构安排为：首先建立初始滚转角与捷联惯导、无线电信标测量参数的函数模型,为建立神经网络模型奠定理论基础；然后采用主成分分析法优化网络模型,结合弹体飞行过程生成训练、测试数据；最后通过仿真模拟验证函数模型及提出的网络模型在对准速度、精度和适用失准角范围等方面的优越性,且具有很好的鲁棒性。

1 初始滚转角非线性函数模型

本文定义的相关坐标系如图1所示。

图1 弹体坐标系与发射坐标系Fig.1 Body coordinate system and launching coordinate system

(2)发射坐标系。原点是发射点在大地水准面上的投影,轴为弹道面和水平面的交线,射向为正,轴铅直向上,轴与轴、轴构成右手直角坐标系指向铅直面右方。为简化计算,本文取射击方位角为0°。考虑到弹道修正弹药射程近(小于50 km),飞行时间短,且微机电陀螺仪精度较低,因此将发射坐标系作为导航参考坐标系系,并忽略地球自转带来的影响。

考虑实际战场环境对无线电信标布设的简便性及快速性要求,在炮口左右两侧m各布设一信标。信标在发射坐标系下坐标分别为=(0,0,),=(0,0,-)。

1.1 初始滚转角与捷联惯导测量参数函数模型

根据捷联惯导反演算法,发射坐标系下的比力经过坐标转换后可以得到弹体坐标系下比力。

(1)

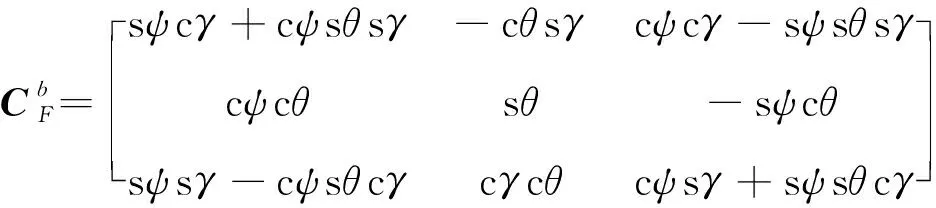
(2)

(3)

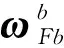
(4)

式(3)～(4)表示了陀螺仪测量角速度与滚转角之间的非线性函数模型,且仅轴、轴角速度与滚转角存在映射关系。

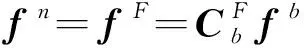
(5)

由式(1)可知是滚转角的函数,因此可得到导航系下比力与滚转角之间的函数模型。

1.2 初始滚转角与无线电信标测量信息函数模型

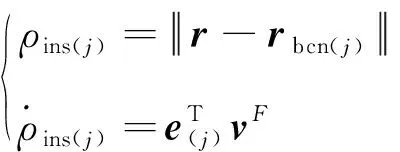
(6)

(7)

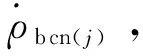
(8)

(9)

式中：δ为捷联惯导解算速度误差,δ为捷联惯导解算位置误差,()为的反对称阵,定义见文献[13]。

图2 5 s内捷联惯导解算积累的距离、距离率误差Fig.2 Accumulated range and rate errors of SINS within 5 s

卡尔曼滤波模型的状态量包括弹体在发射坐标系下的3维位置、速度和转速。即：

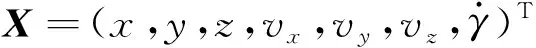
(10)

状态方程为刚体4D弹道方程,状态方程及状态转移矩阵()见文献[14]中相关结论。

观测量为信标接收机输出的距离和距离率：

(11)

观测方程为

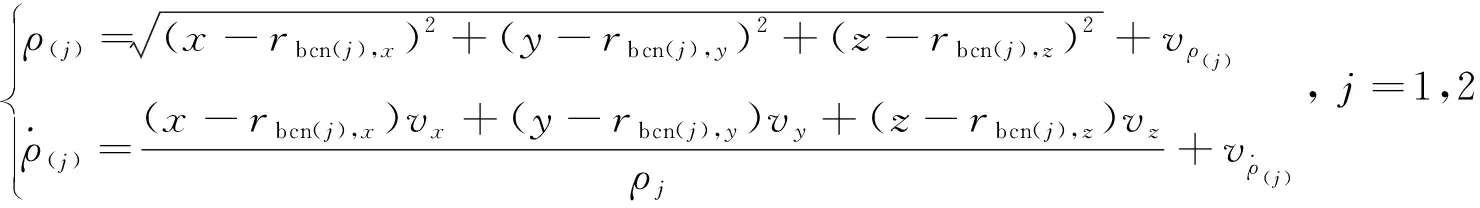
(12)

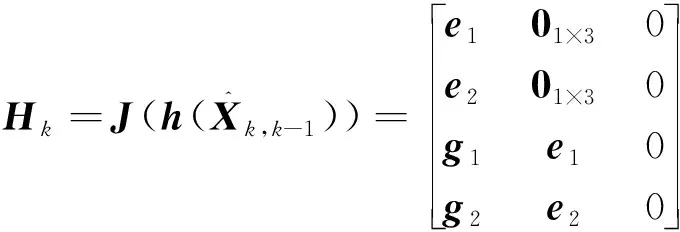
(13)

(14)

2 基于BP神经网络的弹道修正弹药粗对准模型

在第1节中建立了与初始滚转角有关的函数模型,传统对准方法在上述函数基础上建立非线性卡尔曼滤波模型,收敛速度慢,失准角较大时模型失效,不适用于炮射弹道修正弹药。根据Kolmogorov定理,三层神经网络在隐含层节点个数足够的情况下,就可对非线性函数进行无限逼近。因此,可利用神经网络这一特性逼近式(1)～(5)、式(8),对弹体滚转角进行快速估计。

2.1 BP神经网络输入输出参数选取策略

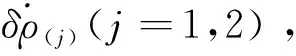
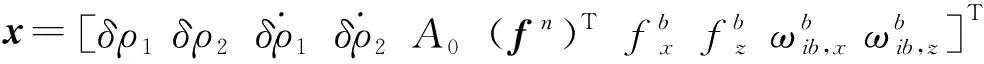
(15)

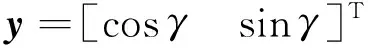
(16)

2.2 BP神经网络特征提取

式(15)选择的输入特征之间具有较强的相关性,导致网络模型结构复杂,训练时容易陷入局部最小值点,模型泛化能力变差。因此,本文采用了主成分分析(Principal components analysis,PCA)的方法进行特征提取,将原始输入变量线性变换为一组不相关的主成分,同时尽可能保留原始变量中的主要信息。该算法详细步骤如下：

对于维输入变量,每维变量有个样本,即：

(17)

1) 数据标准化。

2) 计算相关系数矩阵。

3) 计算相关系数矩阵的特征值(=1,2,…,)及相应的特征向量,并按照特征值降序排列。

4) 根据式(18)～(19)计算各特征值的贡献率(=1,2,…,)和累积贡献率(=1,2,…,),选择累积贡献率达到95%以上的特征值作为主成分。

(18)

(19)

2.3 BP神经网络训练、测试数据模拟

生成测试数据时,不仅考虑了实测惯性传感器静态噪声及信标接收机模拟噪声,并且为验证模型泛化能力,设置了射角、俯仰角对准误差不在训练范围内以及信标位置存在误差的测试环境,参数设置见表1。其中,射角间隔在测试环境A中设置为1°,其他测试环境中设置为2°,俯仰角对准误差间隔均为1°。

表1 测试数据参数设置Table 1 Test data parameters set

3 仿真校验及模型评估

3.1 神经网络非线性函数模型验证

初始滚转角与惯导自身参数函数关系验证

以某型榴弹弹体飞行轨迹为例,射角35°,初始合速度930 m/s时,飞行总时间为96 s,总射程为29.34 km。令=5 s,=10 s,图3验证了由式(1)～(9)表示的非线性函数(以轴为例),并引入了传感器实测噪声。其中加速度计零偏均值分别为1.15×10,2.8×10,9.2×10,陀螺仪零偏均值分别为27.86(°)/h,49.97(°)/h和2.58(°)/h。

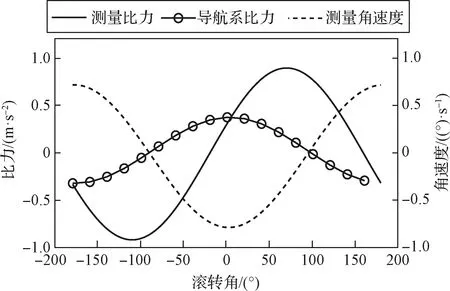
图3 初始滚转角与x轴比力、角速度关系Fig.3 Relations between the initial roll angle and x-axis specific force and angle rate

初始滚转角与测距测速误差函数关系验证

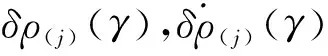
图4 滤波后左侧信标测量距离、距离率精度随滚转角变化Fig.4 Curves of the filtered range error and range rate error measured by the left beacon with the roll angle

3.2 基于神经网络的粗对准模型评估

神经网络采用单隐藏层结构,隐藏层神经元个数为5,由带动量因子的和具有自适应学习速率梯度下降的traingdx函数训练,最大训练轮数设置为5000。根据式(18)～(19),前6维主成分累计可信度可达99.89%。因此,本文建立的PCA-BP神经网络输入神经元为6维。

用于模型评价的精密度指标为预测结果的均方根误差(RMSE),准确度指标包括平均绝对误差(MAE)与最大绝对误差(Max-AE)。

多输入神经网络模型精度评估

表2 模型一、二预测结果Table 2 Prediction results of Model 1 and Model 2

可以看出,在测试环境A下,模型一的预测精密度及准确度远远优于模型二。这说明,仅依赖于炮口信标提供的距离、距离率信息的模型可观测度很差,增加捷联惯导测量信息作为输入层神经元可以显著提高网络的预测精度。

模型快速性及适用失准角范围评估

炮射弹道修正弹飞行时间较短,且发射后滚转角处于随机状态,模型必须实现任意初始状态下快速对准。本模型中,无线电信标测速精度是制约粗对准时间的主要影响因素,即只有当滤波之后的测量噪声小于(-)时间内积累的距离率误差时,该对准模型才是有效的。

为有效评估本模型的快速性,分别模拟了无线电信标测速误差为0.1 m/s,0.5 m/s和1 m/s时所需的对准时间。经过卡尔曼滤波之后,无线电信标测速误差分别为0.034 m/s,0.163 m/s和0.341 m/s。不同对准时间下,距离率误差随滚转角变化的平均绝对值见表3,因此,当无线电信标测速误差为0.1 m/s时,需满足对准时间≥10 s；测速误差为0.5 m/s时,需满足≥17 s；测速误差为1 m/s时,需满足≥20 s。

表3 不同时刻下平均绝对距离率误差Table 3 Average absolute range rate errors at different times

以射角35°为例,在A组测试环境下,模拟了不同测速精度的信标辅助下,对准精度随对准时间变化,见表4。可以看出,对准时间越长,对准精度越高,但受到网络模型限制,超过一定时间,对准精度提高不再明显,因此实际应用时,取网络模型最短对准时间进行粗对准,再切换到精对准,可提高对准效率。

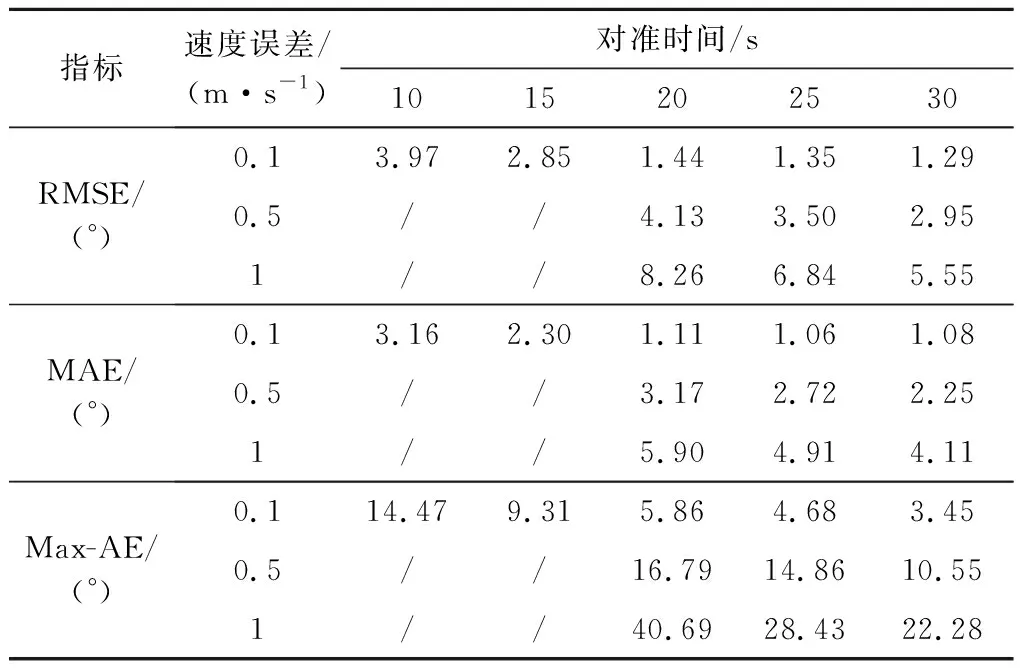
表4 对准结果与信标测速误差、对准时间的关系Table 4 Relations between the alignment results and the beacon-measured range rate errors and alignment time

少量信标辅助下,线性卡尔曼滤波可快速收敛的最大初始误差范围在20°～30°,因此假定30 s内滚转角误差可收敛到25°内时,该粗对准模型有效。为进一步验证本文提出的粗对准模型快速性及失准角适用范围广泛性,以射角35°为例,在A组测试环境下,对比了基于扩展卡尔曼滤波(Extended Kalman filter, EKF)的非线性卡尔曼对准模型和基于加性四元数误差(Additive quaternion error, AQE)的线性卡尔曼对准模型,可有效收敛的初始失准角范围和该范围内最大失准角下完成粗对准所需时间见表5。不同初始误差下的对准结果如图5所示,其中PCA-BPNN模型以信标测速误差为1 m/s为例。可以看出,本文提出的基于神经网络的粗对准模型可在任意失准角范围内快速完成粗对准,其适用角度广泛性和快速性明显优于传统的卡尔曼滤波方法。

表5 不同模型适用失准角范围和对准时间对比Table 5 Comparison of applicable misalignment angle ranges and alignment time of different models

图5 不同模型粗对准结果对比Fig.5 Comparison of the coarse alignment results of different models

模型鲁棒性评估

为评估本文提出的粗对准模型在实际作战使用时的鲁棒性,以信标测速误差0.1 m/s为例,在射角未在训练范围内的场景B、射角与初始俯仰角误差均不在训练范围内的场景C及考虑信标布设位置误差的场景D下进行测试,并与未进行优化的BPNN进行对比,结果见表6。其中同一测试环境下精度较高的结果用粗体表示。

从表6可以看出,三种测试场景下,PCA-BPNN的均方根误差和平均绝对误差在8°以内,最大绝对误差在25°以内,且能在发射后10 s前完成,满足弹道修正弹粗对准精度要求。

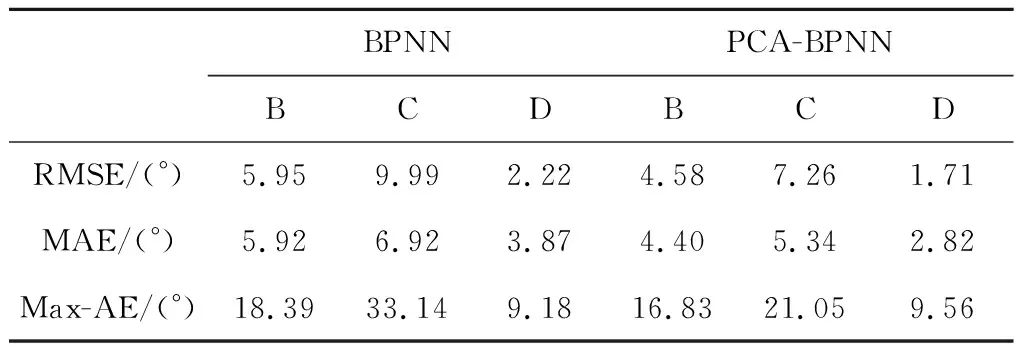
表6 不同测试环境下BPNN和PCA-BPNN预测结果Table 6 Prediction results of BPNN and PCA-BPNN in various testing environments

同信标布设位置误差相比,未在训练范围内的射角和初始俯仰角误差对最大绝对误差值影响较大。因此使用时尽量对所有可能的射角范围和初始俯仰角误差范围进行训练,以获得更高的对准精度；本方法对信标布设精度没有很高的要求,实际应用具有较高的简便性。

同BPNN相比,本文提出的PCA-BPNN模型在B, C, D多种测试环境下预测精密度和准确度均明显优于BPNN。建立的PCA-BPNN不仅由较少的输入变量组成,具有简单的网络结构,在弹载计算机上离线应用时计算量小；并且由于输入数据降维有利于神经网络参数的优化迭代,提高了网络模型的预测精度和泛化能力。

综上所述,与基于非线性卡尔曼滤波进行大失准角粗对准的经典方法不同,本文提出的方法结合弹道模型线下训练BP神经网络,在应用时仅需将训练好的网络保存到弹载计算机中,计算简单,便于实现,对准速度快,在-180°～180°的失准角范围内都具有较高精度。

4 结 论

针对炮射弹药发射后滚转角完全未知且信标测量值可观性较差的难点,本文提出了结合弹道模型建立优化后的神经网络模型进行线下训练,并加入捷联惯导参数作为输入神经元的快速粗对准方法。仿真结果表明,无论失准角大小,本文提出的粗对准方法均可在发射后10 s内快速完成对准,相比于传统基于卡尔曼滤波的对准方法,快速性、对准范围及鲁棒性均明显提高,为炮射弹道修正弹药出炮口后任意滚转角条件下的快速粗对准提供了参考。