月面着陆动力下降段最优轨迹序列凸优化方法

邓雁鹏,穆荣军,彭 娜,吴 鹏

(1. 哈尔滨工业大学航天学院,哈尔滨 150001；2. 上海航天电子技术研究所,上海 201109)

0 引 言

为顺利实施月球着陆探测器自主避障、保证精确安全着陆,通常将月球着陆过程细分为4个阶段,如图1所示。月球着陆器在动力下降段之前处于远地点100 km、近地点15 km的转移轨道上。自近地点附近开始动力下降,然后开始进行姿态调整,经过10～20 s的姿态调整后开始避障。动力下降段的主要目标为尽可能降低着陆器的高度和速度,通常历时约500 s,航程500 km左右；着陆器高度从15 km降低到3 km,速度将从1.7 km/s降低到0左右。该阶段通常会消耗掉着陆器约80%的燃料,因此该段制导算法要求,在着陆器具有初始状态误差和模型不确定性的情况下尽量减少燃料消耗并在终端达到后续姿态调整、避障着陆的入口状态要求。由于着陆器在经过环月轨道离轨后存在霍曼转移轨道偏差和点火时间偏差,进而造成初始位置偏差。因此,本文充分考虑初始位置偏差的影响,提出了一种基于最优轨迹序列凸优化的在线制导方法,在节省燃料的基础上实现高精度动力下降制导。

图1 典型月面着陆过程Fig.1 Typical lunar landing process

月面着陆制导算法主要分为三种类型：重力转弯制导、显式制导和标称轨迹制导。其中重力转弯制导算法原理简单,但其不具备燃料经济性,同时对末端着陆位置没有约束,故无法实现精确着陆。

显式制导算法能够对着陆位置实现精确控制,同时由于其具有自主性,实时性与燃料消耗次优性,因此近些年得到了广泛的研究与应用。文献[1]依据动力学模型将月面软着陆下降制导分为纵向平面运动和横向运动并分别设计制导律,其纵向平面运动采用改进显式制导算法,横向运动采用ZEM/ZEV制导律并对脉宽脉频进行脉冲调制。文献[2]针对动力下降段的制导问题,在显式制导算法的基础上,提出了自适应动力显式制导方法。通过对动力下降段目标的自适应调整使其满足接近段入口条件,通过在线实时估计推重比与比冲等参数实现制导参数的自适应调整,由此实现月面高精度高可靠性着陆。

显式制导虽算法简洁、应用广泛,但通常未考虑月面着陆制导过程中所关注的燃料最优性问题。相对显式制导算法而言,基于最优化原理的数值优化算法按照一定的目标及约束条件设计标称轨道。在飞行过程中或根据偏差进行实时最优轨迹规划,或通过实时比较着陆器的位置和速度测量信息,导引着陆器飞向着陆目标点。该方法通常消耗更少的燃料,具有更强的鲁棒性。但其通常具有计算量较大,实时性难以保证等缺点。

传统轨迹优化方法分为直接法和间接法。间接法利用极小值原理,通过引入拉格朗日乘子法进行求解。但其初值难以获得,该解法对于初值又比较敏感,限制了该方法的应用。直接法是将着陆轨迹优化问题转化为多种路径约束和边界约束下的静态参数优化问题,进而采用数值优化方法求解。数值优化算法主要分为二次规划算法和凸优化两类。第一类是将原问题通过伪谱法进行离散化,将其转化为非线性规划问题,利用非线性规划方法进行求解。例如文献[4]利用高斯伪谱法实现了着陆器在二维情况下的软着陆轨道规划；在此基础上文献[5]利用高斯伪谱法+序列二次规划算法设计最优着陆轨迹。文献[6]提出了一种具有路标点约束的多阶段非线性优化制导方法。这一算法在最大程度减少燃料消耗的同时,可确保着陆器在着陆过程中通过两个规划的路标点,使视觉探测器能够在通过这些路标点时进行着陆点检测,进一步确保任务的安全性。

伪谱法+序列二次规划算法随着问题规模增大,计算量将显著增长,规划效率难以满足实时应用需求。相比于伪谱法+序列二次规划算法,基于凸优化的轨迹规划算法通常具有更小的计算量,同时凸问题能够保证局部最优解即为全局最优解。因此,第二类算法将非线性轨迹规划问题转换为凸问题后,再进行离散化,进而对该问题进行求解。例如文献[8]针对小型天体弱引力场所导致的动力学非线性问题,在凸优化过程中采用局部线性化的方式对原问题进行凸化处理。除采用局部线性化外,在着陆轨迹规划中,还常采用变量松弛的方式将原非凸问题转化为凸问题求解。文献[9-10]分别针对月面与行星着陆问题,通过松弛变量将原非凸问题转化为二阶锥规划(Second-order cone programming, SOCP)问题,引入内点法求解,并通过数值模拟证明了所提出方法的性能。针对非线性气动阻力不可忽略的可重复使用运载器着陆过程中的燃料优化问题,文献[11]提出了一种快速弹道优化方法。该算法通过同伦迭代策略来凸化火箭的非线性系统动力学,通过逐次迭代逐步逼近时变阻力剖面。该算法不需要参考轨迹或初始猜测,极大地增强了算法的自主性。除采用松弛算法对原问题进行无损凸化外,文献[12]针对火箭高空再入定点回收问题,提出了一种考虑气动力和推力控制的多约束轨迹优化方法,使用无损凸化对升力约束和推力约束进行松弛,最终将问题转化为SOCP问题进行序列迭代求解。但其将重力加速度建模为常矢量,且未考虑惯性加速度项的影响。基于此,针对月面着陆动力下降段最优轨迹优化问题,有必要建立强非线性时变项影响下的精细化动力学模型并对该方法做出对应调整,实现动力下降段最优轨迹的在线快速迭代求解。

以上文献对于时变加速度剖面通常采用两种处理方式。部分文献采用在月心惯性坐标系下建模的方式消除动力学模型中的惯性力项,如文献[1,13]。在此坐标系下的着陆动力学模型较为简单,但其三个方向上的坐标不能直接反映着陆器高度、航程等信息,也难以添加相应的姿态约束以满足导航与避障传感器的需求。同时,如图2所示,着陆器飞行过程中重力加速度的大小虽基本不变,但由于月球曲率的存在,其方向在不断改变；如不对这一部分的时变加速度进行精细化建模,将会影响最终制导精度及燃料消耗。此外,部分文献选择在月面固连坐标系下建模,将该坐标系下的重力加速度作为定常矢量处理,同时忽略在此坐标系下难以建模和补偿的惯性加速度项的影响。在此坐标系下的动力学模型中,着陆器三轴坐标分别代表了高度与水平两个方向的航程,三轴姿态角可直观反映着陆器相对于月面的姿态,具体物理意义明确,从而易于根据导航与避障传感器需求添加相应的姿态约束。但由于建模时通常将重力加速度考虑为常矢量,同时月面曲率与自转引起的惯性力项的非线性特性难以求解,一般仅能应用于惯性力较小可忽略、位置变动较小的末制导阶段。

图2 着陆器动力学模型Fig.2 Dynamics model of the lunar lander

同时,经典凸优化算法对于非线性项一般通过序列凸优化算法进行处理,即通过一系列凸近似手段将原复杂非凸问题转化为凸问题,从而快速获得原优化问题的近似最优解。尽管该方法计算效率较高、实用性较强,但仍需要依赖初始参考轨迹,利用Taylor展开使模型实现线性化,将其转化为凸问题后开始迭代求解。与此同时,该算法需要对该问题施加额外的信赖域约束,以保证线性化的有效性。此外,该算法的收敛性与参考轨迹的质量具有一定的相关性,这类似于非线性规划中的初值敏感性问题,目前很少有文献针对这一内容有所讨论。序列凸优化依赖于初始参考轨迹的特性弱化了局部最优即为全局最优这一凸优化的主要优点。因此,为提高算法的求解精度及自主性,本文提出改进序列凸优化算法,将时变加速度剖面同伦地添加到原非线性模型中序列迭代求解,使得该算法不依赖初始参考轨迹,增强了算法的自主性和多种应用场景适应能力。

本文结合凸优化计算量小、实时性高的优点,提出了一种基于序列凸优化的月球探测器动力下降段在线制导方法。综合考虑月球探测器动力下降段在线轨迹规划的快速性、制导精度与燃料消耗等需求,针对月球着陆过程中引力加速度与惯性加速度时变特性及模型复杂、难以求解等问题,首先在月面固联坐标系下建立了考虑月面曲率和月球自转的精细化着陆动力学模型,在此基础上提出考虑时变加速度剖面的序列凸优化算法。区别于经典序列凸优化算法通过对动力学模型的序列线性化将原问题转化为凸问题并进行求解,本文以燃料消耗为性能指标,综合考虑推力大小等约束条件,针对月面着陆飞行过程中,惯性加速度剖面逐渐趋于0,重力加速度逐渐趋于定常的特点。在提出迭代算法的基础上,首先求取考虑重力加速度为常数,惯性加速度为0时原问题的解。然后保持问题为凸问题,将时变加速度同伦地添加到该问题中进行序列迭代求解。由于该方法在不需要求解Jacobi矩阵,减少了计算量；同时非线性项的凸化不是基于线性化,因此不需要参考轨迹或初始猜测,增强了算法的自主性,有利于在线应用。最终,通过与凸优化、多项式制导算法进行仿真对比,并针对多种初始偏差开展打靶分析,验证了算法性能。

1 精细化月球着陆动力学模型

1.1 月球着陆器动力下降段动力学模型

本文考虑到在月面固连参考坐标系下三个坐标轴方向上的坐标可直接反映着陆器高度航程等信息,也易于添加相应的姿态约束以满足导航与避障传感器的需求的优点。在月面固连参考系下建立精细化月球着陆动力学模型,并通过序列凸优化算法实时的估计时变加速度剖面。此时,着陆器的动力学模型为：

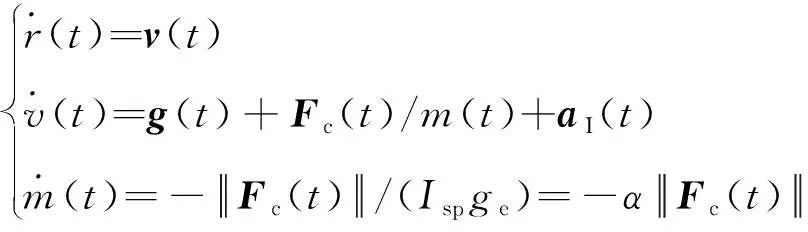
(1)

式中：(),()分别为着陆器的位置和速度；()为着陆器推力；()为着陆器质量；为推力器比冲；为标称地球重力加速度；(),()分别为惯性加速度与重力加速度,它们均随时间变化。因此,采用考虑时变加速度剖面的着陆器动力学模型,通过序列凸优化算法实现对(),()的估计与补偿,进而保证算法的最优性。

由式(1),有

(2)

两边积分可得着陆器剩余质量：

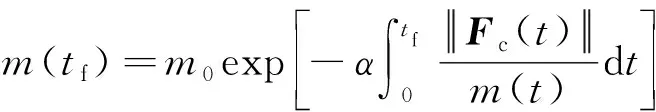
(3)

为使得最终质量()达到最大,需要以下目标函数达到最小,

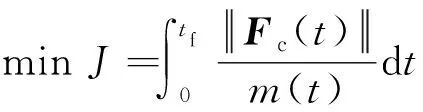
(4)

在着陆过程中,为避免着陆器撞击到月面,需要引入与着陆安全性相关的约束。首先引入高度约束：

()≥

(5)

式中：为着陆器被允许到达的最低高度,低于此高度则有撞击月面的风险。

基于安全考虑,在末制导阶段通常还需要引入视线角约束。令

()=()-

(6)

则要求

(7)

式(7)要求着陆器在着陆轨迹上任意位置处相对于目标点的连线与水平面的夹角要大于。由于本文主要针对着陆器动力下降段应用场景,该段末了点的高度足够高,通常远高于着陆场地形起伏的程度；同时考虑到着陆器在动力下降段航程较长,相对航程而言下降高度较小,视线角无法起到约束效果。因此,在动力下降段可忽略式(7),此时并不会影响着陆安全性。

除着陆安全性带来的约束之外,还需考虑推力约束与剩余质量约束,其中推力约束如下：

(8)

式中：,为推力器能提供的最小与最大推力。

剩余质量约束如下：

()≥

(9)

最后还有着陆器初末状态约束：

(10)

以上动力学模型和约束共同构成了如下非凸优化问题：

(11)

1.2 无损凸化

在式(1)表示的动力学模型中,由于()出现在分母上,因此优化问题式(11)为非凸模型。为使用凸优化方法求解,需要将模型进行凸化,转化为一个凸问题,具体而言为一个SOCP问题。参考文献[16]凸化方法,首先引入对数质量

()=ln()

(12)

同时引入新的控制变量

(13)

在此基础上,动力学模型变为

(14)

目标函数变为：

(15)

推力幅值约束为

e-()≤()≤e-()

(16)

剩余质量约束变为：

()≥

(17)

还需引入控制量约束

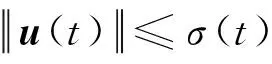
(18)

当取得最优解时有

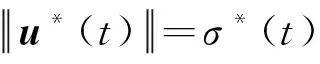
(19)

为了避免指数形非凸约束,将式(16)进行Taylor展开有

(20)

式中:()满足

()=ln(-)

(21)

式中：为着陆器初始质量。

对数质量()还需要满足以下约束

ln(-)≤()≤ln(-)

(22)

故原问题化为以下SOCP问题

(23)

2 问题的离散化

对式(23),还需进行离散化再进行求解。定义状态变量如下

(24)

动力学模型式(14)变为

(25)

式中：

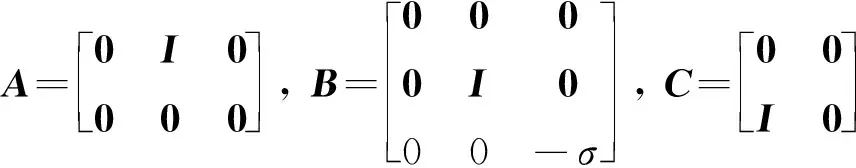
离散化的方法为：将时间区间[0,]离散化为个区间,在每个区间内,假设第个时间区间内的控制量为()满足

(26)

式中:(·)为特定的基函数。在本文中,取基函数(·)为常数函数。离散化的动力学模型为

+1=++(+I)

(27)

式中：,,,即为(),(),(),I()。

=Δ+,=Δ,=Δ

式中:Δ为离散化的时间步长Δ=。

离散化后,问题变为

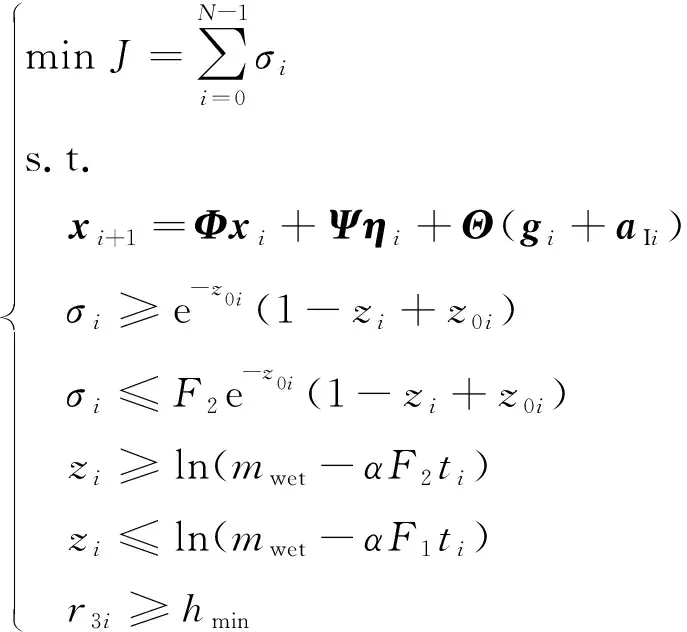
(28)

式中：=(),=(),=(),0=(),3=()。式(28)中的第一式为着陆性能指标,描述为各节点加速度幅值的和；第二式为动力学约束；第三、四式为推力大小约束；第五、六式为质量约束；第七式为高度约束。

3 考虑时变加速度剖面的制导模型

惯性加速度的来源为离心力与科里奥利力,其满足：

(29)

式中：()为着陆器与月球的相对速度;()为着陆器相对于月球的角速度;为月球的自转角速度;为的叉乘矩阵形式：

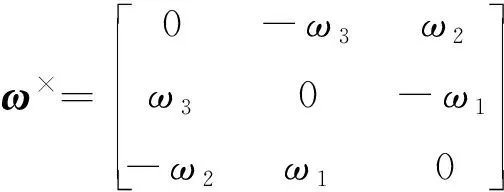
在本问题中,前两个量(),()均为时变量,因此惯性加速度()也为时变量。

除惯性加速度()之外,月球引力加速度在月面固连坐标系下也有微小的变化。如考虑月球引力模型到项,则引力加速度随着着陆器纬度与高度的变化会有微小的变化。在本文中,取月球引力常数=4.902801056×10m/s,归一化项引力摄动系数为=-9.08×10。

根据上述模型,对时变加速度剖面也采用离散化处理,具体计算过程如图3所示。在每一个离散点处,均采用上一制导周期的计算结果作为标称的()与()初值,计算时变加速度剖面,并将该加速度剖面用于本制导周期凸优化中；在进行一次凸优化之后,将本次凸优化结果中的(),()与此前(),()进行比较。如果二者差值在一定范围内,则认为收敛,输出凸优化结果；否则根据此次结果重新计算时变加速度剖面(),()并再次进行凸优化。如此反复进行序列凸优化,直至收敛,完成本次迭代周期的计算。

图3 基于序列凸优化的在线制导算法流程图Fig.3 Flow chart of the online guidance algorithm based on sequence convex optimization method

4 仿真校验

以嫦娥系列着陆器典型参数为例,假设着陆器初始质量为3000 kg,发动机最大推力为7500 N,最小推力900 N,真空比冲309 s；初始速度=1700 m/s,==0,末速度=50 m/s,=0,=-50 m/s；初始高度15 km,最终高度3 km。本文将所提出的序列凸优化算法与常规凸优化、多项式制导相比,以表明其在燃料消耗等方面的优势；同时将本文方法与LGR伪谱法进行对比,以明确其在计算效率上的优越性。本文数值仿真计算机采用Intel Core i7-10700U 2.90 GHz CPU,CVX工具箱和GPOPS-II求解器进行解算。

4.1 仿真结果

各方法制导结果由表1与图4～图9所示。由序列凸优化方法,LGR伪谱法,凸优化方法与多项式制导均实现了制导目标。参照图4～图9,LGR伪谱法与序列凸优化算法计算结果一致、同样取得了最优解。序列凸优化,其中序列凸优化与多项式制导方法用时578 s,凸优化用时643 s,节约65 s。这是由于凸优化模型未考虑离心惯性力的影响,因而离心惯性力在着陆器飞行过程中作为干扰项存在,在每个制导周期重新规划最优着陆曲线时,为使凸优化问题有界,对着陆时间调整导致的,由于用时较短,序列凸优化方法与多项式制导方法的燃料消耗也显著小于凸优化方法。

表1 各制导方法结果对比Table 1 Comparison of results of each guidance method

图4 质量变化曲线Fig.4 Mass variation

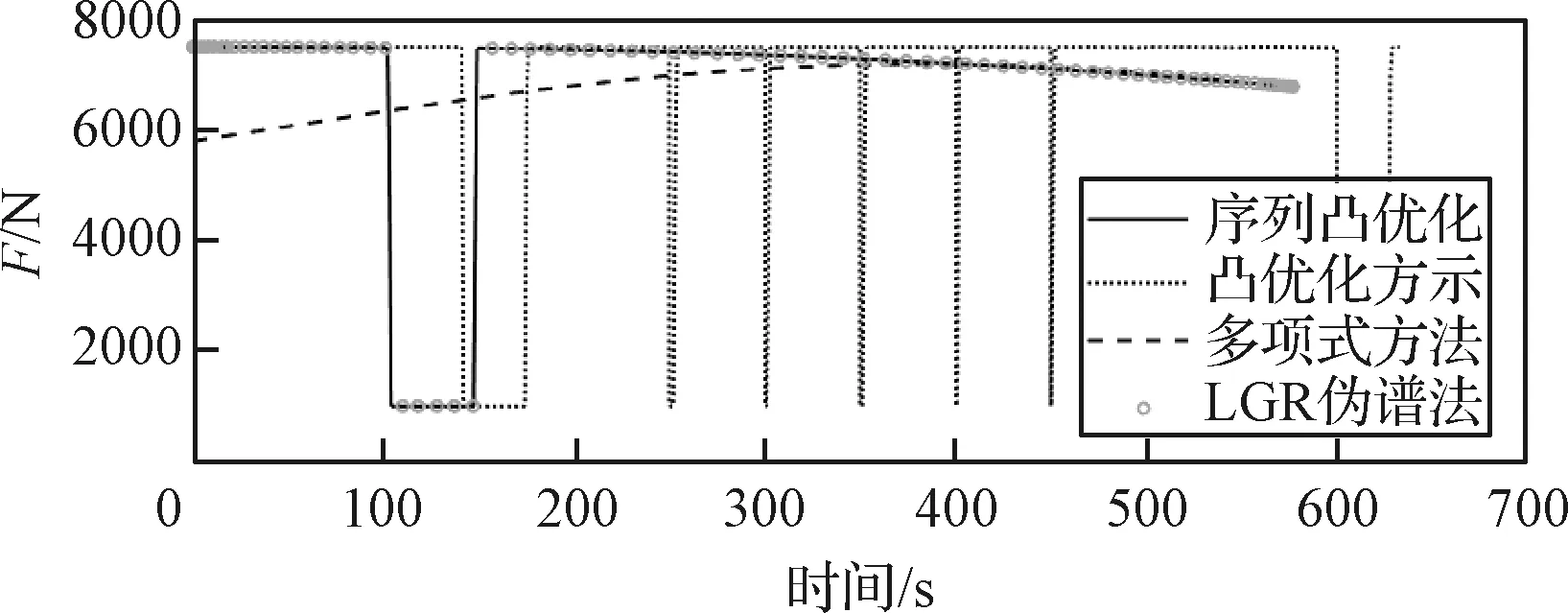
图5 推力变化曲线Fig.5 Thrust variation

图6 软着陆过程速度曲线Fig.6 Velocity during soft landing

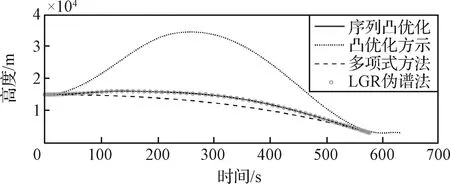
图7 软着陆过程高度曲线Fig.7 Altitude during soft landing

图8 软着陆过程航程曲线Fig.8 Flying range during soft landing

图9 软着陆过程俯仰角曲线Fig.9 Pitch angle during soft landing

如图4所示,采用序列凸优化算法最终剩余质量1666.4 kg,采用多项式制导方法最终剩余质量1664.2 kg,序列凸优化方法节约燃料2.2 kg。

如图5所示,采用序列凸优化算法构造的制导指令推力值近似符合传统变分法推导的max-min模式,推力值近似在最大与最小之间切换,切换次数为2。而采用凸优化方法则完全符合max-min模式,但由于每一个制导周期重新规划的制导指令与上一周期的制导指令有较大偏差,造成推力指令在最大与最小之间反复切换,这对执行机构执行该制导指令带来一定困难；对于多项式制导方法,推力值为一条平滑曲线,其后段与序列凸优化方法几乎重合,这由于在动力下降段末期,时变的惯性加速度带来的影响几乎可以忽略,而多项式方法在此时也具有最优性,因此二者重合。

三轴速度如图6所示。四种算法在东向速度曲线和北向速度曲线上表现相似,而在天向速度方面,凸优化算法与其余算法相差较大,这是因为凸优化算法没有考虑离心加速度的影响；同时序列凸优化算法形成的速度剖面具有分段光滑特性,这是由于max-min的控制模式导致的。图7为高度曲线,由图可以看出采用凸优化方法的飞行高度显著大于其余方法,这是由于凸优化算法未考虑离心加速度导致的；而序列凸优化算法的飞行高度仅略高于多项式算法。图8为着陆器航程曲线,可以看到在本文所示的典型参数下,四种方法航程一致,均为557 km,结合图7可以看出着陆器典型下降高度为12 km,对应中的为1.2°,如此小的起不到约束效果。因此,本算例进一步说明了在动力下降段,可以忽略约束式(7),此时并不会影响着陆安全性。

俯仰角曲线如图9所示,由图可知,凸优化算法的俯仰角在制导各个周期反复的大幅度切换,这对控制系统实现带来了一定的问题；而对于序列凸优化方法,在飞行过程中俯仰角仅有两次幅度较小的突变,控制系统较容易实现；而多项式方法则在全程呈连续变化。

4.2 求解效率分析

按第4节仿真初始条件,对改进序列凸优化算法和LGR伪谱法的求解效率进行对比验证。

由图4～图9及表1可看出序列凸优化算法与LGR伪谱法所得结果一致,均达到了最优解,实现了燃料消耗最优。下面就序列凸优化算法的收敛性及计算效率进行分析,并与LGR伪谱法进行比较。

图10为每次序列迭代求解消耗时间。由图可知,平均消耗时间为0.2343 s,其中耗时最长的一次计算耗时0.2678 s,出现在第二步,这是由时变加速度剖面在第二步被突然地加入其中所致。

图10 序列计算耗时Fig.10 Time consumption of sequential calculation

图11为各次序列计算所得高度曲线。可以看出,前两次计算曲线相差较大,而后曲线很快地收敛,第3次与第8次所得曲线已几乎重合。为进一步衡量算法的收敛性,以得到收敛速度,计算前后两次计算所得高度剖面()的差,将其平均值作为衡量指标,即：

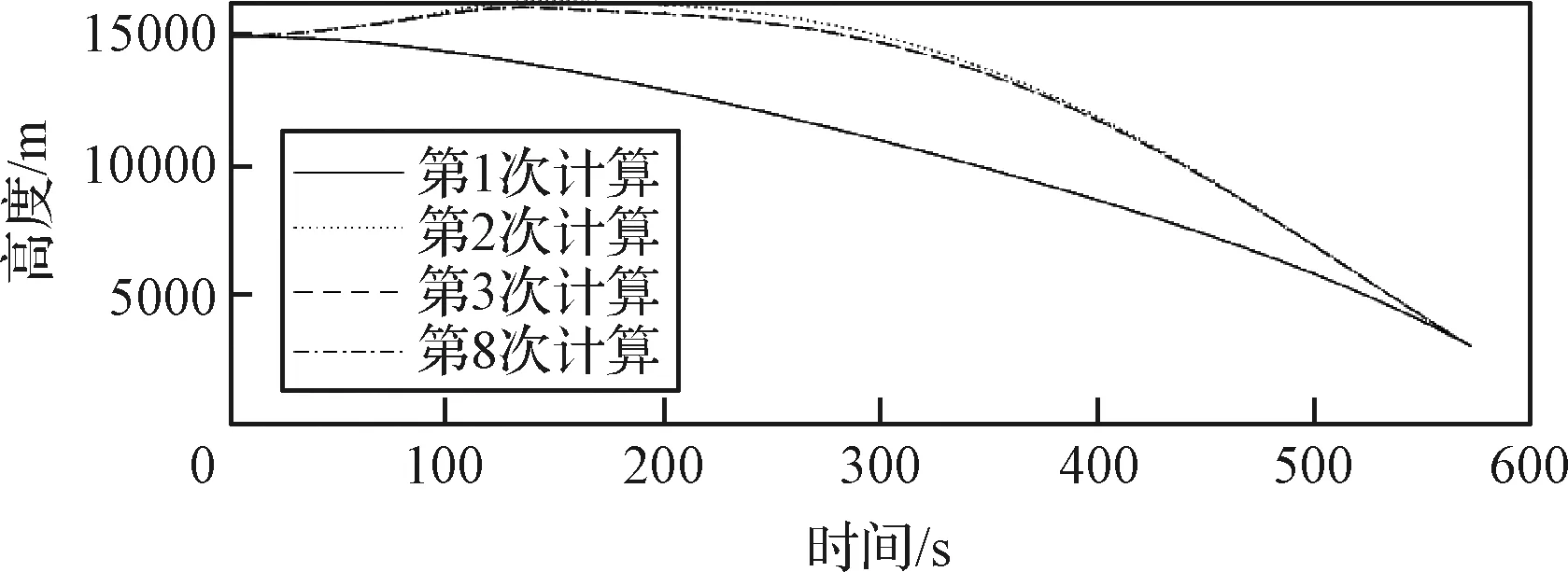
图11 每次计算所得高度曲线Fig.11 Curves of calculated altitude

(30)

式中:3,()为第次序列计算所得着陆器高度剖面;为着陆器飞行时间。类似地,还可以定义：

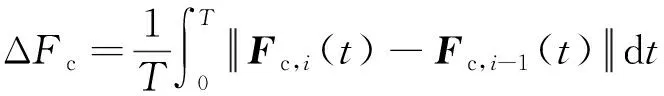
(31)

式中:c,()为第次序列计算所得着陆器推力指令。若式(30)与(31)趋于0,则说明轨迹及推力指令不再随序列凸优化发生变化,算法收敛。图12与图13分别为高度剖面以及推力指令的收敛过程,由于Δ与Δ变化范围较大,纵轴采用对数坐标。由图可以看出,前9次序列计算轨迹和指令均迅速收敛。其中Δ由111.3 m收敛到6.9×10m, Δ由2151 N收敛到8.2×10N,而后在这附近小范围波动。最大波动范围Δ<3.3×10m, Δ< 2.5×10N。就导航系统精度及推力系统精度而言,轨迹规划只需要收敛至1.0×10m以内,推力指令收敛到0.1 N以内即可。由图可知,计算至第6次即可满足精度要求,此时序列凸优化算法总用时1.446 s,而伪谱法用时27.45 s,计算效率提高94.73%。以上为对初始轨迹规划所用时间的分析。此外,除在初始轨迹规划外的每个制导周期重新进行轨迹规划时,可利用上一制导周期的结果作为序列计算初始值,此时仅需要计算1至2次即可符合收敛性要求。对历次制导周期的收敛次数以及收敛时间进行统计,可知约78.3%的制导周期仅需要计算一次,21.7%仅需要计算两次即可满足收敛性要求,平均耗时0.2851 s,最长耗时0.5801 s。

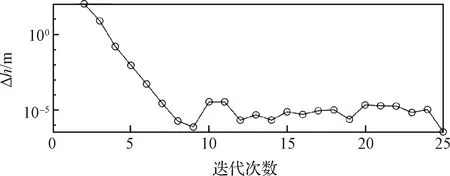
图12 高度剖面收敛过程Fig.12 Altitude profile convergence process

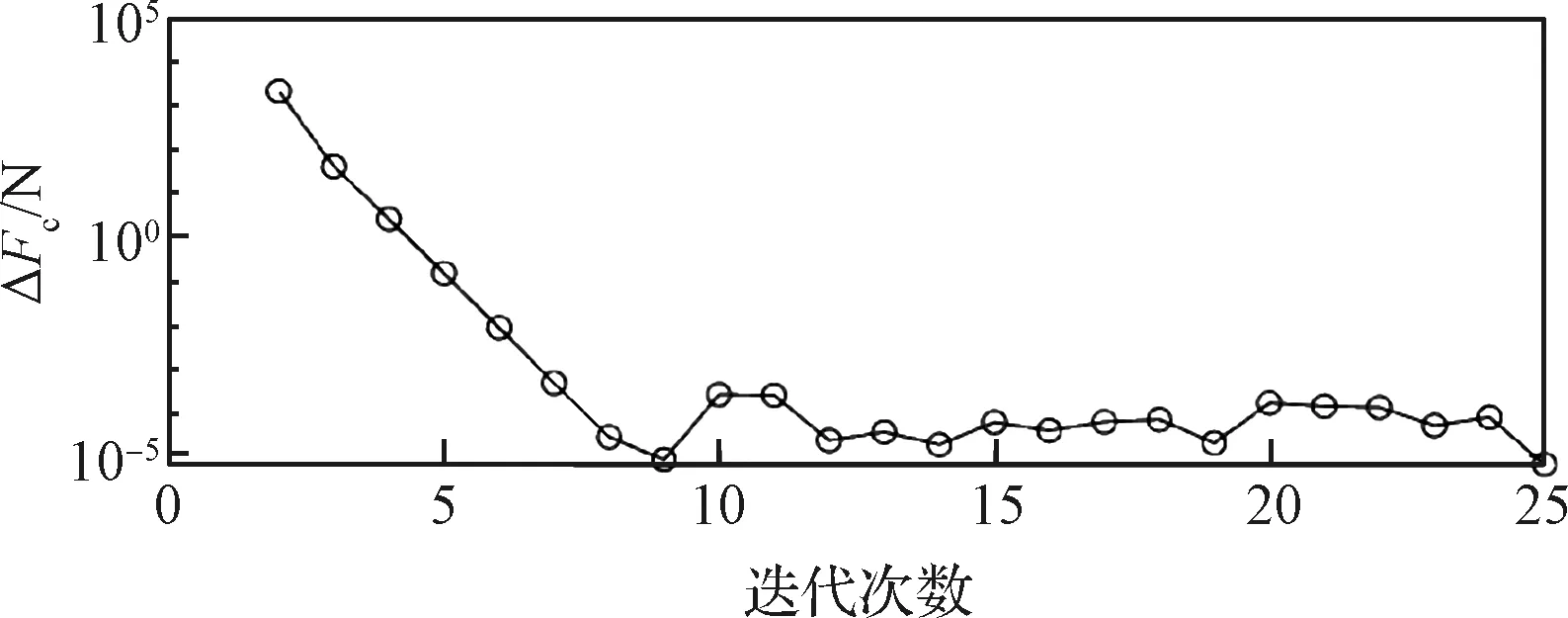
图13 推力指令收敛过程Fig.13 Thrust command convergence process

5 精度分析

为分析本方法精度,考虑轨道转移阶段的制导及定轨精度、点火时间偏差等因素主要影响动力下降段初始位置偏差。因此,本文确定一定的位置偏差作为初始条件进行1000次蒙特卡洛打靶仿真验证。各工况初始偏差设置如表2所示。

表2 着陆器初始位置偏差Table 2 Lander initial position deviation

初始位置在径向上的分布满足：

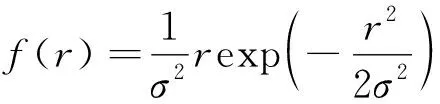
(32)

各工况下着陆器初始的位置误差分布如图14所示。

图14 着陆器初始位置误差分布Fig.14 Initial position error distribution of the lander

仿真结果如图15所示,关于着陆器精度具体的统计结果见表3。其中高度、垂直速度和水平速度这三个指标决定了着陆器是否能够实现安全的月面软着陆；落点分布则展示了着陆器着陆精度。图15(a)为各个工况下最终高度散布情况,由图可以看出,最终的高度误差分布基本符合正态分布；且初始误差越大,最终的高度误差也越大,但即使对于工况3这一最恶劣的情况,最终的高度误差也不超过±3.147 m；图15(b)与(c)分别表示各工况下的垂直速度分布和水平速度分布,可以看出垂直速度误差和水平速度误差分别在0.036 m/s与0.003 m/s以内。以上结果表明,即使当初始误差为±2500 m时,序列凸优化制导算法仍然能够使着陆器在动力下降段完成时达到预定的高度和速度,从而顺利衔接姿态调整段,实现安全着陆。图15(d)为最终落点示意图,由图可知在三种工况下着陆器动力下降段落点误差分别为0.8670 m,2.5336 m,3.6655 m。上述仿真结果表明,当初始位置误差在±2500 m的范围内时,着陆器能够达到预定的位置,实现高精度月面动力下降。

表3 着陆器末状态精度统计Table 3 Precision statistics of the lander in its final state

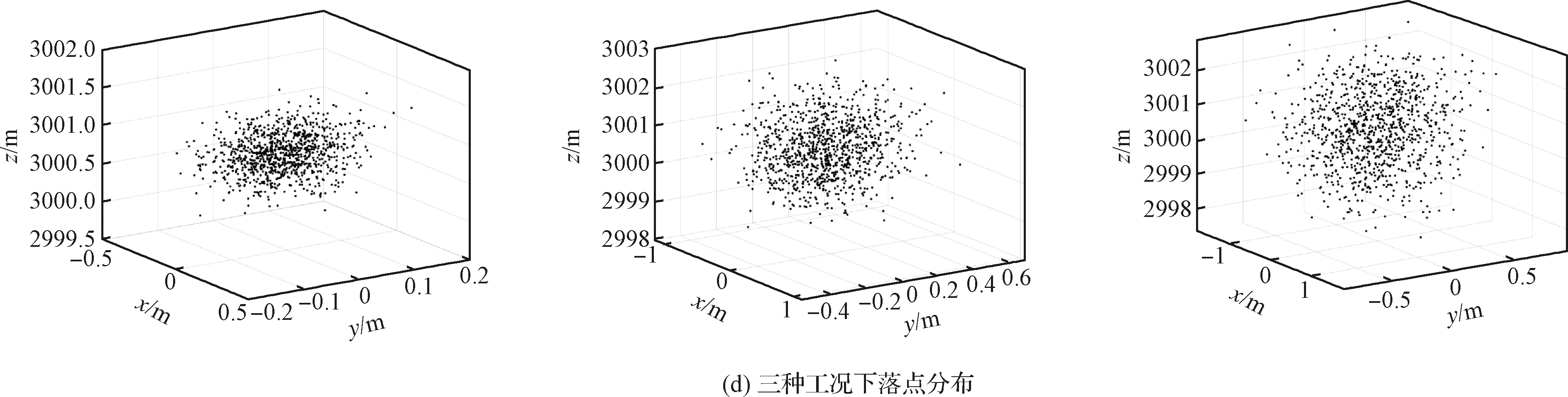
图15 最终误差分布及落点情况Fig.15 Distribution of the final errors and landing points

6 结 论

本文针对传统优化算法应用于月面着陆制导时,时变惯性加速度和重力加速度难以估计补偿问题,提出了一种基于改进序列凸优化的在线制导方法。在考虑月面曲率及月球自转的前提下建立了月面着陆器动力学模型；首先对该模型和约束条件进行凸化,得到一个SOCP问题；并通过逐次进行序列凸优化对动力学模型中难以精确估计的时变加速度项进行迭代优化,直至收敛。在此过程中,时变加速度被同伦地添加到该问题中进行序列迭代求解,使得存在时变加速度扰动时,着陆器仍能在节约燃料的同时实现高精度着陆。仿真结果表明,相比于经典的显式制导律,序列凸优化算法所消耗的燃料更少,相比于经典的伪谱法,序列凸优化算法的计算效率更高。针对不同初始位置偏差的蒙特卡洛打靶结果表明,着陆器初始位置误差即使高达±2500 m,着陆器的末状态速度精度依然在±0.037 m/s以内,位置精度在±3.6655 m内。综上所述,基于序列凸优化的在线制导算法能够高精度地完成动力下降制导,使着陆器能顺利地衔接姿态调整段,实现高精度安全着陆。