基于分解和超平面拟合的进化超多目标优化降维算法

刘海林 肖俊荣

(广东工业大学应用数学学院 广州 510520)

1 引言

在自然科学和工程实际问题中，经常会出现多目标优化问题。当目标个数大于3时，通常称该问题为超多目标优化问题。随着大数据的广泛应用，出现超多目标优化的情形将会越来越普遍[1-7]。目标的增多可能会存在目标之间不一定都是互相冲突的，其中可能存在一些目标与其它目标是正相关关系，这些目标对求解该问题的前沿界面 (Pareto Front,PF)是不必要的，称为冗余目标。如果能找出这些冗余目标，把它剔除，就可使求解的超多目标优化问题得到极大的简化[1,8-11]。将冗余目标从超多目标优化问题中剔除的过程称为目标降维[12,13]。在目标降维研究领域，已有的算法主要分为下面两种类型：

(1) 基于支配关系的算法。具有代表性的是[10]，该算法先用多目标进化优化算法求得一组PF近似解，再利用这组解之间的支配关系，剔除那些对整体支配结构影响较小的目标。PCSEA[8](Pareto Corner Search Evolutionary Algorithm)是该类型另一个较知名的算法，与其它降维算法不同的是，PCSEA是先用多目标进化优化算法找出所有的corner解，再利用这些corner解来判断是否有冗余目标。然而，PCSEA只能处理部分类型的目标降维问题，有些情况无法处理，这点在该算法的论文中也有提到。

(2) 基于相关关系的算法。该类算法一般是先运行多目标进化优化算法求得问题的一组PF近似解，再根据这组解反映出的目标之间的相关信息来找出冗余目标。这类算法具有代表性的有文献[14]提出的算法L-PCA, L-PCA可以处理PF为线性的目标降维问题，但在处理一些PF为非线性的目标降维问题时遇到了困难。为了解决该问题，Saxena等人[1]提出了算法MVU-PCA，MVU-PCA利用了流形学习中的算法MVU (Maximum Variance Unfolding)，把在几何上非线性的PF转化为线性的PF，再采用L-PCA的方法进行目标降维。MVUPCA在处理一些PF非线性的目标降维问题时有了一定的效果。L-PCA和MVU-PCA可以较好地处理一些目标与单个目标正相关导致冗余的目标降维问题，例如测试问题DTLZ5(I, m)[1]；对于目标与多个目标存在多元相关关系导致冗余的目标降维问题则难以处理，例如测试问题MAOP(I, m)[9]。

文献[15]提出了一种不同于上述类型的目标降维算法，该文设计了一种用超平面拟合的算法，提出了算法LHA和NLHA[15]。该方法利用多目标进化优化算法求得PF的一组近似解，再用一个超平面去拟合这组近似解，从而判断出哪些目标是冗余的。该方法简单、高效，不仅可以处理冗余目标与单个目标正相关，还能处理冗余目标与多个目标线性组合正相关的目标降维问题。遗憾的是，LHA在处理PF为非线性的降维问题时易出错，这点在LHA处理测试问题集MAOP(I, m)中有反映出来；而NLHA是通过一种目标的幂变换，来使非线性的PF映射到新的目标空间中靠近某个线性超平面，再用超平面拟合的方法进行降维。遗憾的是，NLHA的处理方法只能把少部分类型的PF线性化，在复杂形状的PF情况下，仍难以达到有效的降维效果。由于在实际问题中，非线性的PF更加常见，因此，在基于超平面拟合方法的基础上，找到一种新的技术来处理PF为非线性的目标降维问题具有重要的意义。

本文提出了一种基于分解和超平面拟合的目标降维算法(Decomposition and Hyperplane Approximation, DHA)。该方法利用“以直代曲”的思想将几何上非线性的PF近似解集分解为多个近似线性的PF近似解子集，通过构建的带扰动项的稀疏超平面拟合的数学模型，找到一个最优的综合超平面去拟合这些子集，最后根据该超平面提取出原问题的本质目标集。相比于LHA, DHA可以更好地处理PF为非线性的目标降维问题；相比于NLHA,DHA在处理非线性的PF时注重的是局部，通过放大局部特征，可以更好地把握目标间的冲突关系，具有更好的稳定性。

本文第2节简单地引入目标降维问题的一些相关概念；第3节将详细介绍本文提出的目标降维方法DHA；第4节将对本文提出的算法DHA进行实验，并与其它有代表性的目标降维算法进行对比；第5节是对本文所做工作的总结。

2 目标降维问题的相关概念与基于超平面拟合的目标降维算法简介

2.1 目标降维问题的相关概念

一个多目标优化问题可以表示为下面的式子：

2.2 基于超平面拟合的目标降维算法介绍

3 基于分解和超平面拟合的目标降维算法

3.1 基本思想与模型的构建

当多目标优化问题的PF呈非线性时，采用基于超平面拟合的降维方法可能难以达到去冗余效果。例如，一个3个目标的多目标优化问题，种群进化到后期呈现如图3所示情形。从图中可以看出目标f1和 目标f2是 相互冲突的，f2与f3呈正相关关系，因此f3和f2中之一可作为冗余目标去除。按照基于超平面拟合的降维算法，则需拟合出平行于f3或f2的平面，才可达到去冗余效果。而当种群处于图3的情形时，它的最优拟合超平面很可能是图3中的蓝色平面，该平面的截距均大于0，依此超平面无法发现冗余目标f3。 实际上，由于f3是冗余的，因此它对于种群中的每一部分来说都是冗余的。假设将图3所示的种群分解为3个子种群，如图4的红色、绿色、蓝色实心圆所示，去除f3对每个子种群内个体的支配关系都不影响，即f3对于每个子种群来说都是冗余的。由于子种群的分布相对于整个种群通常更接近于线性的，因此从子种群更容易拟合出平行于冗余目标的平面，达到去冗余的效果。

图1 目标均非冗余时超平面拟和种群示意图

图2 存在冗余目标时超平面拟合种群示意图

图3 用超平面拟合非线性的种群分布的示意图

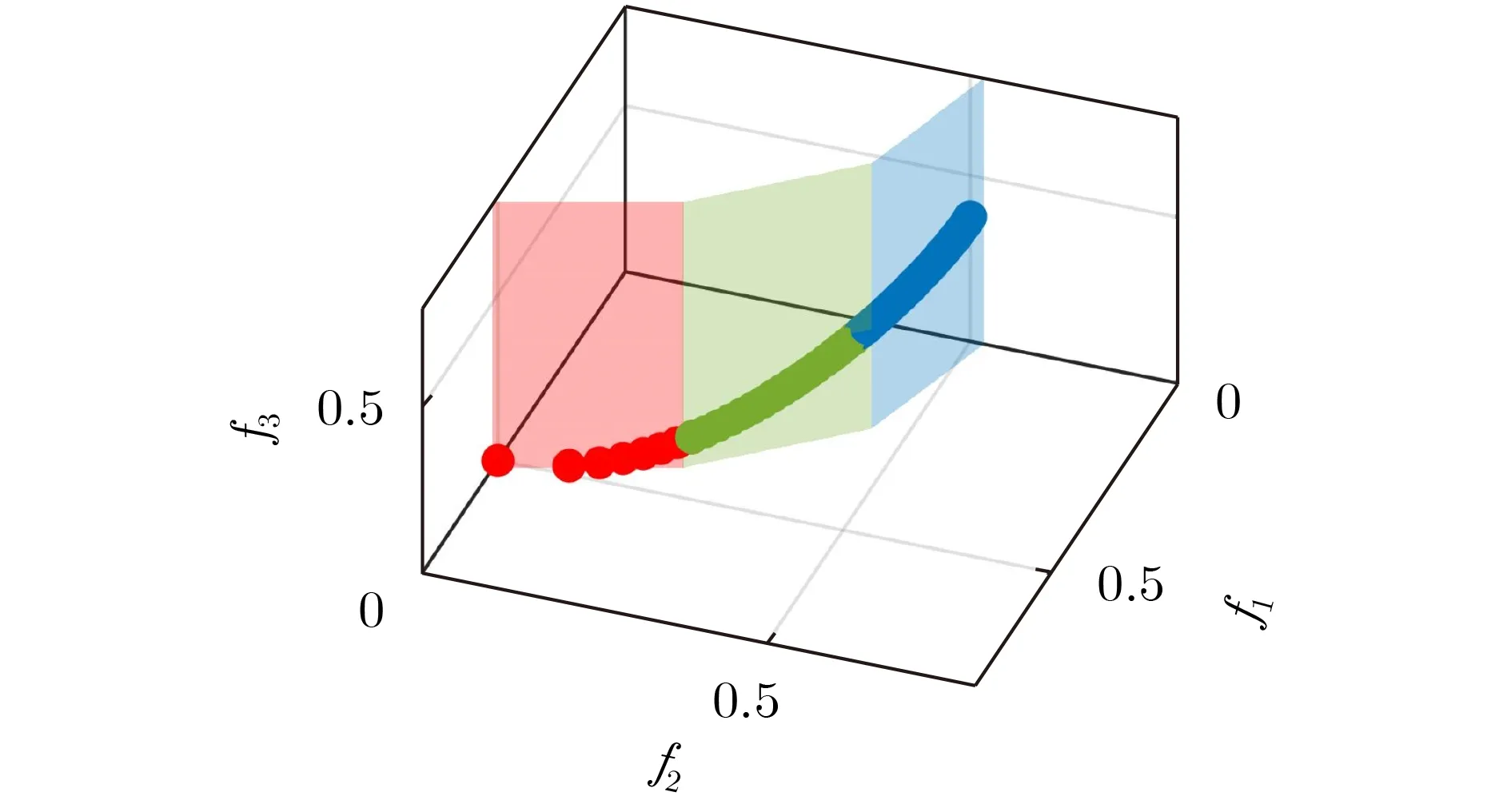
图4 多个平面拟合非线性种群分布示意图

另一方面，应该考虑的是分解后对子种群采用超平面拟合的方法会不会把本质目标错当冗余目标去除。实际上，由于子种群跟整个种群的冲突关系是不一定等价的，因此存在一些情况可能会导致过度降维。该情况是：当某个目标对于整个种群来说是不可或缺的，但它对于每个子种群来说又是冗余的。我们认为出现这种情况是比较少的。对于大多数情况来说，本质目标至少对PF的某个部分来说是不可或缺的，一旦缺失会改变相应部分个体之间的支配关系。

因此，针对非线性的PF，本文将种群分解为多个子种群，用基于超平面拟合的方法从子种群中提取冗余目标，达到更好的去冗余效果。为避免从不同子种群提取出不同的本质目标集，本文采用单一超平面加一些细微的系数扰动来拟合所有子种群，最后用该超平面反映的冲突关系作为提取结果。

根据上面的讨论，本文提出了DHA的数学模型：

3.2 一种基于角度的分解策略

该分解方法既考虑了子种群中心的分布性又考虑了子种群内个体的聚集性，既反映种群总体的特征，也反映它的局部特征。因此，该分解方法可以较好地保留种群携带的信息。

3.3 目标降维算法框架

本节提出两个算法框架，分别是在线的(表1)和离线的(表2)进化目标降维算法DHA框架。

在表1的步骤2中调整MOEA/D-M2M的权重向量是因为基于分解的算法在获取初始权重向量时是在单位超立方里布点的，对于PF取值范围差距很大的问题，若不调整权重向量的尺度，将导致后续再次进化时获取的解集的分布性较差，该策略在文献[15]有详细介绍。在表1的步骤3和步骤5分别是对问题的第1、第2次目标降维。将相应的种群输入到离线的DHA中(表2)，DHA根据3.1节所述的原理和数学模型进行降维，具体步骤在表2中。在第2次降维后若没有目标减少，则认为已找不到冗余目标并

表1 在线的进化目标降维算法DHA

表2 离线的目标降维算法DHA

4 实验设计与实验结果

4.1 评价指标

评价算法的性能需要恰当的评价指标。本文采用文献[15]中使用的成功率指标和σ∗指标。其中，成功率是指在某个问题中成功提取本质目标集的概率，在计算时用对问题成功提取本质目标集的次数除以总运行次数。对于σ∗指标，它的定义式为

4.2 参数设计

为了展示本文所提算法的效果，本文选择了几个有代表性的降维算法作为对比算法：基于相关关系的L-PCA和NL-MVU-PCA；基于支配关系的greedyδ-MOSS和PCSEA；基于超平面拟合的LHA和NLHA。对比算法的参数大小均设置为原论文设置的大小，如表3所示。

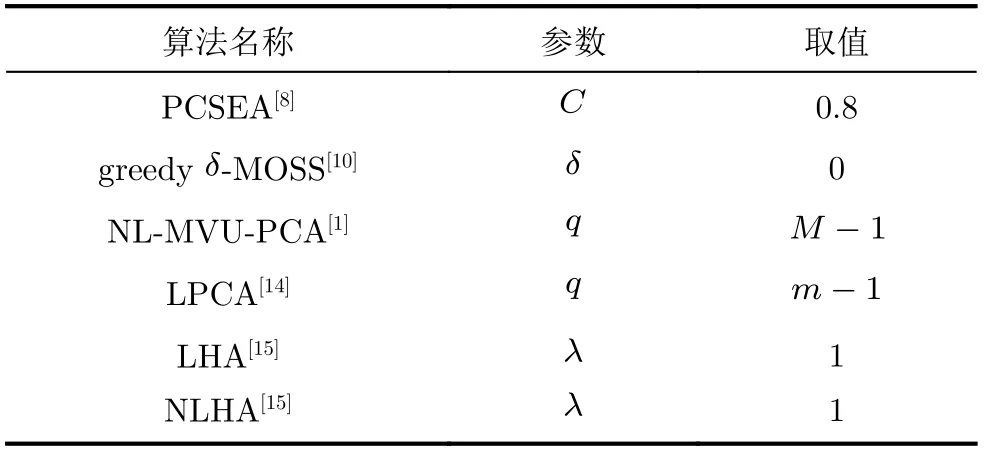
表3 降维算法参数表

为了检测算法的效果，测试函数是必不可少的；本文采用了3个常用的目标降维算法测试函数集：

对于实验数据的获取分为无噪声和带噪声两种情况，无噪声指从问题的真实PF中获取数据；带噪声指未从PF取点，用多目标进化优化算法运行一次代数后的PF近似解集。近似解集中可能含有一些未收敛到真实PF的点，这些点称为噪声点。由于DTLZ5(I,m)和MAOP(I,m)是相对容易收敛的测试函数，因此本文对其获取带噪声时的数据；而WFG3(I,m)是一个难以收敛的测试函数集，本文只测试它们在真实PF取点(无噪声)的情况。

4.3 实验结果与分析

对于测试问题DTLZ5(I,m)。从表4、表5可以看出，本文提出的算法DHA与其他算法相比，具有较高的稳定性。对于LHA, PCSEA在个别问题上的表现不佳，从表5显示它们存在个别σ∗值为0的情况，这反映着它们对应问题上没有去冗余效果。LHA, NLHA它们在DTLZ5(2, 50)的成功率较低，而σ∗值却较高，这显示了虽然它们有不错的去冗余效果，但很多时候不能完全去冗余。而本文DHA在该问题上的两个指标值都稳定且较高，这反映着DHA在个别情况下优于LHA, NLHA。

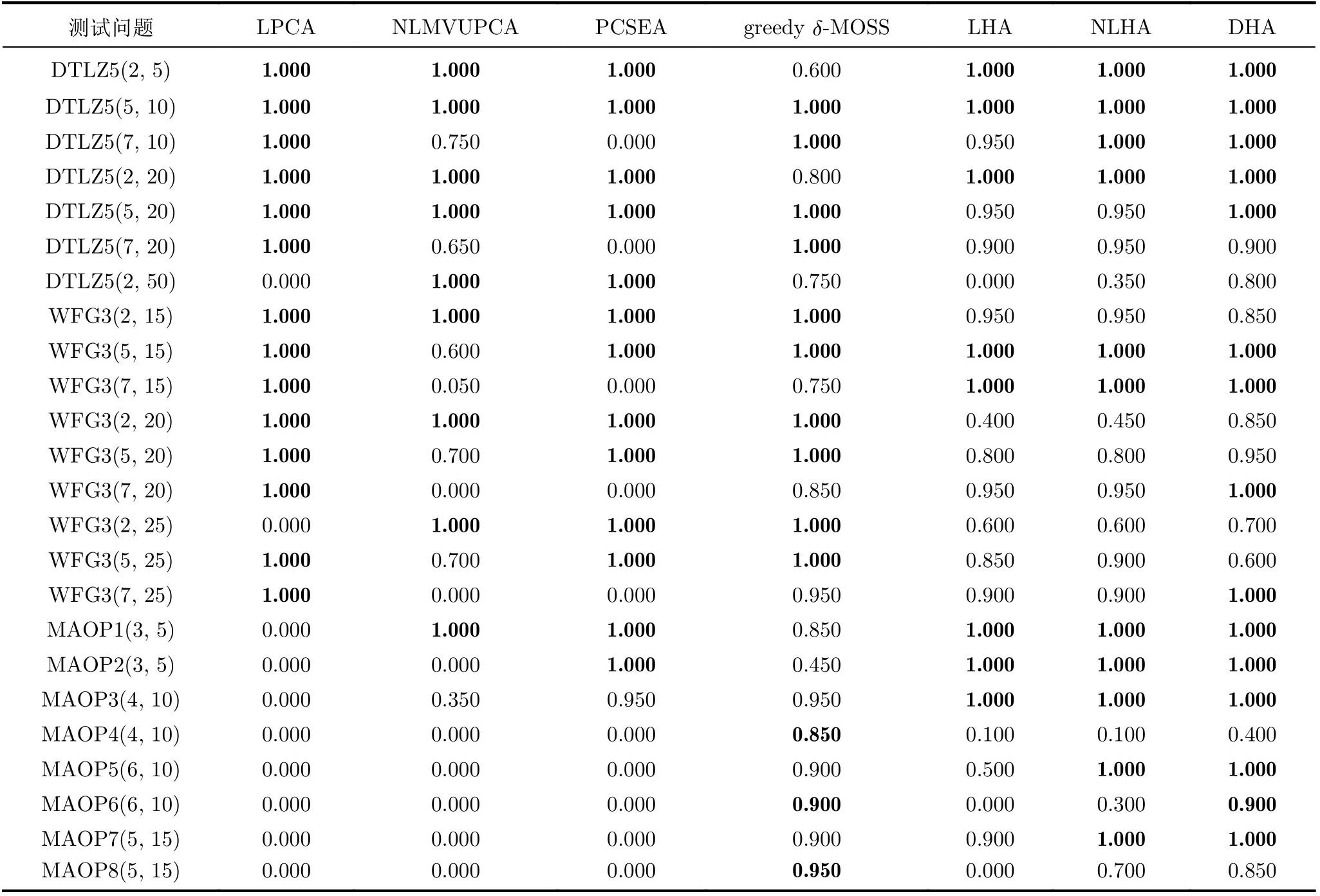
表4 各算法在DTLZ5(I, m), WFG(I, m), MAOP(I, m)问题上的降维成功率

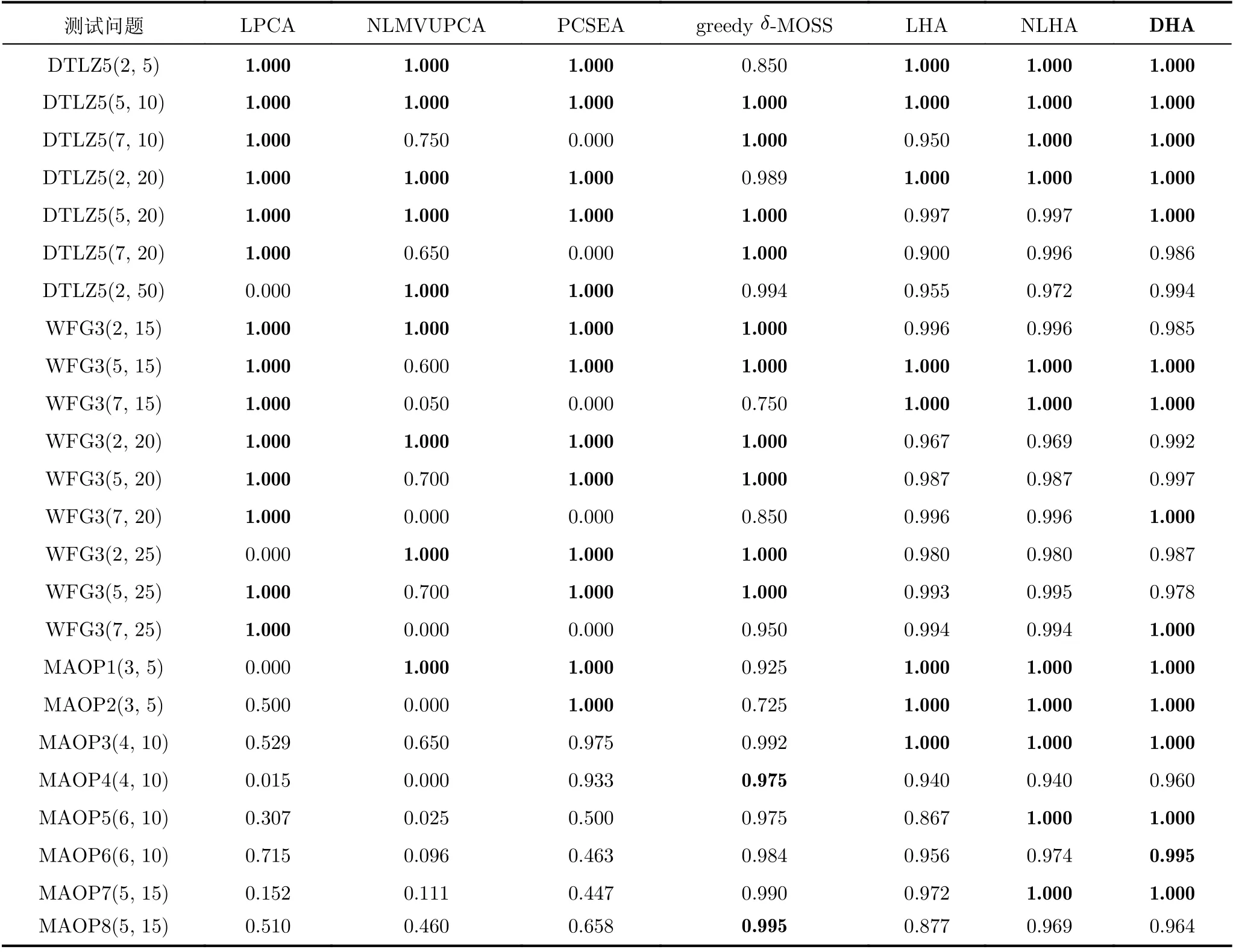
表5 各算法在DTLZ5(I, m)、WFG(I , m)，MAOP(I, m)问题上的的平均σ ∗值

对于测试问题集WFG3(I,m)，它是一个PF为线性的测试问题集。从表4和表5可以看到，DHA对每个测试情况都能较好地处理，而对于算法LPCA, NLMVUPCA, PCSEA存在个别成功率和σ∗值都为0的情况，即没有降维效果。对于算法LHA,NLHA也能较稳定地处理每种情况。对该测试问题，由于PF是线性的，DHA对于LHA和NLHA没有明显的优势，但也反映了DHA能较好处理PF为线性的带冗余目标的超多目标优化问题。

MAOP(I,m)中的冗余目标不是跟单个目标正相关，而是与多个目标存在多元相关关系，这大大地增加了目标降维的难度。从表4和表5可以看出，LPCA, NLMVUPCA对该问题的大部分测试情况的成功率和对应的σ∗值都较低，效果较差。PCSEA只能较好地处理前4种情况，对于后面4个测试情况效果较差。其它4个包括DHA可以较好地处理该问题。从greedy-δMOSS在MAOP2(3, 5)的测试结果看到，该算法也存在一些情况不稳定的，受到了噪声点的干扰。对于LHA和NLHA, DHA在MAOP4(4, 10)和MAOP6(6, 10)上有些许优势。LHA和NLHA在这两个测试函数的成功率较低而σ∗值却较高，这是因为他们去冗余效果不错，但最终找出本质目标集的情况却不多，而DHA在这两方面都较好。

5 对DHA的进一步探究

5.1 DHA对进化算法的作用分析

为探究DHA在实际进化过程中起到的效果，本文将施加DHA的MOEA/D-M2M记为DHAMOEA/D-M2M与未施加DHA的MOEA/D-M2M对超多目标优化问题求解效果进行对比实验，用传统的反转世代距离[18](IGD)作为评价指标。IGD的定义为

将DHA-MOEA/D-M2M与MOEA/D-M2M在测试问题DLTZ5(5, 10)，DLTZ5(2, 20)，DLTZ5(5, 20)进行实验，两个算法均运行600代后停止，对于前者在进化300代后调用DHA进行1次目标降维。对实验的其它参数设置同第4节。对每个问题独立运行20次，计算IGD值，实验结果如表6所示。

从表6可以看到，除了MAOP1(3, 5)，其它运行结果均有明显的提升。这反映了在进化过程中使用DHA进行目标降维，可以有效提高所求解集的质量。

表6 DHA-MOEA/D-M2M与MOEA/D-M2M在各个测试函数独立运行20次的平均IGD值与标准差

5.2 对DHA参数的敏感性分析

DHA需要设置两个参数：子种群个数K和参数λ。在第4节的实验中K设为10，λ设为1。为检验DHA的稳定性，现将K取5个值：6, 8, 10, 12, 14，λ取5个值：0., 1, 1.5, 2, 2.5，两个参数两两配对在测试问题MAOP5(6, 10)上进行实验，计算各自降维成功率，将得到的25个实验结果作3维曲面图，结果如图5所示。从图5可以看到，DHA对子种群数K和参数λ的取值在一定区域内不敏感，通过合适的取值可以使DHA保持较高的成功率。

5.3 种群大小对DHA降维效果的影响分析

对于PF的真实维数较高的超多目标优化问题，若种群个体太少，则可能因难以刻画真实PF的特征导致对问题过度降维的结果。由于DHA是基于种群分解，因此种群大小对DHA的影响会大于其他算法。为探究该影响，本文采用DTLZ5(2, 5),DTLZ5(5, 10), DTLZ5(7, 10)作为测试问题；将每次进化代数G设为固定300；种群大小N分别设为20,30,50,100,200,300,400；其他参数同4.1节的设置。采用在线的DHA框架，对每个问题独立运行20次，实验结果如图6所示。从图中可以看到当问题的PF真实维数不高时，如DTLZ5(3, 5)和DTLZ5(5, 10)，DHA对种群大小的要求不高，适当的取值均可获得较高的成功率。而对于PF真实维数比较高的问题DTLZ5(7, 10)，此时种群不宜太小，太小则会影响效果。从图6可以看到，当种群大小设为200以上时，DHA对DTLZ5(7, 10)保持了较高的降维成功率。

图 5 DHA对应不同的K , λ 值在MAOP5(6,10)上的降维成功率曲面图

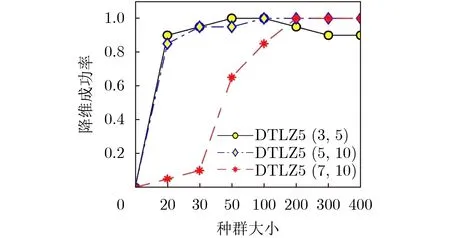
图 6 不同种群大小下，DHA在相应问题的降维成功率变化图

6 结束语

本文提出了一种基于分解和超平面拟合的目标降维算法DHA。在该算法中，种群中的非劣解集基于角度被分解成多个非劣解子集，根据本文构建的DHA的数学模型找到一个综合的超平面结合扰动项来拟合这些子集，进而根据该超平面提取原问题的本质目标集。该算法既可以处理前沿界面分布为线性，也可以处理前沿界面分布为非线性的目标降维问题。为了测试DHA的性能，采用3个常用的目标降维测试问题DTLZ5(I,m), WFG3(I,m)和MAOP(I,m)，并与当前具有代表性的目标降维算法进行对比。计算机仿真结果表明提出的算法无论前沿界面是线性或非线性的情形都具有优异的性能。当前的目标降维算法大都是以进化到一定代数的非劣解集作为近似的PF来找出冗余目标，是否存在一个更好的判断冗余目标的方法，还有待进一步研究。