数控机床二质量伺服系统惯量匹配研究

刘光宗，苏建新，孙亚琼，李洪伟，杨俊涛

(1.河南科技大学机电工程学院，河南洛阳 471003；2.洛阳LYC轴承有限公司，河南洛阳 471039；3.机械装备先进制造河南省协同创新中心，河南洛阳 471003)

0 前言

高速精密磨削加工要求数控机床反应灵敏、精度高、可靠性强，相关研究表明：负载电机惯量匹配对数控机床系统的稳定性、动态响应(如系统超调、上升时间、调节时间)以及机床精度有着十分重要的影响。在实际工程应用中，折算到电机轴的负载惯量与电机的惯量之比不宜过大，应控制在合理的范围内，否则系统会出现振荡甚至失控。相关学者作了大量研究，英国ARMSTRONG[1]和美国MOSCROP等[2]针对伺服系统在负载电机惯性失配情况下的控制进行了学术交流；LI和LIU[3]对负载惯性变化的永磁同步电机系统在速度自适应控制方面进行了研究；SHAO等[4]研究某并联机器人，仿真得出了惯量指标以及合适的惯量匹配范围；黄捷建等[5]总结了在负载惯量与电动机惯量高度不匹配的应用中可采取的应对措施；张彦方等[6]针对重型数控机床给出了直线加工和圆弧加工2种加工形式下较优的惯量比范围；刘辉等人[7]建立进给系统的双惯量模型进行仿真分析，给出了综合考虑各项性能的进给系统负载惯量比设计步骤和方法；杨森[8]通过建立机床虚拟样机的机电联合仿真平台，分析了不同驱动方式和不同加工工况下机床进给系统的最佳负载惯量比；孙成志等[9]建立了转动惯量与质量之间的函数关系，得到了发动机飞轮与电机转子转动惯量的最佳匹配；袁磊等人[10]提出了满足伺服运动系统的定位精度和同步控制精度的方法。但目前可查到的文献中还没有一种可以对伺服系统惯量匹配普遍适用的方法，仍需具体问题具体分析。

1 概述

1.1 惯量匹配含义

对于某特定的伺服电机，若采用减速机构，同时忽略减速机构自身所增加的惯量和效率损失的情况下，使折算到电机轴上的负载惯量与伺服电机的惯量相匹配(负载惯量等于电机惯量，即惯量比为1)，该伺服系统就能实现最佳功率传输，且能获得最大的负载加速度，即所谓的“惯量匹配”。

1.2 惯量匹配原则

图1所示为伺服系统进给结构简图。对于机械传动系统，根据牛顿第二定律可知：

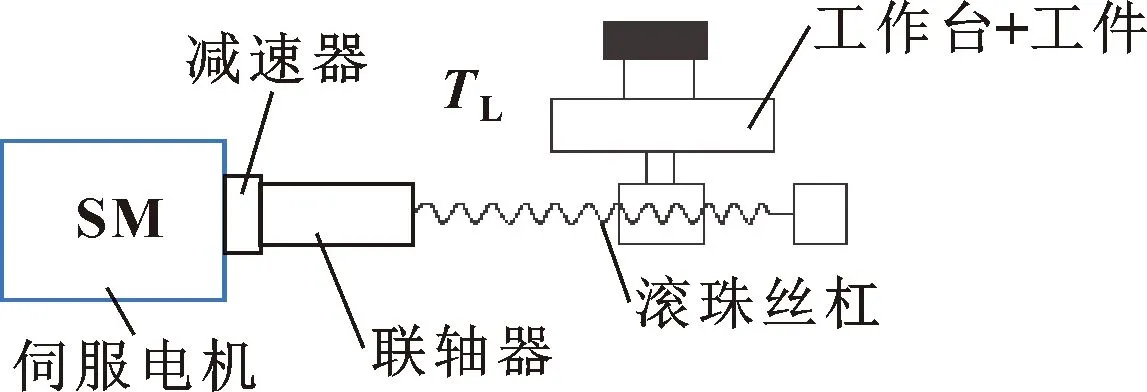
图1 伺服系统进给结构简图

2π(Jm+JL)dn/dt=Tm-TL

(1)

式中:Jm为伺服电机自身惯量(kg·m2)；JL为折算到电动机轴的负载惯量(kg·m2)；n为电机转速(r/s)；t为加减速时间(s)；Tm为伺服电机转矩(N·m)；TL为折算到电机轴的负载转矩(N·m)。2πdn/dt为角加速度，角加速度越小，则数控系统从发出指令到指令执行完毕所需时间越长，即通常所说的系统反应迟钝；相反，则系统反应灵敏。若角加速度变化，即系统反应忽快忽慢，就会影响加工精度。当进给伺服电机选定，则转矩一定，若期望角加速度的变化尽可能小，应使Jm+JL的变化尽量小，Jm+JL越小越有利于调速，瞬态响应就越好。

JL/Jm为负载电机惯量比(为了表示方便，用q表示惯量比JL/Jm)，反映了电机对负载的控制能力。q值越大，则电机控制稳定性越差，动态特性受负载影响越大，越易受其他因素干扰，系统调试困难及定位时间长，加工性能越低；q值越小，则电机惯量占总惯量的比率越大，电机的控制能力越强，动态特性越好，加工性能越好。

根据相关研究，q一般选择范围：q≤5，其中：

(1)对于大型数控机床，q≤5；

(2)对于中小型数控机床，q≤2；

(3)高速高精度特殊加工，q≤1。

对于现代全闭环数控机床，常把高“伺服精度”和优“瞬态响应特性”作为首要追求目标，转矩虽有裕量，但仍以惯量匹配达到最佳状态为目标，这对提高加工精度、减小加工表面粗糙度以及提高加工效率十分有利。因此，应优先考虑惯量匹配，这就是惯量匹配的原则。

2 惯量匹配设计

2.1 伺服系统惯量匹配设计

在摆线轮成形磨齿机数控系统设计中，某型号磨齿机水平方向载质量(工作台+工件)m1约为300 kg、滚珠丝杠(螺距S=26 mm、直径D=80 mm)质量m2约为40 kg、负载与导轨之间摩擦因数μ=0.002，设机械传动效率η=95%，要求负载移动速度v最大达到0.8 m/s，加减速时间t为0.5 s，对该方向伺服电机进行选型设计。

(1)折算到电机轴上的负载惯量为

JL=m1(S/2π)2+m2D2/8=300×(2.6/6.28)2+40×82/8=371.42 kg·cm2

(2)电机驱动负载所需转矩

①电机转速为

n=v/S=60×0.8/0.026=1 846 r/min

②克服摩擦力所需转矩为

T1=μm1gS/(2πη)=0.002×300×9.8×0.026/(2×3.14×0.95)=0.026 N·m

③重物加速时所需力矩为

T2=m1aS/(2πη)=300×0.8/0.5×0.026/(2×3.14×0.95)=2.092 N·m

④螺杆加速时所需转矩为

T3=(m2D2/8)(2πn/60)/(tη)=(40×82/8/10 000)×(2×3.14×1 846/60)/(0.5×0.95)=13.74 N·m

由②③④知，所需最大转矩为

T=T1+T2+T3=15.86 N·m

根据(1)(2)知，伺服系统负载惯量为371.42 kg·cm2、电机驱动所需最大转矩为15.86 N·m，则可选额定转速2 000 r/min、额定力矩16 N·m、转子惯量75 kg·cm2的伺服电机。其负载电机惯量比为371.42/75≈4.95，符合惯量匹配原则。

2.2 伺服系统惯量匹配优化方案

为减小惯量比不匹配对系统造成的不利影响，提出以下改善策略:

(1)提高机械系统刚度，这需要在机床组装前选择刚度较好的零部件；

(2)采用合适的减速机构，使惯量不匹配程度降到最小；

(3)增加伺服电机惯量，提高伺服电机对系统的控制能力以及系统稳定性；

(4)采用双轴伺服同步控制代替传统单轴驱动控制，在同等惯量情况下，可提高系统动态性能；

(5)构建伺服驱动闭环PID控制系统，实时检测、调节并跟踪系统位置和转速，获得更快、更稳的瞬态响应。

3 二质量伺服系统动力学模型及仿真实验

为验证惯量匹配效果，结合上述优化方案(5)，引入二质量伺服系统概念，构建二质量伺服驱动闭环PID控制系统并进行仿真研究。

3.1 二质量伺服系统

如果把伺服系统中电机与负载作为一个刚体来考虑，则该系统称为单质量伺服系统。对于实际系统，尽管电机与负载是直接耦合的，但传动本质上是弹性的，在电机驱动力矩的作用下，机械轴会受到某种程度的弯曲和变形作用。对于加速度大、快速性和精度要求高的系统，弹性形变对系统性能的影响不能忽略。在定性计算时，通常将传动轴的转动惯量Ja计入到JL中，因此可将电机传动系统简化成电机-负载组成的二质量伺服系统模型，如图2所示。

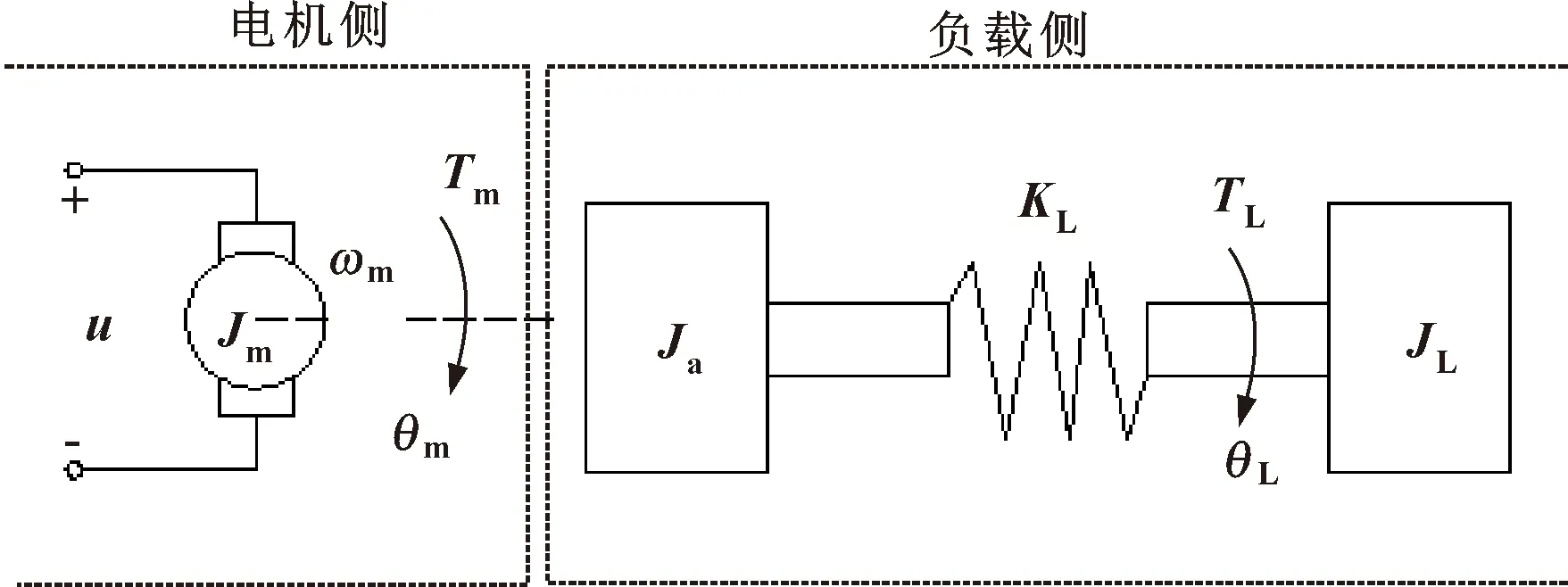
图2 二质量伺服系统模型

其中：u为电源电压；θm和θL分别为电机转角和负载转角；Tm和TL分别为电机力矩和负载转矩；Ja为传动轴转动惯量；KL为耦合刚度系数。

3.2 伺服驱动闭环PID控制系统模型

3.2.1 伺服电机控制模型

根据图3，可得电机电力学方程：

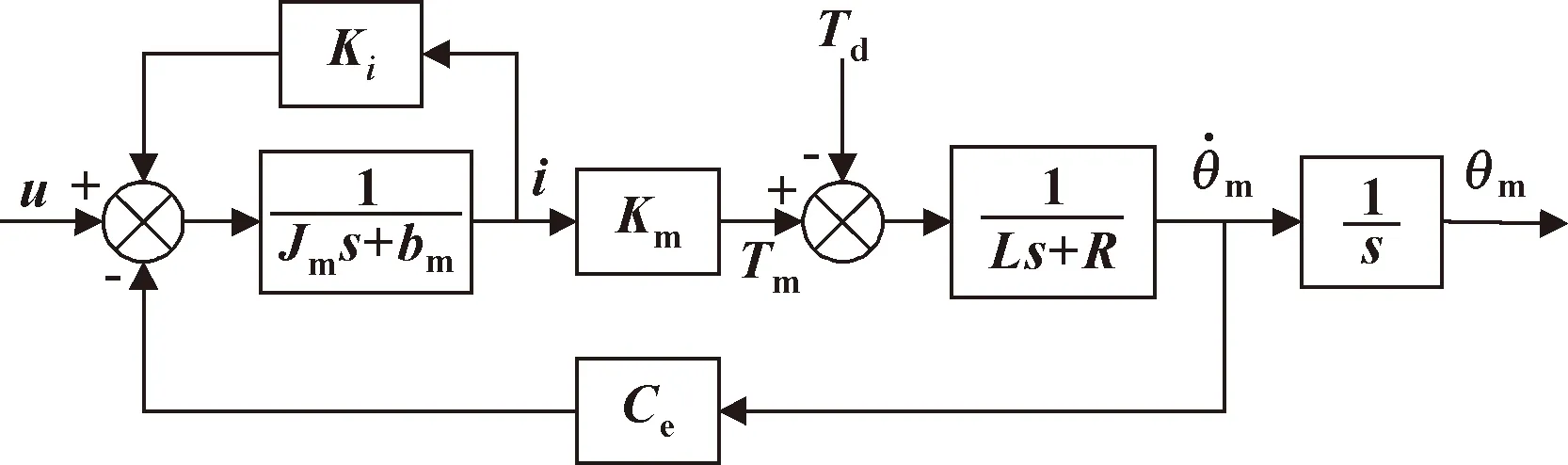
图3 伺服系统电机框图

(2)

其中：L为电枢电感;R为电枢电阻;Ce为电动机反电动势系数;Ki为电流反馈系数;Km为电机力矩系数;Jm和JL分别为电机的转动惯量和负载的转动惯量;Td为扰动力矩;bm为电机黏性阻尼系数。

3.2.2 负载模型

根据图4，可得负载动力学方程为

图4 负载框图

(3)

由式(2)(3)，可得负载电机惯量比为

q=JL/Jm=

(4)

由上述电机及负载结构框图，建立电机-负载二质量伺服系统结构框图，如图5所示。

图5 二质量伺服系统结构框图

3.3 伺服驱动闭环PID控制系统模型

根据图3，在Simulink环境下搭建电机仿真模型如图6所示。

图6 闭环PID控制Simulink主模型

为使仿真系统搭建简化，提前将上述搭建好的电机模型进行封装，以便随时调用。进而在Simulink环境下搭建二质量伺服系统仿真模型，如图7所示。

图7 Simulink环境下二质量伺服系统模型

然后，在Simulink环境下搭建二质量伺服PID控制系统仿真模型如图8所示。为进一步简化，再将建立的二质量伺服PID系统仿真模型作为一个整体被控对象进行封装，便于调用。搭建控制系统主模型时，通过PID控制器输入信号直接连至整体封装模型。其中，PID控制器内部结构如图9所示。

图8 闭环PID控制Simulink主模型

图9 PID控制器Simulink内部结构图

图8中被控对象是一个二质量伺服系统。输入正弦波y=sin2πt，控制器采用PID控制(取PID控制器参数kp=8、ki=1、kd=5)进行仿真。仿真时，通过改变负载惯量，使q取不同的值，分别为1、3、5、7、9，跟踪系统的位置和速度响应，结果分别如图10和图11所示。

图10 不同惯量比下的位置跟踪 图11 不同惯量比下的速度跟踪

由图10、图11可知:在惯量比小于等于5时，系统位置和速度响应效果较好，且惯量比为1时达到最佳；随着惯量比的增大，无论系统位置跟踪还是速度跟踪响应均有所滞后，且随之增大。系统动态性能变差，比值过大时会出现位置平顶和速度死区现象。

4 结束语

惯量匹配在数控机床的进给系统设计中很重要，尤其是对于动态性能和稳定性要求较高的场合。通过摆线轮成形磨齿机数控化设计实例进行了定量计算和分析，构建了二质量伺服驱动闭环PID控制系统模型，并进行了MATLAB仿真，分析了不同惯量比情况下位置和速度跟踪结果，结果表明：

(1)惯量比q≤1时，系统位置和速动跟踪趋近于理想曲线，几乎同步运动，可以满足精密零部件加工需求；

(2)惯量比1

(3)惯量比3

(4)惯量比5

(5)惯量比q>7时，系统动态性能变差，尤其是当q≥9时，系统动态特性急剧下降，不仅会发生位置平顶现象，还会发生速度死区的现象，造成跟踪失真。反映在机床具体运动时，会出现动作响应较慢，且动作不能按照给定输入执行到位，无法满足正常加工需求。