矿用自卸车驱动车桥的桥壳结构优化

孙远敬，郭 鹰，李 鑫，王 帅

（辽宁工程技术大学 机械工程学院，辽宁 阜新 123000）

0 引言

汽车轻量化是在保证汽车的强度和安全性能的前提下，尽可能地降低汽车的整车质量[1].实验表明，汽车的整车质量每降低 10%对应燃油率提高6%～8%[2].因此汽车进行轻量化对汽车行业来说是最有效的途径之一.

郝妮妮等[3]研究了基于遗传算法的重型矿用自卸车车斗优化设计，实现了优化后矿用自卸车车斗减重9.6%、柴油节约8%，验证了尺寸优化对矿用自卸车的轻量化设计问题的有效性.李秋琴[4]研究了矿用自卸车驱动桥壳力学及模态特性，使桥壳得到了更高的强度，质量分布也更加合理.

选取了某55 t级矿用自卸车后驱动车桥的桥壳作为研究对象，在实现桥壳轻量化的同时改善桥壳在特定工况下的受力状态，通过在桥壳多目标优化研究中引入代理模型技术来解决桥壳受力时结构不规则导致受力情况复杂问题.并将其作为后续优化求解的目标模型，实现对矿用自卸车桥壳轻量化设计.

1 桥壳在侧向力工况下的受力分析

矿用自卸车对驱动车桥的强度、刚度要求较高.因此，车桥一般为非断开式驱动桥，桥壳选择使用整体式结构，本次研究的是某55 t级中小型矿用自卸车的后驱动桥壳，该后驱动桥壳的主要参数及原始几何模型见表1、图1.自卸车左转时的驱动桥壳受力见图2.

表1 某55 t级矿用自卸车的整车参数Tab.1 vehicle parameters of a 55 t dump truck for mining

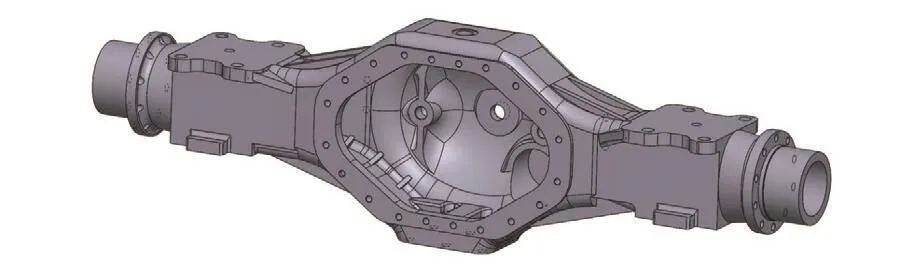
图1 桥壳的原始几何模型Fig.1 original geometric model of the axle housing

汽车转弯时，汽车质心处会产生离心力Fy，导致汽车轮胎中心产生侧向力，与之对应的地面也会产生对轮胎的侧向反作用力，称为侧偏力Fy，如图2中的Fyl和Fyr.当地面侧向反作用力Fy超过车轮与地面的附着极限时，车轮发生侧滑[5].

对于两侧车轮有

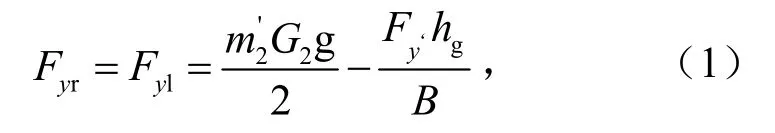
式中，Fyr为地面对外侧轮胎的侧向反作用力，N；hg为自卸车满载时质心高度，取 1.82 m；Fy'为急转弯时自卸车质心处离心力，N.

假设汽车在最高时速下转弯即将发生侧滑的状态，此时Fy'为

式中，V为转弯车速，km/h；G2后驱动桥满载载荷，N；为负载转移系数，取 1.25；Rm为自卸车最小转弯半径，取1.88 m.

此时,桥壳右侧即外侧板簧座危险断面垂直平面所受弯矩Mvr和弯曲应力δr为

式中，rr为车轮半径，取0.42 m；Fzr为地面沿对右侧轮胎施加的垂直反力，N；b为轮胎中心平面到板簧座之间的横向距离，m；φ为侧滑时地面与轮胎间的附着系数；ωv为危险断面处垂直平面的抗弯截面系数.

桥壳左侧即内侧板簧座危险断面垂直平面所受弯矩Mvl和弯曲应力δl为

式中，Fzl为地面沿对左侧轮胎施加的垂直反力，N.

桥壳外侧板簧座危险断面水平面所受转矩Mhr和扭转切应力rτ为

合应力为

式中，δ为弯曲应力与扭转切应力的合应力，MPa；ωt为桥壳外侧板簧座危险断面处水平面的抗扭截面系数.

由式（9）计算求得右侧弹簧座的危险断面处的合成应力为5种工况中的最大值，但未超过屈服强度350 MPa，后续的桥壳多目标优化设计应以最大侧向力工况为基础进行优化设计.

2 基于侧向力工况下的有限元分析

采用 HyperMesh对矿用自卸车桥壳进行网格划分.考虑侧向力工况下的边界条件，桥壳Mises应力分布见图3.

图3 最大侧向力工况下桥壳Mises应力分布Fig.3 mises stress distribution diagram of axle housing under maximum lateral force condition

由图3可知，在最大侧向力工况下，桥壳承受的Mises应力为318 MPa左右，与计算的侧向力工况下的最大弯曲应力较为接近.在最大侧向力工况下，桥壳变形分布见图4.

图4 最大侧向力工况下桥壳变形分布Fig.4 strain distribution diagram of the axle housing under the maximum lateral force condition

由图4可知，桥壳的最大变形分布在弹簧座内侧部位和主减速器壳附近，最大变形达到了1.04 mm，由相关标准可知该桥壳材料刚度符合相关标准.

3 桥壳代理模型的构建

代理模型是在不降低计算结果精度的前提下，构造的一个计算量小[6]、计算周期短、物理试验结果相近的数学模型[7].而构建代理模型包括以下5个步骤：采集点数据、选择代理模型类型、建立代理模型、验证代理模型、精度检验.

基于桥壳轻量化来建立的多目标优化，选择桥壳的危险断面处的截面厚度X1、宽度X2和高度X3以及桥壳套管X4为设计变量，利用拉丁超立方设计法选择的100个样本点在三维空间内的分布见图5.

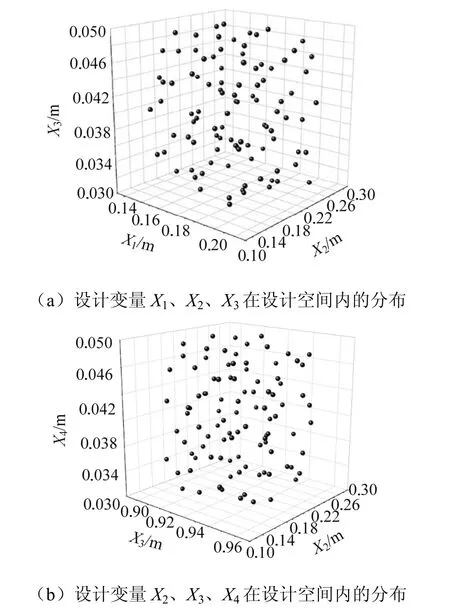
图5 样本点在三维设计空间内的分布Fig.5 distribution of sample points in the three-dimensional design space

试验设计选取的100个样本点经过自动有限元分析过程完成后，部分构建桥壳代理模型的初始样本点的取值与响应见表2.

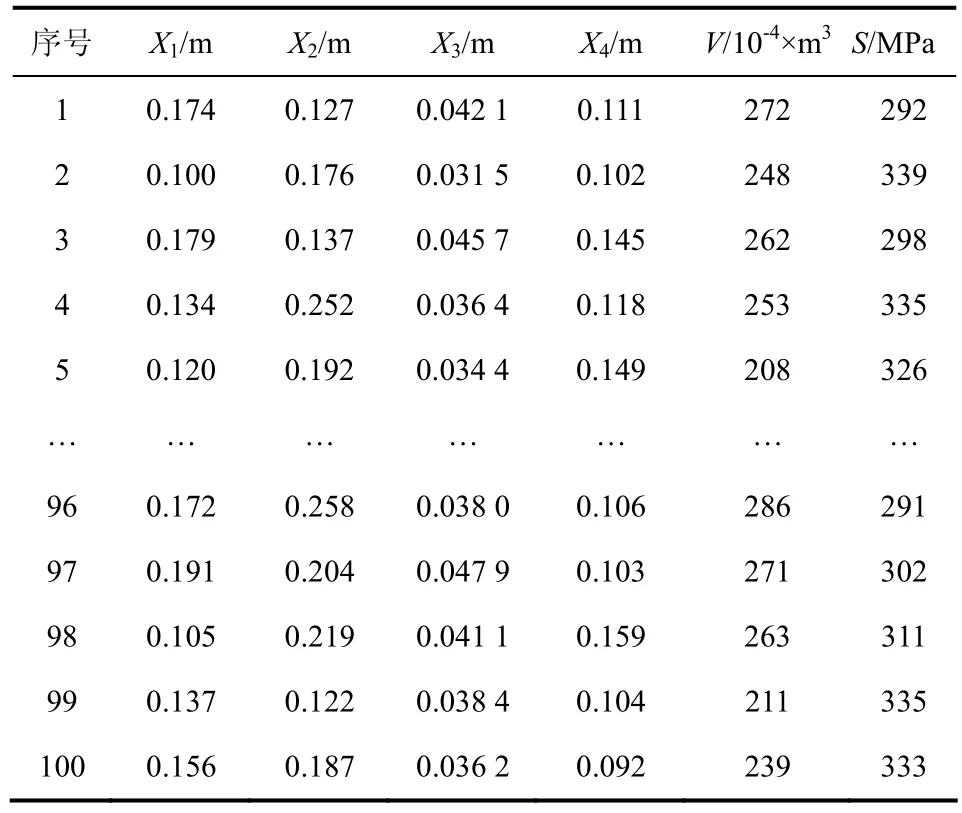
表2 部分试验点仿真结果Tab.2 simulation results of some test points

4 桥壳轻量化设计的多目标优化

4.1 基于桥壳的多目标优化模型的建立

根据矿用自卸车的满载工况时的理论受力分析得此次桥壳的多目标优化过程中的设计变量为

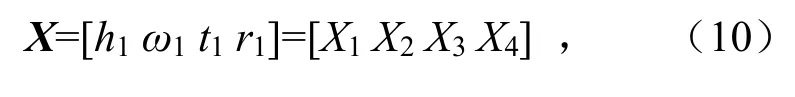
在桥壳材料不变下实现桥壳的轻量化目标可通过减小桥壳体积来实现.以体积最小作为第一优化目标，并利用响应面模型求解最优值.桥壳体积V与部分设计变量之间的响应面模型见图6.

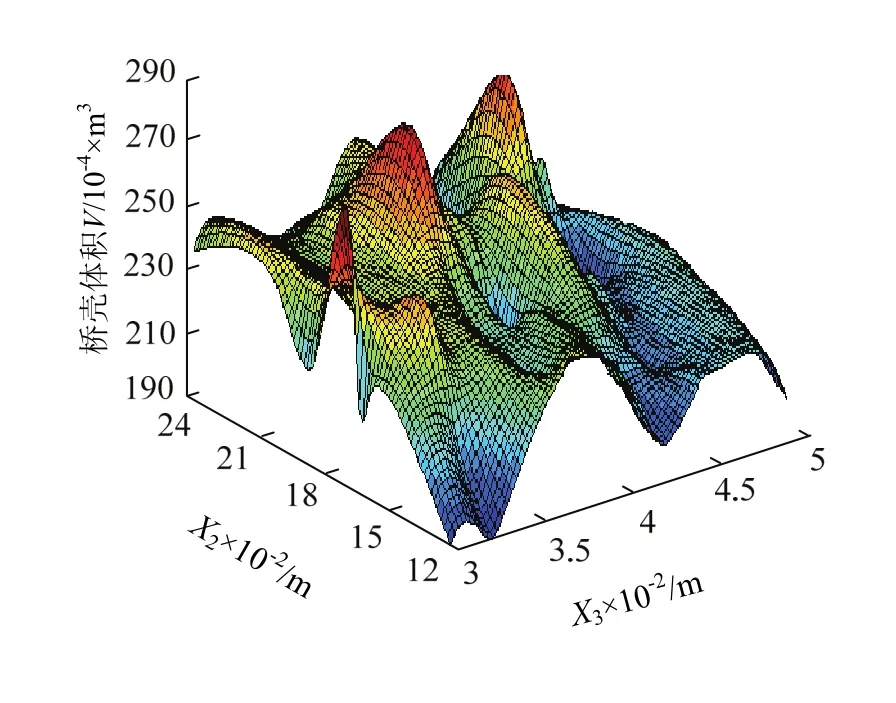
图6 桥壳体积V与部分设计变量之间的响应面模型Fig.6 response surface model between the volume V of axle housing and some design variables

以桥壳在满载、侧向力工况下的 Mise应力作为第二个优化目标，桥壳应力S与部分设计变量之间的代理模型见图7.

图7 桥壳应力S与部分设计变量之间的响应面模型Fig.7 response surface model between bridge shell stress S and some design variables

多目标优化求解中约束条件设置见表3.

表3 桥壳多目标优化问题中的约束条件Tab.3 constraints in the multi-objective optimization problem of axle housing

综上，多目标优化设计的数学模型[8]表达式为

4.2 桥壳多目标优化模型的联合优化

壳响应面模型有较多局部凹陷的问题，选择人工蜂群（ABC）算法作为模型的优化求解策略[9].在Matlab中建立ABC算法模型，而后在组件下的Content模块导入Matlab中建立的改进ABC算法代码.将4个设计变量依次与ABC算法中的自变量进行映射[10].

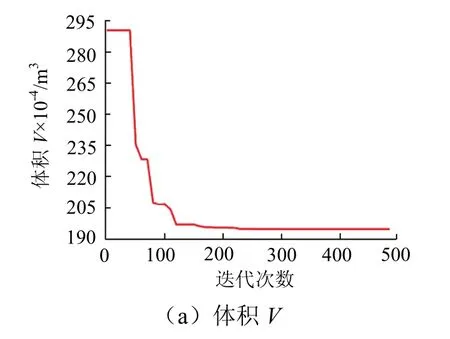
经过500次迭代优化，得到关于体积目标函数和最大等效应力目标函数在整个求解过程中的迭代过程见图8.

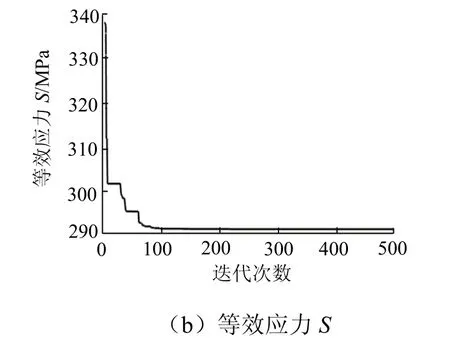
图8 桥壳目标函数的迭代优化过程Fig.8 iterative optimization process of objective function of axle housing

对求得的优化解集进行取整处理，优化结果见表4.

表4 优化解集Tab.4 optimized solution set

5 结论

通过对某55 t级矿用自卸车后驱动车桥的桥壳进行基于轻量化设计的多目标优化设计研究得到以下结论：

（1）通过对桥壳最大侧向应力的分析，发现在最大侧向力工况下，桥壳的最大变形量分布在弹簧座内侧部位和主减速器壳附近.

（2）建立矿用自卸车驱动桥壳的多目标优化模型，采用代理模型技术求解得到设计变量与目标函数的系数矩阵的近似数学关系，并建立设计空间内的目标函数响应面模型.为解决设计变量与目标函数之间没有明确的数学函数关系提供了新的求解方法.

（3）结合Matlab建立人工蜂群算法针对桥壳代理模型进行优化求解.成功实现了Isight和Matlab对桥壳代理模型的联合优化.最终证实该款 55 t级矿用自卸车后驱动车桥的桥壳在体积减小 18.75%的同时，在满载最大侧向力工况下受到的最大等效应力下降7.23%.