融合LSTM和优化SVM的风力发电机组故障预测方法

陈万志，李昊哲，刘恒嘉，王天元

（1.辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105；2.辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105；3.长春理工大学 计算机科学技术学院，吉林 长春 130022；4.国网辽宁省电力有限公司 营口供电公司，辽宁 营口 115000）

0 引言

风力发电机组的故障多源于发电机、齿轮箱、传动轴、叶片及变桨系统、偏航系统、电控系统等关键部件，可通过检测分析振动、应力、扭矩、温度、润滑油和电气等参数进行判别.风电场的SCADA（supervisory control and data acquisition）系统可实现对风电机组的监测监控功能.但基于SCADA数据的分析挖掘应用较少或仅用于人工统计，无法预测风电机组故障可能发生的情况[1-4].

由于对SCADA系统数据的分析已无法满足安全的需求，研究者们将SCADA系统数据与机器学习模型结合，对风电机组进行故障预测和诊断.文献[5]提出结合 ITD（intrinsic time-scale decomposition）和LS-SVM（least square-support vector machine）的风力发电机组轴承故障诊断方法.文献[7]提出一种基于粒子群优化 KFCM（kernel fuzzy c-means clustering）的风电齿轮箱故障诊断方法.文献[8]提出一种基于小波包变换BP（back propagation）神经网络的齿轮箱故障诊断方法.文献[9]提出一种基于小波包分析与 SVM 相结合的故障诊断新方法.文献[10]提出一种基于隐半 Markov模型的故障诊断和预测方法.目前利用SCADA数据进行分析挖掘还存在精准度不高、实时效果差等问题.

本文以某风场SCADA系统数据为基础，通过分析发电机温度、室外温度以及风速等参数，在SVM 模型的基础上融合 LSTM（long short-term memory）和SSA（sparrow search algorithm）优化SVM的方法实现风力发电机组短期故障预测.

1 整体框架

所提出风电机组故障预测模型的系统整体框架见图1.即通过同步风电机组SCADA系统小电机温度、液压温度、大电机3种温度、高速轴温度、齿轮油温度、风速以及室外温度等数据，并对其进行数据预处理，处理后的测试数据分别用于LSTM和SSA优化的SVM模型训练与测试；其次利用优化后的SVM对LSTM的短期预测数据进行分类判定，得到风电机组故障预测结果.最终实现基于SCADA实时和历史数据的风电机组未来短期故障的预测，为故障诊断与预测分析提供系统模型基础，为保障风电机组的安全可靠运行、适时运维保养和故障危害最小化提供科学依据.

图1 系统整体框架Fig.1 overall framework of system

2 系统模型

2.1 长短期记忆网络LSTM模型

LSTM网络是采用时间先后顺序开展反向误差传播算法进行网络训练的，适于处理时间序列变量的预测问题，而风电机组SCADA系统数据是与时间密切相关的，故LSTM模型适合风电机组数据的相关预测分析.

LSTM模型的输入为同步风电机组SCADA系统数据中9个关键数据字段的短期连续时间段内的实时和历史数据，输出是对应9个特征下一时间点的预期数据，见图2.

图2 LSTM模型的输入与输出Fig.2 input and output of LSTM

2.2 支持向量机SVM模型

SVM在解决二分类问题上具有良好的性能，适于LSTM模型的短期预测进行是否故障判别.

SVM模型的输入为同步风电机组SCADA系统数据中9个关键数据字段，将每种特征参数作为一个输入向量x，输入向量定义为

式中，An(n= 1,… ,9 )为特征参数的值.SCADA系统数据中风电机组运行状态有故障和正常两种.

C-SVM的约束式为

式中，ω，b为超平面定义的参数；l为SVM训练集数据中的帧数；iξ为松弛系数.

由于SCADA数据的特征参数非线性，故使用径向基函数RBF（radial basis function）作为内核函数K进行数据空间映射.K定义为

式中，γ为内核函数的预定义参数.

SCADA数据运行状态(x，y)的训练集从R9×R映射到Hilbert空间×R为

根据下式确定超平面(ω⋅xi) +b= 0 ，

式中，C为惩罚系数.

SVM模型由超平面的唯一解进行定义.其中

对于每条SCADA数据输入向量，由SVM模型预测判别结果输出为

SVM模型的分类过程原理见图3，其中N是支持向量ω的数量.

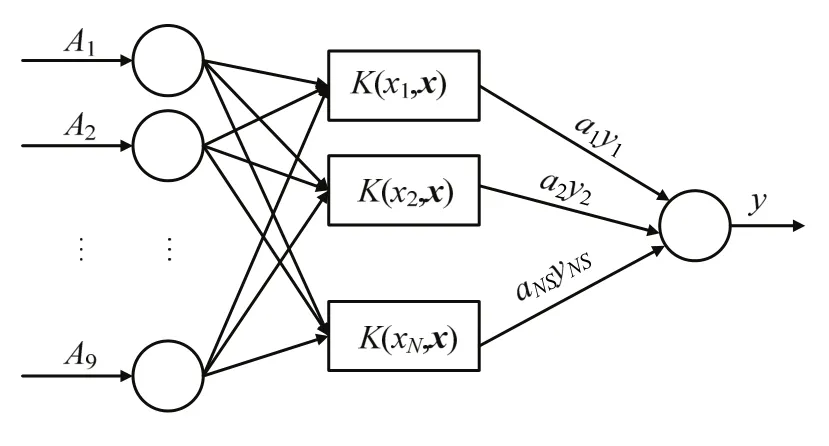
图3 SVM模型的输入与输出Fig.3 input and output of SVM

2.3 麻雀优化算法优化SVM模型

麻雀搜索算法SSA是一种源于麻雀觅食和反捕食行为的种群智能优化算法，具有寻优能力强、收敛速度快等优点，适合对SVM模型进行优化.

在模拟测试实验中，利用虚拟麻雀模拟寻找食物，由n只麻雀组成的种群为

式中，d为风电机组运行状态的因变量维数，d的值为9，表示9个特征参数.

所有麻雀的适应度值F表示为

在每次迭代过程中，发现者的位置更新为

式中，t为当前迭代次数；item-max为最大迭代次数；Xi,j为第i个麻雀在第j维中的位置；α为随机数；R2和ST分别为预警值和安全值；Q为服从正态分布的随机数；L为1×9矩阵，每个元素均为1.

在觅食过程中，一些加入者会监视寻找食物的发现者并去争夺更好的食物，加入者的位置为

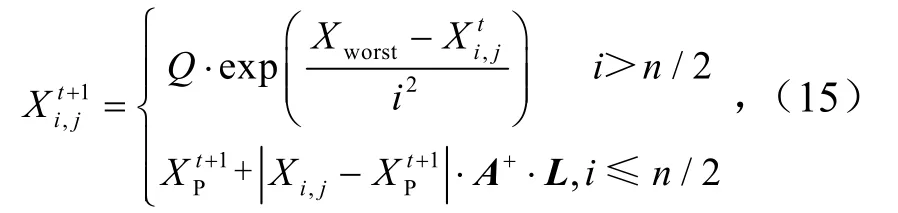
式中，XP和Xworst分别为最优位置和最差位置.A为一个 1×9的矩阵，元素随机赋值为 1或-1，且A+=AT(AAT)−1.

在模拟测试实验中，设意识到危险的麻雀占总量的10%至20%，这些麻雀的位置为

式中，Xbest为当前的全局最优位置；β为服从均值为0、方差为1的正态分布控制步长；K∈[-1,1]是一个随机数；fi为麻雀个体i的适应度值；fg和fw分别为当前全局最佳和最差的适应度值；ε为常数，避免分母为0.

2.4 风电机组SCADA系统数据特征分析

实验数据集为某风电场的 MADE型号风机的SCADA系统后台数据，其中基础数据包括风机型号、风机类型、记录时间等静态数据，以及通过传感器采集的温度、风速、功率等共计10个特征值，详细说明见表1.

首先对数据进行清洗及预处理，删除数据集中的异常样本，消除人为停机维护、调试等操作的主观影响，其次采用统计分析软件SPSS对特征进行主成分分析并得出特征权重，明确找出对因变量有影响的特征，进一步提高模型的准确度，具体分析结果见表2.

由特征重要性排序可知，液压温度、小电机温度及大电机温度特征权重较大，同时也是风机监测的重要指标，对于故障预测结果有着重要的影响，同时也从另一个侧面说明通过温度等参数预测风机故障状况是可行的，同时其他参数的特征权重也均在8%以上，因此选取这9个特征作为算法及模型的特征参数.

3 实验

3.1 实验环境

实验测试为云虚拟机模拟环境，硬件配置为Intel Xeon Gold 6266C@3.00GHz CPU，8.00GB内存，系统软件为64位Windows Server 2016 Standard操作系统，应用软件为Pycharm2020.1.

3.2 实验步骤

（1）采集数据并对数据进行预处理.

（2）利用历史数据训练 LSTM 模型，通过模型对未来短期数据进行预测，得到短期预测数据.

（3）利用历史数据训练SVM模型并使用SSA算法对SVM模型优化，得到的优化SVM模型能够判别风机运行状态.

（4）通过优化的SVM模型对LSTM得到的短期预测数据进行运行状态判别.

（5）将（4）中得到的运行状态与风力发电机组实际运行状态作比较，得到模型故障预测准确率.

3.3 数据采集和预处理

实验数据集为某风力发电场SCADA系统收集的历史后台运维数据，共包含电机温度、液压温度、齿轮油温度、高速轴温度、齿轮油温度、室外温度、风速和功率等10个维度，采样周期为30 s，为避免季节因素对实验的影响，选取某风机2018年7月、8月的SCADA数据共63 319条，手动删除异常值6 814条，其中包含停机维护、调试数据，以及不符合常理的无效数据.经处理后共计56 478条有效数据，将功率为正数的样本作为正常数据，将功率为0的样本标记为故障数据.

3.4 LSTM模型实验

分别对9个参数进行LSTM短期预测，再将其预测得到的值结合到一起，得到新的SCADA数据的短期预测数据.取10台运行的MADE型号风机各1 100条数据，共11 000条数据.划分数据集，各取前 1 000条 SCADA数据为训练集，剩下 100条SCADA数据为测试集.

首先采用训练集进行模型训练，并通过训练集后 50条数据预测一条新数据，其次把这条新的数据添加到训练集的末尾并另存为预测结果，再通过训练集新生成的后50条数据再预测一条新数据.重复进行100次，最终得到10台风机预测结果各100条，并与测试集中的实际数据作对比.图4和图5分别为1号风机大电机温度和液压温度预测值与实际值的对比.

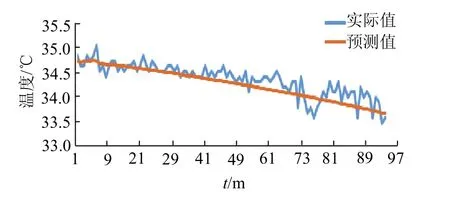
图5 液压温度预测值与实际值对比Fig.5 comparison between predicted and actual hydraulic temperature

3.5 SSA优化SVM实验结果

为测试经SSA改进后模型的性能和准确率，将其和未进行改进的 SVM 模型进行比较，分别使用SSA-SVM 和SVM 对相同数据集进行分类预测对比实验结果见图6和图7.SSA-SVM预测结果准确率为98.80%，SVM 预测结果准确率为 93.65%.经过 SSA改进的SVM模型的预测效果相比传统SVM效果有明显地提升.

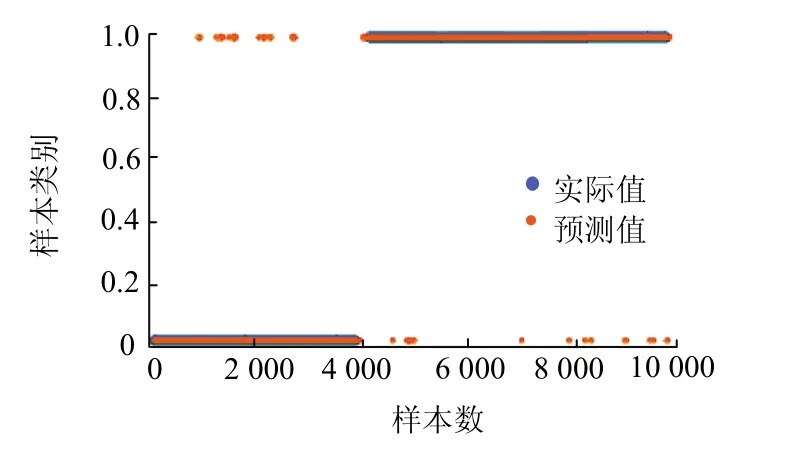
图6 SSA-SVM预测结果散点Fig.6 scatter plot of SSA-SVM prediction results

图7 SVM预测结果散点Fig.7 scatter plot of SVM prediction results

3.6 LSTM-SSA-SVM实验结果

LSTM短期预测得到10台MADE型号风机各100条新数据，使用优化的SVM对1 000条预测数据运行状态进行分类预测，并将分类预测得到的结果与该时间段的风电机组的实际运行状态作比较，预测正确的数据所占整体数据的百分比，即为LSTM-SSA-SVM模型预测风电机组故障的准确率.将1 000条预测数据加入训练好的SSA-SVM模型中进行测试，最终得到测试集准确率为97.90%，结果见图8.

图8 LSTM-SSA-SVM预测结果散点图Fig.8 scatter plot of LSTM-SSA-SVM prediction results

将本文模型与原始SVM模型和其他文献提出的风机故障预测模型作对比，对比结果见表3.

表3 模型预测准确率对比Tab.3 comparison of model prediction accuracy

通过对比可知，本文模型的准确率均略高于其他故障预测模型，证明其可行性和有效性，在一定程度上提升风电机组故障预测的精度.

4 结论

在传统 SVM 的基础上，提出一种 SSA优化SVM模型，结合LSTM预测风电机组短期数据对风电机组运行状态进行分类预测.现场数据测试实验结果表明，该融合模型预测准确率可达97.90%，相比其他故障预测方法精度更高.

当前所研究的风电机组故障来源仅是温度等特征对故障的影响，在后续的研究中，还应该将振动、器件老化等因素结合在一起进行分析，使风电机组的故障预测准确度更高.