梁端反对称静力加载模式下PC框架节点概率受力性能分析

宋鹏彦，王 晨，赵仰康，陈伟宏

（1.河北大学建筑工程学院，河北保定 071002；2.福州大学土木工程学院，福建福州 350108）

引言

结构施工过程中的材料加工工艺、人为误差、环境条件等因素均具有一定的不确定性，这些不确定性因素最终都会通过材料强度、弹性模量以及构件尺寸等结构参数的不确定性体现出来［1］。研究结构参数的不确定性对结构受力性能的影响以及结构参数的灵敏度分析，对结构的受力性能评估、功能函数的优化等问题具有十分重要的意义。

为研究结构参数不确定性对结构受力性能的影响规律，国内外一些学者做了相关的研究，并已经得到了一些成果。蒋亦庞等［2］考虑了9 个结构参数的不确定性，对砌体结构进行了地震易损性分析和灵敏度分析，结果表明结构参数不确定性对无筋砌体抗震性能的影响随着结构破坏程度的增大而增大；于晓辉等［3］研究了结构参数不确定性对RC 框架结构倒塌易损性分析的影响，结果表明：考虑结构参数不确定性时，结构的抗倒塌能力的对数标准差大了70%左右，其中结构参数中无约束混凝土峰值应变以及黏滞阻尼比的灵敏度最大。Choudhury 等［4］考虑了11个结构参数不确定性，分别对空腹框架结构、露天层框架结构和全填充框架结构进行了非线性动力分析和灵敏度分析。Celik 等［5］对RC 框架结构进行易损性分析时，考虑了钢筋强度、混凝土强度、结构阻尼、节点区粘结滑移系数、节点剪切强度以及节点剪切应变共6 个参数的不确定性，并分析了参数灵敏度；吴文朋等［6］在进行桥梁结构地震易损性分析时考虑了26 个不确定性参数，说明了在地震易损性分析时结构参数的不确定性和地震动的不确定性的影响都不容忽视。

此外，PC 框架结构由于二次浇注部位大多在梁柱节点处，所以梁柱节点处便成为了结构在受力过程中的薄弱部位［7-8］。基于上述背景，文中以PC 框架节点为研究对象，首先用PC 框架节点反对称低周反复加载试验验证OpenSEES 数值模型。在此基础上从材料本构和构件尺寸层面考虑12 个参数的不确定性，进行梁端反对称静力加载模式下PC 框架节点概率受力性能分析，研究结构响应参数的概率特征，分析轴压比对结构响应参数概率特征的影响，并且研究12个不确定性结构参数的灵敏度，将其影响程度大小进行排序。

1 PC框架节点数值模型的建立与验证

1.1 PC框架节点拟静力加载试验

文中以陈伟宏等［9］完成的PC 框架节点拟静力试验中的J1、J2 试件为分析对象，其中J1 试件柱端轴压比为0.17，J2 试件柱端轴压比为0.34，试件的几何尺寸和梁柱配筋图如图1所示，相关材料力学性能指标见表1。柱底端采用固定铰支座约束水平和竖直位移，柱顶端采用水平铰支座约束水平位移，加载方式为梁端反对称低周反复加载。

表1 试验材料力学性能指标实验值Table 1 Experimental values of mechanical property indexes of component materials

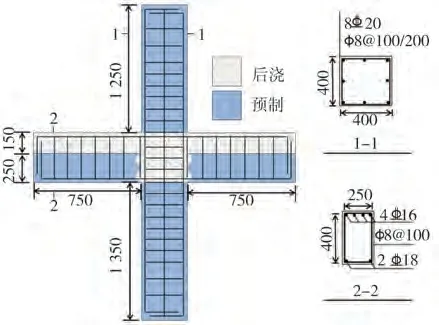
图1 PC 框架节点试件构造配筋详图（单位：mm）Fig.1 PC frame joint member reinforcement drawing（Unit：mm）

1.2 建模方法

文中利用OpenSEES 平台建立与试验1：1 的PC 框架节点数值分析模型。试验构件属于湿式连接PC 框架结构，工程上湿式连接PC 框架结构一般以达到现浇结构的性能为目标，所以其建模方法也应与现浇结构类似。湿式连接PC 框架节点核心区由于采用了先浇-后浇的施工工艺，节点区的剪切行为和黏结滑移效应不能忽略［10］。文中PC框架节点核心区采用BeamColumJoint单元（图2）模拟，梁、柱构件采用基于柔度法的非线性梁柱单元（图3）模拟。现将数值模型中使用到的单元模型和材料本构模型详细介绍如下。

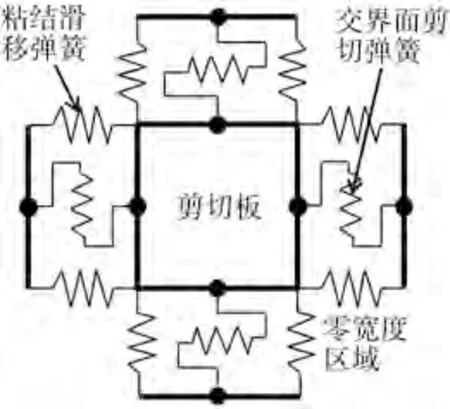
图2 BeamColumJoint单元Fig.2 BeamColumJoint element model

图3 梁、柱单元模型Fig.3 Beam and colum element model

1.2.1 单元模型

（1）非线性纤维梁柱单元：文中采用基于柔度法非线性梁柱单元模拟梁、柱构件，该单元采用力插值型函数，沿单元长度进行Gauss-Lobatto 数值积分，从而描述单元的内力分布情况。该单元描述截面的受力行为采用纤维截面模型，并且可以通过给纤维截面赋予不同的本构关系来考虑箍筋对混凝土的约束作用，并且可对梁、柱分别采用Corotational 和PDelta 方法描述结构的几何非线性行为。

（2）BeamColumJoint 单元：与现浇整体节点相比，PC 框架节点由于采用预制和后浇的施工工艺，存在着节点核心区浇筑不密实和灌浆不充足等问题，节点核心区剪切行为明显、钢筋粘结滑移效应会引起结构强度和刚度退化。根据上述特点，各国学者对PC 框架节点核心区受力机理进行深入研究后，提出了多种框架节点数值分析模型，如转动铰模型、Joint2D 模型［10］、BeamColumJoint 模型［11］等。其中BeamColumjoint 模型已被集成于OpenSEES 之中，该模型由剪切板单元和零长度弹簧单元组成，描述节点核心区受力破坏特征的机理为：1个剪切板单元用来模拟与节点核心区剪切破坏相关的强度和刚度损失，8个零长度的粘结滑移弹簧单元用来模拟嵌入节点核心区的梁和柱纵向钢筋粘结强度的退化，4 个零长度的剪切弹簧用来模拟节点与梁、柱接触面上抗剪能力传递的损失。

1.2.2 材料模型

（1）混凝土本构模型：采用Concrete02 本构模型（图4）。其中箍筋对核心区混凝土的约束作用通过强度提高系数K来反映，混凝土强度提高系数K与混凝土强度、配箍率以及箍筋屈服强度有关。本构模型中的残余强度取峰值强度的20%，混凝土抗拉强度取抗压强度的10%。

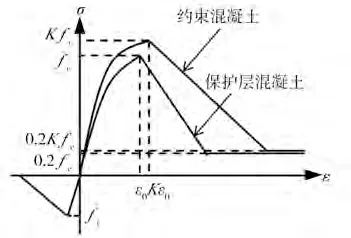
图4 混凝土材料模型图Fig.4 Concrete materials constitutive model

（2）钢筋本构模型：采用Steel02 模型（图5）。该模型是由斜率为E0的初始渐近线和斜率为E1的屈服渐近线组成，并且可以反映材料的包辛格效应。文中钢筋强度参数取试验值，形状参数R0=18.5，CR1=0.925，CR2=0.15。

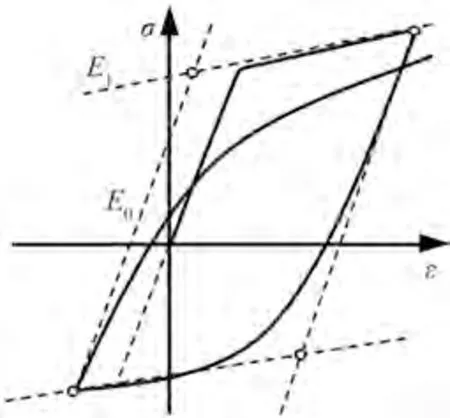
图5 钢筋材料本构模型Fig.5 Steel materials constitutive mode

（3）剪切板弹簧：采用Pinching4模型（图6）。该本构模型单调加载的骨架曲线需要定义8个点共16个参数，文中根据吴健秋的建议，采用修正斜压场理论（MCFT）来定参，计算构件节点核心区在单调加载下的剪应力-剪应变关系曲线，识别曲线该16 个参数，如图7 所示（负向与正向曲线关于原点对称）。在模拟循环反复荷载作用时，Pingching4 本构模型还需定义描述卸载-再加载路径的6 个参数，以及描述强度和刚度退化的12个参数，文中参照文献［12］选取。

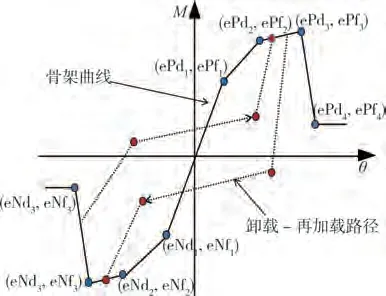
图6 Pinching 4材料本构模型Fig.6 Pinching 4 materials constitutive model

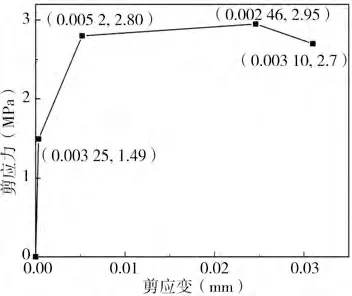
图7 Pinching 4模型关键点选取Fig.7 Pinching 4 materials key point selection

（4）粘结滑移弹簧：单元中的粘结滑移弹簧采用钢筋滑移模型Bar-Slip 模拟，该模型可以综合考虑混凝土特性、钢筋特性、锚固长度以及构件截面尺寸等对钢筋滑移的影响。

（5）剪切弹簧：在一般情况下，加载过程中梁、柱与节点交界面处只会出现相对转动而不会出现垂直的滑动，接触面处的抗剪刚度都很大，一般处于弹性工作状态，所以文中将零长度交界面剪切弹簧简化为大刚度的弹性材料［13］。

1.3 数值模型的试验验证

建立J1 试件和J2 试件的反对称低周反复加载数值模型，得到试件的滞回曲线，如图8 所示。提取骨架曲线，与试验结果对比如图9 所示，模拟结果与试验结果有一定差异，原因可能是数值分析中材料本构或节点单元模型受力特征与真实情况有出入。但两者曲线走势和相应数值点大体相近，能很好的模拟捏拢现象，能够用该数值模型模拟PC框架节点的受力性能。

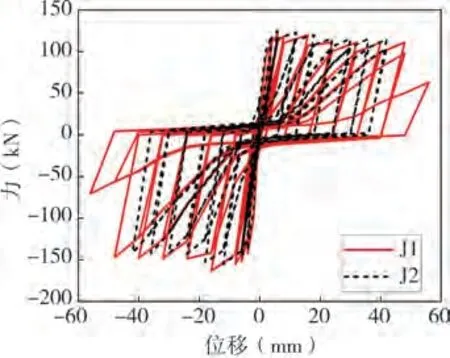
图8 滞回曲线模拟结果Fig.8 Hysteresis loops numerical results

图9 骨架曲线对比Fig.9 Skeleton curve comparison results

2 考虑结构参数不确定性的PC框架节点概率受力性能分析

2.1 基本随机变量的选取

文中考虑混凝土抗压强度fc、混凝土抗拉强度ft、纵筋屈服强度fy、纵筋弹性模量Es、箍筋屈服强度fyv、混凝土保护层厚度Cc、梁截面高度H1、梁截面宽度B1、梁总长度L1、柱截面宽度B2、纵筋直径D和箍筋间距s共计12 个参数的不确定性，其中相关材料参数概率分布特征按文献［14］确定，结构尺寸参数概率分布特征按文献［15］确定。各参数概率统计特征列于表2。文中简化了分析方法，不考虑参数之间的相关性，认为结构参数是相互独立的。

表2 结构参数概率特征Table 2 Probabilistic characteristics of structural parameters

2.2 结构的概率受力性能分析

拉丁超立方抽样（LHS）是一种分层抽样方法，相比于其他抽样方法，拉丁超立方抽样（LHS）具有精度高、效率高的优点。根据上述随机变量的概率特征，故文中采用拉丁超立方抽样方法（LHS）得到500组结构参数随机样本点。

在PC框架节点OpenSEES 数值模型和500组随机样本点的基础上，进行PC 框架节点的概率受力性能分析。控制柱顶端轴压比为0.2，加载方式采用梁端反对称静力加载，采用位移控制加载模式，具体加载示意图如图10 所示。将500 组结构参数随机样本点依次输入结构数值模型中，以梁左端受力变形为参考点，得到500 组样本点的剪力-位移关系曲线（图11）。由图11 可知：结构参数的不确定性使结构的响应也具有了不确定性。

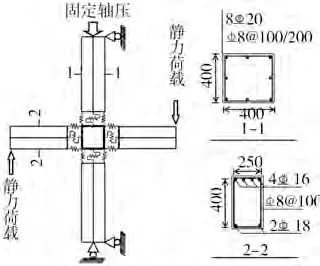
图10 梁端反对称静力加载模型（单位：mm）Fig.10 Anti-symmetric loading model at beam end（Unit：mm）

图11 500组样本的力-位移关系图Fig.11 Force-displacement relationship plot for 500 samples

根据500 组PC 框架节点受力数值分析结果，对结构响应参数进行概率统计分析。文中选用峰值剪力Vp、峰值位移Δp、屈服剪力Vy和屈服位移Δy为结构的响应参数。其中，结构受力屈服点采用等效能量法确定，原理如图12 所示，图中，其中为边弯曲的三角形面积，为梯形的面积，D点为等效屈服点。

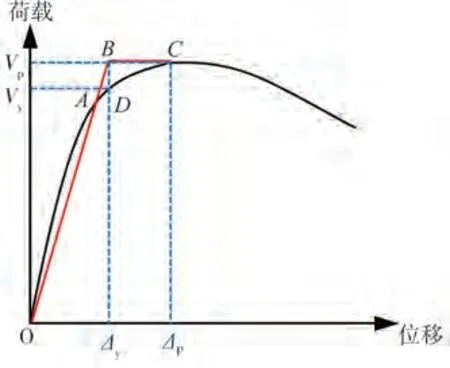
图12 等效能量法确定屈服点Fig.12 Equivalent energy method to determine the yield point

梁端反对称静力加载模式下PC 框架节点结构的最大剪力Vp、峰值位移Δp、屈服剪力Vy、屈服位移Δy的概率特征值、偏度系数和峰度系数列于表3，分析可知：各响应参数均表现出离散性，且与正态分布相比均具有一定的偏态，均为左偏分布。采用核密度（KDE）估计4个响应参数的概率密度函数，与相应的对数正态密度函数比较，图13～图16 给出了Vp、Δp、Vy和Δy的参数分布直方图、KDE 估计概率密度函数曲线以及相应的对数正态分布概率密度函数曲线，由图可知：KDE 估计得到的概率密度函数曲线与对数正态分布的概率密度函数曲线相似，结构的4个响应参数的离散特征大致可用对数正态分布进行描述。

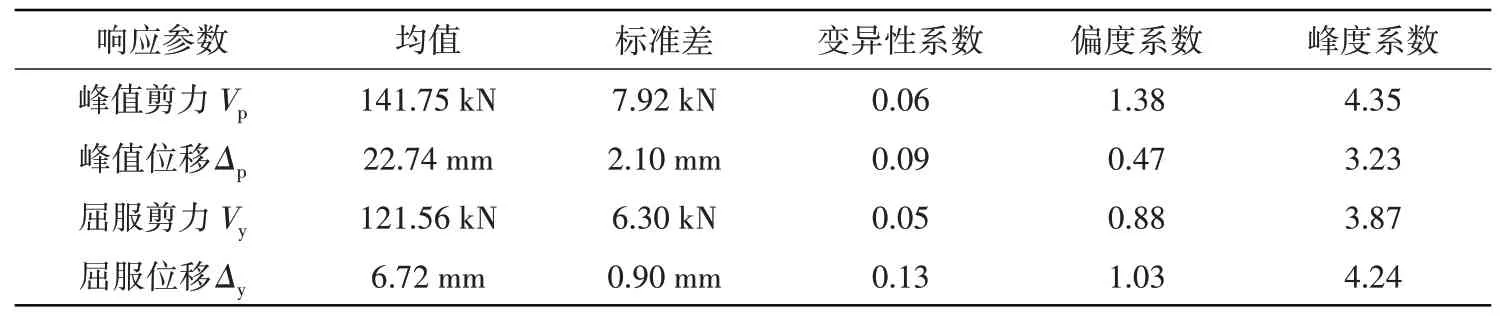
表3 结构响应参数概率特征统计Table 3 Probabilistic characteristic statistics of structural response parameters

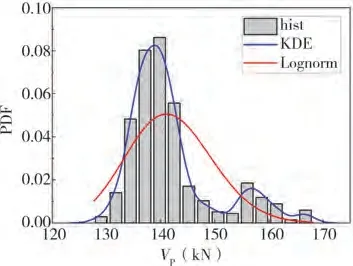
图13 峰值剪力Vp概率统计Fig.13 Probability statistics of the peak shear force Vp

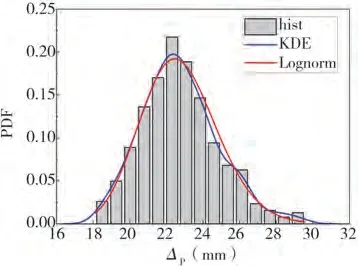
图14 峰值位移Δp概率统计Fig.14 Probability statistics of the peak displacement Δp

图15 屈服剪力Vy概率统计Fig.15 Probability statistics of yield shear force Vy

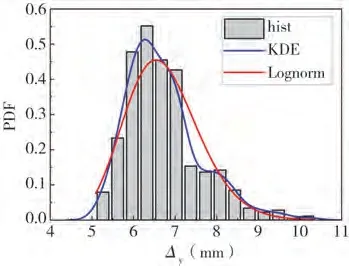
图16 屈服位移Δy概率统计Fig.16 Probability statistics of yield displacement Δy

2.3 轴压比对结构概率受力性能的影响

在上述研究的基础上，通过分析不同的轴压比作用下结构响应参数概率特征值的变化情况，进一步研究轴压比对该结构模型响应参数概率特征的影响。具体分析步骤为：在柱顶端分别设置不同的轴压比（0.1～1.0），得到相应的500 组荷载-位移曲线，分别统计最大剪力Vp、峰值位移Δp、屈服剪力Vy和屈服位移Δy的概率特征，列于表4。分析可知：在轴压比为0.1～0.7时，峰值剪力、峰值位移、屈服剪力和屈服位移的变异性系数分别在0.053 3～0.057 2 之间、0.089 5～0.092 6 之间、0.049 2～0.052 7 之间和0.129 4～0.141 1 之间，当轴压比为0.8～1.0时，峰值剪力、峰值位移、屈服剪力和屈服位移的变异性系数分别在0.057 9～0.059 7之间、0.092 2～0.097 7之间、0.053 7～0.055 0 之间和0.149 1～0.142 5之间。可见轴压比达到0.8 及以上时，结构响应的离散性有增大的趋势。分析表明，采用BeamColumJoint单元虽然能很好地反应PC框架节点的受力性能，但轴压比的变化对其构件响应的影响并不敏感。

表4 不同轴压比下结构响应概率特征统计Table 4 Probabilistic characteristics of structural response under different axial pressure ratios

2.4 不确定性参数的灵敏度分析

为进一步研究上述12 个结构参数对结构响应影响程度的大小，以轴压比为0.2 的梁端反对称静力加载数值模型为基础，对结构参数进行灵敏度分析，具体步骤如下：

（1）以全部结构参数取离散值的样本为数值模型的输入，统计结构响应参数的标准差s。

（2）每次只对1个结构参数取均值，其余结构参数取离散值，分别统计12组样本对应的结构响应参数的标准差σi（i=1～12）。

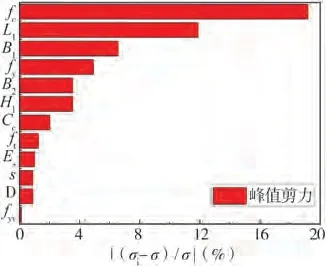
图17 Vp的标准差相对变化率Fig.17 Relative rate of change of the standard deviation of the Vp

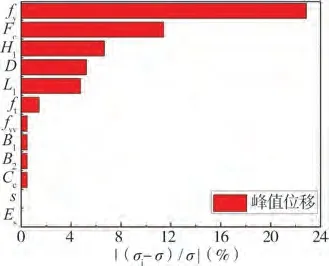
图18 Δp的标准差相对变化率Fig.18 Relative rate of change of thestandard deviation of the Δp

图19 Vy的标准差相对变化率Fig.19 Relative rate of change of the standard deviation of the Vy

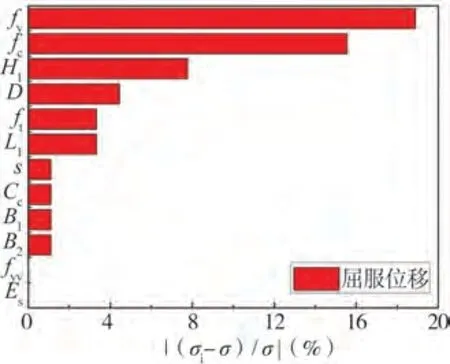
图20 Δy的标准差相对变化率Fig.20 Relative rate of change of the standard deviation of the Vy

由图可知，对于峰值剪力Vp和屈服剪力Vy，灵敏度最大的结构参数为混凝土抗压强度fc和梁长L1；对于峰值位移Δp和屈服位移Δy，灵敏度最大的结构参数为纵筋屈服强度fy和混凝土抗压强度fc。需要说明的是，本文梁端反对称静力加载数值模型中的反对称荷载施加位置为梁的端部，由于文中选取了梁长度为不确定性参数，因此梁长度参数不确定性的影响可以理解为加载点位置不确定性的影响。箍筋屈服强度fyv、纵筋弹性模量Es、箍筋间距s以及保护层厚度Cc等结构参数的灵敏度较小，在结构受力性能分析时可忽略其不确定性所产生的影响。

3 结论

文中基于OpenSEES 平台建立了PC 框架梁柱节点数值模型，在此基础上考虑了12 个结构参数不确定性，在梁端反对称静力加载模式下，进行了概率受力性能分析，统计了响应参数的概率特征，研究了轴压比对随机受力性能呢的影响，并分析了结构不确定性参数的灵敏度大小，得出的结论如下：

（1）结构参数的不确定性会导致结构响应的不确定性，结构响应的离散特征可用对数正态分布描述。

（2）在梁端反对称静力加载模式下，柱端轴压比超过0.8时，结构响应的离散性有增大的趋势。

（3）灵敏度分析表明，PC框架节点在梁端反对称静力加载模式下，对峰值荷载和屈服荷载影响较大的是混凝土抗压强度和梁长，对峰值位移和屈服位移影响较大的是纵筋屈服强度和混凝土抗压强度。而箍筋屈服强度、纵筋弹性模量、箍筋间距以及保护层厚度等结构参数的灵敏度较小，在结构随机受力性能分析时可忽略其不确定性产生的影响。