基于主成分分析方法的变电工程造价关键影响因素识别
李凌云,席小娟,李旭阳,卫 璞,康艳芳
(国网河南省电力公司经济技术研究院,河南 郑州 450052)
电网工程是事关国计民生和国家安全的重要基础设施,是经济发展的命脉和动力,变电站是其中的重要组成部分。变电站是电网公司的重要资产,对变电工程造价的精准控制有利于提高公司变电工程建设投资效率,提高公司精益化管理水平[1-2]。变电工程造价的费用构成共分为4个部分,即建筑工程费、设备购置费、安装工程费和其他费用。影响变电工程造价的因素大致可分为宏观因素和微观因素,宏观因素包括政府政策因素、社会经济整体发展水平、电网技术发展水平、设备材料市场变化因素等,微观因素包括设计人员专业技术能力、工程站址条件、负荷发展水平、工程地质水文条件等[3-4]。这些因素繁多且关系复杂,对变电工程造价的影响存在不确定性。如何合理控制变电工程造价,助力电网公司精准投资成为迫切需要解决的问题。
目前,国内针对变电工程造价的影响因素研究多集中于定性分析或者少数样本的定量分析[5-6],基于大量历史工程数据的分析比较少。本文基于某省2019—2021年的变电工程造价决算数据,采用主成分分析方法研究影响变电工程造价的各类因素之间的内在联系,从诸多因素中识别出影响变电工程造价最为关键的因素,为电网公司精准控制变电工程造价提供借鉴和参考,助力电网公司高质量发展。
1 主成分分析方法
主成分分析(principal component analysis,PCA)是一种常用的多元统计方法,主要用于研究多个变量之间的相关性,即利用少数若干主成分来表示多个变量之间的关系。具体方法是对原始变量进行分析,归纳出少数若干主成分,以保证归纳出的主成分能够反映原始变量的关系[7-8]。主成分分析方法的特点是,将原始变量包含的复杂信息总结归纳为少数若干主成分包含的简单信息,将问题变得简单化,但是数据依然是科学有效的。
主成分分析法主要包括以下步骤。
1)对原始数据进行标准化处理

(1)

相应地,将变量作标准化处理,得到如下标准化指标变量
(2)
2)计算相关系数矩阵R
R=(rij)m×m
(3)
(4)
式中:rii=1,rij=rji,rij是相关系数,表示第i个指标和第j指标之间的关系。
3)计算相关系数矩阵的特征值与特征向量
对特征方程|λI-R|=0求解,计算得到特征值λi(i=1,2,…,m),λ1≥λ2≥…≥λm≥0;再计算特征值λi的特征向量ui(i=1,2,…,m),其中uj=(u1j,u2j,…,umj)T,特征向量组成m个新指标变量为
(5)
式中:y1为第1主成分,y2为第2主成分,ym为第m主成分。
4)选择p(p≤m)个主成分,计算综合评价值
计算特征值λj(j=1,2,…,m)的信息贡献率和累积贡献率,用bj表示主成分ym的信息贡献率,得到
(6)
用ap表示主成分y1,y2,…,yp的累积贡献率,则有
(7)
若ap接近1(一般ap的范围为85%~95%)时,则用前p个指标变量y1,y2,…,yp作为p个主成分,代替原来m个指标变量,再对p个主成分进行综合分析。
5)计算综合得分
用bj表示第j个主成分的信息贡献率,则有
(8)
根据综合得分值评价构成造价的主成分。
2 基于PCA的变电工程造价关键影响因素识别
2.1 变电工程造价影响因素梳理
影响变电工程造价的因素错综复杂,首先需要识别出常见的影响因素。本文基于某省2019—2021年的电网工程造价数据,经过初步梳理得到24个变电工程造价影响因素,分别为额定电压、智能变电站、变电站型式、本期主变台数、主变容量、主变单价、本期高压侧出线回数、本期低压侧出线回数、高压侧配电型式、高压侧断路器台数、高压侧断路器单价、低压侧配电型式、低压侧断路器台数、低压侧断路器单价、低压电容器数量、低压电容器单价、二次设备单价、智能化相关设备单价、场地平整费用、地基处理费用、进站道路费用、海拔、地形地貌、污秽等级。
2.2 基于PCA的变电工程造价关键影响因素筛选
在对变电工程造价影响因素初步梳理后,发现并不是所有的指标都对变电工程造价产生了明显影响,有一部分指标在特定范围内的波动只会对工程造价产生很小的影响,所以需要通过SPSS软件进行主成分分析,对过去3年的指标数据集进行处理,从众多因素中识别出对变电工程造价影响最为显著的关键影响因素。
2.2.1 计算影响因素的相关矩阵
首先对2019—2021年的样本数据做标准化处理,然后利用SPSS软件对样本数据开展主成分分析,通过计算各影响因素之间的相关系数,得到各个影响因素之间的关联程度。各影响因素的相关矩阵如表1所示。

表1 变电工程造价影响因素主成分分析相关矩阵(部分)
若两个因素的相关系数越接近1,则这两个因素的相关性越强。从表1可以看出,存在许多相关因素相关性较强的现象,说明样本数据存在信息重叠。需要消除多重共线性、降维处理,才能适用于主成分分析法。
2.2.2 计算解释的总方差
通过计算得到各个主成分对应的特征值,把特征值按照由大到小的顺序重新排序,得到碎石图,如图1所示。如果特征值小于1,则证明基本变量的影响力度大于该主成分因素,应当删除该主成分因素,提取特征值大于1的主成分。

图1 变电工程造价影响因素主成分分析碎石图
从图1可以清晰地看出提取主成分的信息解释情况,可从2019—2021年变电工程造价影响因素集中提取7个特征值大于1的因素。
采用方差最大化的正交旋转方法,得到解释的总方差,如表2所示。
从表2中可知,前7个主成分的累计方差达到了71.957%,能够解释变电工程造价影响因素的大部分信息。
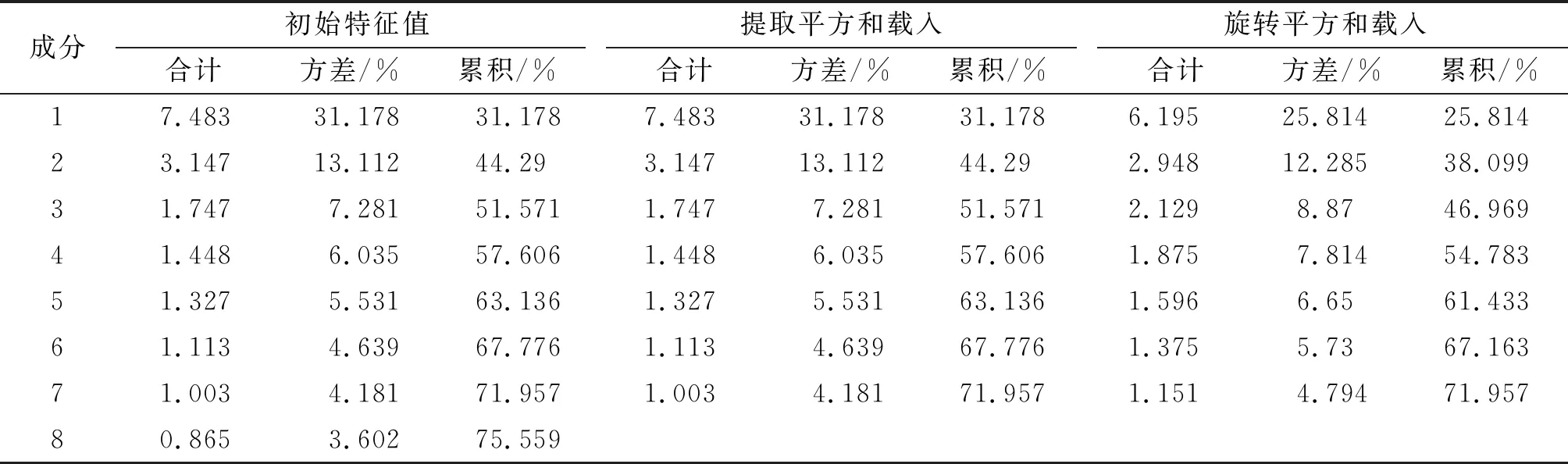
表2 变电工程造价影响主成分分析解释的总方差
2.2.3 关键因素筛选
通过碎石图和解释的总方差,得到了7个主成分,其中所包含的信息量能够代表近3年变电工程造价的影响因素。进一步通过SPSS软件得到旋转成分矩阵,如表3所示。成分旋转矩阵中的值即为各变量与各主成分间的相关系数,对前7个主成分与每个变量的相关系数进行比较,可以选出相关系数较大的主要变量,即得到变电工程造价关键影响因素。

表3 变电工程造价影响主成分分析旋转成分矩阵

表3(续)
从表3中可以看出,第1列中,主变容量系数最大,说明第一主成分是主变容量;第2列中,高压侧配电型式系数最大,说明第二主成分是高压侧配电型式,依次类推,得到第三主成分是本期高压侧出线回数,第四主成分是低压电容器数量,第五主成分是智能变电站,第六主成分是二次设备单价,第七主成分是污秽等级。
综上所述,通过主成分分析法最终筛选出的变电工程造价关键影响因素是:主变容量、高压侧配电型式、本期高压侧出线回数、低压电容器数量、智能变电站、二次设备单价、污秽等级。
3 变电工程造价关键影响因素验证
采用多元线性回归法来验证上述7个影响因素是否是近3年来变电工程造价的主要影响因素。以主成分分析得到的7个关键影响因素为自变量,以变电工程造价为因变量做回归分析,得到回归分析结果如表4至表6所示。

表4 变电工程多元线性回归分析的拟合度

表5 变电工程多元线性回归分析的显著性检验效果

表6 变电工程多元线性回归方程系数
从表4可以看出,调整后的R2为0.956,说明经过主成分分析得出的7个关键影响因素可以解释95.6%的近3年变电工程造价水平,拟合度较高。同时,从表5可以看出,多元回归模型结果显著,即近3年变电工程造价与主变容量、高压侧配电型式、本期高压侧出线回数、低压电容器数量、智能变电站、二次设备单价、污秽等级等指标之间存在显著关系。
多元线性回归方程系数显示了各影响因素对变电工程造价的显著性,Sig.值越小,说明该影响因素对造价的影响越大。由表6可知,对于近3年变电工程造价,主变容量、高压侧配电型式、电容器数量、二次设备单价、本期高压侧出线回数的显著性(Sig.值)明显很小,非常接近零,说明这5个因素对变电工程造价存在着显著影响。而是否为智能变电站及污秽等级的Sig.值均大于0.3,在置信水平下可以认为这2个因素对变电工程造价的影响并不显著,因此不将其作为关键影响因素进行考虑。
根据多元线性回归分析,进一步筛选出了变电站工程造价的5个关键影响因素,即主变容量、高压侧配电型式、本期高压侧出线回数、低压电容器数量、二次设备单价。
4 结语
本文基于某省近3年大量的变电工程决算数据,利用主成分分析和多元回归分析得到变电工程造价5个关键影响因素,即主变容量、高压侧配电型式、本期高压侧出线回数、低压电容器数量、二次设备单价。管理人员应重点关注这些关键影响因素,在前期阶段尽可能地充分论证此类参数,以期合理控制变电工程造价,实现精准投资。

