新型箝位式压电电机的设计研究

岳志涵，潘巧生，陶圣至，商静怡，李晓杰

(合肥工业大学仪器科学与光电工程学院测量理论与精密仪器安徽省重点实验室，安徽合肥230009)

1 引 言

近年来随着航空航天、生物医疗、电子信息、精密仪器等高新科技领域的发展以及现代工业对高精度自动化控制的需求越来越大，传统的电磁电机由于原理和结构的限制已经不能满足诸多领域的需求，由此诞生出新型电机，压电电机是其中较为成熟的一种。压电电机具有诸多优势，如可以在真空低温等极端环境工作，无电磁和噪声干扰[1，2]，位移分辨率高，动态响应快，控制性能好，结构简单设计灵活[3，4]，可实现精密运动控制[5，6]等，受到现代工业、高新科技领域的青睐，并且被广泛应用于航天器、机器人、照相机以及医疗设备等领域[7，8]。传统压电电机普遍以锯齿波作为激励信号，但在每个步进周期中动子会有回退现象，无法保证定向运动，进而诞生了同步箝位式压电电机。同步箝位控制原理结合了压电超声马达的谐振驱动和尺蠖马达的控制机理两个特点，克服了两者的缺点：压电超声马达工作过程中存在滑动摩擦和尺蠖马达准静态工作频率较低[9～15]。同步箝位式压电电机采用方波作为激励信号，保证方波形式的位移运动，优势在于能在驱动部分运动速度为零处卡紧和松开，理论上无滑动摩擦存在，效率较高，损耗减少。例如贺良国等研究的新型同步箝位控制压电马达，该马达总效率可达18.5%[16],但此类箝位式马达受到方波作为激励信号的限制，当工作频率接近箝位结构的共振频率时，位移波形会出现趋向于正弦波的失真情况，无法于谐振态工作。为此，本团队前期提出多级音叉结构，通过周期性机械振动波形合成产生机械方波[17]，这种思路能够提高箝位部分的振幅与频率，但结构过于复杂，设计难度极高。为降低箝位结构的复杂度，有学者对降低马达振子精度做过研究，但效果并不理想[18]。本次设计箝位部分不再采用方波而是直接采用正弦波做激励信号，由于在实际情况中滑台的存在会对箝位部分正弦波形式的位移运动进行修正，实验结果表明正弦波同样能达到方波的效果，且以正弦波作为激励不会受到箝位部分共振频率的干扰，电机的工作频率可再度提升，性能亦得到改善。

根据上述分析，本文设计结构具有以下优势：

(1) 降低结构设计难度，简化箝位部分结构。相较于传统箝位式压电电机，无需通过波形合成产生机械方波；同时与超声电机相比简化了复杂的模态简并设计流程。

(2) 可以于准静态和谐振态下工作，准静态下实现低速高精度，谐振态下实现高速大步距。

2 结构及工作原理

图1所示装置为本团队设计的新型箝位式压电电机，可根据功能区分为驱动部分和箝位部分。

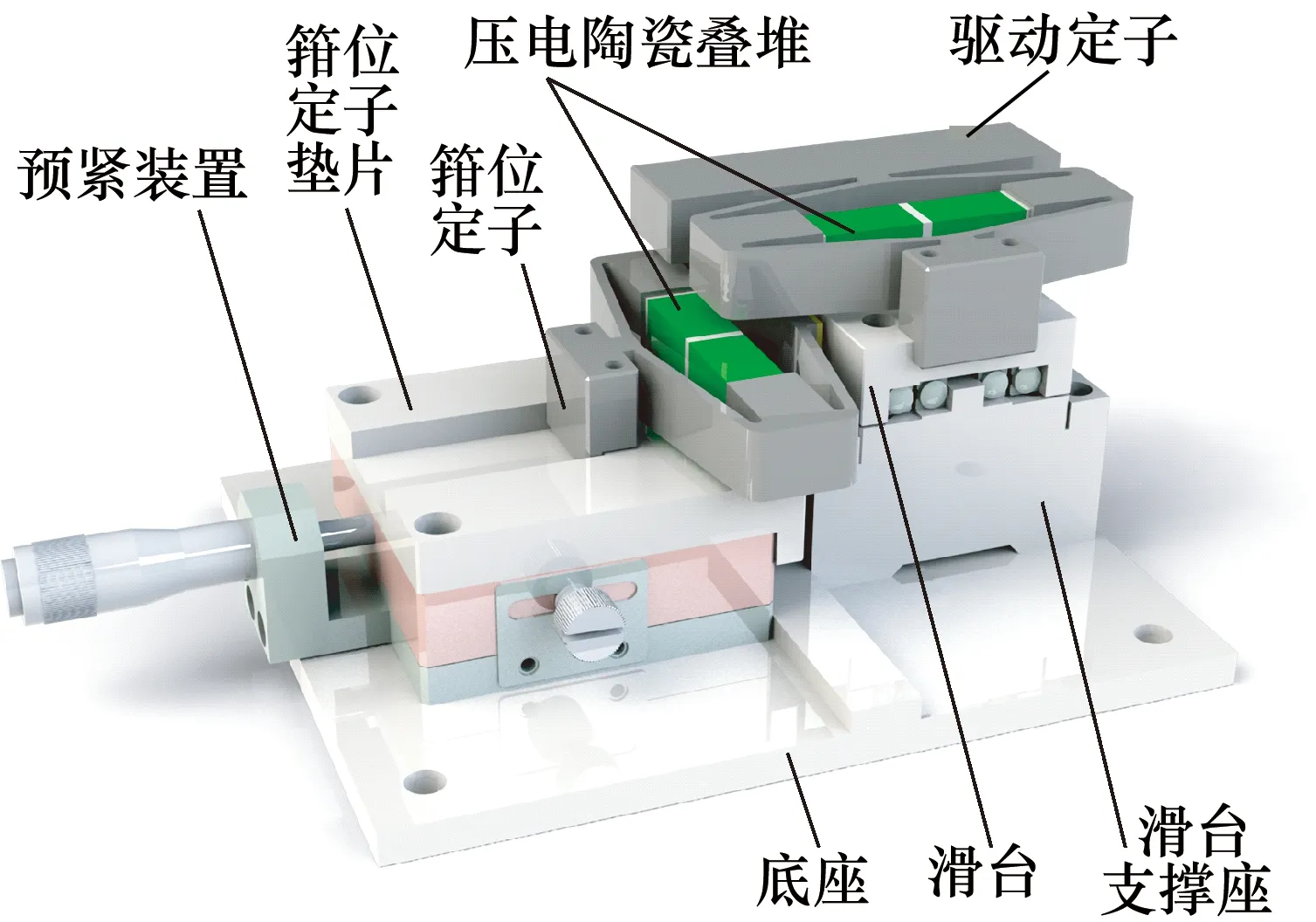
图1 新型箝位式压电电机Fig.1 A novel piezoelectric drive motor using the way of clamping mechanism

2.1 结构组成

驱动部分为图1中右半部分，该部分由驱动定子来驱动滑台上端盖的移动，滑台支撑座将滑台抬升至与箝位部分同一高度，驱动定子与滑台上端盖、滑台下端盖与滑台支撑座均采用螺栓加定位面定位方式固定，滑台支撑座通过螺栓与左侧面定位固定在底座上。

箝位部分为图1中左半部分，该部分通过箝位定子的伸缩来实现对滑台上端盖的卡紧与分离，垫片将箝位定子抬升至相应高度，选用氧化铝陶瓷片贴于接触表面减少磨损。预紧装置利用微分筒来调节箝位定子与滑台上端盖的初始间距,优化箝位部分的正弦波振型，保证压电马达箝位性能的正常发挥。

2.2 工作原理

该装置理想状况下于1个工作周期内可分为步进与箝位2个连续的工作状态。如图2，标红部分为步进过程各部分位移曲线与模型，此过程发生在0到 π/ω时间段内(ω为运动角频率)，箝位开关做图中正弦波形式位移运动，但不触碰滑台，滑台自由移动；标蓝部分为箝位过程，此过程发生在 π/ω到2 π/ω时间段内，箝位开关受到滑台的限制从而使波形被修正为方波形式，如图中箝位开关实际运动曲线，此时驱动部分有后退趋势(默认步进过程为前进)，但箝位开关卡紧使得滑台无法后退(实际每个周期都会有微量后退)，保证了滑台的定向移动。

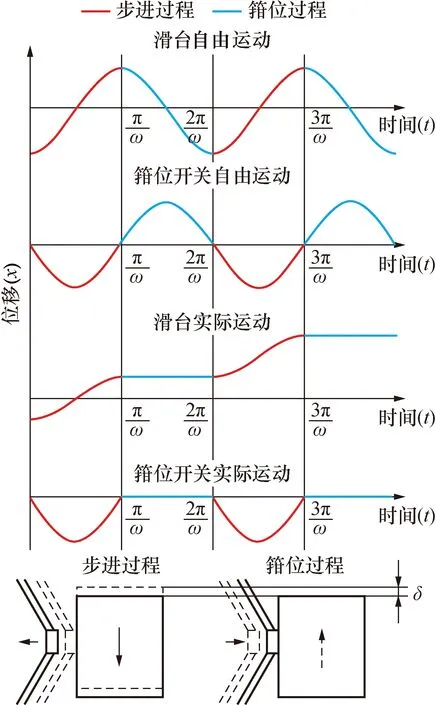
图2 压电电机工作过程Fig.2 Piezoelectric motor working process

能够实现步进运动需要具备驱动过程和箝位过程，并且两者要有一定的时序关系即两者激励信号有一定的相位差，相位差的超前与滞后影响滑台的前进与后退。

根据步进位移图像，该压电电机在工作时：

(1) 空载运动时，箝位开关在0到 π/ω的时间段内处于松开状态(实际是以正弦波位移形式运动，但未触碰到滑台侧面)，此时驱动部分可向前产生位移；若箝位开关在 π/ω到2 π/ω时间段内处于松开状态，而0到 π/ω的时间段内处于夹紧状态，则驱动部分可反向产生位移。

(2) 通过微分筒调节滑台与箝位开关的初始间距，保证开关在驱动部分速度为零时及时卡紧与松开，可有效避免冲击与滑动摩擦，保证电机的正常运行。

3 结构设计与仿真

为了设计恰当的驱动部分与箝位部分谐振频率以及验证结构的可行性，利用有限元仿真软件ANSYS对驱动部分和箝位部分进行仿真，在SOLIDWORKS中设计定子末端质量块尺寸保证驱动部分与箝位部分谐振频率一致，设计的成品模型各部分参数如表1所示。

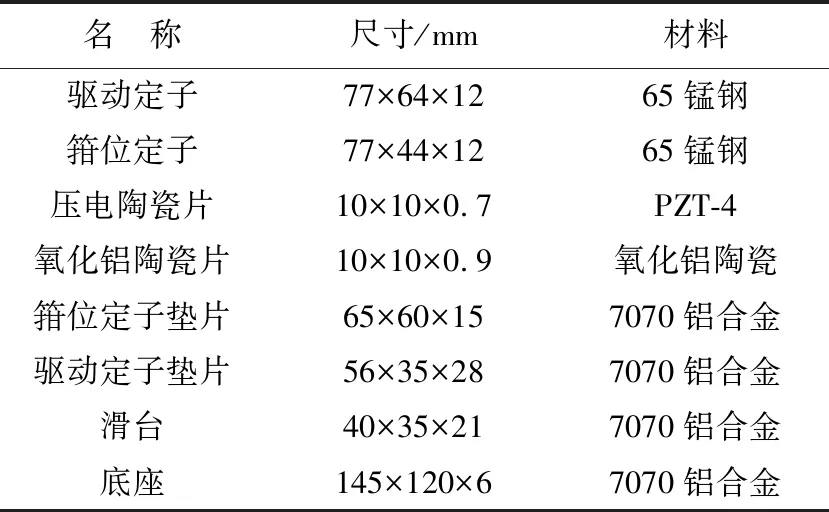
表1 主要结构参数Tab.1 Main structure parameters

3.1 驱动部分模态分析

图3为驱动部分的谐振模态仿真结果，滑台上端盖采用7070铝合金，驱动定子采用65锰钢，压电叠堆采用PZT-4。该仿真模型的六阶谐振频率为571 Hz。

图3 驱动部分六阶谐振模态ANSYS仿真Fig.3 ANSYS simulation of the sixth resonant mode of the driving part

此阶谐振频率做图4形式的振动方式，能量可沿所需方向集中释放，实际测量该模型此阶谐振频率约在540 Hz。

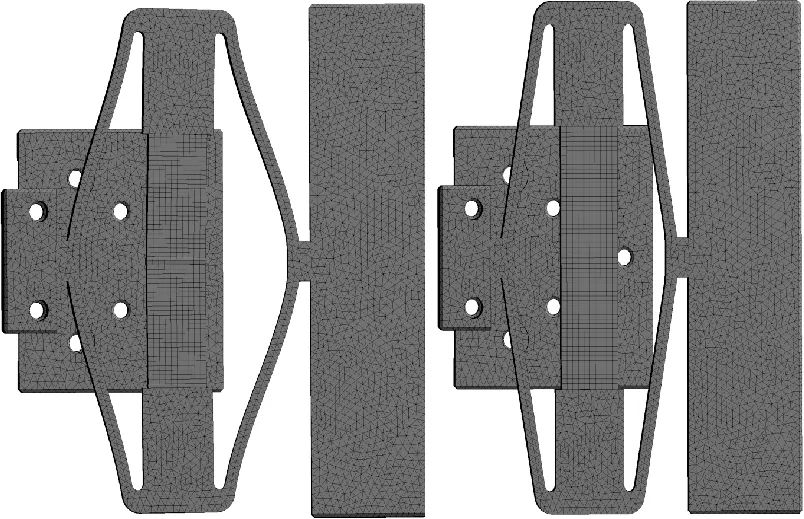
图4 驱动部分振动方式Fig.4 Drive part vibration mode

3.2 箝位部分模态分析

图5为箝位开关谐振模态仿真结果，箝位定子采用65锰钢，压电叠堆采用PZT-4。通过模态仿真分析得到箝位开关的三阶谐振频率为569 Hz，设计时保证箝位部分与驱动部分谐振频率近似，使两者能同时于谐振态工作。

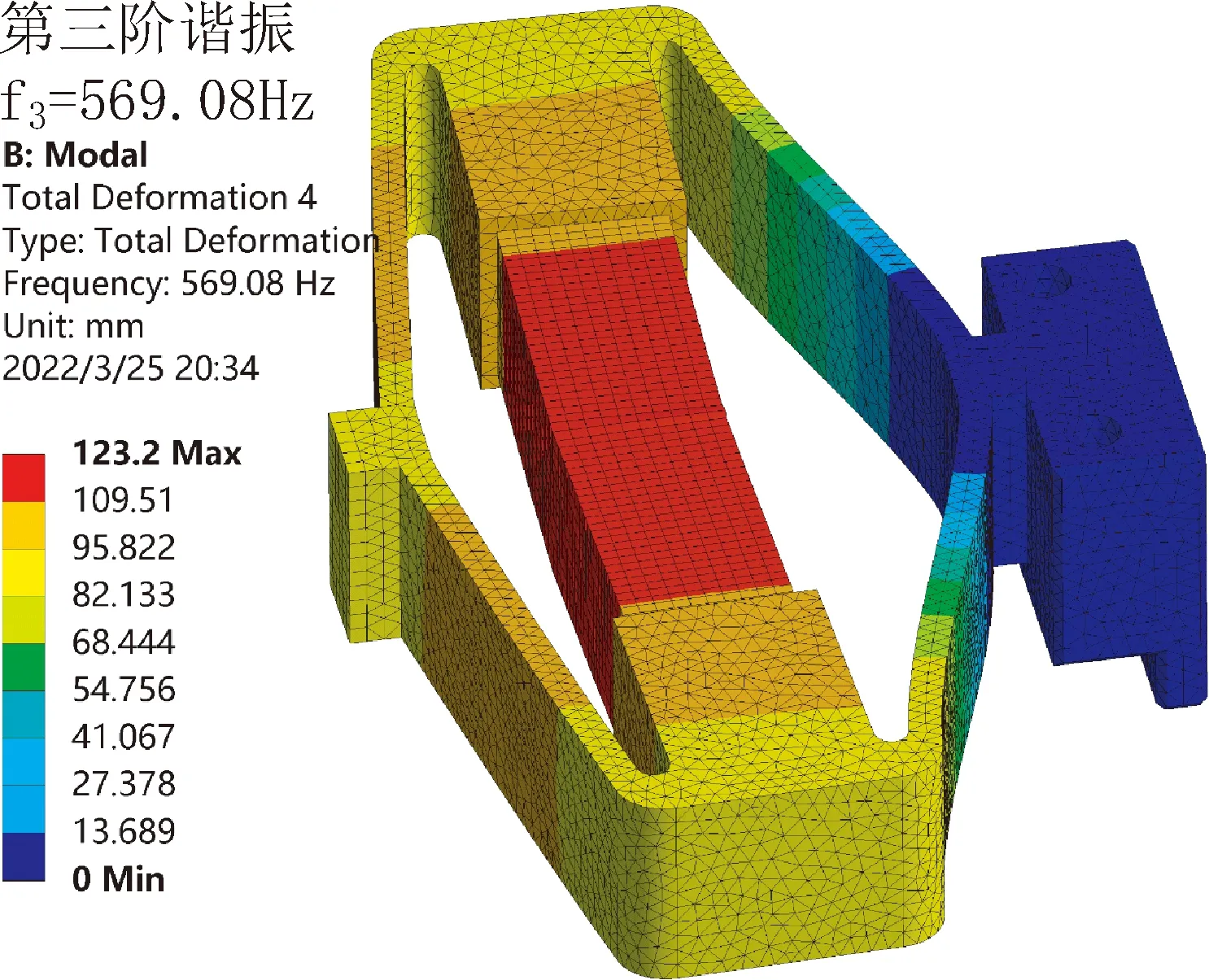
图5 箝位部分三阶谐振模态的ANSYS仿真Fig.5 ANSYS simulation of the third resonant mode of the clamping part

此阶谐振频率做图6形式的振动，该振动方式在配合工作过程中可对滑台起到较好的箝位作用。

图6 箝位定子振动方式Fig.6 Clamping stator vibration mode

4 实验测试与分析

4.1 实验装置

图7所示为箝位式压电马达实验装置，通过信号发生器(DG1022U)的通道1、通道2产生2组正弦形式激励信号，再经功率放大器(LYF-800AS)将两信号电压值放大，结合数字示波器(TBS1102B)监测的电压值，调节功率放大器旋钮获得所需电压值。利用激光位移传感器(optoNCDT2300)记录多组实验数据，再用matlab进行数据处理，获得滑台上端盖速度特性。

实物如图8所示。

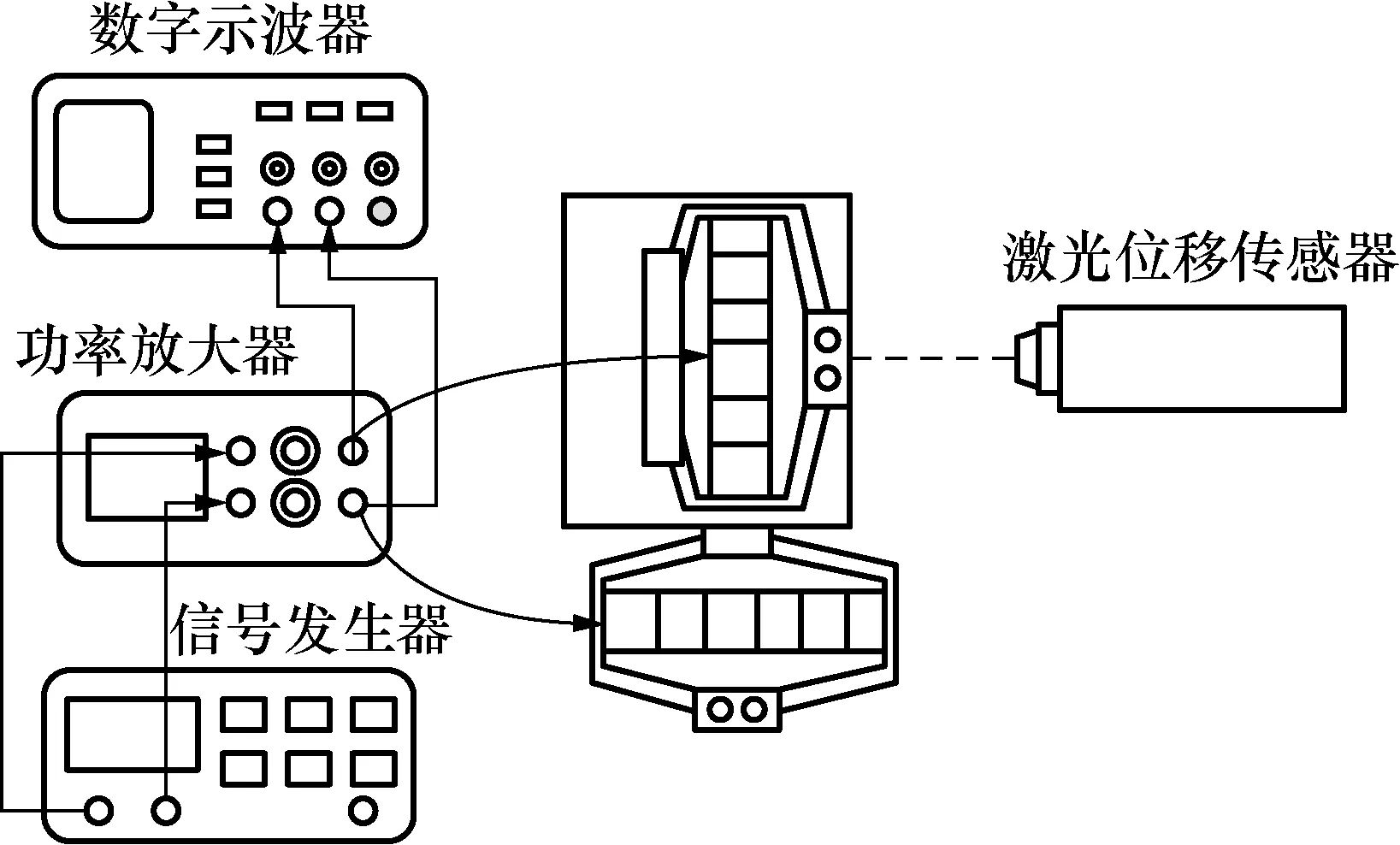
图7 实验装置Fig.7 Experimental facility

图8 实物图Fig.8 real products

4.2 步进运动特性

4.2.1 准静态运动特性

图9为改变激励电压的马达无负载运动步距特性，图10为激励电压改变时对应的步进速度曲线。在激励频率为250 Hz,箝位部分激励滞后于驱动部分激励 π/ω时，随着激励电压的提升，步距和速度均得到提升，且速度随着激励电压信号幅值的增长呈线性增长趋势。该马达在电压Vp-p为10 V时,步距约为0.5 μm，速度约为0.13 mm/s；在电压峰峰值Vp-p为70 V时,步距约为5.8 μm，速度约为1.52 mm/s。

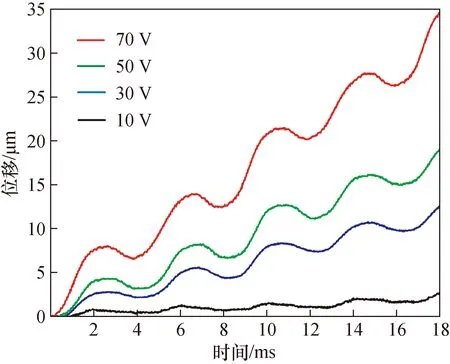
图9 准静态不同电压下位移与时间关系曲线Fig.9 Quasi-static displacement and time curves under different voltages

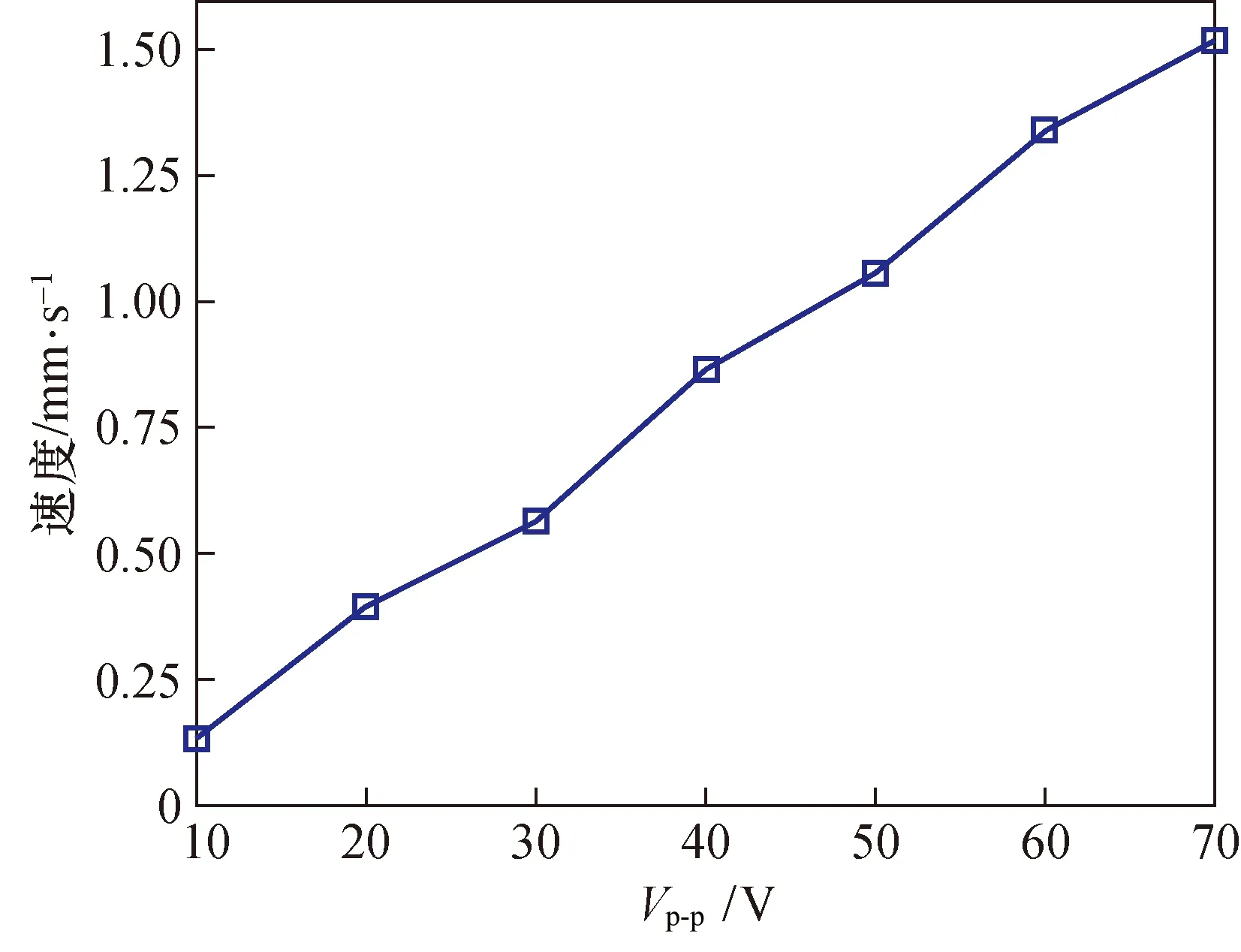
图10 准静态步进速度与电压关系曲线Fig.10 Quasi-static step speed and voltage relationship

图11为准静态时改变激励信号频率对步进特性的影响，当马达工作于准静态时改变激励频率步进速度会得到提升。

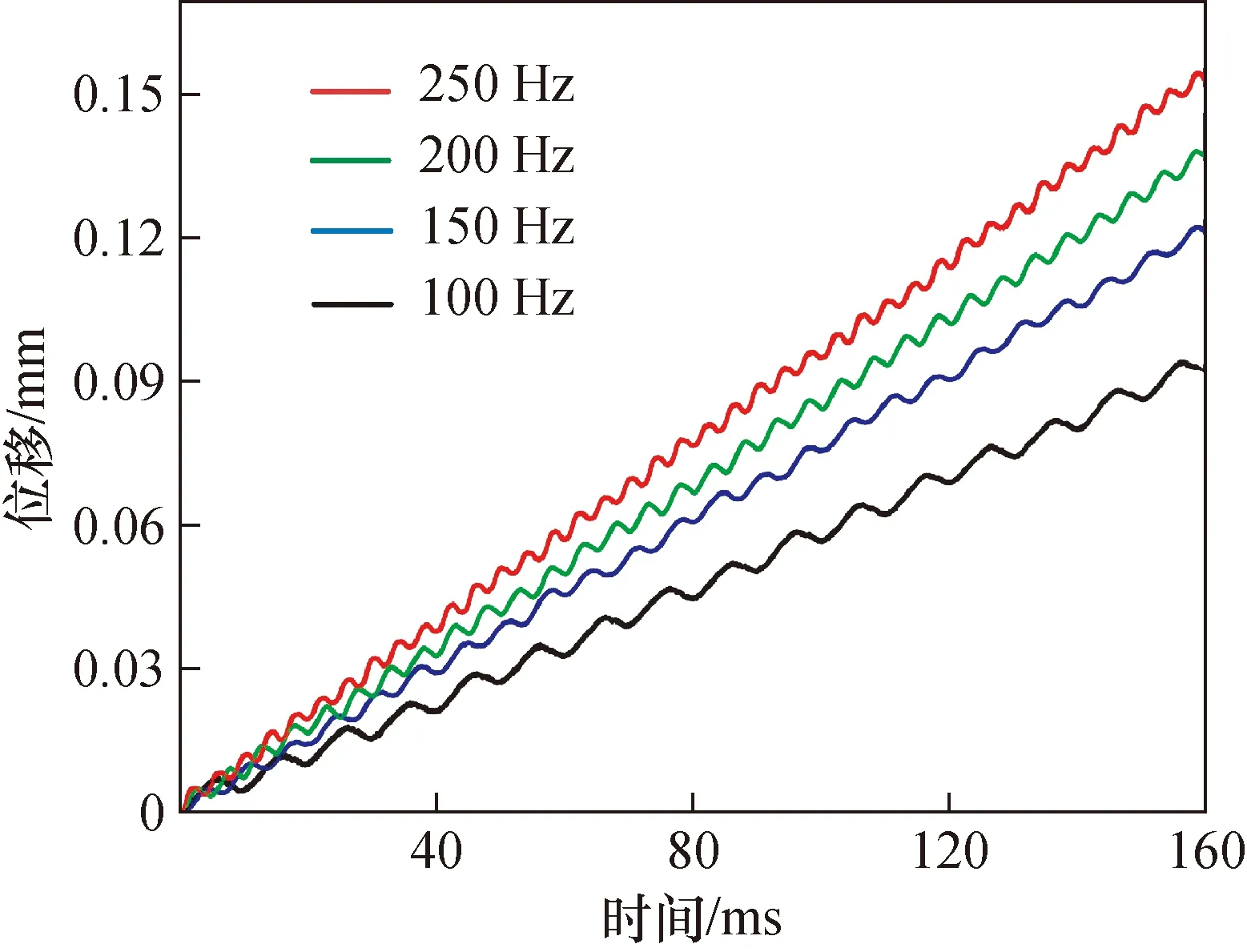
图11 准静态不同激励频率下步进运动特性Fig.11 Quasi-static stepping motion characteristics under different excitation frequencies

4.2.2 谐振态运动特性

根据振动力学，当马达工作于谐振态时箝位部分与驱动部分分别受到自身系统物理参数的影响使得两者位移波形相比于激励信号产生不同程度的相位偏差，导致两者最佳的配合状态不再是激励信号相差 π/ω。

如图12所示，电压峰峰值Vp-p为50 V时，改变箝位部分激励信号的滞后角度，观察其对步进速度的影响。当箝位部分激励信号滞后于驱动部分激励信号93°时，马达步距达到最大值22 μm,且速度达到最快11.3 mm/s 。

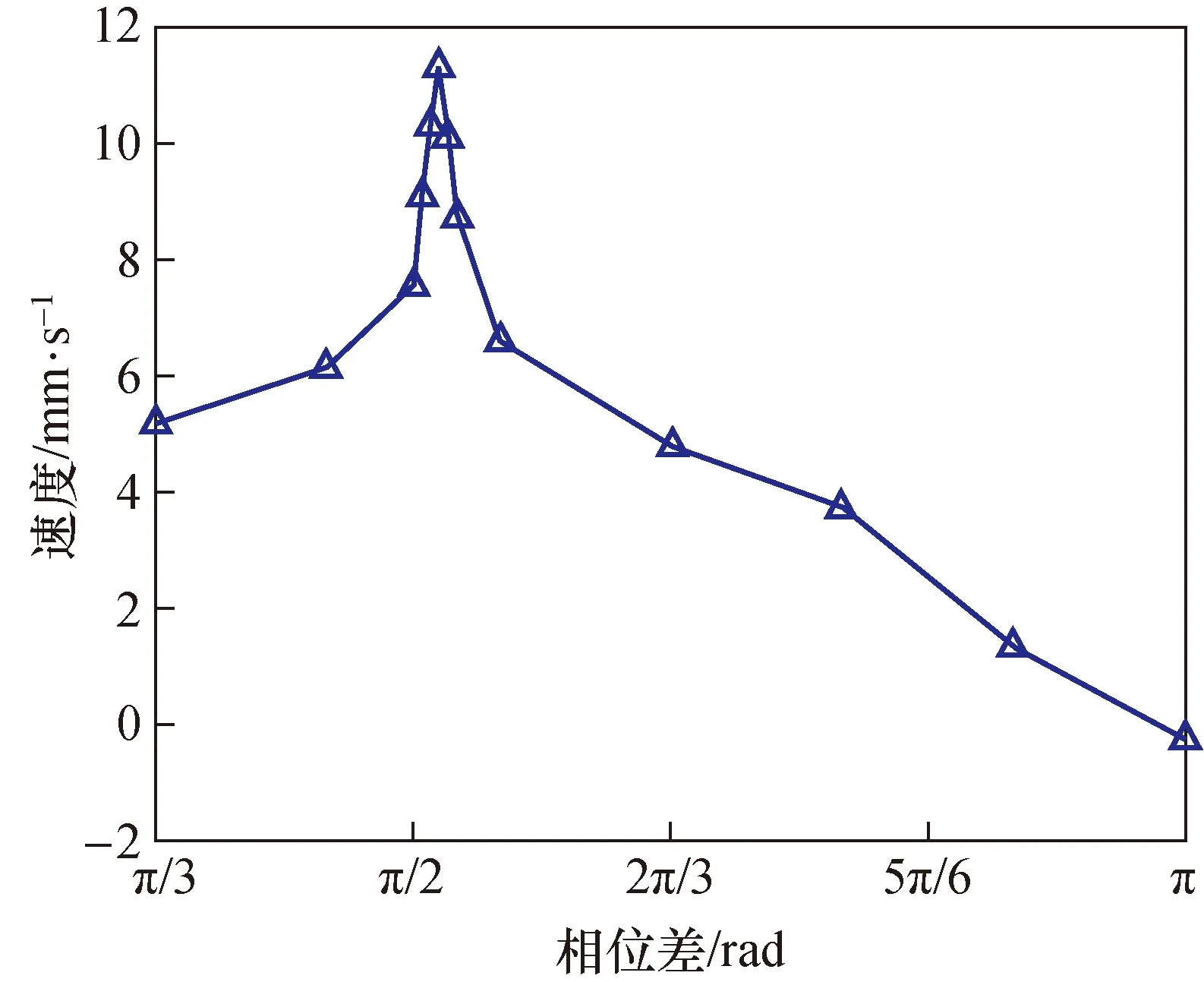
图12 谐振态步进速度与相位差关系曲线Fig.12 Relation curve between resonant state step velocity and phase difference

如图13所示，谐振状况下改变激励电压时步进速度同样会得到提升，当电压峰峰值Vp-p为70 V时步进速度达16.9 mm/s，步距达32 μm，相比于准静态时的运动速度大大提升，实现了跨尺度运行。

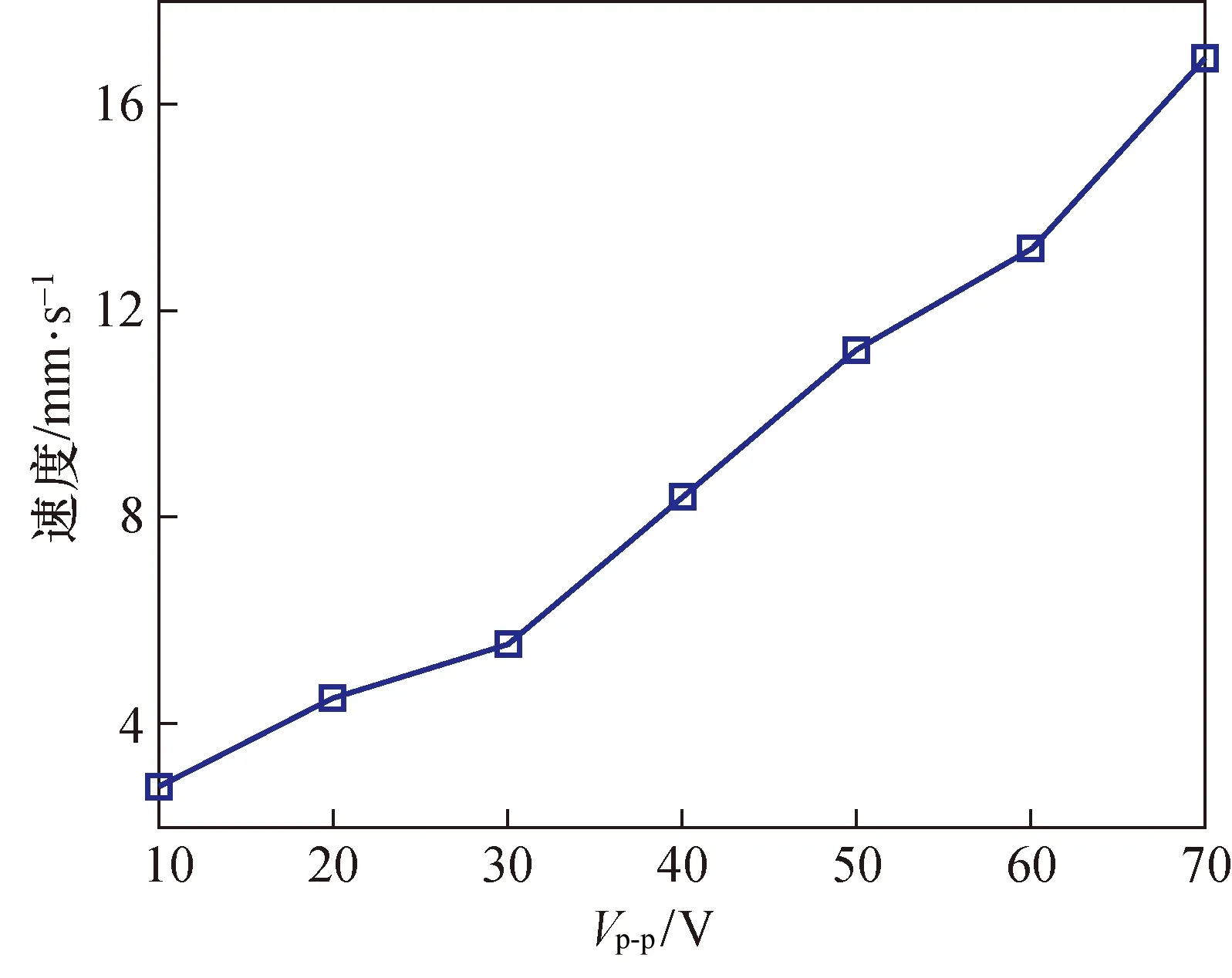
图13 谐振态步进速度与电压关系曲线Fig.13 Resonant stepping speed and voltage relationship curve

4.3 箝位波形研究

本文认为箝位部分可采用正弦波替代方波做激励信号，展开如下实验：在准静态下，用300 Hz、电压峰峰值Vp-p为50 V的正弦波与方波信号分别激励箝位部分，同时驱动部分保持300 Hz、电压峰峰值Vp-p为50 V的正弦激励，获得驱动部分位移波形如图14所示。图14(a)为正弦波做箝位激励信号，图14(b)为方波做箝位激励信号，两者波形虽有差别，但步距基本无区别，宏观上两者速度基本无差别。实验结果表明正弦波于准静态下可取代方波作为箝位部分激励信号且仍能满足高分辨，于谐振态下工作时可突破方波波形失真的限制实现马达高速输出。

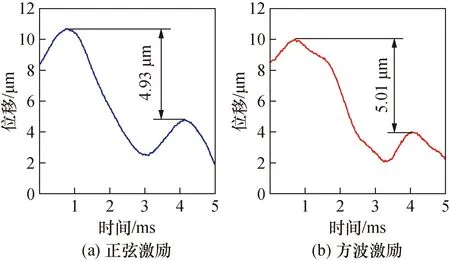
图14 准静态下不同箝位激励波形时驱动位移波形Fig.14 Driving displacement waveform with different clamped excitation waveform under quasi-static condition

5 结 论

本文针对箝位式压电电机箝位部分结构设计复杂、无法于谐振状态工作的缺点，提出采用正弦波作为箝位部分激励信号的方式代替锯齿波，大大简化箝位部分结构的同时还可保证压电马达能于谐振状态工作。

改进后的压电马达于准静态250 Hz、电压峰峰值Vp-p为10 V时,步进距离为0.5 μm，步进速度约为0.13 mm/s;谐振态540 Hz、电压峰峰值Vp-p为70 V时,步距为32 μm，步进速度达16.9 mm/s，兼顾了低频高分辨率和高频高速输出以实现跨尺度工作。该研究对降低压电马达设计难度、拓展压电马达兼顾准静态高分辨和谐振态高输出研究思路具有重要意义。