一种面向卷烟混合生产线的优化调度模型研究

何文婕，许玉江，闫浩峰，颜炳岩

一种面向卷烟混合生产线的优化调度模型研究

何文婕，许玉江，闫浩峰，颜炳岩

（河南中烟工业有限责任公司洛阳卷烟厂，河南 洛阳 471000）

基于多品种、小批量的生产制造模式，在规定的8 h工作之内，快速有效地生产出多品种、多批量的卷烟，并对所需物料进行准确调度，达到经济效益最大化的目的。针对某烟草生产企业订单需要生产6种型号的品牌香烟，通过分析卷烟生产线的工艺流程，提出一种解决卷烟厂车间资源优化调度的CSS模型，该模型可以根据产品之间的销售需求情况来匹配生产线资源配置，按需求比采用粒子群优化算法计算出单次投料后混合生产香烟所需的最小时间与最大收益。将所得方案进行综合对比后，计算得出在规定工期内，生产香烟获取利益的最优分配方案，在迭代在10次以内时已完成了优化过程，最大获利为3.65万元。该优化模型通过改变相关工艺参数能够实现对不同混合生产线的资源调度优化，并对其他制造行业提供借鉴价值。

粒子群优化算法；卷烟；车间资源

现阶段，我国制造企业车间生产已经日益实现智能化和自动化，人工智能的出现更是促进了自动化生产的集成程度，极大的减少了人力和物力消耗，同时提高了生产效率。卷烟生产线即是典型的连续生产的工业系统，其工作方式采取流水线智能制造和装配作业，所在生产线的生产效率高低和产品质量优劣直接影响着卷烟厂的经济效益和社会地位。

随着市场用户对产品的多样化要求越来越高，即每条生产线需要在一条线上生产多种品牌的香烟，根据客户的实际需要，基于定单生产的多品种、小批量的生产方式已经成为当今卷烟企业的制造模式之一，如何在规定的8小时工作之内，快速有效的生产出多品种多批量的卷烟并对所需物料进行准确调度是当前亟须解决的主要问题。国内外研究学者对此问题进行了深入研究和探讨。Azizoglu等[1]对多级混合生产流水作业的车间调度问题提出了一种分支定界的求解算法，该算法针对中等规模问题的最优求解颇有成效。Jenabitsw等[2]以最小化单位时间的切换和库存成本最小为目标函数，以带不相关并行机的柔性流水车间的批量制造和资源调度问题进行了研究，针对小规模生产问题提出了一种全新的数学规划模型。Marcus等[3]采用启发式算法对混合型卷烟制丝排产的资源调度问题进行了计算，并取得了较好的优化效果。吴小超等[4]针对烟草行业使用的设备卷包机组，提出了一种结合OEE的设备效率评价体系以实现对卷包机组设备运行状态的精确反映，在该体系支持下，设备净效能实现了精准高效管理。王晓红等[5]提出了一种基于莱维飞行发现概率的变步长布谷鸟搜索算法用以解决求解复杂高维函数优化问题，并解决了求解精度不够高和易陷入局部最优等问题。吴敏亚等[6]指出了应用MRPII系统的技术要求及在烟机制造业中取得的成效。郑锋等[7]研究了混合型企业生产调度的研究现状、存在问题和解决途径。王伟玲等[8]在保证按时交货的前提下，通过建立多目标混合整数规划模型，调整加工产品顺序与实际数量，获得了各种加工成本与换牌时间最少的目的。王爱民等[9]提出了涵盖移动调整、订单追加和二次调度的烟草卷包作业动态调度技术体系，以解决现场执行与作业计划同步的问题。吕希胜等[10]通过某烟厂的制丝线项目并基于.Net技术提高了生产质量和效率。江逸斐等[11]提出基于MES系统支持的高效卷烟生产调度方法并用来提高卷烟生产的调度能力。李家斌等[12]建立了总成本费用最小的卷烟包装箱回收物流系统调度优化模型，利用CPLEX得到闭环物流系统网络最优调度方案。徐晓光等[13]建立了以最小化单位最终产品综合能耗和单位最终产品总能源消耗成本为目标的卷烟企业能源平衡调度模型，较好地解决了卷烟企业的能源平衡调度。Jaszkiewcz等[14]采用多目标遗传局部搜索算法，获得了进化过程中随机分配每个优化目标对应的权系数。Ishibuchi等[15]通过联赛选择机制确定局部搜索的初始解，指定了局部捜索的进化方向。上述研究集中聚焦在采用先进智能算法和优秀管理方法并提高产品生产效率和产量上，对于粒子群算法应用在卷烟企业的多品种多批量的资源调度管理尚未触及。

为在规定的8小时（等同于后续模型算法算法中的一次迭代）工作之内，快速有效的生产出多品种多批量的卷烟并对所需物料进行准确调度，满足快速迅捷的市场需求，达到经济效益最大化的目的。针对某烟草生产企业订单需要生产6种型号的品牌香烟，通过分析卷烟生产线的工艺流程，提出了一种解决卷烟厂车间资源优化调度的CSS模型，该模型可以根据产品之间的销售需求情况来匹配生产线资源配置，按需求比采用粒子群优化算法计算出单次投料后混合生产香烟所需的最小时间与最大收益。将所得方案进行综合对比后，计算得出在规定工期内，生产香烟获取利益的最优分配方案，在迭代10次以内时完成优化过程，最大获利为3.65万元。该优化模型通过改变相关工艺参数能够实现对不同混合生产线的资源调度优化，并对其他制造行业提供借鉴价值。

1 问题描述

卷烟厂的车间调度问题是一个十分典型的目标优化问题，需要考虑的影响因素众多，例如生产车间如何安排烟卷的生产过程，实现生产线的最高装配效率、怎样安排不同类型的烟卷制造和实现最大获利等。卷烟生产线的主要工序包括下料、投料、真空回潮、加辅料、储叶、切叶、切梗、烘丝、储丝、卷接包（卷烟、接过嘴、包装）等工序（图1），因烟草机械具有高度自动化、高度智能化的特点，同时具有集成程度高、模块化程度严重等特征，在正常生产时要求各个工序间保持均衡发展，实现物料流动单向不可逆，无循环环节。

每包成品卷烟的生产过程由很多个作业单元或作业工序构成。实现不同作业单元的消耗时间是不同的，不同类型的香烟在生产过程中实现不同的作业单元所消耗的作业时间也是不同的，因此在一段工期时间内，结合现实过程中对不同类型香烟的需要，如何高效率完成烟卷的制造和装箱（车间调度的最小消耗时间），并获取最大的利润是一个很重要的问题。

1.1 某卷烟厂基础生产关系

图1 香烟制作工艺流程

即总需求表达式为，

需要在有限的时间条件下完成卷烟制造作业的合理分配，并确定这批次卷烟的生产顺序，从而达到实现卷烟总装时间最小的目的。

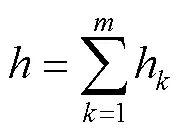
一般的，一个排序循环只是对一个比例集合中的所有产品进行排序。实际中，当循环次数达到次时，即完成了对个产品的排序。

1.2 多类型向单类型的转化

多类型向单类型转化是作业分配的基础，通常主要有如下2个方面。

1.2.1 作业时间的转化

不同类型的作业综合后将时间整合为一个任务作业，分散的时间也统一规划为一个时间，又称作为平均时间，用表示。将作业的第个作业单元在第种类型香烟中的作业时间设为，综合后的第个作业单元的作业时间为：

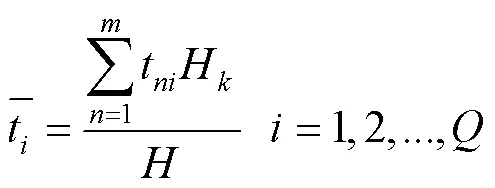
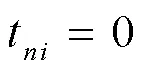
1.2.2 优化过程中关系的转化

综合不同种香烟优先关系矩阵的行列位置上的元素为：

综合处理后的香烟优先关系矩阵为：

通过综合香烟的作业优先矩阵，可以计算得到符合作业优先关系的合理作业序列，并可以根据平均作业时间和装配线节拍时间来确定一个作业方案。

2 Cigarette Shop Scheduling（CSS）模型的建立

针对此类问题，提出了一种烟厂车间调度CSS模型，针对车间应对多品种，多批量中对不同类型香烟的需求，在保证最高生产效率（最小生产时间）的情况下，基于粒子群优化算法，得到卷烟厂的最大化收益情况。

2.1 基于主层次分析法分析香烟需求量的大小

卷烟厂的生产不仅要考虑生产效率，也要注意不同种类香烟的需求。根据香烟实际需求量的关系情况，通过主层次分析法计算出不同类型香烟的权重，并按照比例处理后得到更为贴近实际的需求量之比。

2.1.1 构建层次分析模型

改进型层次分析法在分层上有所不同，其主要由总目标层、分目标层、准则层以及方案层4层[16-17]组成。对香烟需求量大小进行排序时，可以将单位时间内香烟实际的售卖（产量）情况设为最高目标层，且只有一个元素。

为了能够满足各目标层的相关准则，建立每种因素之间的相互关系以及不同层次之间的隶属关系，并根据相关的准则将不同的元素进行分组，确定不同层次上的支配关系。

2.1.2 建立判断矩阵

通过不同层次之间的结构关系可以构造判断矩阵，根据相关要求对多类型之间的需求量进行比较，并定量赋值，见表1。

表1 相对比较标度

Tab.1 Relative comparisonscale

2.1.3 计算权重

通过判断矩阵确定各因素对其需求准则的权向量，并采用和法进行计算，一致性矩阵通过各列归一化处理得出：

式中：W为权重；a为准则元素；a为传递矩阵元素。

2.1.4 进行一致性检验

2.1.5 比例处理

通过一致性检验的权重数据可以继续使用，将权重大小的中间值m成比例扩大为1，计算得到的扩大系数b与各个权值相乘得到实际需求量之比，

式中：qi第个类型产品的需求量；W为第个类型香烟的权重；为每次加工原料的质量。

2.2 车间调度模型的建立

烟草的生产过程中需要完成很多步工序，并且一个生产线在生产的过程中也可以混合生产很多不同种类的烟卷，因此如何决策烟卷的生产也变得十分重要，需要求出满足实际需求条件下的最小生产时间。首先对车间调度模型参数进行说明，见表2。

根据车间调度问题的描述和约束条件的假设，对混合装配线模型进行了优化，其中的变量定义见表3。

首先需要确定分配方案，为了保证了一个作业单元只能被分配到一个工位中去，建立式（12）。

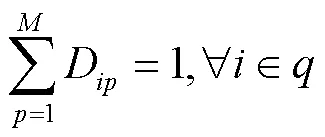
表2 模型参数说明

Tab.2 Description of model parameters

表3 决策变量定义

Tab.3 Definition of decision variable

所有的作业元素都需要完成分配过程，

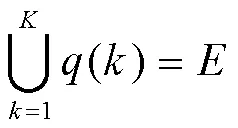
在不同的作业单元中需要满足优先顺序的约束关系，

每一个工位的平均负荷不能够超过这个工位所对应的节拍时间，并且需要保证排序后的序列上只能够存在一种产品，相关符号说明见表4。

确定分配方案后还需根据资源情况来满足作业集的约束条件，最后再分配到一个工位中去。

表4 符号说明

Tab.4 Symbol description

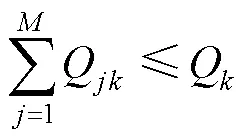
式（16）表示分配方案作业集中需要使用到的固定设备；式（17）表示完成某项作业使用到的固定设备工位；式（18）中表示分配方案中安排的流动设备工位情况；式（19）保证配备到所有工位的流动设备总数不超过流动设备的可用数量；式（20）表示当分配的方案对工种有需求时，应当取其最大数量，并分配到满足数量要求的工位中去；式（21）表示所有工种分配到每一个工位的数量不能超过这个工种的实际可用数量。

多品种的排序约束条件为：

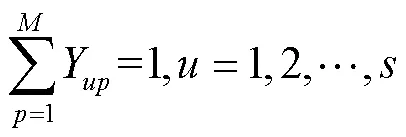
式（22）表示在一个序列中的产品只能够占据1个位置；式（23）保证了排序产品在某一位置上的产量等于该类型产品的需求量。

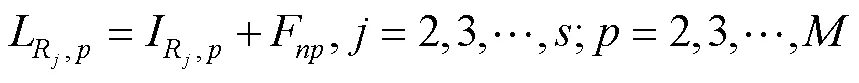
2.3 卷烟厂的最大获利

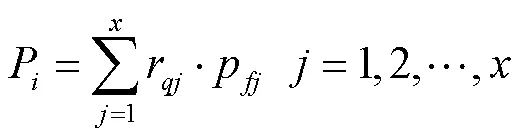
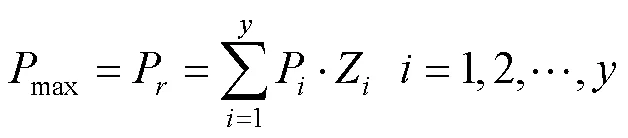
2.4 粒子群优化算法

粒子群优化算法（PSO）是一种源于模拟鸟类捕食行为的算法，首先通过将一群随机粒子初始化，接着进行迭代从而得到最优解。在每一次的迭代中，粒子都可以通过对两个“极值”的跟踪来更新自己。其中一个“极值”是粒子本身找到的最优解，即个体极值；而另外一个是从整个种群中得到的最优解，即全局极值。

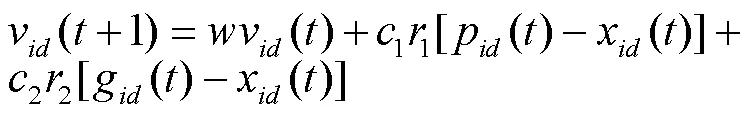
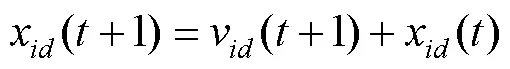
式中：为1、2正常数，称为加速因子；1、2为[0,1]之间的随机数；为加权系数，取值在[1,0.9]。

粒子通过不断地学习与更新，最终移动到解空间中最优解所在的位置，此时搜索过程结束，并输出全局最优解。在粒子每一次更新的过程中，其运动速度与位置也都会受到限制，一因此粒子必须在允许范围内才能够一次更新。

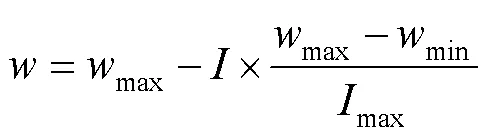
3 实例分析

卷烟生产线是卷烟厂的主要生产线，主要流程见图1，由投料、真空回溯、打叶、加辅料、储叶、切叶、烘丝、储丝、卷接包（卷烟、接过嘴、包装）等作业单元组成。各个作业单元之间的生产节奏均匀，并且物料上的生产都是连续的，因此烟卷的生产线是一个十分典型的流程型工业系统。（引用柔性优化调度模型）

根据上述算法结合某市烟草公司实际订单进行分析，调用Access数据库订单，某卷烟企业的生产车间可以生产10种烟草品牌，这里重点选用6种，分别为黄金叶、帝豪、红旗渠金渠、红旗渠普渠、大天叶、小天叶，在一定时间内，同一条装配线上配置生产不同类型烟卷产品，以此以代号A、B、C、D、E、F代替，并结合卷烟厂的生产相关状况得到表5，

使用Matlab编程采用粒子群优化算法进行求解。同时采用LabVIEW来验证上述自动算法的可行性，这是一个功能强大且灵活的软件，LabVIEW（Laboratory Virtual instrument Engineering Workbench）是一种用图标代替文本行创建应用程序的开发环境，它被科学家和工程师应用来达到解决问题的目的。其拥有的函数库功能强大，里面包含了数据显示，GPIB等等，还内置了便于应用TCP/IP、ActiveX等软件标准的库函数，可以在很短的时间内被掌握和实践，非常适合工程师，技术员等人的使用通过CSS模型进行分析。在文中，按照设计的卷烟自动优化模型，将实际需求和产量订单进行“虚拟容器”排列，并计算订单中相应品牌的卷烟进行正常生产的作业时间，形成时间控制和需求矩阵，使自动生产线机在正确的时间准确无误的将各品牌的卷烟产出。

由ACCESS数据库导出6种烟卷的实际销售排名，顺序由高到低分别为A、E、C、F、D、B，该数据库来源于企业的市场部门，通过式（1）—（11）对不同类型卷烟销售关系进行相关分析，同时结合LabVIEW，按照对应的换算比例综合考虑，得到6种卷烟的车间需求情况（表6），只有这样生产才能保证市场的时间需求，并达到利益最大化。

表5 生产线与香烟品牌产量关系

Tab.5 Relationship between production line and cigarette brand output

表6 不同类型香烟需求表

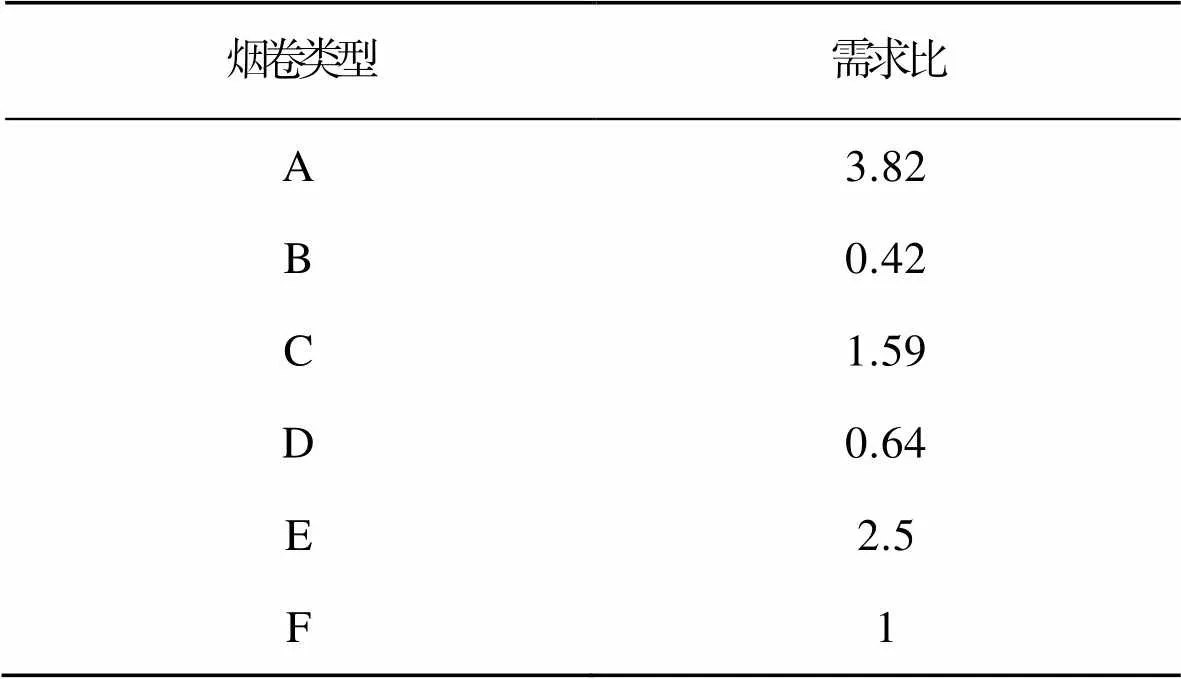
Tab.6 Demand of different types of cigarettes

根据上述分析，每一批次卷烟的生产初试投料约为150～250 g，当取A、B、C、D、E、F这6种卷烟按照表1比例进行生产制作，卷烟的生产关系见图2。

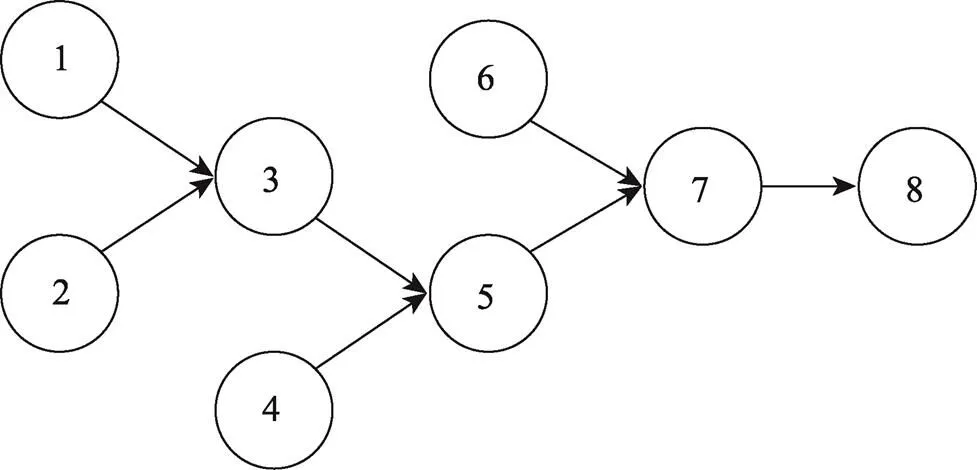
图2 卷烟生产关系图

图2中序号表示卷烟生产的顺序步骤：①表示烟草的生产；②表示卷烟纸的生产；③表示烟草与卷烟纸的组装；④表示烟头的生产；⑤表示烟支与烟头的组装产出整烟；⑥表示烟盒的生产；⑦表示整盒烟的生产；⑧表示整盒烟集装成条。

通过文中的算法可以求得本批次混合生产卷烟的最小生产时间为26.4 h，能够获得收益1.25万元。将生产方案的相关情况表示见表7。

表7 生产方案耗时–利润

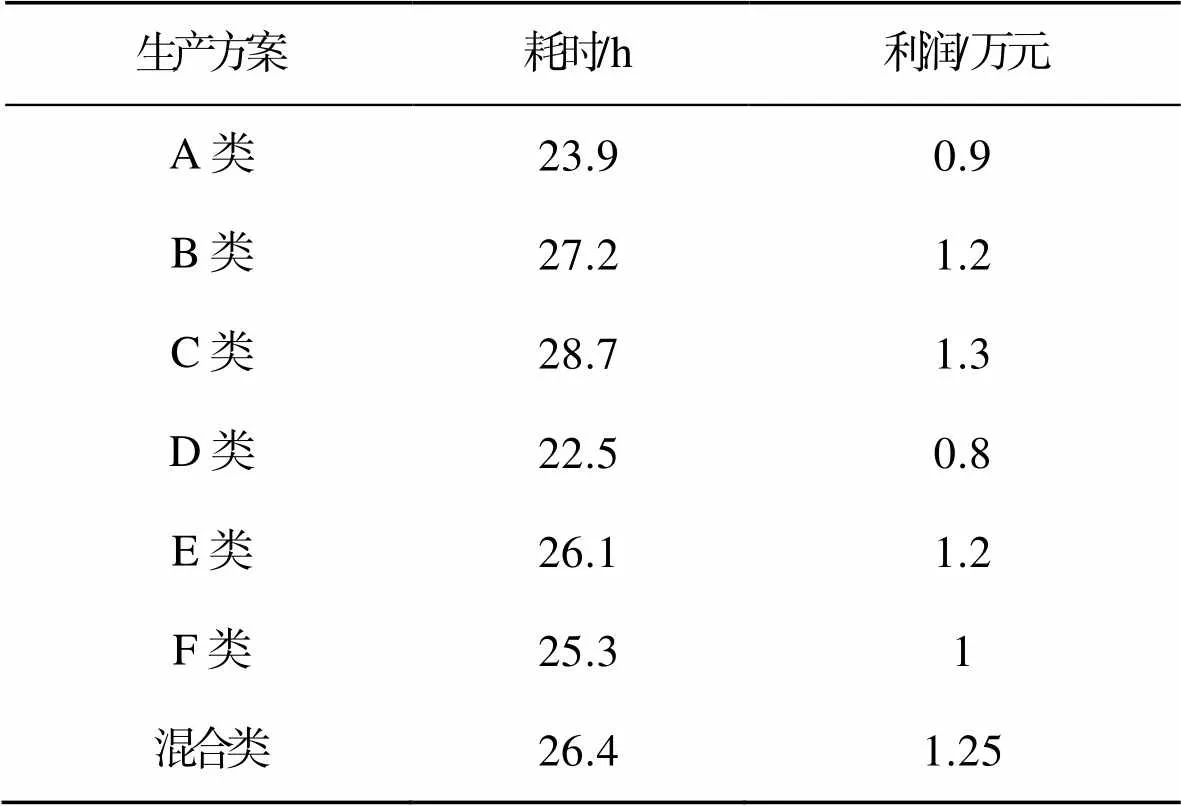
Tab.7 Time consumption and profit of production scheme

相关数值代入到CSS模型中，通过Matlab使用粒子群优化算法对CSS模型进行求解，得到了混合生产方案的消耗时间与利润。将6种香烟的生产方式与混合后的生产方案均作为车间工作的实行方案，在规定工期内（假设每日工作时间为8 h，一次迭代）对不同的生产方案进行选择，得到收益最大的决策方案（表8）。所得方案进行56、72、80 h迭代后进行综合对比，分别得到图3—5，经对比分析，得出在最优方案为80 h之内，生产香烟获取利益可得到最优分配方案，在相同投料结果基础上迭代在10次可完成优化过程，最大获利为3.65万元，

表8 工期时间内优化生产方案

Tab.8 Optimization of production scheme within the construction period

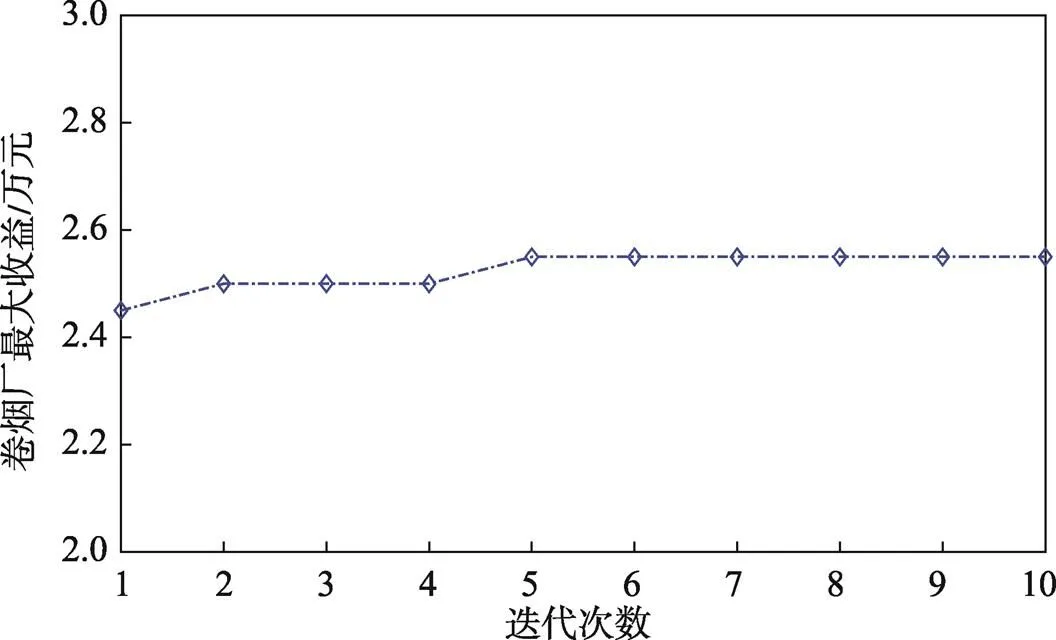
图3 任务工期为56 h的优化结果

图4 任务工期为72 h的优化结果

图5 任务工期为80 h的优化结果

算法模拟迭代次数初始值设为100次，加速因子数均为1.5，加权因子最大最小值分别为0.8、0.4，速度极值为±10。根据图像结果可得知在迭代在10次以内时已完成了优化过程（图像为10次迭代的收益图），求得了不同工期时间的优化结果（最大收益），有效解决了烟厂生产不平衡，产量不满足的问题。

通过以上分析得到了基于粒子群优化算法的CSS模型的优化结果，为了更好地对各个算法的优化结果进行分析，文中引入SA以及NSGA–Ⅱ 2种算法，设工作总时长为500 h，计算得到3种算法的优化结果，见表9。

表9 工期时间内优化算法对比

Tab.9 Comparison of optimization algorithms within task duration

由表8可知，文中提出的CSS模型计算的方案实际消耗时间最小、实际收益最大，优化程度大于SA算法、NSGA–Ⅱ算法。

4 结语

1）提出了一种解决卷烟厂车间资源优化调度的CSS模型，该模型可以根据产品之间的销售需求情况来匹配生产线资源配置，按需求比采用粒子群优化算法计算出单次投料后混合生产香烟所需的最小时间与最大收益。

2）所得方案进行56、72、80 h迭代后进行综合对比，得出在最优方案为80 h之内，生产香烟获取利益可得到最优分配方案，在相同投料结果基础上迭代在10次可完成优化过程，最大获利为3.65万元，同时有效解决了烟厂生产不平衡，产量不满足的问题。

3）该优化模型通过改变相关工艺参数能够实现对不同混合生产线的资源调度优化，可拓展应用于更多类型的烟厂车间调度模型中，增加迭代次数并改变相关参量能够对更多目标进行优化，是一种适用型极强的新型模型。

[1] AZIZOĞLU M, ÇAKMAK E, KONDAKCI S. A Flexible Flowshop Problem with Total Flow Time Minimization[J]. European Journal of Operational Research, 2001, 132(3): 528-538.

[2] JENABI M, GHOMI S F, TORABI S, et al. Two Hybrid Meta-Heuristics for the Finite Horizon ELSP in Flexible Flow Lines with Unrelated Parallel Machines[J]. Applied Mathematics and Computation, 2006, 186(1): 230-245.

[3] PATTLOCH M, SCHMIDT G, KOVALYOV M Y. Heuristic Algorithms for Lotsize Scheduling with Application in the Tobacco Industry[J]. Computers & Industrial Engineering, 2001, 39(3): 235-253.

[4] 吴小超, 张怡, 熊坚, 等. 卷包机组设备效率评价指标体系的设计与实现[J]. 包装工程, 2021, 42(13): 262-269.

WU Xiao-chao, ZHANG Yi, XIONG Jian, et al. Design and Implementation of Efficiency Evaluation System for Cigarette Production Machines[J]. Packaging Engineering, 2021, 42(13): 262-269.

[5] 王晓红, 杨礼彬, 任展翔, 等. 求解包装生产中复杂问题的布谷鸟算法改进[J]. 包装工程, 2021, 42(5): 240-246.

WANG Xiao-hong, YANG Li-bin, REN Zhan-xiang, et al. Improvement of Cuckoo Algorithm for Solving Complex Problems in Packaging Production[J]. Packaging Engineering, 2021, 42(5): 240-246.

[6] 吴敏亚, 张东森. 制造资源计划(MRPⅡ)在烟草机械企业的应用[J]. 成组技术与生产现代化, 2003, 20(2): 37-39.

WU Min-ya, ZHANG Dong-sen. The Application of MRPⅡ in Tobacco Machinery Enterprise[J]. Group Technology & Production Modernization, 2003, 20(2): 37-39.

[7] 郑锋, 孙树栋. 混合型企业生产调度问题综述[J]. 制造业自动化, 2004, 26(2): 1-4.

ZHENG Feng, SUN Shu-dong. Survey of Schedule Problem of Hybrid Process[J]. Manufacturing Automation, 2004, 26(2): 1-4.

[8] 王伟玲, 王晶. 卷烟多目标柔性流水调度问题[J]. 机械设计与研究, 2014(3): 97-99.

WANG Wei-ling, WANG Jing. Study on Scheduling Problem Multi-Objective Flexible Flow Ling for of Cigarette[J]. Machine Design & Research, 2014(3): 97-99.

[9] 王爱民, 丁雷, 宁汝新, 等. 烟草卷包作业动态调度技术[J]. 计算机集成制造系统, 2010, 16(3): 603-610.

WANG Ai-min, DING Lei, NING Ru-xin, et al. Tobacco Packaging Job-Shop Dynamic Scheduling Technology[J]. Computer Integrated Manufacturing Systems, 2010, 16(3): 603-610.

[10] 吕希胜, 史海波, 潘福成. 制丝线计划与调度系统研究与实现[J]. 制造业自动化, 2009, 31(1): 83-86.

LYU Xi-sheng, SHI Hai-bo, PAN Fu-cheng. Research and Realization on Planning and Scheduling System in Primary Processing Line of Cigarette Factory[J]. Manufacturing Automation, 2009, 31(1): 83-86.

[11] 江逸斐, 肖梦, 张永进, 等. MES系统支持下高效卷烟生产调度方法研究[J]. 计算技术与自动化, 2020(4): 154-158.

JIANG Yi-fei, XIAO Meng, ZHANG Yong-jin, et al. Research on High Efficient Cigarette Production Dispatching Method under Support of MES System[J]. Computing Technology and Automation, 2020(4): 154-158.

[12] 李家斌, 何世伟, 胡红春, 等. 卷烟包装箱回收物流系统调度优化模型[J]. 中国烟草学报, 2018(3): 106-112.

LI Jia-bin, HE Shi-wei, HU Hong-chun, et al. Optimized Scheduling Model for Logistics System of Reclaimed Cigarette Cases[J]. Acta Tabacaria Sinica, 2018(3): 106-112.

[13] 徐晓光, 朱道飞, 张孝涵, 等. 卷烟企业能源平衡调度模型与应用[J]. 计算机系统应用, 2015, 24(12): 260-264.

XU Xiao-guang, ZHU Dao-fei, ZHANG Xiao-han, et al. Application and Model of Energy Balance Scheduling in Cigarette Enterprise[J]. Computer Systems & Applications, 2015, 24(12): 260-264.

[14] JASZKIEWICZ A . Genetic Local Search for Multiple Objective Combinational Optimization[J]. European Journal of Operational Research, 2002, 137: 50-71

[15] ISHIBUCHI H, YOSHIDA T, MURATA T. Balance between Genetic Search and Local Search in Memtic Algorithms for Multi-Objective Permutation Flowshop Scheduling[J]. IEEE Transaction on Evolutionary Computation, 2003, 7: 204-223

[16] 金玉玲, 孙浩. 基于主层次分析法的黄山旅游景区管理水平测度[J]. 长春师范大学学报, 2019, 38(4): 90-93.

JIN Yu-ling, SUN Hao. Management Level Measurement of Tourist Huangshan Scenic Spot Based on Principal Analytic Hierarchy Process[J]. Journal of Changchun Normal University, 2019, 38 (4): 90-93.

[17] 崔铭, 李妍君. 基于层次分析法的城市电动自行车发展趋势研究[J]. 内蒙古农业大学学报(自然科学版), 2011, 32(4): 261-265.

CUI Ming, LI Yan-jun. The Research of Electric Bicycle Development Trend in the City Based on Ahp[J]. Journal of Inner Mongolia Agricultural University (Natural Science Edition), 2011, 32(4): 261-265.

Optimization Scheduling Model for Hybrid Production Line of Cigarette

HE Wen-jie, XU Yu-jiang, YAN Hao-feng, YAN Bing-yan

(Luoyang Cigarette Factory of Henan China Tobacco Industrial Co., Ltd., Henan Luoyang 471000, China)

Since the order-based multi-variety and small-batch production has become the manufacturing mode of enterprises, the work aims to produce multi-variety and multi-batch cigarettes quickly and effectively within the prescribed 8 working hours and to schedule the required materials accurately, so as to maximize the economic returns. According to the order of a tobacco production enterprise, 6 types of brand cigarettes were required to be produced. Based on the analysis of the process flow of the cigarette production line, a CSS model was proposed to solve the problem in resource optimization and scheduling in the workshop of a cigarette factory. The model could match the resource allocation of the production line according to the sales demand of products, and calculate the minimum time and the maximum profit of the hybrid production of cigarettes after a single feeding according to the demand ratio by the particle swarm optimization. After the comprehensive comparison of the obtained schemes, the optimal distribution scheme of profits from cigarette production within the specified time limit was calculated. The optimization process was completed within 10 iterations, and the maximum profit was 36 500 yuan. The optimization model can optimize the resource scheduling of different hybrid production lines by changing relevant process parameters, and can provide reference value for other manufacturing industries.

particle swarm optimization; cigarette; workshop resources

F270.7

A

1001-3563(2022)17-0298-10

10.19554/j.cnki.1001-3563.2022.17.039

2021–10–21

河南省科技攻关项目（202102210087）；郑州市科技局产学研项目（郑科函[2020]3号）

何文婕（1974—），女，本科，工程师，主要研究方向为物流信息化。

颜炳岩（1994—），男，本科，助理工程师，主要研究方向为信息化。

责任编辑：曾钰婵