新型无人仓AutoStore的货物合箱方法研究
杨玮,张子涵,张晓楠,马伟
新型无人仓AutoStore的货物合箱方法研究
杨玮,张子涵,张晓楠,马伟
(陕西科技大学 机电工程学院,西安 710021)
为减少AutoStore系统在共同存储策略下的订单处理时间,解决经营品类繁多,但仓储面积有限的企业货物存储问题。提出货物合箱的存储方法,设计关联规则挖掘算法与混沌种子优化算法的混合优化算法进行求解。从机器人翻箱操作、料箱的分配规则、系统布局三方面进行分析,结合AutoStore运作规律,建立以机器人拣货行走距离最短为目标函数的数学模型,通过Apriori算法输出货物热度,输入混沌种子算法,得到储位分配结果,实现联动决策。在基本种子算法的迭代中加入混沌序列,帮助种子避开局部极小值。实例分析表明,货物合箱方法能够显著减少共同存储下AutoStore系统的订单处理时间,缩小与指定存储策略订单处理时间的差距,与粒子群算法和基本种子优化算法相比,混沌种子优化算法的优化效率更高、稳定性更好。文中的研究为经营品类繁多,但仓储面积有限的企业提供了一种更适合的货物存储策略,具有较强的操作性和实际意义。
AutoStore系统;存储策略;Apriori关联规则挖掘算法;混沌种子优化算法
机器人履行系统在世界各地的仓库中变得越来越普遍,AutoStore系统作为新兴的移动机器人履行系统(Robotic Mobile Fulfillment System, RMFS),具有超高空间利用率、高流量、运行稳定的优势,适用于目前蓬勃发展的电商企业、店仓一体化的大型零售商超,以及有大量拆零拣选或小批量多频次拣选任务的企业,AutoStore系统在国内外都具有广阔的使用空间[1]。典型的使用案例包括英国零售商超Asda、美国全渠道电子商品零售商Best buy、德国西门子公司等。国内首个AutoStore系统于2020年6月在北京投入使用。与传统自动化立体仓库不同,AutoStore不必留有巷道空间,而是由一列列形状规格相同的料箱叠加码放形成的高密度存储区,人们把一列料箱称为一个堆栈。机器人在网格货架的顶部沿–方向移动,配合提升机抓取和释放料箱,拣选网格货架中的货物。若待拣选货物所在料箱不位于货架顶层,而是位于堆栈的较深层次,则机器人需要进行翻箱。仓储系统的存储策略决定了仓库所需的存储空间和机器人执行系统的效率,由于AutoStore系统出现时间短,目前关于它的研究仍处于起步阶段,很少有文献可以指导决策者为操作这样的系统选择正确的存储策略,因此对系统存储策略展开研究十分必要。
过往针对存储策略的研究主要围绕随机存储和分类存储2种网格分区的方法展开,朱杰等[2]研究了随机存储策略下M/G/1随机服务系统的服务效率问题,提出2种货物拣选方式及其适用条件。Francisco等[3]针对具有随机存储和不同类型叉车仓库中的存储和检索问题,将其分解为托盘集合位置、叉车的任务分配、作业顺序等3个子问题,分别设计3个启发式算法进行求解。刘恺文等[4]研究了自动化立体仓库在随机存储和定位存储2种策略下的出入库调度问题。Eder[5]以基于穿梭车的存储和检索系统为研究对象,通过应用基于类的存储策略提高系统最大吞吐量,提高系统性能。闫军等[6]使用多色集合理论得到仓库中货位的最优分区。分析发现,以上研究对于最小存储单元,如自动化立体仓库中托盘上货物的摆放规则,或AutoStore中不同料箱内货物的摆放规则并没有研究。所做内容均为在某一存储策略下讨论系统结构设计或系统运行时间,且未比较各存储策略之间的优劣,综合权衡系统效率和存储空间。
为解决上述问题,Gharehgozli等[7]首次在集装箱自动化堆场系统(Container Stack System, CSS)中提出了针对最小存储单元存储规则的指定存储与共同存储策略的概念。随后,Zaerpour等[8]在3DAS/RS系统中研究了指定存储与共同存储策略,以最小化系统作业时间为目标建立模型。Fumi等[9]提出了一种在指定存储策略下减少所需仓储空间的方法。Felix等[10]针对Kiva系统提出了一种最短路径的存储方法,通过实验证明,最短路径存储方法得出的结果优于基于规则的简单分配存储方法的结果。Singbal等[11]针对AS/RS系统,设计了3种基于周转频率的存储策略,将产品分配到对应通道,得到结论:3种存储策略在不同评价标准下,基于类的存储分配策略的性能优于基于周转频率的存储策略的性能。目前,针对AutoStore系统,Beckschäfer等[12]提出了一种离散事件模拟方法,讨论指定存储和每个料箱内存放2种商品的共同存储策略,结果表明,除非挖掘出产品一起订购的可能性,否则分法不会显著提高效率,选择合适的商品投入策略可以提高拣选效率达到5%。Zou等[13]同样研究了指定存储与共同存储策略,结果表明,指定存储比共同存储的系统订单处理时间提高了约24%,但多出约52%的储位面积,约50%的系统成本,且在指定存储策略下,系统的充填率较低,空间浪费严重。随着企业产品数量和规模的增加,企业不得不设置更多的存储空间,花费更多的存储成本,因此对于经营品类繁多或仓储空间有限的企业,更愿意选择共同存储策略。
文中在过往AutoStore研究的基础上,针对共同存储策略(每个料箱中存放的货物种类数大于1,每个堆栈中存放多种货物)订单吞吐时间长的问题,提出AutoStore系统货物的合箱方法。以机器人拣货过程中行走总距离最短为目标函数,建立基于货物关联规则的合箱模型,设计料箱的分配规则以减少翻箱时间,提出一种基于Apriori关联规则挖掘算法与混沌种子优化算法联动决策的混合优化算法。
1 问题描述和数学建模
1.1 问题描述及相关假设
AutoStore系统中货物的存储方式分为指定存储和共同存储,货物合箱是在应用共同存储策略的情况下,设计货物存放规则和料箱分配规则,使双指令任务下机器人拣选行走时间、翻箱时间最小化,作业效率最大化。在AutoStore系统中,订单处理的工作流程见图1,具体过程如下。
1)系统接收客户订单,为其分配处在空闲状态的机器人,机器人接收订单指令后从待位点行走至目标料箱处,若料箱不位于货架顶层,则机器人进行翻箱操作。
2)机器人携带目标料箱送至距离最近的工作站,由拣选人员从中选取需要的商品。
3)工作站操作完成交换料箱,机器人携带存储料箱到指定存储位置,并在该处停留。

图1 AutoStore系统顶层作业流程

为不失一般性,在建立数学模型时进行如下假设。
1)机器人翻箱操作时,四周堆栈未达到最大堆叠高度。
2)机器人采用专用机器人服务规则,一个工作站分配一个固定的机器人。
3)每个料箱有固定尺寸标准,料箱中容纳的所有货物的质量和体积不能超过限定值。
4)忽略机器人行走过程中的转向时间对优化结果的影响。
1.2 数学建模
在建立模型之前需明确翻箱操作,并将系统布局进行数学化表达。
1.2.1 机器人翻箱操作


图2 机器人翻箱示意图



式中:为阻挡料箱的数量;为单元料箱的高度;为单元料箱的宽度。
1.2.2 系统布局


式中:为工作站的数量;1、分别为系统的宽度和长度;为单元料箱的高度。
1.2.3 数学模型
在分析了上述相关问题后建立合箱模型,包括商品存放策略和料箱分配规则2个子模型。模型中使用的决策变量定义如下,其他参数变量定义见表1。
表1 模型中使用的参数变量

Tab.1 Parametric variables used in the model

条件:





文中的合箱模型是以使关联货物被分配到的料箱间的距离、顾客复购率最高货物到货架顶层距离,以及顾客复购率最高货物到工作站的水平距离之和的最小化为优化目标。约束条件(6)表示确保在分配过程中,每件货物只能被分配到一个货位,其中指待分配货物种类数;约束条件(7)表示由于系统中的每个料箱容量都有限制,且货物的存放不是紧密存储,因此设定料箱实际利用率为,已经分配货物的体积加上将要分配的货物体积,不能超过料箱容积与其实际利用率的乘积;约束条件(8)表示由于系统中的每个料箱都有最大载质量限制,因此待分配货物质量加上已分配货物质量之和不能超过料箱最大载质量;约束条件(9)表示待分配货物数量与其货物总数之间的比例应近似等于货物的需求频率(即货物支持度),这是因为若存储某种货物数量过高而需求频率较低,会造成浪费;反之,又会造成频繁补货。约束条件(10)表示已分配商品和待分配商品之间的距离用曼哈顿距离计算。
为满足模型中将需求频率大的货物优先放在距网格货架顶层最近,且距工作站最近的地方的要求,文中的第2个工作是设计料箱的分配规则,将需求频率从高到低货物的放置顺序与料箱的分配顺序一一对应。具体分配规则:不同层之间由上至下,先分配距离网格顶部最近的层,同层之间按照距离工作站的远近对称分配。图3中绘制了AutoStore标准布局的四分之一,根据式(4)确定工作站的位置。数字1—35即为同层间料箱的分配顺序。图3中相同颜色的格子代表到工作站单位距离相同的料箱,相同颜色内料箱的分配顺序又与料箱的单位宽度与长度有关。如分配顺序为2、3、4的3个料箱到工作站均为2个单位距离,其中2号料箱为沿宽度方向2个单位长度,3和4料箱为沿长度方向、沿宽度方向1个单位长度,而AutoStore系统中料箱的长度为649 mm、宽度为449 mm,因此优先分配2号料箱,其余层按照同样方法。这样的分配方式保证了高需求货物(高周转率料箱)集中在货架顶部且靠近工作站处,减少机器人翻箱的工作量;同时,以工作站所在行对称分布的方式,减少了翻箱过程中可能造成的拥堵和干涉,分散仓储区域的局部作业热度,减少了机器人的等待时间。
将上述料箱分配规则转化为料箱的分配优先度,设任意一个料箱的坐标为(b,b,b),则同层内料箱的分配优先度可由式(11)计算。b、b的绝对值越大,表示料箱距离工作站的单位距离越大,分配优先度越小;当单位距离相同时,b方向数值越大,到工作站的距离越长,分配优先度越小。按照料箱的分配优先度从大至小进行货位分配。
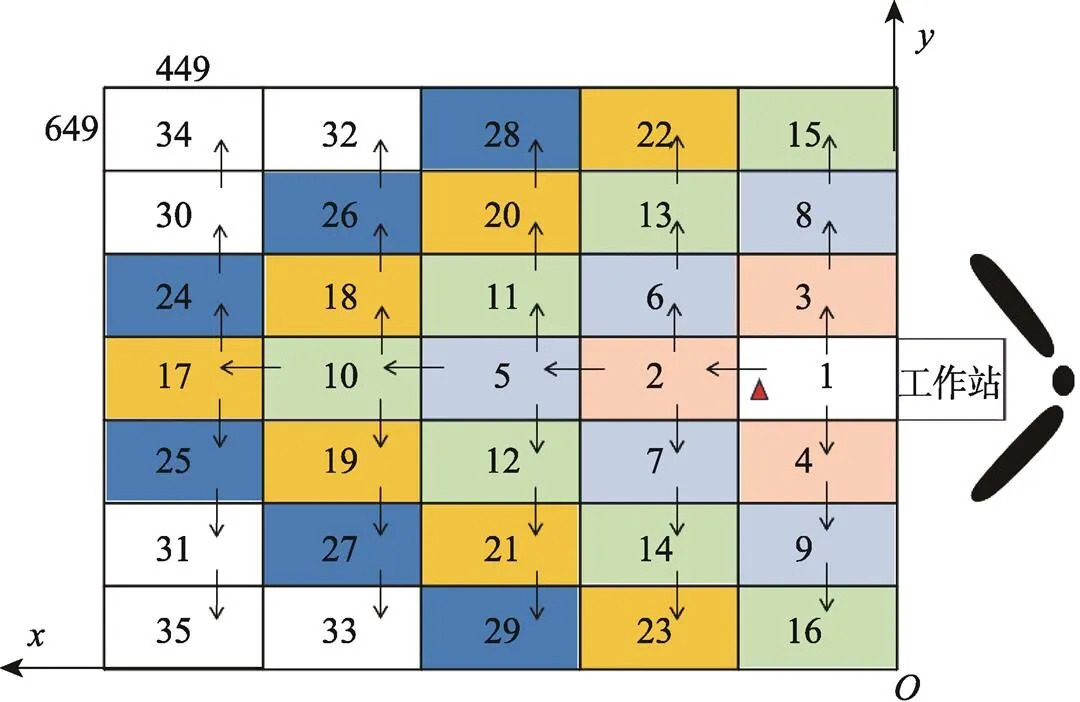
图3 最顶层料箱分配顺序

2 算法设计
文中算法是基于Apriori关联规则挖掘算法与混沌种子优化算法联动决策的混合优化算法(Apriori Chaotic Bean Optimization Algorithm, ACBOA)的求解合箱模型。文中算法的设计分为2个阶段,首先利用Apriori关联规则挖掘算法挖掘历史订单数据,实现对货物间关联规则的挖掘,其次将Apriori算法的结果输入混沌种子优化算法中;求解货物的合箱结果。
2.1 混沌种子优化算法
种子算法是张晓明等[14]受自然界种子传播方式的启发,提出的一种进化算法,他通过仿真实验证明了该算法较粒子群算法(PSO)具有较好寻优性能,并通过数学计算和测试函数证明了其能够以概率1收敛于全局最优解。基本种子优化算法的初始化过程随机,个体质量无法得到保证,容易陷入局部最优。混沌理论近年来被广泛研究,认为其可以加快算法收敛速度、提高求解精度,因此,文中针对基本种子算法存在的容易陷入局部最优、寻优精度低等问题,设计混沌种子优化算法,在基本种子算法的迭代中加入混沌序列,产生多个区域的局部最优解点,帮助种子避开局部极小值,快速找到最优解。
2.2 种子个体编码
对于货物分配问题,其解的结构包括起点||(可理解为待分配的货物)和终点||(可理解为料箱),这样可以得到一个||行||列的分配矩阵。为了能够确定唯一的分配矩阵,需要确定优先满足哪一个终点,以及确定优先由哪一个起点满足该终点。由于文中已经设计了料箱的分配顺序,因此将文中终点的优先级作为已知,采用直接编码的方式,将种子个体位置的维度设置为待分配货物的数量,每一维位置向量都代表一个货物,且各向量的分量不重复。设种子个体的向量=(1,2,…,x, …,x,…,x),则1→2→…→x表示分配到同一料箱中的商品为1,2,…,,其中x, x=1,2,…,且x≠x(≠)。
2.3 适应度函数及解码

根据合箱模型的约束条件,解码执行步骤如下。
1)参数初始化。设置最大迭代次数、种群大小和父种间的距离阈值。



3)计算每个种子的适应度值,找到适应值最优的种子,将其选为候选父代。
4)选择一个适应度值最优的种子作为1号父代种子,从剩余的种子中选择具有最优适应值的种子,并判断它与所选择的父代之间的近似程度(文中使用Apriori算法产生的结果)。
5)根据种群分布(文中为料箱的位置、质量和体积约束),在每个父代的扩散范围内生成相应的后代种子组。



7)判断是否满足终止条件,如果满足,结束算法;否则,执行步骤3。
8)输出结果,结束算法。
图4为ACBOA的具体算法流程,其中前8步为Apriori算法的步骤,第9到18步为混沌种子优化算法(CBOA)的步骤。
3 仿真实验
3.1 算例数据及算法参数设置


图4 ACBOA算法流程
3.2 仿真结果分析
以系统处理500、1 000、3 000张3种不同规模的订单数量为例进行分析。其中3 000张订单的处理结果:3 000张订单共包含28 722条商品购买数据,15 000种不同种类的商品,品类涵盖食品、药品、个护和运动等4个方面,共挖掘出货物关联规则126条,见表2。求得货物的合箱结果见表3。
为验证算法有效性,将混沌种子优化算法(CBOA)与基本种子优化算法(BOA)、粒子群算法(PSO)(此处默认已使用Apriori算法挖掘出货物的关联规则)在不同作业规模下运行50次的结果进行对比,见表4。适应度、收敛代数、收敛时间的箱线图比较见图5。设置连续迭代500次最优值不变为收敛的判断条件,根据文献[15],粒子群算法求解离散问题的参数设置:群体规模为20,惯性权重因子为1.0,学习因子为2,微粒最小位置值为0,最大位置值为4,微粒最小速度值为−4 m/s,最大速度值为4 m/s,进化次数为500,种群规模为100。
表2 货物关联规则(部分)

Tab.2 Goods association rules (partial)
表3 合箱结果(部分)

Tab.3 Consolidation result (partial)
注:数值表示货物编号。
表4 算法benchmark性能比较

Tab.4 Algorithm benchmark performance comparison

图5 算法优化性能箱线图比较
由图5可知,CBOA的数据波动明显小于PSO和BOA,说明CBOA稳定性强。CBOA的收敛时间和速度明显优于PSO,与BOA结果接近,这是因为基本种子算法更易陷入局部最优,从而更快收敛。算法求得的适应度值明显优于其他2种算法。
粒子群算法、基本种子优化算法和混沌种子优化算法这3种算法对合箱问题在3种作业规模下的算法收敛效果见图6。
分析图6中的收敛曲线和数据可以看出,粒子群算法收敛速度较慢,所求结果较基本种子优化算法和混沌种子优化算法相比较差;基本种子优化算法收敛速度很快,但是由于初始化过程随机,容易陷入局部最优,无法使种群集中在最优值附近;而文中提出的混沌种子优化算法,在种子迭代中加入混沌序列,产生多个区域的局部最优解点,帮助种子避开局部极小值,不仅避免算法过早收敛陷入局部最优,而且算法求解精度高。
将按照网格分区原则划分的随机存储和分区存储与按照货物最小存储单元划分的制定存储和共同存储两两组合,得到4种常见存储策略:共同分区存储、共同随机存储、指定分区存储和指定随机存储。分区存储是基于商品的订购频率进行分类分区,周转率前15%的商品归为A类,中间35%的商品归为B类,剩下50%的商品归为C类,A类商品存放在最靠近工作站处,B类次之,C类最远。将合箱存储的仿真结果与这4种存储方式进行对比,共设置订单平均处理时间变化率、机器人行走总时间变化率、机器人翻箱总时间变化率、平均每个订单需要搬运的料箱数变化率等4个实验评价指标,合箱存储相较于另外4种存储方式的变化百分比见表5。
由于指定存储策略下机器人没有翻箱时间,因此共同存储的机器人行走总时间和翻箱总时间不与指定存储比较。分析发现,相较于共同存储策略下的分区和随机存储,合箱存储在4个实验评价指标的数值均有所下降,因此说明合箱存储策略能够有效降低共同存储策略下系统订单吞吐时间。合箱存储比指定随机存储的订单处理时间短8.5%,比指定分区存储的时间长19.92%。文献[12]中提到,共同存储与指定存储下系统订单处理时间相差约24%,而在文中所得出的结果中,共同存储策略下的合箱存储与指定分区存储的时间差缩小到19.92%。综上,合箱问题的提出能够缩小共同存储与指定存储订单处理时间的差距,进一步缩短共同存储策略的订单处理时间,为经营品类繁多或仓储空间有限的企业提供选择。

图6 不同作业规模下算法收敛效果
表5 合箱存储相较于另外4种存储方式改进值

Tab.5 Improved value of consolidated storage compared to the other four storage methods
4 结语
共同存储策略与指定存储策略相比,具有系统成本低、吞吐时间长等特点,考虑如何缩短系统的吞吐时间,平衡系统订单处理能力与运行成本,为经营品类繁多但仓储面积有限的企业提供更适合的存储策略。通过分析共同存储策略存在机器人翻箱动作、箱内货物摆放杂乱导致系统订单处理时间长的问题,结合AutoStore系统的工作原理,在订单处理过程中,建立以机器人行走距离最短为目标函数的合箱模型,设计了不同层之间由上至下,同层之间按照距离工作站远近进行先后分配的料箱分配规则,采用基于Apriori算法与混沌种子优化算法的复合优化算法进行求解。仿真结果表明,文中提出的混沌种子优化算法比粒子群算法和基本种子优化算法的运算速度更快、优化效率更高。文中提出的货物合箱方法为紧致化仓储系统提供了一种新的货物存储方式,广泛适用于电商、医药等经营品类繁多,但仓储面积有限的企业,未来会进一步探讨不同机器人服务规则和订单分批策略对货物合箱的影响。
[1] Swisslog. 瑞仕格AutoStore落户上海为智慧用水打造物流之枢[J]. 现代制造, 2021(11): 40-41.
Swisslog. Swisslog AutoStore Settled in Shanghai to Create a Hub for Smart Water Logistics[J]. Maschinen Markt, 2021(11): 40-41.
[2] 朱杰, 周丽, 郭键. 分类存储人工拣选随机服务系统效率研究[J]. 管理科学学报, 2012, 15(2): 59-71.
ZHU Jie, ZHOU Li, GUO Jian. Research on Random Service System Efficiency of Sorted Storage Manual Order Picking Manners[J]. Journal of Management Sciences in China, 2012, 15(2): 59-71.
[3] BALLESTÍN F, PÉREZ Á, QUINTANILLA S. A Multistage Heuristic for Storage and Retrieval Problems in a Warehouse with Random Storage[J]. International Transactions in Operational Research, 2020, 27(3): 1699-1728.
[4] 刘恺文, 曹政才. 基于改进灰狼优化算法的自动化立体仓库作业能量优化调度[J]. 计算机集成制造系统, 2020, 26(2): 376-383.
LIU Kai-wen, CAO Zheng-cai. Energy-Optimized Task Scheduling of Automated Warehouse Based on Improved Grey Wolf Optimizer[J]. Computer Integrated Manufacturing Systems, 2020, 26(2): 376-383.
[5] EDER M. Analytical Model to Estimate the Performance of Shuttle-Based Storage and Retrieval Systems with Class-Based Storage Policy[J]. The International Journal of Advanced Manufacturing Technology, 2020, 107: 1-16.
[6] 闫军, 王璐璐, 常乐. 多色集合在仓配一体化仓库货位分配建模中的应用[J]. 包装工程, 2019, 40(23): 203-208.
YAN Jun, WANG Lu-lu, CHANG Le. Application of Polychromatic Set in Cargo Space Allocation Modeling of Warehouse Integrated with Storage and Distribution[J]. Packaging Engineering, 2019, 40(23): 203-208.
[7] GHAREHGOZLI A H, YU Yu-gang, KOSTER R, et al. A Decision-Tree Stacking Heuristic Minimising the Expected Number of Reshuffles at a Container Terminal[J]. International Journal of Production Research, 2014, 52(9): 2592-2611.
[8] ZAERPOUR N, YU Yu-gang, KOSTER R B. Storing Fresh Produce for Fast Retrieval in an Automated Compact Cross-Dock System[J]. Production and Operations Management, 2015, 24(8): 1266-1284.
[9] FUMI A, SCARABOTTI L, SCHIRALDI M M. Minimizing Warehouse Space with a Dedicated Storage Policy[J]. International Journal of Engineering Business Management, 2013, 5: 1-10.
[10] WEIDINGER F, BOYSEN N, BRISKORN D. Storage Assignment with Rack-Moving Mobile Robots in KIVA Warehouses[J]. Transportation Science, 2018, 52(6): 1-10.
[11] SINGBAL V, ADIL G K. Designing an Automated Storage/Retrieval System with a Single Aisle-Mobile Crane under Three New Turnover Based Storage Policies[J]. International Journal of Computer Integrated Manufacturing, 2021, 34(2): 212-226.
[12] BECKSCHÄFER M, MALBERG S, TIERNEY K. Simulating Storage Policies for an Automated Grid-Based Warehouse System[C]// International Conference on Computational Logistics. Springer, Cham, 2017.
[13] ZOU B, KOSTER M, XU X. Evaluating Dedicated and Shared Storage Policies in Robot-Based Compact Storage and Retrieval Systems[J]. ERIM Report Series Reference, 2016: 132-146.
[14] 张晓明,王儒敬,宋良图.一种新的进化算法——种子优化算法[J].模式识别与人工智能,2008,21(05):677-681.
ZHANG Xiao-ming, WANG Ru-jing, SONG Liang-tu. A New Evolutionary Algorithm-Seed Optimization Algorithm [J]. Pattern Recognition and Artificial Intelligence,2008,21(05):677-681.
[15] 王凌, 刘波. 微粒群优化与调度算法[M]. 北京: 清华大学出版社, 2008: 1-219.
WANG Ling, LIU Bo. Particle swarm optimization and scheduling algorithms[M]. Beijing: Tsinghua University Press, 2008:1-129.
Cargo Consolidation Method in New Unmanned Warehouse AutoStore
YANG Wei, ZHANG Zi-han, ZHANG Xiao-nan, MA Wei
(School of Mechanical and Electrical Engineering, Shaanxi University of Science and Technology, Xi'an 710021, China)
The work aims to reduce the order processing time of the AutoStore system under the common storage strategy and solve the storage problem encountered by companies with a wide range of goods but limited storage area. A storage method of cargo consolidation was proposed, and a hybrid optimization algorithm of association rule mining algorithm and chaotic seed optimization algorithm was designed for solution. Then, the analysis was carried out from the three aspects of robot turning operation, bin distribution rules, and system layout. Combined with AutoStore operation rules, a mathematical model with the shortest walking distance of robot picking as the objective function was established to output the heat of the goods through the Apriori algorithm, and input the chaotic seed algorithm to get the storage allocation result, thus realizing the linkage decision-making. The chaotic sequence was added in the iteration of the basic seed algorithm to help the seed avoid local minima. The case analysis showed that the cargo consolidation method could significantly reduce the order processing time of the AutoStore system under common storage, and narrow the gap with the specified storage strategy order processing time. Compared with the particle swarm optimization algorithm and the basic seed optimization algorithm, the chaotic seed optimization algorithm had higher optimization efficiency and better stability. This research provides a more suitable cargo storage strategy for companies with a wide range of business categories but limited storage area, which has strong operability and practical significance.
AutoStore system; storage strategy; Apriori association rule mining algorithm; chaotic seed optimization algorithm
F274
A
1001-3563(2022)17-0174-10
10.19554/j.cnki.1001-3563.2022.17.022
2021−11−02
国家自然科学基金青年科学基金(71802120);西安市未央区项目(201939)
杨玮(1972—),女,博士,教授,主要研究方向为智能物流系统优化。
责任编辑:曾钰婵

