锥齿轮结构化网格生成方法与参数化建模仿真

冀林昊，买买提明·艾尼

(新疆大学机械工程学院，新疆乌鲁木齐 830000)

0 前言

锥齿轮是相交轴动力传递最重要的机械传动方式之一。 精准计算渐开线直齿锥齿轮的动力学性能，发掘内在规律，进行合理的设计，对提升传动的平稳性、提高齿轮的承载能力、避免共振发生、延长齿轮及系统整体工作寿命极为重要。 由于锥齿轮结构的复杂性，在进行设计与分析时,最大的难题即空间实体结构模型的建立问题。在进行仿真模拟时,采用的方法通常是先使用外部软件建立模型，导入工程仿真软件(如ANSYS)，然后进行网格划分、加载边界条件和分析选项设置等操作，最后求解。这种方法引发三大问题：(1)模型建立时，需要反复进行数据处理，工作量庞大、操作流程繁杂且可重复性差；(2)划分正确规整的结构化六面体网格难以实现，容易出现奇异单元、散杂四面体单元、展开线轮廓无法保证等，因此很多情况下习惯进行四面体网格划分，从而影响计算精度；(3)在设计中修改某个或几个几何参数，则必须重复类似过程，延伸建模设计和数值模拟时长，并且在模型导入时也可能会因数据通信和兼容性等问题出现错误，甚至导致无法进行后续的分析计算，致使重新建模。

基于此类问题，应找到一种锥齿轮齿廓的正确建模、六面体网格参数化划分方法与仿真技术，建立满足锥齿轮设计需求的建模方法和数值仿真平台。许多学者已在这方面开展了研究。靳天姣等运用APDL语言，将板片空间结构与网壳结构的建模程序相组合，实现同一程序两种结构的自动建模。在齿轮传动方面，于亚妮等用ANSYS对修形齿轮一个齿进行了有限元六面体网格划分。师彦龙等针对一对渐开线齿轮开发了四面体网格和建模参数化分析系统。

以上研究成果对齿轮参数化建模与分析带来了一定的方便，但是在直齿锥齿轮展开线廓线的正确网格划分和全齿轮参数化六面体网格划分与仿真分析方面还不完善。

本文作者利用APDL语言，结合Visual C++，以渐开线直齿锥齿轮为例，对锥齿轮的渐开线齿体部分和锥体部分进行分块处理，并在块体之间建立连接关系，然后进行六面体网格划分；通过扫掠方法生成规则的六面体网格单元，实现了锥齿轮的建模、六面体网格划分和动力学分析全过程的参数化，开发了满足渐开线直齿锥齿轮的建模、网格划分与数值分析的参数化软件平台。通过应用此平台，输入关键参数(如模数、齿数、单元尺寸等)，系统可自动迅速完成锥齿轮三维建模、规整六面体网格划分及荷载施加与边界条件设定，并通过选项自动进行动力学数值模拟与结果显示。

1 建模与网格划分参数化方法

1.1 锥齿轮主副参数与算法

本文作者根据渐开线函数和齿根过渡曲线方程，确定直齿锥齿轮的关键参数，将齿数、端面模数、端面压力角、顶隙系数、齿顶高系数、分锥角等设定为主驱动参数；将任意圆齿高、齿顶圆直径、基圆直径、齿根圆直径、渐开线任意圆直径、分度圆直径、内孔直径、锥距、齿根角、顶锥角、根锥角、齿宽、齿根倒圆半径设定为副驱动参数；将上下端面与横轴的距离设定为位置关系参数。通过确立齿轮尺寸主副驱动参数之间的关系式，建立直齿锥齿轮的底层算法。在划分六面体网格时，为了始终保证单元节点正确落在展开线齿廓的轮廓上，依据表1中的主副驱动参数关系式和渐开线函数方程(如式(1)所示)，进行坐标变换推导出渐开线上任一点在直角坐标系中的坐标(()，())与主副驱动参数之间的算法关系，如式(2)所示：

inv==tan-

(1)

(2)

式中符号含义见表1。

通过式(1)和(2)精准计算了落在轮齿齿廓展开线上的每个节点，并将其作为算法以参数化的方式编写APDL命令流。同时，通过表1和表2所示的齿轮主参数和副参数及相互关系式，编程实现锥齿轮的参数化建模。

表1 锥齿轮主副参数与参数之间的关系

表2 锥齿轮主参数

如果齿根圆大于基圆,齿根圆压力角计算方法为

=arccos()

(3)

齿根圆小于基圆的情况，取0。

1.2 齿廓线生成、分块化网格划分与合并

1.2.1 渐开线齿廓的生成

由于齿轮结构复杂、齿数多，齿轮三维实体的建模非常困难。首先，建立渐开线上任意一点在直角坐标系中的横纵坐标与主副驱动参数之间的算法关系。创建个插值点，并引用B样条曲线依次连接插值点生成若干段样条曲线，然后再用命令LCOMB依次连接几段样条线将其合并成一条完整的渐开线齿廓曲线。其次是将齿根处渐开线进行圆角处理形成齿根过渡曲线，最终建立完整的渐开线齿廓。基本方法与实现过程如图1所示。

图1 渐开线齿廓与对称半齿轮端面廓线生成

1.2.2 分块化网格划分

渐开线直齿锥齿轮几何形状是中心对称的。因此第一根轮齿模型网格划分后，通过环形阵列实现齿轮整体网格模型。所以，一根齿网格划分是最关键的一步。从端面来看可将一根齿分为渐开线齿体部分A和锥体部分B，因此可采取分块网格划分方法分别进行体网格划分。根据齿廓的复杂性，将一根齿分成易于生成规则六面体网格的两部分，如图2 (a)所示的A、B。然后分别在两个分块区采用映射方法直接划分规整的六面体网格到锥体和齿体上(如图2(b)、2(c)所示)；其次将两个块体进行合并，得到完整划分网格的一根轮齿模型(如图2(d)所示)；最后将划分网格的第一根齿进行旋转复制，生成整个锥齿轮的结构化六面体网格模型(如图2(e)所示)。

图2 分块化网格划分与旋转复制合并网格生成

对一根齿体分块化网格划分后，执行锥齿轮一根齿的齿体旋转复制操作时，在相邻单齿齿体分界面处分别产生一个包含重合的节点和关键点的重合面，实际是相互分离的两个面，必须对重合的节点和关键点进行合并，使分离的两部分连接成为一个整体，保证后续的计算无误。对于已经划分网格的区域，通过执行3次合并操作：第一次，合并重合节点，使其成为公共节点; 第二次，合并分离单元，使单元间共享信息；第三次，合并关键点和实体模型，使分离的两根齿体在重合面处通过共享的单元和节点连接为一体。顺序执行3次合并操作，使合并完成后不产生孤立节点，保证齿体之间连接处节点统一、不出现漏洞，使结构成为完整的一体。

2 系统总体架构设计与实现

2.1 架构设计与算法流程

根据有限元分析的基本过程，锥齿轮参数化建模与数值分析软件主要包含参数交互界面、建模与计算、结果显示三大部分，并利用C++与APDL联合编程方法对软件系统进行详细的模块化架构设计，如图3所示。其中，图3(a)为锥齿轮参数化建模及其数值分析软件系统的算法流程，同时表达了系统开发的基本过程；图3(b)为软件系统的架构设计框图。

图3 算法流程与架构设计

2.2 用户交互与调用

2.2.1 接口程序

根据设计需求在用户窗口界面输入参数，软件平台通过接口程序，使外部进程后台调用ANSYS Batch，自动完成参数传递与程序导入，实现建模与分析需求。以下是接口程序:

rootansys=root;

this->ansysProcess->StartInfo->FileName = root;

ansysProcess->StartInfo->FileName = root;

this->ansysProcess->StartInfo->Arguments="-b-p ane3fl -i code.in -o Info. out";

this->ansysProcess->StartInfo->WindowStyl=System::Diagnostics::ProcessWindowStyle::Hidden;

其中: b表示采用ANSYS Batch模式; p 表示指定license；ane3fl表示采用ANSYS Multiphysics; i表示输入文件为code.in; o表示输出文件为Info. out。

2.2.2 参数输入界面与可视化

采用Visual C++对ANSYS进行二次开发，封装完整有效的APDL命令流，并通过简单易用的Winform窗体程序，开发友好的用户界面，以利于参数的交互输入，实现建模与分析全过程的参数化。图4所示为作者开发的软件平台。

图4 软件平台

2.3 用户界面的传参与接收

正确实现直齿锥齿轮六面体网格划分与参数化建模仿真必须将用户值通过程序、根据函数方法全部传递到APDL命令流对应的变量中；然后通过接口程序使参数化建模与仿真软件平台自动调用ANSYS Batch模式，再通过输入输出功能将包含用户信息的APDL命令流自动写入后缀为. bat类型的文件中；最后，ANSYS自动读取该文件内信息，实现模型的建立与数值仿真分析等功能。由于程序量较多，对涉及传参的全部代码不做详尽的解读也不过多赘述。用户界面参数传递与接收的部分程序如下:

this->code->fileStart( false ) ;

this->code->fileStart(false);

this->code->ModelFourLoadsCode(this->textBox1->Text,this->textBox2->Text);

this->code->fileEnd();

void Model(String^z,String^m)file->

WriteLine("z="+Convert::ToString(z),"m=

"+Convert::ToString(m)) ;

3 参数化分析平台及其建模速度

3.1 参数化模态分析

采用本文作者引入的循环对称方法所开发的锥齿轮六面体网格划分与参数化建模仿真软件对某型采棉机动力系统中的锥齿轮零件进行快速建模与模态分析，获取该齿轮的动态特性。

齿轮规格见表3， 锥齿轮参数化建模与网格划分模型见图5。表4为齿轮模态分析各阶模态频率，图6为参数化平台求解的锥齿轮模态振型。齿轮传动核算实例所用材料参数规格为: 弹性模量2.1×10Pa、泊松比0.277、密度7.78×10kg/m。

表3 齿轮规格

图5 锥齿轮参数化建模与网格划分模型

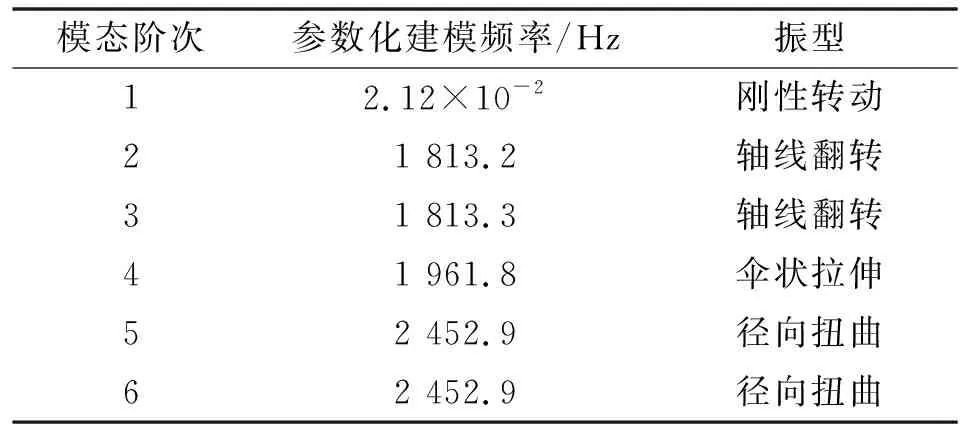
表4 模态分析各阶频率

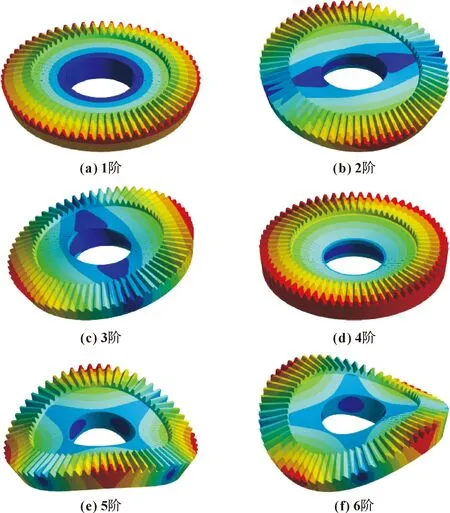
图6 参数化平台求解模态振型图

通过文中提出的结构化六面体网格划分方法和参数化模态分析软件平台对锥齿轮进行动力学分析，计算前6阶模态频率，可以清晰地看出各阶模态在不同激振频率下的振动形式和形变趋势，求出锥齿轮的固有频率和共振发生的激励频率，为后续研究动态响应、降低系统振动、减小啮合冲击提供参考，为齿轮系统设计提供指导。

3.2 建模速度对比

为说明锥齿轮参数化建模与网格划分程序的优势，将本文作者开发的参数化平台的建模和网格划分速度分别与UG和有限元软件ANSYS Workbench进行对比，结果见表5。可以看出：在锥齿轮的建模与网格划分速度方面，参数化方法比传统的CAD建模和Workbench有显著速度优势，且建模速度提升了91.3%，网格划分速度提升了81.2%。根据对比算例结果可知本文作者开发的参数化仿真平台不仅保证了锥齿轮模型渐开线的准确性，更是在速度上取得显著成效。该系统可应用于齿轮传动系统的计算力学、强度、振动和可靠性分析，并为后续的多学科优化设计奠定基础。

表5 锥齿轮建模速度对比

4 结语

该平台通过使用锥齿轮的主副驱动参数的关系式，建立参数化建模的底层算法。利用C++语言编程实现了六面体网格划分和参数化分析平台前处理和后处理，显著改善了锥齿轮六面体的网格划分质量、建模和分析速度。

根据渐开线直齿锥齿轮的结构特点，通过坐标变换，提出渐开线齿廓结构精确建模和六面体网格参数化划分方法，并实现参数化程序编制。

利用此参数化软件平台计算得到锥齿轮前6阶模态频率，提高了渐开线直齿锥齿轮的建模效率和网格划分速度，同时将锥齿轮的建模时间缩至7.2 s之内。建模效率提升91%以上，网格划分速度提升81%以上，显著降低建模、划分网格、分析时长，使研发成本下降、设计周期缩短。