基于流固耦合的脱硫搅拌器振动特性分析

蒋麒麟，但斌斌，龚昌运，王伟，刘洋，都李平

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北武汉 430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北武汉 430081；3.武汉钢铁有限公司技术中心，湖北武汉 430080)

0 前言

现代工业中使用的特种钢由于其恶劣的服役环境，对钢中的硫含量要求更严格，需要低于0.005%。铁水脱硫过程是指转炉冶炼前的铁水预处理工艺。其中，KR脱硫由于其优良的动态条件和高脱硫率，在提高钢材性能、保证连铸和钢坯质量、降低预处理成本等方面具有明显优势。铁水脱硫搅拌器是实施KR脱硫的重要设备。关于KR脱硫搅拌器，刘鹏、李文明、毕学工、肖林伟等都进行了相关研究。刘鹏应用Fluent软件，结合多重参照系方法，采用Eulerian多流体模型和标准-湍流模型，研究了KR机械搅拌脱硫混合器中流体的流动特性。李文明应用数值方法研究了KR机械搅拌和喷吹搅拌的动力学特性，分析了KR机械搅拌流场和铁水罐内自由液面凹进深度的变化规律以及喷吹搅拌时气泡对流场的影响。毕学工等通过建立不同工况下的混合模型，利用软件Fluent仿真得到影响混合效果的最佳工况。肖林伟等通过模拟搅拌器的中后期状态，根据脱硫剂的运动和分布，分析出搅拌器中后期所需的转速。

上述研究人员主要研究了搅拌器对脱硫和搅拌的影响，但忽略了KR脱硫搅拌器在脱硫过程中的振动问题，没有分析搅拌器自身在脱硫过程中的振动特性。本文作者利用有限元软件对基于流固耦合的脱硫搅拌器振动特性进行数值模拟，旨在为搅拌器结构的设计和优化提供参考。

1 搅拌器数学模型的建立及求解

1.1 流场控制方程

在实际生产过程中，铁水在罐内的流动非常复杂，为方便研究，对模型做以下简化和假设：(1)罐内铁水的黏度恒定；(2)忽略温度场和浓度场对铁水物性参数的影响；(3)考虑重力加速度沿轴向下，大小为9.8 m/s。

在非定常条件下，罐内铁水的基本方程包括质量控制方程与动量控制方程。

质量控制方程(连续方程)：

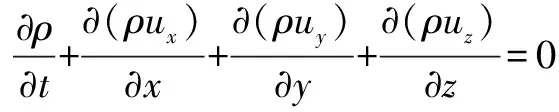
(1)

式中：第2、3、4项为质量流密度的散度，表示单位时间内通过单位面积的流体质量；为流体密度，kg/m；为时间，s；为流场速度，m/s；、、分别为速度矢量在、、方向的分量。

动量控制方程：

(2)

式中：为压力，Pa；为应力张量；为包含其他与模型相关源项，如自定义源项。

1.2 流固耦合方程

流体与固体模型的网格单元类型可以不同，但在耦合面上必须满足应力、位移、热流量和温度等变量守恒，即满足以下4个方程:

=

(3)

=

(4)

=

(5)

=

(6)

式中：、分别为流体与固体在耦合面上的位移，m；、分别为流体与固体在耦合面上的剪切应力，Pa；、分别为流体和固体在耦合面上的热流量，W；、分别为流体和固体在耦合面上的温度，℃。当不考虑温度变化时，应同时满足位移平衡方程和应力平衡方程，即通过满足这两个变量的守恒实现流体与固体之间分析参数的传递。

2 搅拌器仿真模型

2.1 搅拌器三维模型的建立

根据我国某钢厂KR脱硫工艺，结合水模型试验中的分析方法，应用相似原理，按1∶6建立铁水罐和搅拌器的数值模型。搅拌器和铁水罐所用材料为Q235，密度7 850 kg/m，弹性模量206 GPa，泊松比0.3，质量4 522 kg。

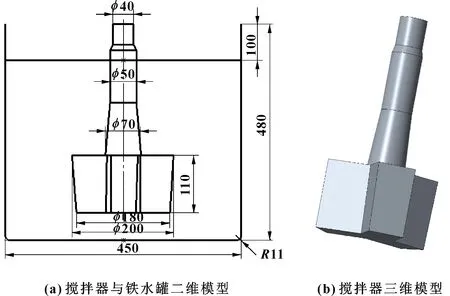
图1 搅拌器模型

2.2 边界条件及计算

Gambit软件作为Fluent的前处理器被广泛地用于数值模拟网格划分，将三维软件中建立好的三叶常规搅拌器三维模型导入Gambit中进行前处理网格划分，并在Gambit中将它划分为3个区域：动区域、静区域和空气区。其中，动区域存在斜边和倒角，几何形状不规则，使用结构四面体网格，采用Tet/Hybrid网格类型；静区域与空气区模型几何形状规则，使用结构六面体网格，采用Hex/Wedge网格类型，网格数目共348 469个。划分好的网格如图2所示。

图2 常规三叶模型网格

求解模式为有限体积法，流体流动为定常流动。图3所示为搅拌器边界条件设置，采用VOF模型模拟流场中的气液两相流，使用多重参考系法处理动区域与静区域的能量传输现象，两相交面设定为交界面(interface)，容器固体壁面为无滑移边界条件(no slip)。搅拌器叶片为运动壁面，动网格与搅拌器同步转动，转速为150 r/min；罐壁及下底面设置为(wall)；自由液面初始为静止状态，液面初始高度设定为380 mm，搅拌器潜入液面深度为300 mm。采用Simple算法对压力-速度耦合进行求解，离散格式采用一阶迎风，所有项的残差收敛范围均为1×10。时间步长设定为0.005 s，时间步设定为2 000步，共分析时长为10 s。

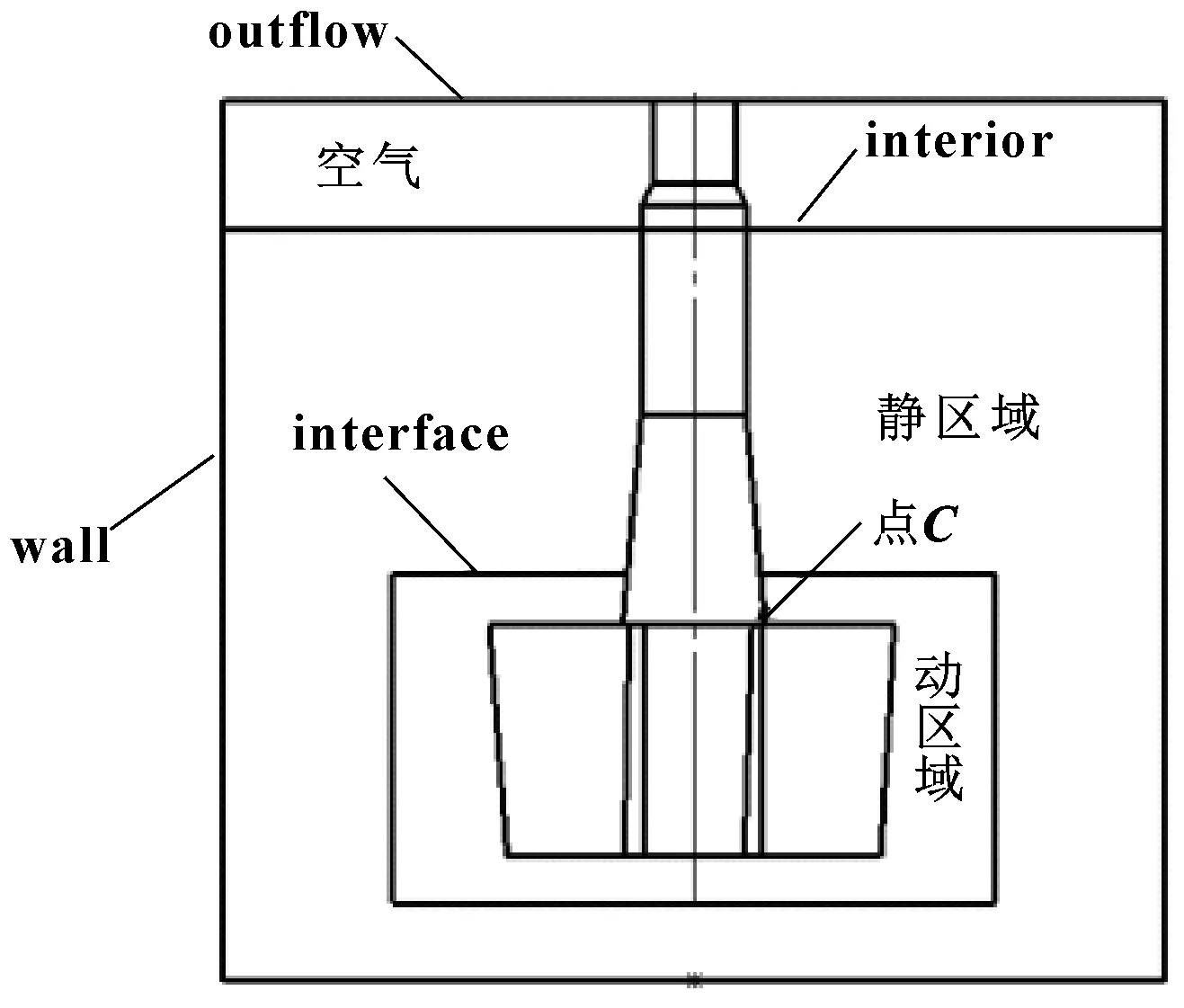
图3 搅拌器边界条件设置

3 仿真计算结果分析

3.1 流固耦合结果分析

由图4可以看出：搅拌器附近的区域流速较大，铁水罐壁及搅拌器上方区域流速较小。这是由于铁水罐内流体的速度来源于搅拌器的转动，搅拌器的转动带动动区域铁水作旋转运动，使得最先获得速度的是动区域附近的流体，该区域的流体最大流速为1.2 m/s。随着连续搅拌，动区域流体的动能向外扩散以传递能量，当到达铁水罐壁时，由于铁水罐壁的阻碍和吸附，使得在速度传递过程中损失了大量能量，在铁水罐壁处速度为0.1 m/s。由图5可以看出：搅拌头底部的流体压力较大，而搅拌轴附近的流体压力较小，底部最大流体压力约为1 350 Pa，搅拌轴附近最小流体压力为750 Pa。这是因为根据能量守恒原理在搅拌流场中的应用，流体速度大的区域压力较小，速度小的区域压力较大。在搅拌过程中，由于铁水罐底部流体速度小，底部附近的压力大，搅拌头动区域附近流体流速大，搅拌头动区域附近压力小。

图4 x截面速度分布

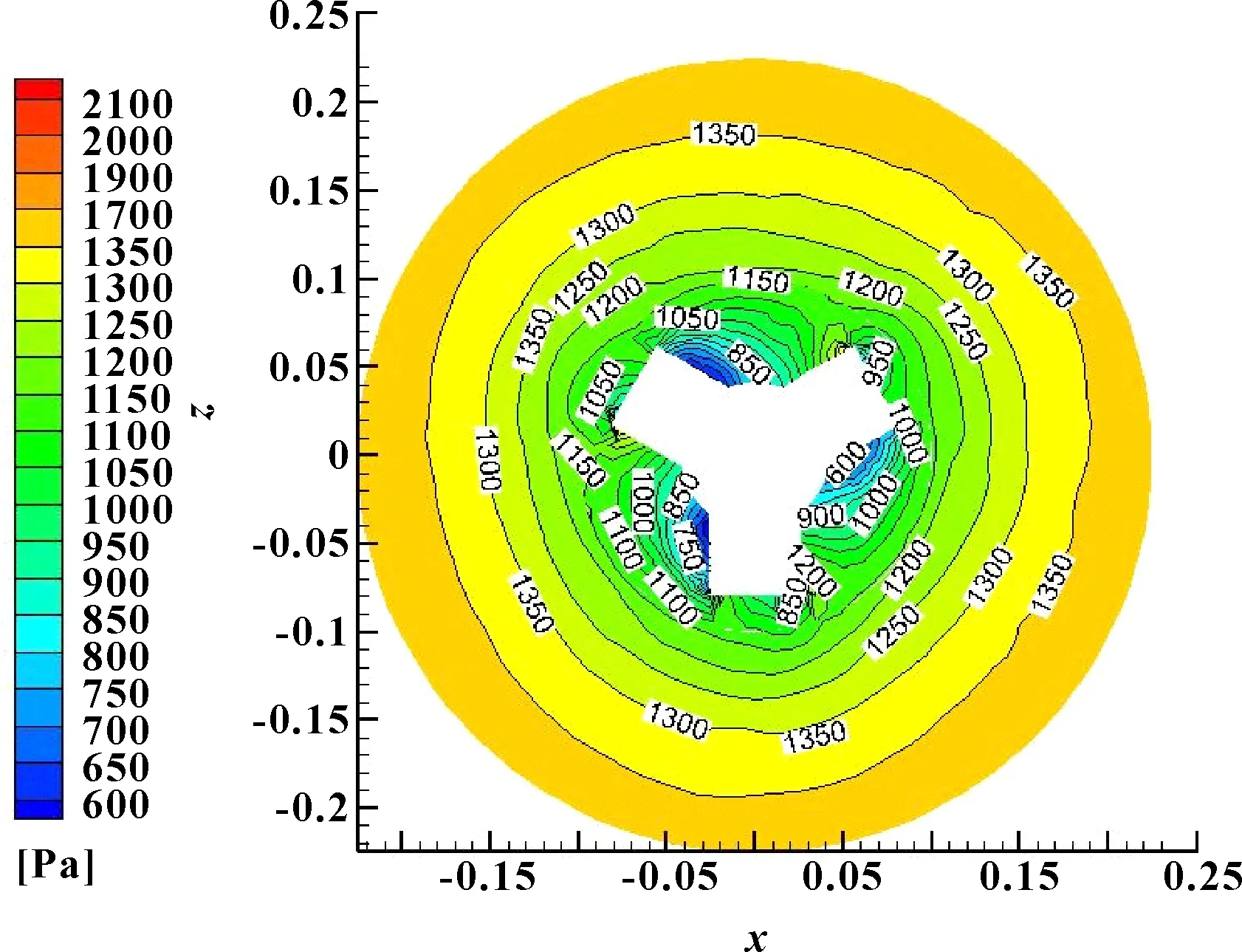
图5 x-y平面压力分布

由图6可以看出：搅拌器的最大变形发生在搅拌叶片底部区域，而最小变形发生搅拌器轴的上部。叶片底部区域压力大流速小，以至于变形量大，磨损严重。搅拌轴上部放置在空气中，没有流体与之接触，因此变形最小。由图7可知：最大等效应力发生在搅拌轴与搅拌叶片的连接处，数值为2 299.6 Pa，此处极易产生应力集中；最小等效应力出现在搅拌轴上部，数值为14.219 Pa，此处搅拌轴置于空气，不受流场的压力作用，所以该处的等效应力最小。

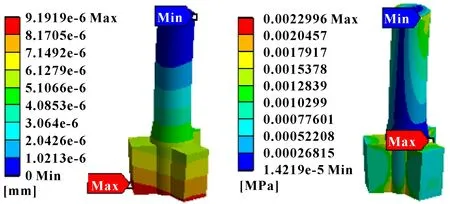
图6 搅拌器变形分布云图 图7 搅拌器应力分布云图

3.2 预应力模态分析

在结构振动中，低阶模态占主导地位，因此选择搅拌器的前4阶模态进行观测，结果如图8和表1所示。可以看出：在0～2 600 Hz频率范围内，最先发生变形的部位主要在搅拌器叶片处，该部位由于强大的流体压力而产生较大的变形。

由图8和表1可知：1阶模态的固有频率为253.19 Hz，其振型主要是搅拌器沿轴正向的弯曲变形，变形从搅拌器顶部至叶片底部逐渐增加，在叶片底部达到最大变形为12.689 mm；2阶模态的固有频率为901.62 Hz，其振型主要是搅拌器绕轴的扭转变形，搅拌器整体变形大，变形从搅拌器顶部至底部逐渐增大，在叶片端面处达到最大变形17.73 mm；3阶模态的固有频率为1 818.90 Hz，振型主要是搅拌器沿轴负向有明显的弯曲变形，由中间向两端变形逐渐减小；4阶模态的固有频率为2 552.10 Hz，振型主要是搅拌器以底端方向为中心轴线产生扭转变形，搅拌器叶片处达到最大变形9.661 7 mm。

图8 搅拌器前4阶模态振型

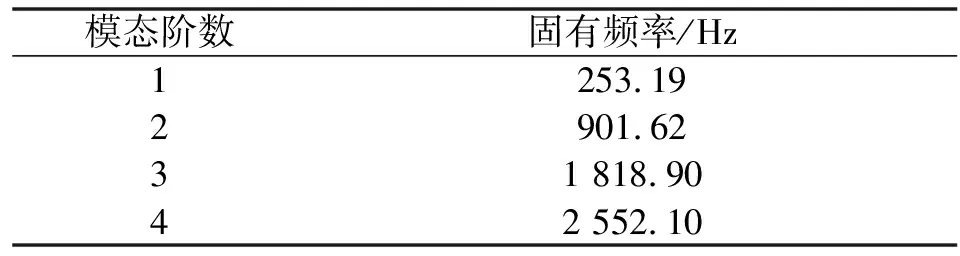
表1 搅拌器前4阶固有频率

3.3 搅拌器谐响应分析

搅拌过程中，搅拌器处于温度场、流场、力场等多物理场耦合作用的复杂服役环境下，会受到非定常压力场及不平衡的激励，从而引起不平衡响应。因此，通过谐响应分析来计算搅拌器的不平衡响应。

根据动平衡精度理论：

(7)

代入搅拌器设计参数：动平衡精度=2.5 mm/s，设计工作转速=150 r/min，系统总质量=4 522 kg，校正半径=208 mm，得搅拌器的最大剩余不平衡量为3 460.08 g。

偏心距为1.45 μm，搅拌器因质心偏心所产生的力为

=

(8)

式中：为不平衡质量；为转子的转速。

=cos

(9)

=sin

(10)

将这个力近似为2个相互垂直方向上的简谐力，两者之间的相位相差为90°。采用模态叠加法，选取搅拌器轴与叶片结合处点作为关键监测点，分析搅拌器的位移、加速度、应力和应变与激励频率之间的响应关系。

在模态分析得到的边界条件下，搅拌器激励频率求解范围设置为0～2 600 Hz，运算次数为260，即每次求解间隔10 Hz。在搅拌器点处2个垂直方向上添加简谐激振力，幅值为10 N、相位分别为0°和90°。通过对交汇点的振动谐响应分析，得到、、方向上位移、加速度、应力及应变与激励频率之间的响应曲线，如图9所示。

图9 振动特性响应曲线

由图9可知：激振力在搅拌器、、3个方向引起的响应趋势基本一致，随着激励频率的增加，交汇处点的位移、应力与应变都会在1阶(约260 Hz)和3阶(约1 800 Hz)固有频率附近出现峰值。由图9(a)可知：激励频率为260 Hz时，方向和方向的位移峰值分别达到0.001 6、0.000 3 mm;激励频率为1 800 Hz时，方向和方向的位移峰值分别达到0.006 3 mm和0.002 2 mm。由图9(b)可知：激励频率为1 800 Hz时，方向上的加速度峰值为8×10mm/s，方向上的加速度峰值为2.3×10mm/s。在搅拌器系统设计和结构优化中，可以在和方向上进行约束，以减小振动。由图9(c)(d)可知：由于存在、方向上的流体冲击，点位置处方向上应力响应最大、方向上的应变响应最大，激励频率为1 800 Hz时，方向上的应力达到9.5 MPa，方向上的应变达到1.5×10mm/mm。搅拌器轴和叶片结合处附近可以作为振动传感器安装位置，对搅拌器进行压力与速度的振动数据监测，以期为搅拌器结构设计与优化提供参考。

4 结论

本文作者采用单向流固耦合的方法研究了搅拌器的振动特性，通过分析数值结果发现：

(1)动区域附近的流体流速最大，数值为1.2 m/s，在混合罐的底部死区流速最小，数值为0.1 m/s；搅拌器底部的流体压力较大，而搅拌轴附近的流体压力较小；最大流体压力为1 350 Pa，最小流体压力为750 Pa；

(2)流固耦合作用下最大等效应力出现在搅拌轴与搅拌叶片连接处，数值为2 299.6 Pa；最小等效应力出现在搅拌轴上部置于空气部分，数值为14.219 Pa；

(3)通过研究交汇点的振动特性，发现由于内部流体的脉动，当搅拌器的激励频率为260 Hz时，和方向的位移峰值分别达到0.001 6、0.000 3 mm；当搅拌器的激励频率为1 800 Hz时，和方向的位移峰值分别达到0.006 3、0.002 2 mm，和方向的加速度峰值分别达到8×10、2.3×10mm/s。