随机载荷冲击下采掘机械截齿竞争失效可靠性分析

秦彦凯，张晓红，曾建潮，梁 好，石冠男

(1.太原科技大学 机械工程学院，山西 太原 030024；2.太原科技大学 工业与系统工程研究所，山西 太原 030024；3.中国煤炭科工集团 太原研究院有限公司，山西 太原 030006；4.太原科技大学 经济与管理学院，山西 太原 030024；5.中北大学 大数据与视觉计算研究所，山西 太原 030051)

大力发展采掘机械化是建设高产高效矿井的根本途径。截齿作为采掘机械的截割刀具，在截割过程中，直接与煤岩相互作用，其磨损程度直接决定了采掘机械的工作性能和使用寿命。据不完全统计，每万吨煤约消耗截齿1 300把，消耗资金高达520亿。在生产实践中，为保证作业连续性，提高生产效率，需储备大量截齿作为消耗备件，储备资金巨大。对截齿的磨损可靠性进行科学评价，是指导截齿最优更换储备、优化设计及采掘生产调度的重要依据之一。

国内外学者对截齿的磨损可靠性进行了较为广泛的研究。DEWANGAN等通过扫描电子显微镜和能量色散射线光谱对磨损图像进行分析，得到了截齿7种不同类型的磨损机制。LIU等通过研究截齿结构、尺寸等设计参数对截齿磨损的影响，分析了截齿的设计可靠性。ZHANG等通过研究等离子弧粉末堆焊对截齿磨损的影响，分析了截齿的加工可靠性。YANG等通过研究截齿旋转角、切削角等安装参数对截齿磨损的影响，分析了截齿的装配可靠性。SU等通过研究采掘机械截割速度、截割深度等使用参数对截齿磨损的影响，分析了截齿的使用可靠性。前期的研究通过考虑结构尺寸、制造工艺、安装位置、截割参数等影响截齿磨损的各种因素，从设计、加工、装配、使用等角度对其可靠性进行了分析。然而鲜有针对工况变化，对其运行可靠性进行的研究。在生产实践中，截齿的供应商通常会依据截齿的自然磨损特性给出建议的截齿管理标准，煤矿应用工程师再依据不同工况，结合生产经验，对相应的管理标准进行调整。因此，考虑不同工况的随机特性，建立冲击载荷影响下的截齿运行可靠性模型，对截齿更换和储备决策具有重要意义。

截齿的工况极其恶劣且复杂多变，截齿在截割过程中长期处于高应力和强冲击的状态。不同工况下煤岩的硬度不同，截齿承受的载荷不同，磨损的速率不同。通常，煤岩的硬度较低，其表面微凸起颗粒硬度低于截齿的材料硬度，此种情况下，截齿不断的受到煤岩的反作用，发生自然磨损退化；同时，煤岩中还夹杂着高硬度的矸石和断层，其表面微凸起颗粒硬度高于截齿的材料硬度，此种情况下，截齿不断的受到冲击性切削作用，发生加速磨损退化，而且由于矸石和断层体积与硬度的差异，加速磨损呈现出不同的持续时间和磨损速率；当矸石和断层的硬度达到一定程度时，截齿将会发生断裂、崩刃等瞬时致命性冲击失效。因此，磨损和冲击的共同作用是导致截齿失效的主要因素。

基于以上分析，将煤岩视为正常工作载荷，矸石和断层视为冲击载荷。由于矸石和断层的分布、硬度及体积均呈现随机特性，又称之为随机冲击载荷。正常工作载荷下的自然磨损退化和随机冲击载荷下的加速磨损退化的累积作用将导致截齿发生磨损性软失效，该失效形式种类占总失效形式种类的75%～90%。随机冲击载荷过大时将导致截齿发生冲击性硬失效，该失效形式占总失效形式的10%～25%。截齿失效表现为2类失效模式的竞争结果。

许多研究致力于金属材料磨损退化的建模。KANG等对模型驱动的退化方法进行了调查和综述，重点介绍了退化规律模型和随机过程模型。对于随机过程模型，提出了非单调和单调2种主要类型。由于磨损退化具有不可逆性，通常采用单调随机过程模型对其进行建模。如QIN等提出了一个基于逆高斯过程的退化模型来描述油气管道金属材料的磨损退化，并对其磨损可靠性进行了评估，促进了油气管道结构的完整性管理；ZHANG等提出了一个基于Gamma过程的退化模型来描述球面滚动轴承的磨损退化，并对其全寿命周期的磨损可靠性进行了评估。LI等提出了一个基于Gamma过程的退化模型来描述机床刀具的磨损退化，并对切削条件不变下的刀具磨损可靠性进行了评估，提出了不同情况下提高刀具可靠性的方法。田莹等提出了一个基于Gamma过程的退化模型来描述掘进机截齿的磨损退化，实现了对截齿磨损的剩余寿命预测。

根据不同的硬失效机制，前期对随机冲击的建模可以分为5类：① 当某个冲击量超过给定阈值时，系统的冲击为极值冲击；② 当相邻2次冲击的时间间隔小于给定的时间阈值时，系统的冲击为冲击；③ 当累积冲击量超过给定阈值时，系统的冲击为累积冲击；④ 当有个冲击量超过给定阈值时，系统的冲击为冲击；⑤ 当有连续的个冲击量超过给定阈值时，系统的冲击为运行冲击。此外，KONG等将复合绝缘子工作过程中的电晕放电定义为随机冲击，通过考虑电晕放电时间对复合绝缘子退化性能的影响，首次提出了一种考虑冲击持续时间的冲击退化模型，准确地反映了冲击持续时间对退化过程的影响。

在截齿截割煤岩过程中，矸石和断层作为最常见的载荷冲击，不仅具有随机的分布和硬度，而且具有随机的体积，因此，可将截割矸石和断层所需的时间定义为冲击持续时间，同时由于矸石和断层的硬度高于煤岩，故在不同的冲击持续时间内，截齿发生变速率加速退化。

近年来，考虑退化与随机冲击相关性的可靠性建模也得到了广泛的发展。HAO等建立了一个微机电系统竞争失效的可靠性模型，冲击会在其到达的瞬间造成退化量的突然增加；RAFIEE等建立了一个微机电系统竞争失效的可靠性模型，系统遭受冲击后会变得更脆弱，自然退化率会根据累计冲击量而发生变化。WANG等建立了一个微型发动机竞争失效的可靠性模型，系统遭受冲击后软失效阈值会根据冲击量而发生变化。

现阶段，尽管对退化和随机冲击之间的相关性进行了一定的研究，但鲜有研究同时考虑冲击到达、冲击幅值以及冲击持续时间对自然退化的影响，即随机载荷冲击不仅会在其到达的瞬间造成截齿的突然退化，而且会在不同的冲击持续时间内造成截齿的变速率加速退化，同时由于冲击持续时间的存在，相应地减少了自然退化时间。此外，为兼顾截齿的硬度和冲击韧性，在不同高度下截齿材料的硬度不同，通常顶部材料的硬度最大，而随着高度的降低，材料的硬度逐渐减小。在截割煤岩的过程中，随着磨损程度的增加，截齿的高度逐渐降低，其与煤岩接触材料的硬度也逐渐减小。而硬失效阈值本质上就代表截齿材料可承受的冲击强度，因此，截齿的硬失效阈值会随着磨损量的增大而降低，截齿抵御致命性冲击的能力逐渐减弱，对硬失效更加敏感。

综上，以上情况均符合截齿的应用实际，若简化这些过程，将导致对截齿可靠性评估的不准确。笔者通过考虑持续冲击、变速率加速退化和硬失效阈值变化对截齿磨损的影响，研究了随机载荷冲击下截齿竞争失效的可靠性建模问题。首先，详细描述了截齿软失效和硬失效的竞争失效模式，构建了截齿的冲击退化模型，以更好地反映截齿磨损退化与随机载荷冲击的相互影响。其次，在此基础上，构建了竞争失效模式下截齿的可靠性模型，以更好地反映磨损退化和随机载荷冲击对截齿退化过程的综合影响。最后，基于工程数据对截齿的可靠性模型进行了数值实验，并通过参数的灵敏度分析验证了该模型的有效性。

1 系统描述和退化建模

在考虑退化过程、冲击过程以及退化和冲击相关性的基础上，截齿竞争失效的基本原理如图1所示。一方面，在随机冲击的影响下，冲击会在其到达的瞬间造成退化量的突然增加，还会在不同的持续时间内造成变速率加速退化，同时由于冲击持续时间的引入，相应地缩短了自然退化时间，因此随机冲击影响下的退化过程包括长期连续的自然磨损退化、冲击引起的瞬时退化以及不同冲击持续时间内的变速率加速退化。当截齿高度低于软失效阈值时，截齿将发生如图2(a)所示的软失效。另一方面，随着退化量的逐渐增加，硬失效阈值逐渐降低，当冲击幅值超过硬失效阈值时，截齿将发生如图2(b)所示的硬失效。

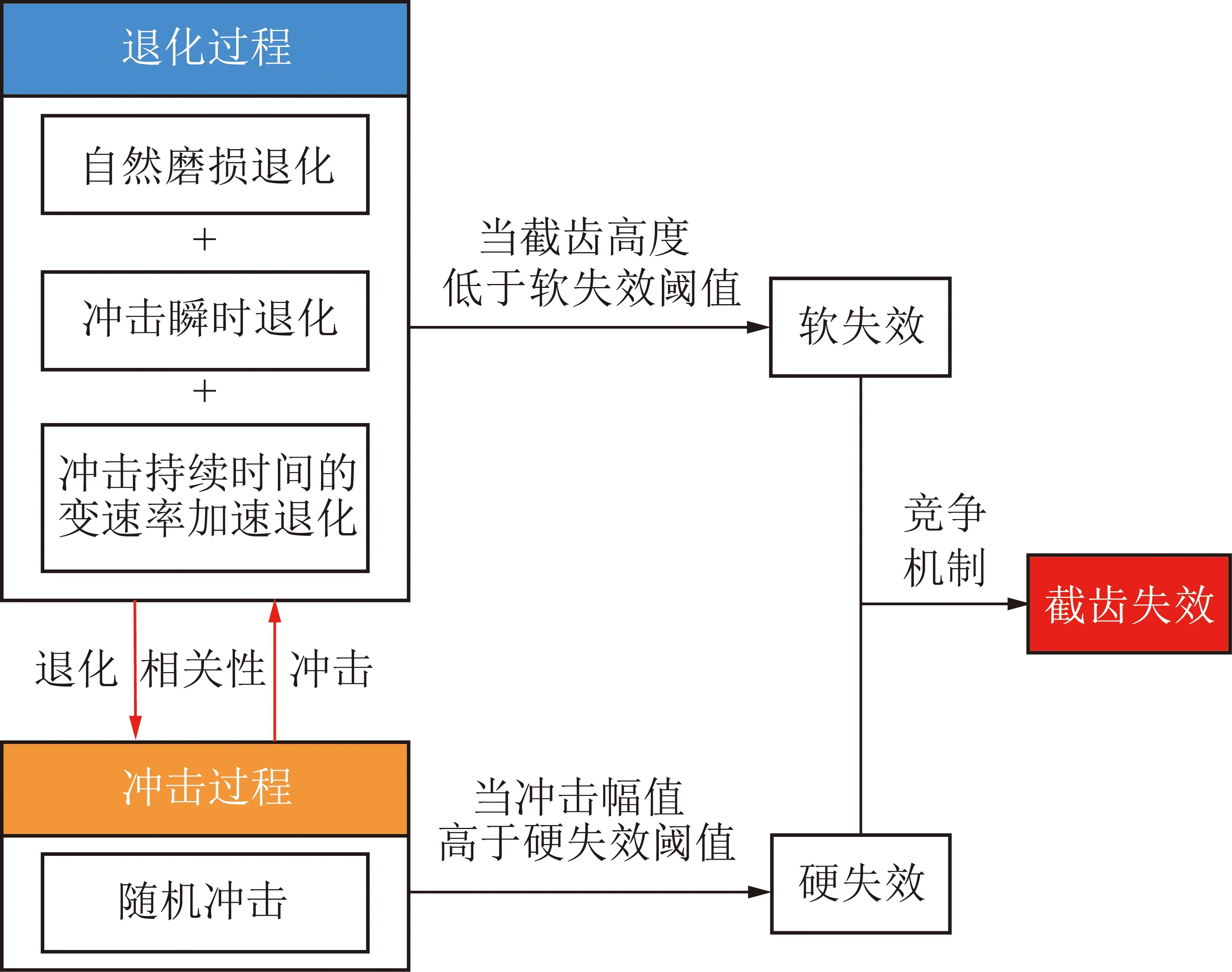
图1 截齿竞争性失效原理

图2 截齿失效形式

截齿竞争失效模式下的退化过程如图3所示。其中，为截齿的工作时刻；()为截齿在时刻的高度；为截齿的软失效阈值；()为冲击在时刻的幅值；为截齿的初始硬失效阈值；()为截齿在时刻的硬失效阈值；s为第次冲击的持续时间。基于相关领域的研究和相关学者的工程经验，可用退化规律模型来描述截齿的长期连续退化过程。由磨损导致截齿失效的主要评价指标为高度，且磨损时截齿高度的变化是一个逐渐减小的过程，故本文通过采用一个线性递减模型来描述截齿高度的变化，以直观地描述截齿的磨损退化过程，其表达式为

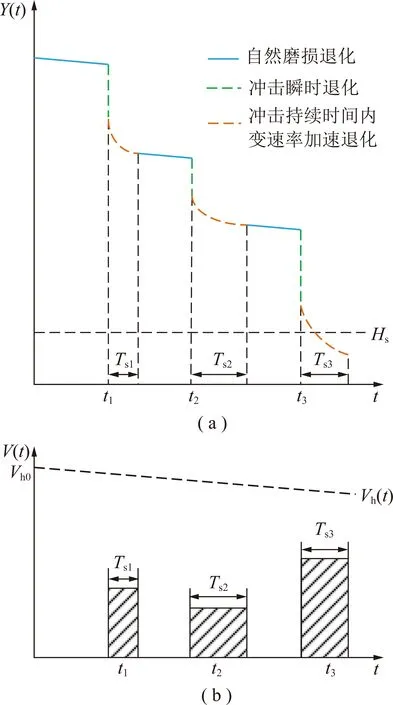
图3 竞争失效模式下截齿退化过程

()=(0)-()

(1)

式中，(0)为截齿的初始高度；()为截齿磨损的总退化量。

若在时刻之前，截齿遭受了次冲击，则总退化量()为自然磨损退化量()、冲击引起的瞬时退化量()和冲击持续时间内的加速退化量()之和，其表达式为

()=()+()+()

(2)

1.1 自然磨损退化建模

截齿的主要失效形式为磨损。不同的采掘机械具有不同的截割转速、截割扭矩、截割轨迹和截割滚筒形式，所用截齿也具有不同的外形结构、材料硬度、加工工艺和安装位置，以上各种因素的差异性均会对截齿磨损产生不同的影响，故难以用某一特定的公式来描述截齿磨损这一复杂问题。因此，考虑到截齿在自然磨损过程中的个体差异性，并且单位时间内的磨损增量为相互独立的非负值，可利用Gamma过程来描述截齿具有独立单调非负增量的连续自然磨损退化过程，故假设截齿磨损的自然退化率(单位时间的磨损量)服从Gamma分布，即～Gamma(,)，其中，≥0，为形状参数，为尺度参数，其概率密度函数()为

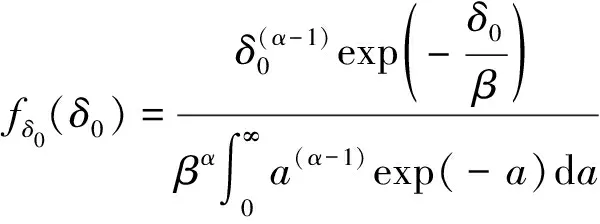
(3)

式中，为积分计算中的中间变量。

1.2 随机载荷冲击建模

煤田地质条件复杂多变，煤岩中无规律地存在着高硬度的矸石和断层，致使截齿在截割煤岩时会受到交变载荷的随机冲击。由于高硬度的矸石和断层引发的随机冲击不可预见，突然到达，且在单位时间内的到达次数少的概率大，到达次数多的概率小，而泊松过程可代表某段连续时间内事件发生的次数，故假设随机冲击以恒定的速率遵循齐次泊松过程到达。用()表示时刻之前冲击到达的次数，其概率密度函数为

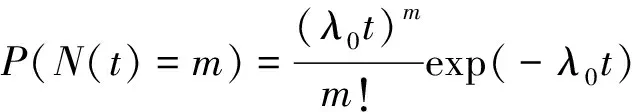
(4)

同一煤层中，煤岩硬度较为稳定，硬度很高或很低的概率都很小，由于正态分布的集中性、对称性和均匀变动性，故假设煤岩的硬度相互独立，且服从相同的正态分布。冲击的幅值代表夹杂在煤岩中的矸石和断层的硬度，因矸石和断层的硬度较高，故采用截断正态分布对其进行描述，即～(,)，其中，为均值，为标准差，其概率密度函数为

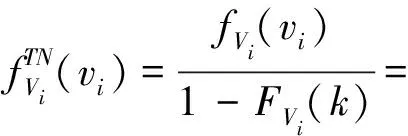
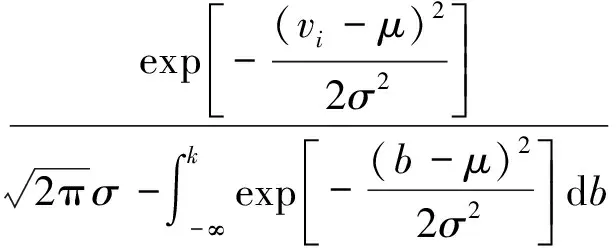
(5)

式中，为冲击幅值的最小值；()为冲击幅值对应的概率密度函数；()为冲击幅值对应的分布函数在冲击幅值为时的取值，即冲击幅值≤的概率；为积分计算中的中间变量。

高硬度的矸石和断层具有一定体积，将截割此类硬岩所需的时间定义为冲击持续时间s。考虑到冲击持续时间短的概率大，冲击持续时间长的概率小，且不同冲击的持续时间彼此无关，而指数分布可以用来表示独立随机事件发生的时间间隔，且具有无记忆性，故假设冲击的持续时间s服从参数为的指数分布，即s～()，其中，s≥0，为均值，其概率密度函数为

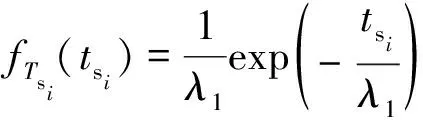
(6)

式中，s为随机变量s的取值。

1.3 随机载荷冲击下的退化建模

1.3.1 随机载荷冲击下的自然磨损退化()

截齿在截割煤岩的过程中，除去由高硬度的矸石和断层引起的冲击持续时间内的加速退化阶段外，截齿均处于煤岩引起的自然磨损退化阶段。若在时刻之前，截齿遭受了次冲击，则自然磨损退化量()为

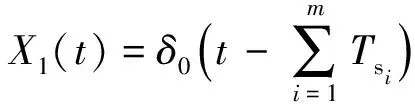
(7)

此外，如果在冲击持续时间s期间发生新的冲击，则当前的冲击过程将中止。

1.3.2 随机载荷冲击下的瞬时退化()

由于煤岩硬度突变，随机载荷冲击会在其到达的瞬间造成截齿的突然退化，从而引起退化量的突然增加。根据工程实践，矸石和断层的硬度越高，冲击幅值越大，造成的瞬时退化量也越大，即截齿的瞬时退化量和冲击幅值成正相关，故假设瞬时退化量与冲击幅值为线性关系，即=，其中，为线性关系常数。若在时刻之前，截齿遭受了次冲击，则瞬时退化量()为

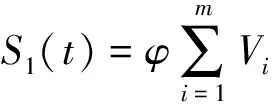
(8)

式中，为第次冲击的幅值。

1.3.3 随机载荷冲击下的加速退化()

由于矸石和断层具有一定的体积且硬度高于煤岩，故在其引起的冲击持续时间内，截齿发生加速退化。不同持续时间内的加速退化率为=，为退化率加速因子，其中>1。根据工程实践，矸石和断层的硬度越高，冲击的幅值越大，退化率加速因子也越大，即截齿在冲击持续时间内的退化率加速因子和冲击幅值成正相关。随着矸石和断层硬度的增加，截齿磨损的加速退化率呈指数式增长；同时，由于指数函数在自变量为正数时的函数值始终大于1，能够反映不同冲击幅值下退化率加速因子对截齿退化的加速影响，故假设退化率加速因子=exp()，其中，为指数关系常数。若在时刻前，截齿遭受了次冲击，则在冲击持续时间内的加速退化量()为

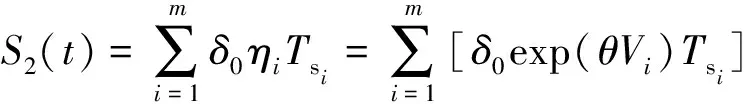
(9)

1.3.4 退化影响下的硬失效阈值()

在磨损的过程中，截齿抵御致命性冲击的能力逐渐减弱，如图3所示，随着总退化量连续增加，硬失效阈值逐渐减小，即截齿的硬失效阈值和总退化量成逆相关。假设硬失效阈值与总退化量为线性关系，则在时刻，截齿的硬失效阈值()为

()=h-()

(10)

式中，为线性关系常数。

1.4 概率密度模型

1.4.1 自然磨损退化量()的概率密度函数

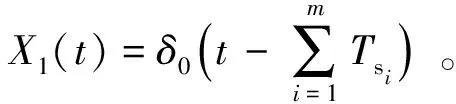
由于多个独立同分布的指数分布和的分布为Gamma分布，故其参数为冲击到达的次数和指数分布的参数，即～Gamma(,)，其概率密度函数(|()=)为

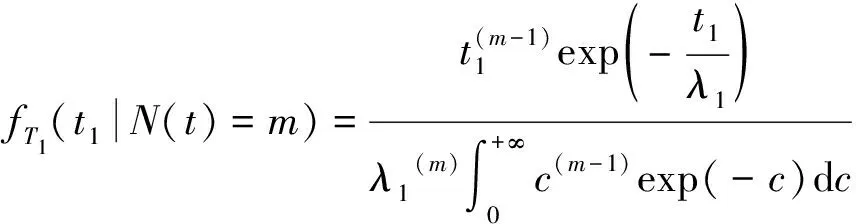
(11)

设随机载荷冲击下自然磨损退化时间为，则=-，其概率密度函数(|()=)推导可得

(|()=)=((-)|()=)=

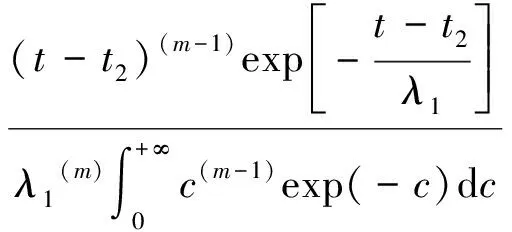
(12)

式中，为积分计算中的中间变量；为次冲击持续时间的和；为随机载荷冲击下自然磨损退化时间。

截齿的自然磨损退化量()=，其概率密度函数(|()=)推导可得

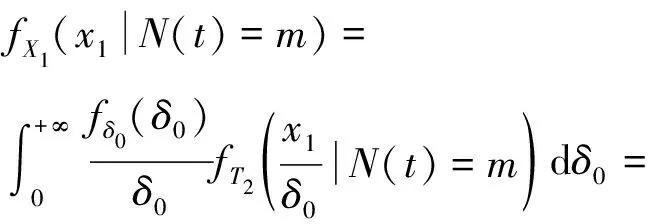
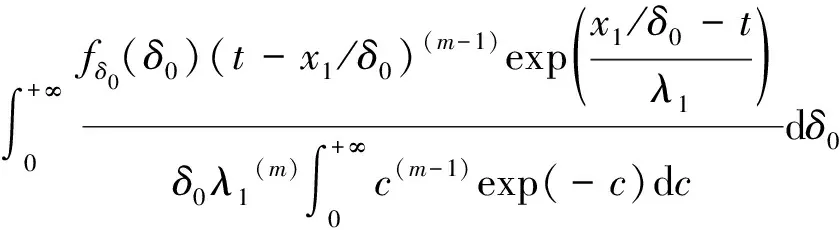
(13)

1.4.2 瞬时退化量()的概率密度函数

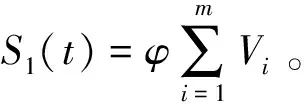
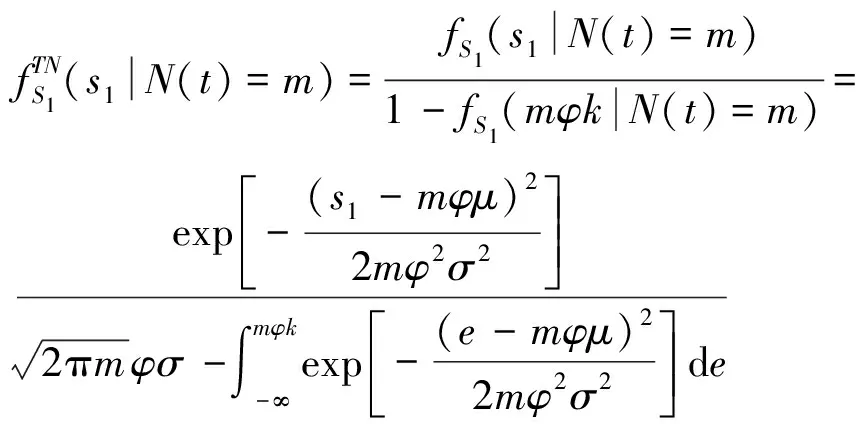
(14)

式中，为积分计算中的中间变量。

1.4.3 加速退化量()的概率密度函数

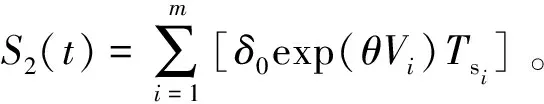
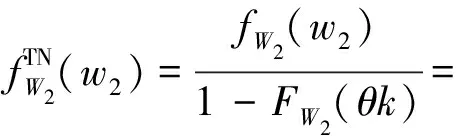
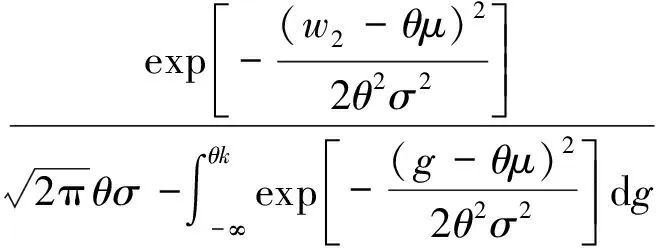
(15)

设退化率加速因子=exp()，其概率密度函数()推导可得

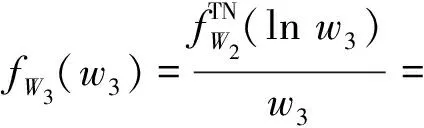
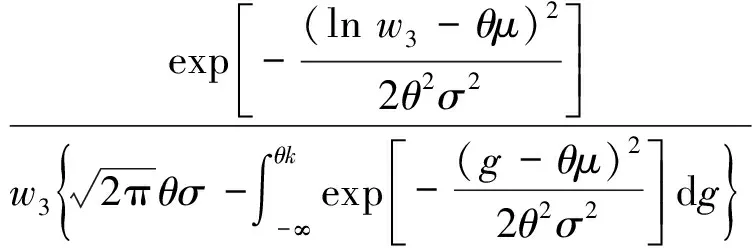
(16)

设加速退化率=，其概率密度函数()推导可得

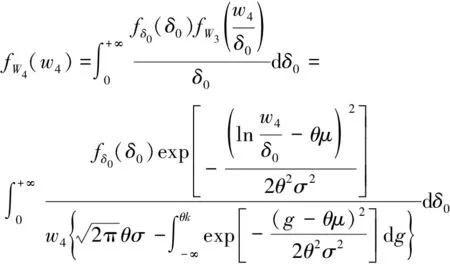
(17)

设单次冲击持续时间内的加速退化量=s，其概率密度函数()推导可得

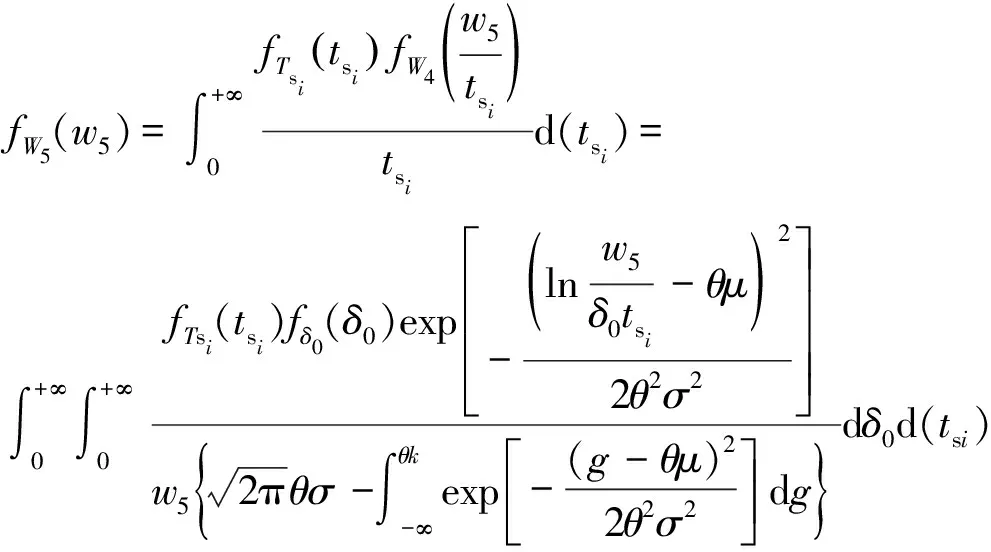
(18)

式中，，，，为随机变量，，，的取值。

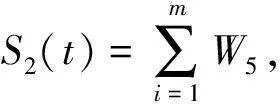
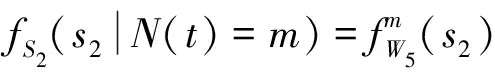
(19)

1.4.4 截齿总退化量()和截齿高度()的概率概率密度函数

由式(2)可知，截齿在竞争失效模式下的总退化量为()=()+()+()，若在时刻之前，截齿遭受了次冲击，则()的概率密度函数(|()=)推导可得

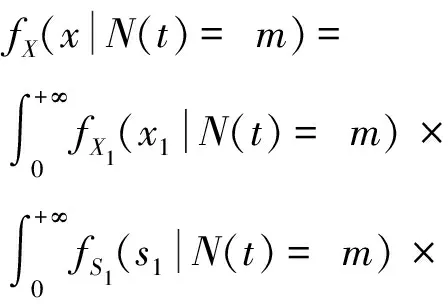
[(--)|()=]dd

(20)

由式(1)可知，截齿在竞争失效模式下的高度为()=(0)-()。若在时刻之前，截齿遭受了次冲击，则()的概率密度函数(|()=)推导可得

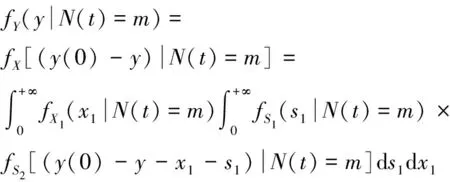
(21)

2 竞争失效下截齿磨损可靠性建模

截齿的失效是磨损退化导致的软失效和随机载荷冲击导致的硬失效相互竞争的结果，首先需要分别分析不同失效方式下截齿的可靠性，然后再进行竞争失效模式下的可靠性建模。

2.1 软失效下的截齿可靠性建模

当截齿的高度()低于软失效阈值时，截齿发生软失效。考虑到随机载荷冲击的影响，软失效和硬失效是相互依赖的，并且当不同数量的冲击到达时，磨损退化过程是不同的，因此针对以下两种情况，导出了在固定数量冲击到达的情况下，截齿从软失效中幸存的概率。

2.1.1 情况1：冲击次数为0

当时刻前没发生随机冲击，即()=0时，截齿的高度()只受长期连续自然退化影响。当仅考虑软失效时，截齿在时刻的可靠性函数为

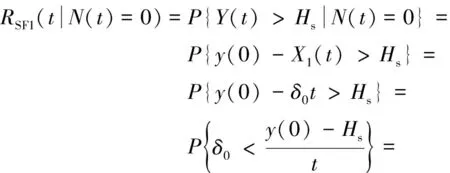
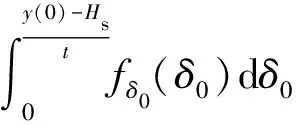
(22)

2.1.2 情况2：冲击次数不为0

当时刻之前冲击到达的次数()=>0,=1,2，……时，截齿的高度()同时受到长期连续自然退化、冲击引起的瞬时退化和不同冲击持续时间内变速率加速退化的影响。当仅考虑软失效时，截齿在时刻的可靠性函数为

(|()=)={()>|()=}=

1-{()<}=

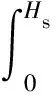
(23)

2.2 硬失效下的截齿可靠性建模

当截齿所受冲击的幅值高于截齿在时刻的硬失效阈值()，即-()>0时，截齿发生硬失效。由式(10)可知，截齿在竞争失效模式下硬失效阈值为()=h-()，设冲击幅值和硬失效阈值()的差值为()，其表达式为

()=-()=+()-h

(24)

设=()-h，若在时刻之前，截齿遭受了次冲击，其概率密度函数(|()=)推导可得

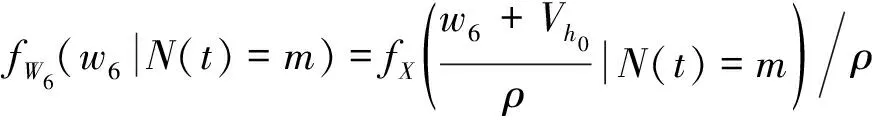
(25)

冲击幅值和硬失效阈值()的差值()=+，若在时刻之前，截齿遭受了次冲击，则()的概率密度函数(|()=)推导可得

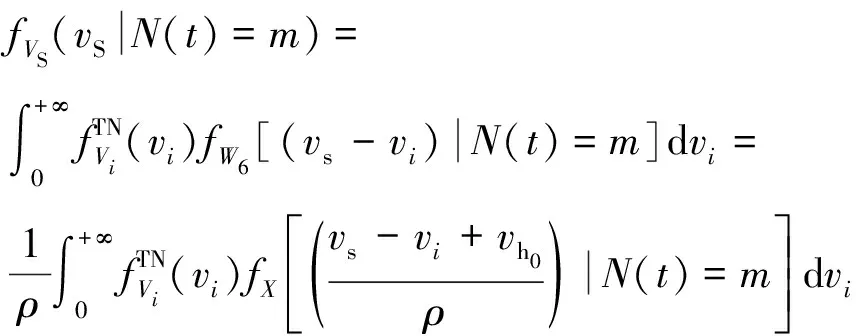
(26)

根据第1节的描述，截齿从随机冲击中幸存的概率为(0)。因此，当冲击到达的次数()=>0,=1,2，……时，仅考虑硬失效，截齿在时刻的可靠性函数为

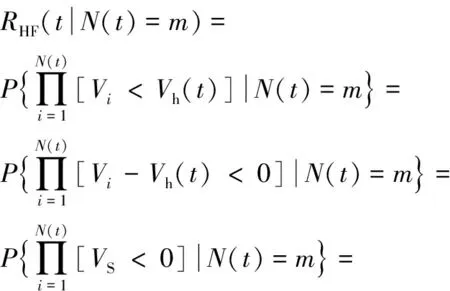
(27)

2.3 竞争失效下的截齿磨损可靠性建模

截齿失效是软失效和硬失效相互竞争的结果，在2.1节和2.2节中分别推导了它们在固定数量随机冲击下的可靠性函数。因此，截齿在时刻竞争失效的可靠性函数推导可得

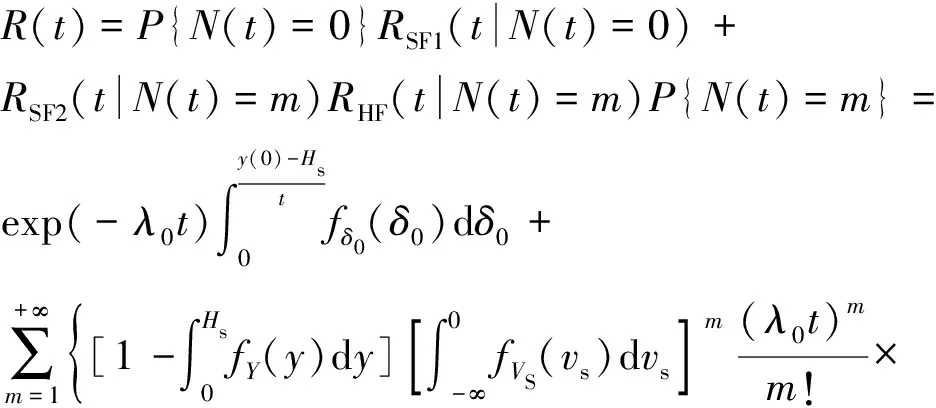
exp(-)}

(28)

3 数值算例

3.1 试验概述

相较于采煤机、连采机和掘锚机，掘进机长期处于高温、高压、强冲击、浓粉尘的恶劣工况，地质条件最为复杂，矸石和断层的分布最多，硬度最高，变化范围最大；同时掘进机的截割轨迹最为复杂，截齿磨损速度最快，消耗量最大，更能体现自然磨损退化和随机载荷冲击对截齿退化的综合影响，故笔者采用掘进机的工程数据对截齿的可靠性进行分析。

硬岩截割是悬臂式掘进机最重要的发展方向，全岩巷道、夹矸巷道等复杂坚硬巷道在我国掘进巷道中所占比例已达30%左右。受截齿材料、地质条件等因素的限制，目前悬臂式掘进机可经济截割的煤岩最大普氏硬度为10。随着所截割岩石硬度的逐渐增大，截齿的可靠性和消耗问题日益突出，因此，如何在兼具破岩能力的同时提高截齿的可靠性，是实现悬臂式掘进机经济运行的关键。

选取某煤机企业截割功率为260 kW的小断面岩巷掘进机进行截割试验。掘进机采用纵轴式截割头，试验期装配材料为35CrMnSi，42CrMo，40Cr，40Mn2B，35MnP等不同品质的截齿。不同材料的截齿耐磨性能不同，磨损退化率不同。掘进巷道断面为矩形，宽4.4 m，高2.9 m，断面面积为12.76 m；巷道岩性以灰白色中粒砂岩和灰黑色砂质泥岩为主，平均普氏硬度为6.8，其中伴有高硬度的矸石和断层。试验期的工况和截齿的失效状态分别如图4，5所示。

图4 掘进机截割试验

首先，在截割试验中，对矸石和断层引起的随机载荷冲击相关数据的获取，采用的是较为成熟的煤岩在线识别系统。该系统包含16路反映载荷变化的在线监测传感器，以及动态信号分析仪、工控机和显示器。通过采用多传感器特征信号样本对RBF神经网络进行学习和训练，完成动载荷的智能分析，从而实现对矸石和断层硬度、到达次数以及持续时间的在线监测与精确识别。对截齿磨损相关数据的获取，结合煤岩识别系统的测量结果，采用的方法为非周期离线检测。其次，利用大量的试验数据及专家经验，针对各个随机变量，采用数据拟合软件进行了多种分布的极大似然估计，同时通过拟合优度检验并选择了最佳分布，从而将最佳分布作为本文所假设的分布。对于关系模型中的参数，则采用线性和非线性回归得到。试验中测量的数据包括截齿的自然退化量、瞬时退化量、加速退化量、总退化量、矸石和断层的硬度、到达次数和持续时间等，各种数据的测量设备、测量方式和所拟合的参数见表1。

图5 截齿失效情况

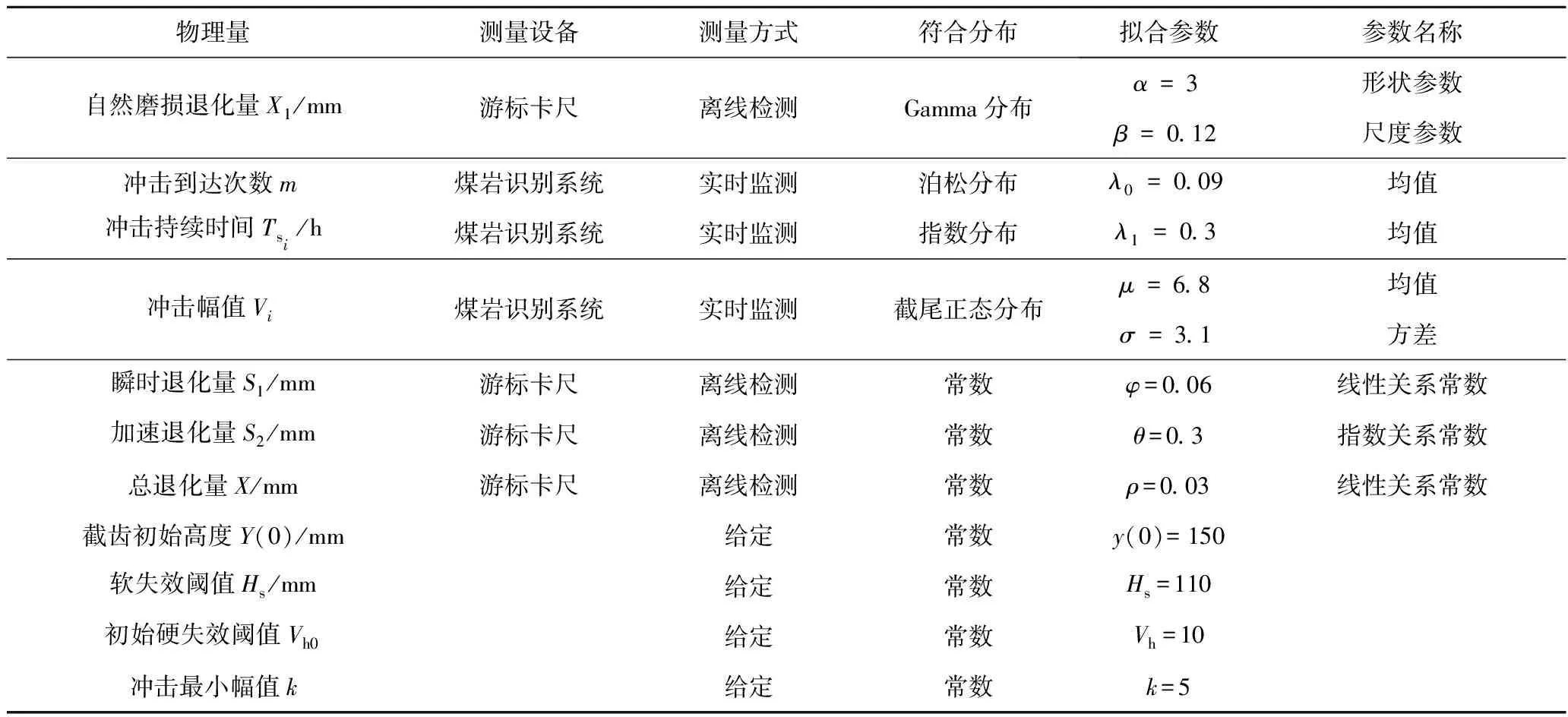
表1 参数

值得一提的是，现阶段关于采掘机械截齿磨损状态的在线监测系统已经得到了初步的研究和应用，该系统包含3路反映截齿磨损状态的在线监测传感器，以及动态信号分析仪、工控机和显示器。通过采用自适应神经-模糊推理系统多维模糊神经网络方法实现多传感特征信息的决策融合，实现截齿磨损程度在线监测与精确识别。若能通过截齿磨损在线监测系统获取截齿磨损的实时数据，就可对相关参数进行更为精确的估计，从而借助本文提出的模型，对截齿的可靠性进行实时的动态评估。

3.2 模型对比

为了考虑影响截齿失效过程的不同因素，并验证模型的通用性，通过设置不同的参数，将建立的可靠性模型转化为了考虑不同因素的可靠性模型。表2中比较了这些模型所考虑的主要因素。

为了说明瞬时冲击、冲击持续时间和不同冲击持续时间内变速率退化以及硬失效阈值变化对截齿可靠性的影响，根据表1给出的参数，将表2中列出的5种模型的可靠性曲线绘制在图6中，由此可以得出：

表2 影响截齿失效过程的主要因素比较

(1)瞬时冲击对截齿失效过程的影响可以通过比较模型1和模型2的可靠性曲线得出。由图6可知，只考虑自然退化的截齿具有7 d的高稳定可靠性阶段，即截齿在7 d内不会发生失效，这和截齿的应用实际存在巨大差异。而考虑自然退化和瞬时冲击竞争失效的截齿直接进入快速退化阶段，不具有高稳定可靠性阶段，截齿在7 d时的可靠性只有0.44，即截齿在7 d内不发生失效的概率只有44%，这符合截齿的实际退化趋势。这是因为随机冲击会在其到来的瞬间使截齿突然退化，加速了截齿的退化过程，且考虑软失效和硬失效的竞争失效模式时，任何一种失效的发生都会导致截齿失效，故考虑自然退化和瞬时冲击竞争失效的模型比只考虑自然退化失效的模型具有更低的可靠性水平。

(2)冲击持续时间对截齿失效过程的影响可以通过比较模型2和模型3的可靠性曲线得到。由图6可知，不考虑冲击持续时间的截齿可靠性在10 d时为0.34，考虑冲击持续时间的截齿可靠性在10 d时为0.19，截齿失效的概率增加了15%。这是因为如果不考虑冲击持续时间，冲击只会在其到来的瞬间使截齿突然退化。然而，当考虑冲击持续时间时，截齿会在不同的冲击持续时间内加速退化，同时相应的缩短了自然退化时间。当冲击持续时间存在时，忽视其对截齿失效过程的影响，会高估截齿的可靠性，故考虑冲击持续时间的模型总是比不考虑冲击持续时间的模型具有更低的可靠性水平。

(3)不同冲击持续时间内变速率退化对截齿失效过程的影响可以通过比较模型3和模型4的可靠性曲线得到。由图6可知，不考虑变速率的截齿可靠性在10 d时为0.19，考虑变速率的截齿可靠性在10 d时为0.16，截齿失效的概率增加了3%。这是因为假设不同冲击持续时间内截齿的退化率不变，实际上是对冲击持续时间内退化过程的简化，在实际中，冲击持续时间内截齿磨损的退化率与冲击的幅值相关，忽视变速率退化过程，会导致截齿可靠性计算不准确，故不同冲击持续时间内，考虑变速率退化的模型总是比不考虑变速率退化的模型具有更准确的可靠性水平。

(4)硬失效阈值变化对截齿失效过程的影响可以通过比较模型4和模型5的可靠性曲线得出。由图6可知，不考虑硬失效阈值变化的截齿可靠性在10 d时为0.16，考虑硬失效阈值变化的截齿可靠性在10 d时为0.13，截齿失效的概率增加了3%。这是因为随着磨损程度的增加，截齿的硬失效阈值会随着总退化量的增加而减小，截齿抵御致命性冲击的能力降低，对硬失效更加敏感，发生硬失效的概率增大，忽视硬失效阈值变化对截齿失效过程的影响，会高估截齿的可靠性，故考虑硬失效阈值变化的模型总是比不考虑硬失效阈值变化的模型具有更低的可靠性水平。

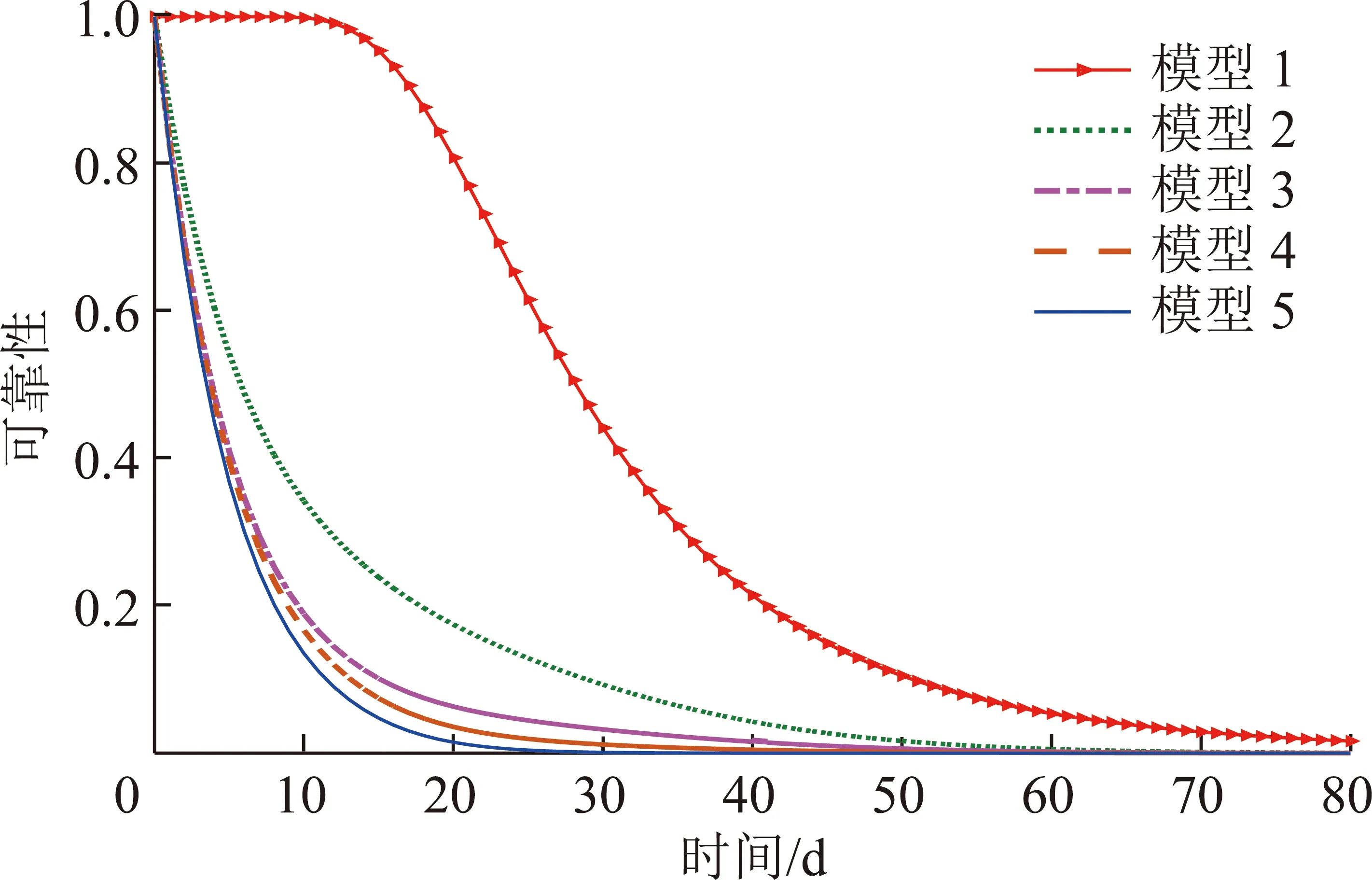
图6 截齿可靠性曲线

自然磨损退化和随机载荷冲击共同作用下截齿竞争失效的可靠性曲线，如图6中模型5所示。由图6可知，截齿在整个生命周期中不存在高稳定可靠性阶段，从开始截割煤岩起，就进入了竞争失效模式下的快速退化阶段，可靠性曲线呈现急剧下降。由图6可见，截齿能使用5 d的可靠性仅为0.5，这正是截齿作为高消耗配件，更换频繁的重要原因。因此，当截齿可靠性超出可接受的范围时，需要进行必要的更换。

3.3 灵敏度分析

为了改进截齿可靠性以指导截齿进行最优更换储备和优化设计，有必要分析模型参数的灵敏度，从而探讨其对可靠性的影响。从第2节的模型描述来看，所提出的截齿退化模型具有创新性，并符合采掘机械的工程实际，其中参数，，，，，和为反映截齿自然磨损退化和随机载荷冲击的关键参数，因此，分析了以上参数的灵敏度，具体的参数设定见表3，详细结果如图7～13所示。

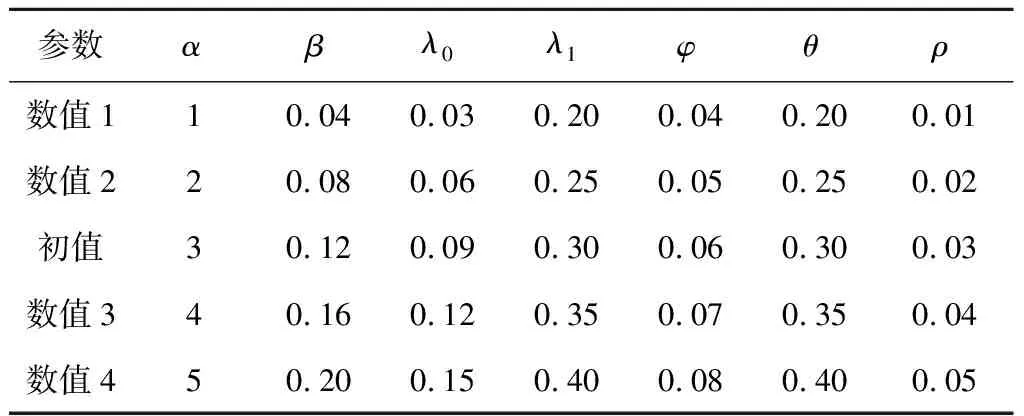
表3 参数灵敏度设定值

对自然退化率的形状参数和尺度参数的灵敏度分析如图7，8所示。当从5减小到1时，截齿在5 d时的可靠性提高了0.117 7；当从0.20减小到0.04时，截齿在10 d时的可靠性提高了0.148 5。故降低或，截齿的可靠性均有所提高，且随着截齿工作时间的增加，影响愈加明显，这说明软失效对截齿失效的贡献呈逐步增大的趋势。实际中，代表影响截齿磨损的客观属性，即截齿的材料成分、外形结构、加工工艺和安装角度，故可以通过加强截齿材料强度、优化截齿结构设计、改良截齿热处理工艺、调整截齿的安装角度以及利用表面强化技术等方式，使截齿具有更好的耐磨性，降低截齿的自然退化率，从而减小截齿的自然磨损和加速磨损退化量，降低软失效的可能性，提高截齿的可靠性。

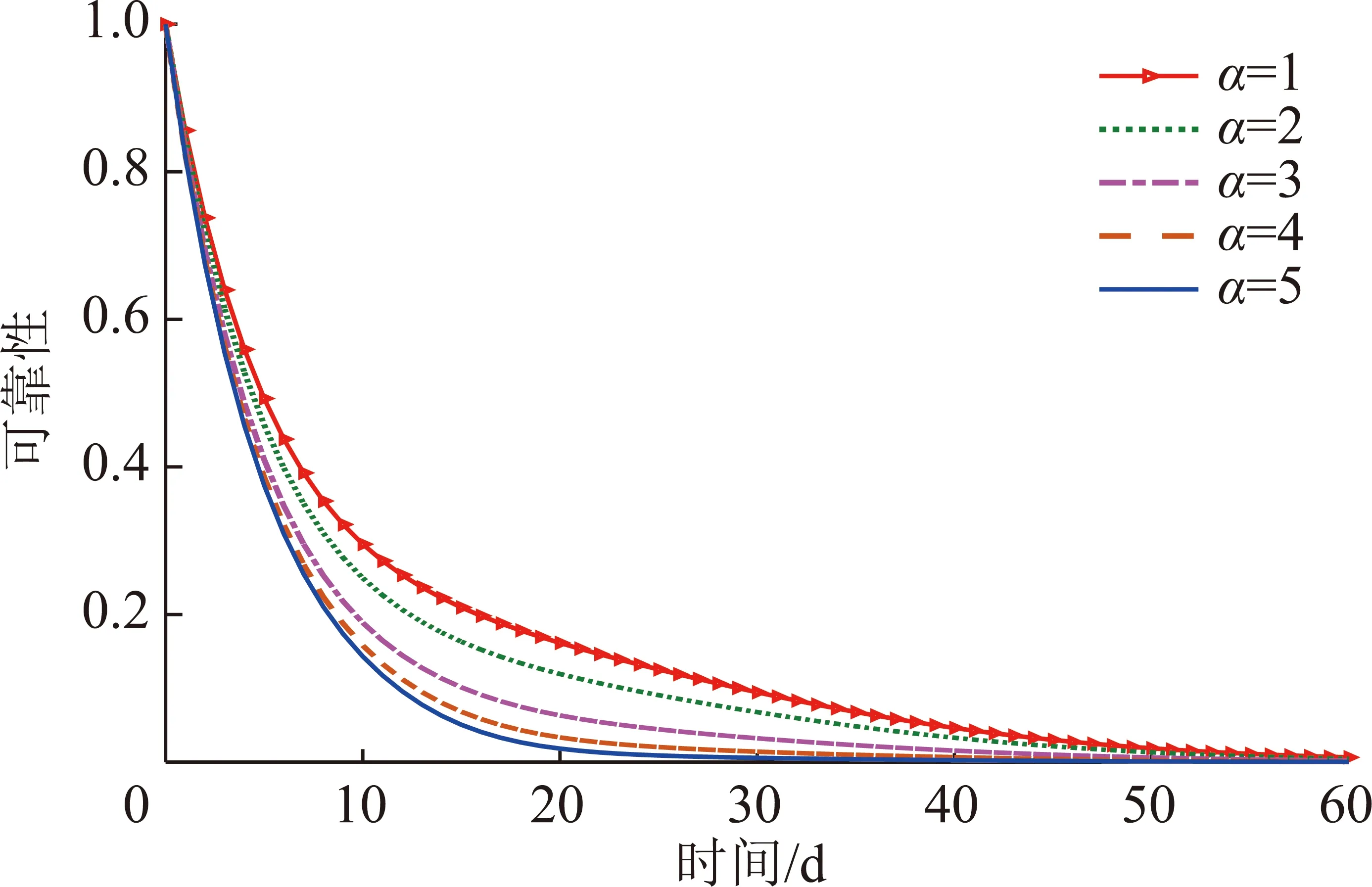
图7 不同α下截齿可靠性的灵敏度分析

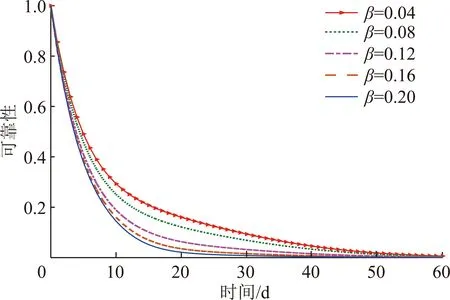
图8 不同β下截齿可靠性的灵敏度分析

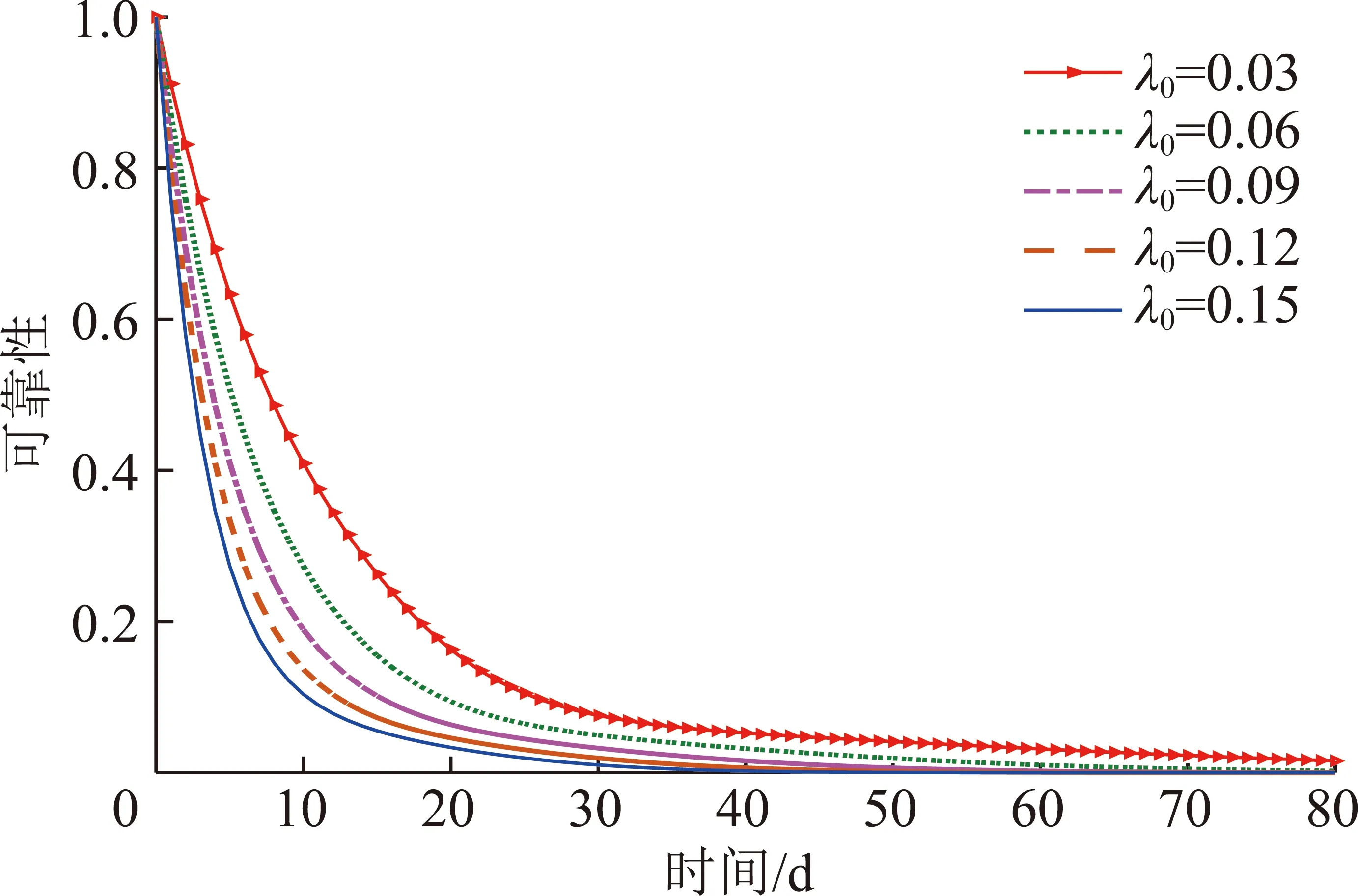
图9 不同λ0下截齿可靠性的灵敏度分析

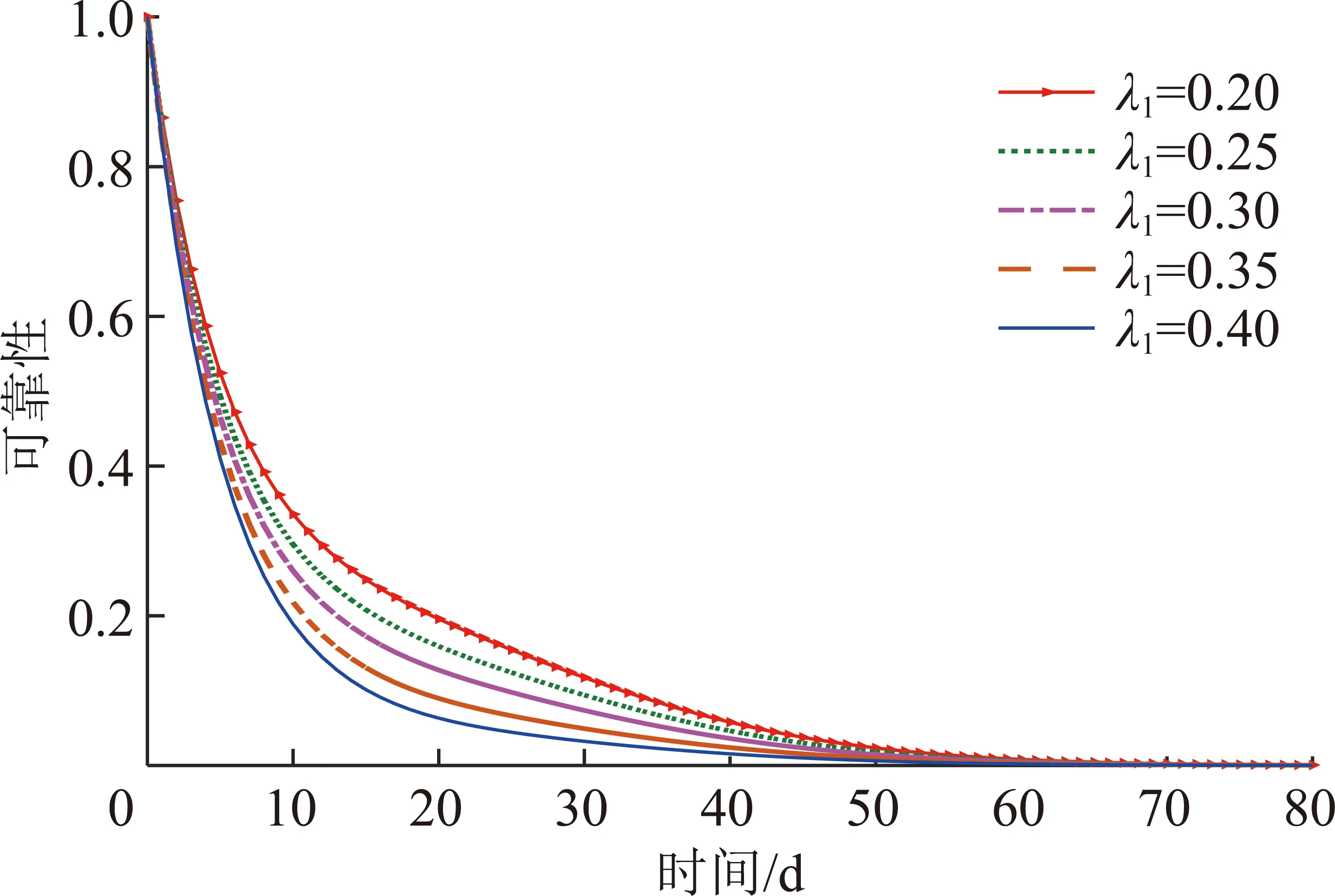
图10 不同λ1下截齿可靠性的灵敏度分析

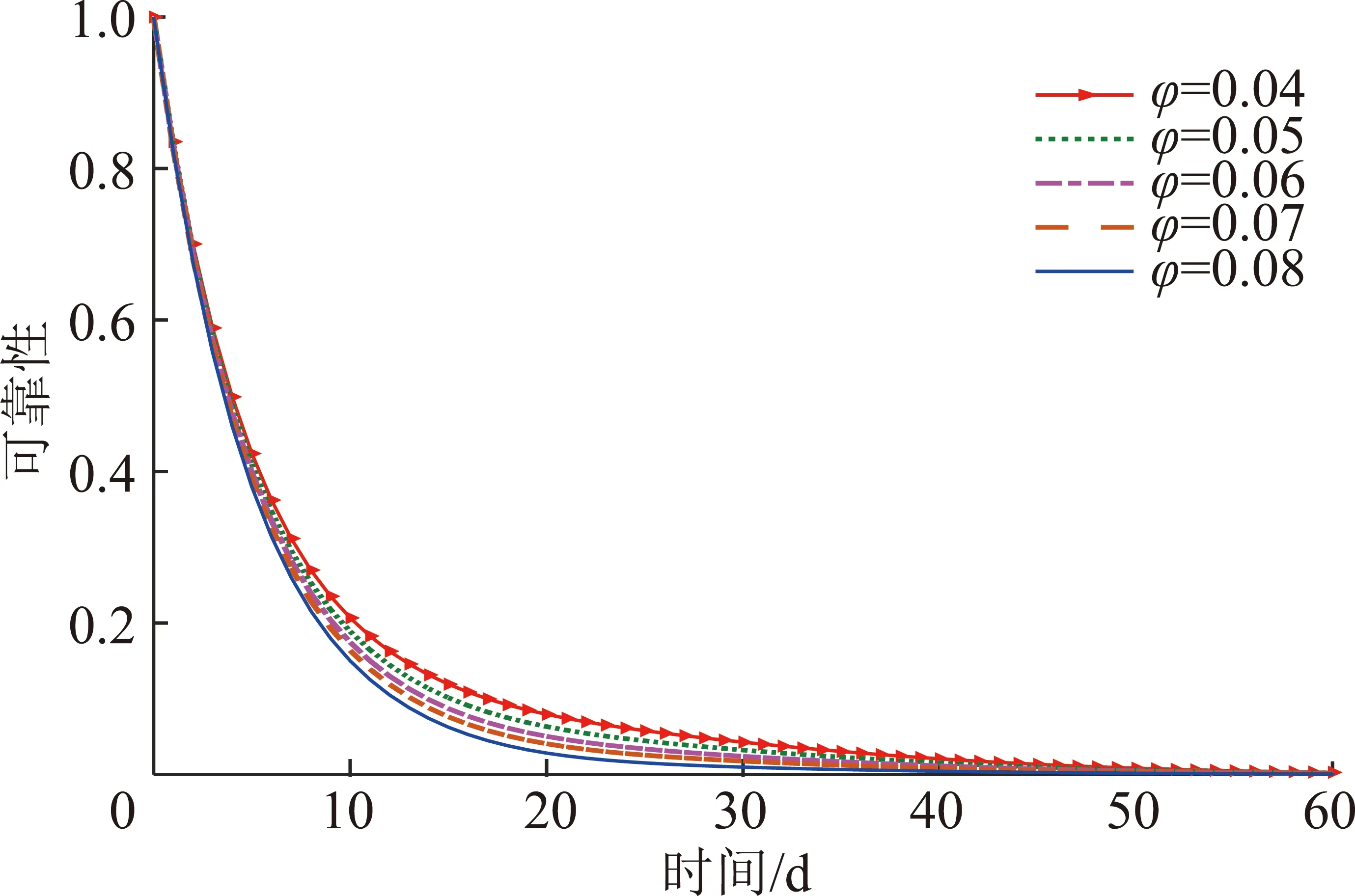
图11 不同φ下截齿可靠性的灵敏度分析

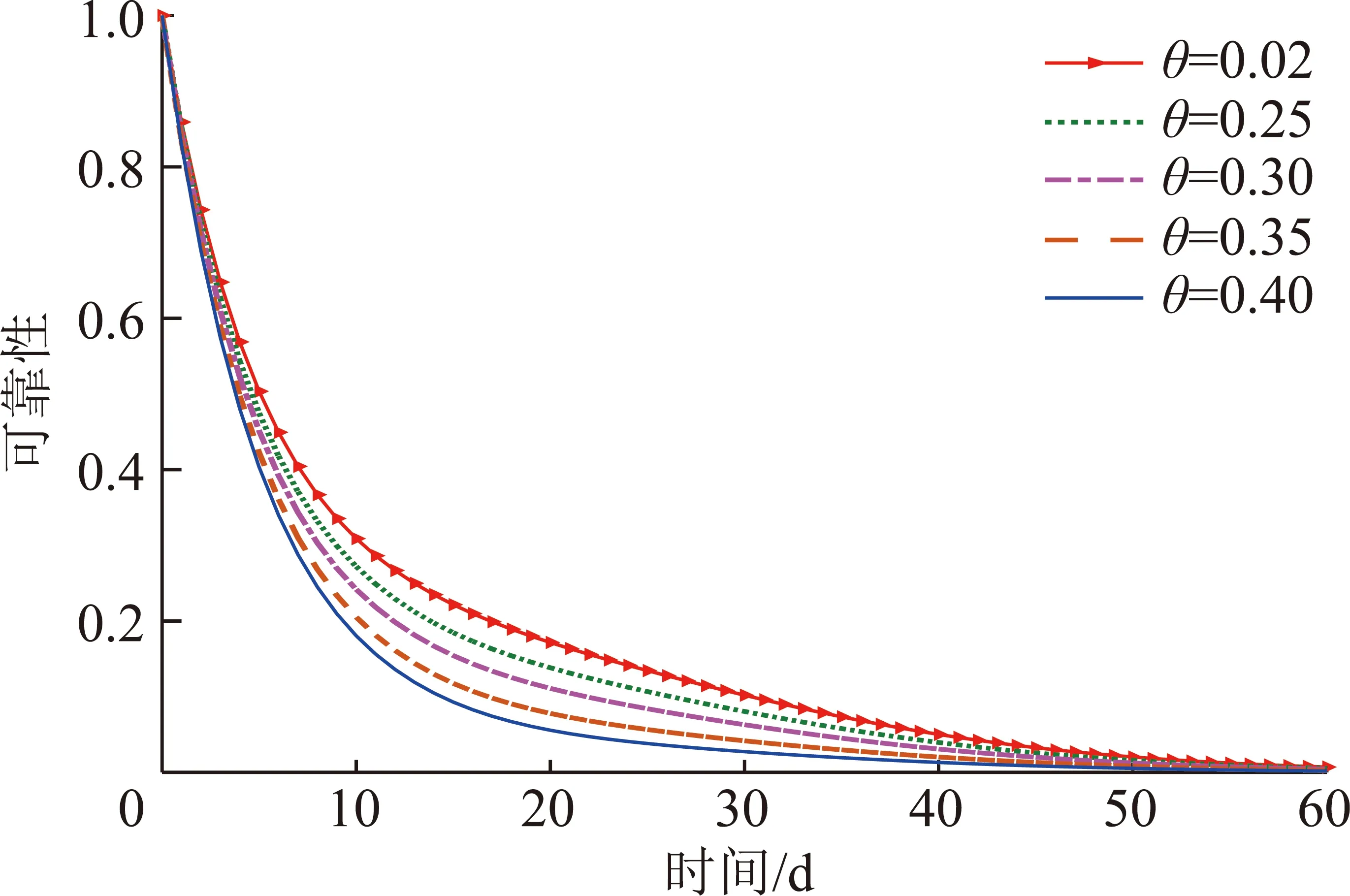
图12 不同θ下截齿可靠性的灵敏度分析

对冲击到达次数的分布参数和冲击持续时间的分布参数的灵敏度分析如图9，10所示。当从0.15减小到0.03时，截齿在10 d时的可靠性提高了0.305 7；当从0.4减小到0.2时，截齿在10 d时的可靠性提高了0.146 8。故降低或，截齿的可靠性均有所提高。在截齿工作的初始阶段就对其可靠性有明显影响，且影响较大；在截齿工作的初始阶段对其可靠性影响较小，在初始阶段后，影响才逐步显现。这说明冲击到达的频率比冲击持续时间对截齿可靠性的影响更大。实际中代表矸石和断层在煤层中的位置分布，故应在实际生产前对煤层进行详细的地质探测，了解矸石和断层在煤岩中的布局，同时在生产过程中应用煤岩实时识别技术，在线监测煤岩的属性和变化，动态调整采掘机械的施工层位，规划采掘机械的截割轨迹，使截齿尽可能避免在过短的时间内频繁的遇到高硬度的矸石和断层，从而减小随机载荷冲击引起的瞬时退化量和加速退化量；代表矸石和断层的体积，故应在设计中提高采掘机械的截割能力或改变破岩方式，研发适用于硬岩截割的采掘机械，以用更短的时间截割相同体积的矸石和断层，减少冲击持续时间，从而减小冲击持续时间内的加速退化量，提高截齿的可靠性。

对瞬时退化量和冲击幅值的线性关系常数、冲击持续时间内退化率加速因子和冲击幅值的指数关系常数的灵敏度分析如图11，12所示。当从0.08减小到0.04时，截齿在10 d时的可靠性提高了0.056 7；当从0.4减小到0.2时，截齿在10 d时的可靠性提高了0.128 5。故降低或，截齿的可靠性均有所提高。和在截齿工作的初始阶段对其可靠性影响较小，在初始阶段后，影响逐步显现，且的影响更为明显。这说明在截齿退化过程中，变速率加速退化比瞬时退化对截齿可靠性的影响更大。实际中，代表截齿与矸石和断层的相互关系，故可对截齿与矸石和断层的接触角度、接触面积、接触载荷特性以及相对运动特性进行优化，以减少矸石和断层对截齿退化的影响，从而减小随机载荷冲击引起的瞬时退化量和加速退化量，提高截齿的可靠性。

对截齿硬失效阈值和总退化量的线性关系常数的灵敏度分析如图13所示。当从0.05减小到0.01 时，截齿在10 d时的可靠性提高了0.031 5，故降低，截齿的可靠性有所提高。在截齿工作的初始阶段对其可靠性的影响可以忽略不计，在初始阶段之后对其可靠性的影响逐步增加。越大，截齿的硬失效阈值下降越快，截齿发生硬失效的可能性越大。这说明在截齿工作的初始阶段硬失效不是其主要的失效模式，在初始工作阶段后，硬失效对截齿失效的贡献开始逐渐增大。实际中代表截齿抵御致命性冲击能力下降的速率，故可在保证冲击韧性的基础上，对截齿不同高度下材料的硬度进行均匀化处理，以减少磨损对截齿硬失效阈值的影响，从而减小截齿发生硬失效的可能性，提高截齿的可靠性。

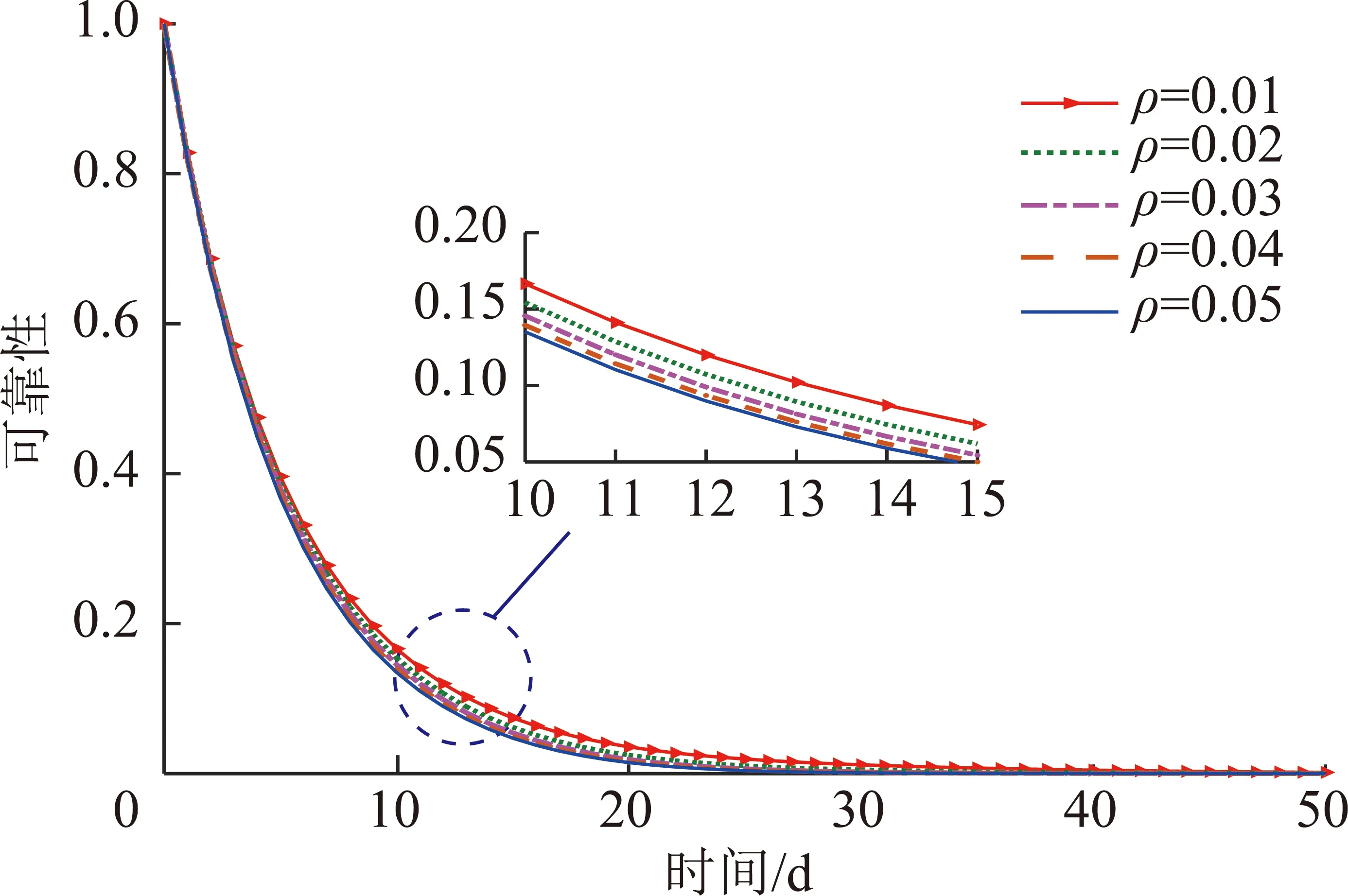
图13 不同ρ下截齿可靠性的灵敏度分析

灵敏度分析表明，考虑随机冲击影响下的竞争失效过程对截齿的可靠性评估有显著影响。利用本文提出的模型，截齿的设计者、制造商和维护者将更好地了解截齿的竞争失效过程，并获得更准确的可靠性评估结果。此外，还可以进行以提高可靠性为目标并考虑成本约束的优化设计，帮助现场从业人员选择合适的模型参数，有效提高截齿的可靠性。

4 结 论

(1)为了更好地反映截齿磨损退化和随机载荷冲击的相互影响，构建了同时考虑自然磨损退化、瞬时冲击退化以及冲击持续时间内变速率加速退化过程的冲击退化模型。

(2)结合磨损退化和随机载荷冲击的竞争失效机制，构建了截齿的可靠性模型，更好的反映了磨损退化和随机载荷冲击对截齿退化过程的综合影响。

(3)基于工程数据对截齿的可靠性模型进行了数值实验，并验证了该模型的有效性。从灵敏度分析可以看出，考虑持续冲击、变速率加速退化和硬失效阈值变化的截齿竞争失效可靠性模型更符合实际，并可为截齿的设计优化和可靠性改进提供了有效指导。

在工程实践中，由于在采掘机械截割滚筒中所处的位置和角度不同，不同截齿受力不同，磨损规律不同。因此，有必要进一步对采掘机械集成有多个截齿的截割系统进行多部件系统的可靠性研究，从而在此基础上，进行截齿维修决策和备件储备问题的研究。