基于WSR和组合赋权的装配式建筑技术应用成熟度评价研究
高 洁,周 伟
(1.长江工程职业技术学院, 武汉 430212;2.武汉城建集团2049集团, 武汉 430010)
1 引 言
随着我国工业化、城市化的快速发展,传统建筑业在带动经济高速增长的同时,环境压力也日趋严峻,实现绿色可持续发展,是建筑行业的时代要求。发展装配式建筑产业,是传统高排放建筑业实现碳达峰和碳中和战略目标的需要。截至2020年底,全国新开工装配式建筑共计6.3亿m2,较2019年增长50%,占新建建筑面积的比例约20.5%,超额完成了《“十三五”装配式建筑行动方案》确定的工作目标[1]。然而,在当前装配式建筑产业发展和技术应用的过程中,仍存在政策缺失、配套短缺、成本较高、接受程度较低等问题,导致了各地区产业发展和技术应用不均衡的现状。如何因地制宜的提升装配式建筑发展和技术应用水平,成为各地推广装配式建筑的研究重点。
2 基于WSR的装配式建筑技术应用成熟度评价指标体系构建
装配式建筑技术应用成熟度是指在装配式建筑技术在建设项目中的应用情况由从无到有、由低到高、由简单到复杂的进阶过程。合理制定和量化技术应用能力成熟度等级可以为其在项目的应用情况及其提升重点提供参照依据。
2.1 构建原则
装配式建筑技术应用成熟度评价是多层次、多维度的复杂系统,因此科学、全面的成熟度评价指标体系是成熟度模型的必要组成部分,是对装配式建筑技术应用水平进行科学评估的必要条件,可以帮助相关主体单位识别技术在项目应用中存在的不足和缺陷,为逐步提升装配式建筑技术应用水平提供参考,所以在评价指标选择时必须遵循全面性原则、科学性原则、通用性原则、真实性原则[2]。
2.2 能力成熟度等级的划分
成熟度等级的划分应涵盖装配式建筑技术应用的各阶段。装配式建筑技术应用水平是一个逐步提升的过程,充分考虑其技术应用发展特点,借鉴CMM[3]的思想和标准,将成熟度等级划分:初始级、起步级、发展级、成熟级、提升级。各等级评分范围划分及等级特征详见表1。

表1 成熟度评价等级划分
2.3 评价指标体系的构建
“物理(Wuli)-事理(Shili)-人理(Renli)”方法论简称WSR,是由顾基发教授与朱志昌博士提出来的一种方法理论,也是一种分析、解决复杂系统问题的工具[4]。本文搜集汇总了装配式建筑相关文献中对装配式建筑技术发展具有一定影响的相关指标,并基于物理、事理、人理3个维度对相关指标进行分类。为使指标体系更加科学、合理,通过专家调查问卷的方法对相关指标进行打分筛选,选取与评价模型关键要素关联度高的指标,最终确定3个维度共19项评价指标,如图1。
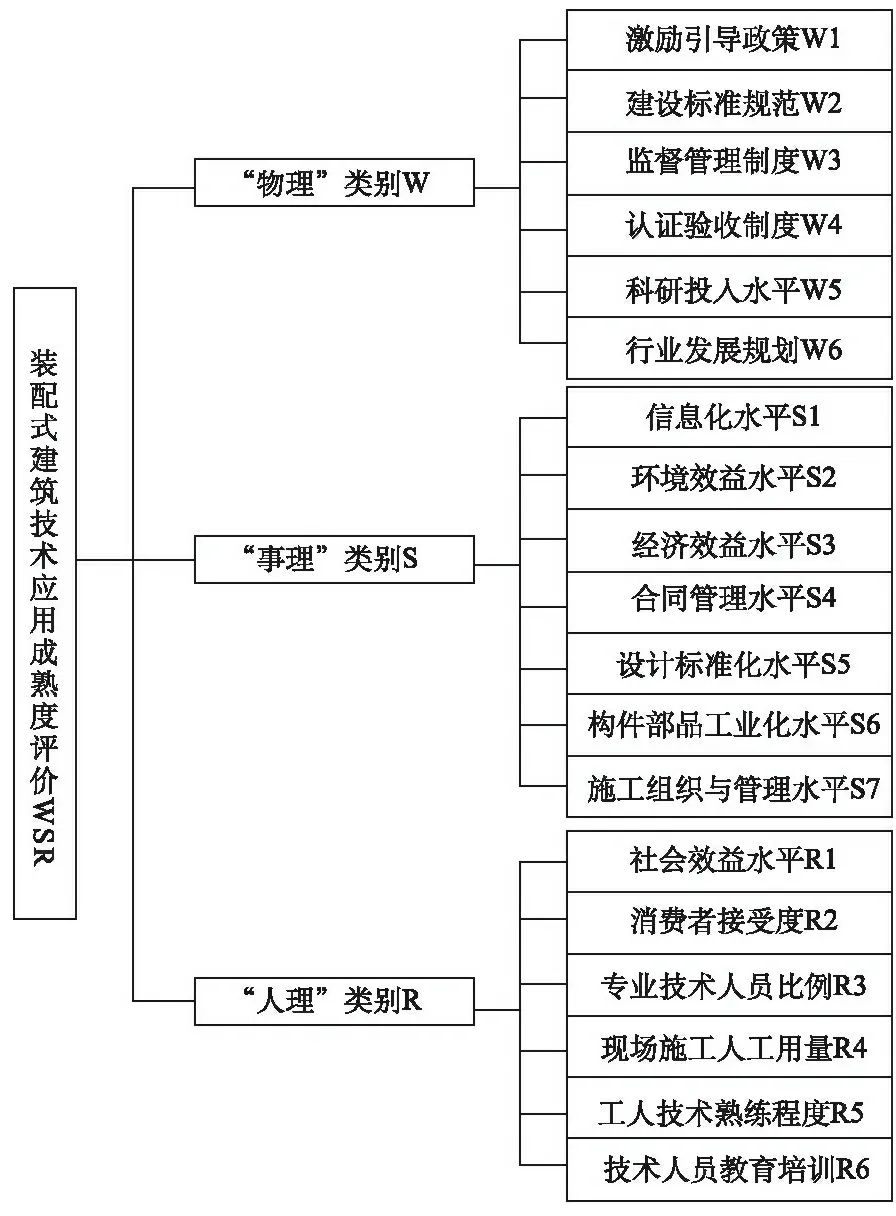
图1 装配式建筑技术应用成熟度评价指标体系
3 基于组合赋权的指标权重确定
由于装配式建筑技术应用成熟度评价指标的相关数据来自于专家个人判断,不可避免地带有个人主观色彩。为了使权重信息既体现专家经验判断力的权威性,又尽可能增强决策问题的客观真实性,避免与事实相悖,在确定指标权重时采用乘法合成的方式组合赋权,通过层次分析法确定主观权重,通过熵值法确定客观权重,以此在一定程度上确保指标重要程度的差异性[5]。
3.1 AHP确定主观权重
层次分析法(AHP)通过两两比较确定层次中各因素相对重要程度,并通过定量计算,确定各指标权重。在确定各层次各因素之间的权重时,通过引入“1~9标度法”对各层级因素进行两两重要性比较,即aij为要素i与要素j重要性比较结果。
为在重要性比较中避免出现逻辑性错误,通过专家打分的方式对各指标进行打分,通过各指标分数F的比值Fi/Fj来确定aij,即aij=Fi/Fj。各指标两两比较结果aij构成的矩阵称作判断矩阵A,判断矩阵A具有如下性质:aij=1/aji。对应于判断矩阵A最大特征根λmax的特征向量,经归一化后记为w。后利用式(1)求解判断矩阵A的最大特征根λmax,其对应的特征向量即为因素的权重值。
Aw=λw
(1)
一致性指标用CI计算,CI越小,一致性越大,引起的判断误差越小。因而可以用λ-n数值的大小来衡量A的不一致程度。通过式(2)计算,CI=0时,有完全的一致性;CI接近于0,有满意的一致性;CI越大,不一致越严重。
(2)
与此同时,为衡量CI大小,引入随机一致性指标RI,考虑到一致性的偏离可能是由于随机原因造成的,因此在检验判断矩阵是否具有满意的一致性时,还需将CI和随机一致性指标RI进行比较,得出检验系数CR,通过式(3)求解,如果CR<0.1,则认为该判断矩阵通过一致性检验,数据合理可用,否则就不具有满意一致性,数据不可用。其中RI可以直接根据表2取值。

表2 平均随机一致性指标RI标准值
(3)
3.2 熵权法确定客观权重
对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大,该指标对综合评价的影响(即权重)就越大。在熵值赋权法中,先将数据进行归一化处理,由于本文设计问卷得分计量单位一致,因此无需考虑指标正负,统一按式(4)进行归一化计算得到矩阵X。然后通过式(5)计算第j项指标在第i个类别中的占比pij,最后再通过式(6)和式(7)计算出各指标项熵值Ej和权值vj。
(4)
(5)
(6)
(7)
式中xij——第i个类别第j个指标分值(i=1,2,…,n;j=1,2,…,m)。
3.3 组合权重的计算
AHP-熵值法是主客观综合赋权的方法:通过层次分析法和熵值法对专家打分进行权重计算,分别求出主管权重向量和客观权重向量,然后将两者相乘,得到组合权重。设Wi=(w1,w2,…,wn)为AHP法所求权重值,Vi=(v1,v2,…,vn)为熵权法所求权重值,则组合权重值θj可通过式(8)进行计算。
(8)
4 基于未确知测度函数的综合评价模型
王光远在1990年提出未确知信息及其数学处理理论[6],用于处理多因素的不确定信息,并广泛应用于多个领域[7]。对于装配式建筑技术应用成熟度而言,其本身就是一个不确定性的问题,无法严格区分成熟与不成熟的界限。因此,引入未确知测度理论能够具体衡量装配式建筑技术应用成熟度情况,并将测度结果定量化描述。
4.1 确定评价空间的有序分割类
在装配式建筑技术应用成熟度问题中,根据物理、事理、人理将评价指标进行3个维度的划分,每个维度都是一个相对独立的整体,因此每个维度都可以作为一个对象进行研究,3个评价维度构成维度空间X=(X1,X2,X3),其中X1,X2,X3分别表示物理类别、事理类别和人理类别。5个评价等级组成评级空间U=(U1,U2,U3,U4,U5),其中U1,U2,U3,U4,U5分别表示初始级、起步级、发展级、成熟级、提升级,因此等级设定k+1级比k级高,即U1 若Cijk=C(xij∈Ck)表示第i个维度下的第j个指标因素的实测值xij属于第k个等级的程度,同时符合数学理论中的“非负有界性”、“归一性”和“可加性”条件,则称Cijk为未确知测度。对于未确知测度值Cijk,通常采用构造未确知测度方程的形式的计算。常用的构造方法有直线型、抛物线型和指数型等,本文综合考虑选取的指标特性和实际应用的难易程度,决定采用计算相对容易、应用广泛的直线型方法构造未确知测度方程,详见表3。将各成熟度指标数据xij代入即可得到单指标未确知测度矩阵(Cijk)m×p,其中m为评价指标维数,p为评价等级个数。 表3 未确知测度方程 (9) 装配式建筑技术应用成熟度等级空间U为有序分割类,在未确知测度理论中采用置信度识别准则来判断等级结果。设置信度λ>0.5(λ通常取0.6或0.7),若满足式(10),则认为被评价的装配式建筑技术应用成熟度位于第p0级,即评价等级为Up0。 (10) 为了进一步验证以上装配式建筑技术应用成熟度评价方法的可靠性与实用性,以装配式建筑项目案进行计算和分析。 该项目位于武汉市新洲区,占地面积16 660.57m2,建筑面积约4 651m2,容积率2.5,绿化率32.30%,规划户数364户,由3栋住宅(24F+32F+32F)组成,其中2#楼共32层,2-28层采用装配式建筑施工。该项目2#楼装配式住宅主要采用预制叠合楼板、预制叠合阳台板、ALC内隔墙等预制构件,根据设计要求进行现场吊装施工。 数据由该项目高层管理者、技术人员和参与走访的高校装配式建筑研究人员共计10人组成专家组,通过填写问卷的形式获得。其中层次分析法数据通过专家对各指标相对于该项目的重要程度采用10分制进行打分,然后对各专家打分进行均值计算,通过两两分值的比值作为判断矩阵数据。熵权法数据以及未确知指标矩阵数据同样采用10分制分别对各指标在该项目应用情况进行打分,然后进行均值计算。此处仅以“物理”维度为例进行计算演示。 5.1.1 组合权重计算 物理维度层次分析法判断矩阵如表4,由于本次AHP打分采用10分制对各指标重要程度进行单独打分,然后根据各指标分值两两相除得到相对分值,采用该打分机制,可以有效避免评分过程中出现A>B,B>C,C>A这样逻辑性错误,因此在求最大特征根时,最大特征根与矩阵阶数相等,CI=CR=0,判断矩阵均具有完全一致性。 表4 物理维度各指标判断矩阵 将物理维度熵权法打分数据代入式(4)-(8)计算,最终分别求出物理维度下主观权重wj、信息熵Ej、熵权值vj和组合权重θj,详见表5。 表5 物理维度各指标权重 5.1.2 未确知测度评价计算 (1)单指标未确知测度矩阵 根据表3确定的各等级未确知测度函数,将专家对于物理维度各指标评分均值数据代入,得到各维度单指标未确知测度矩阵分别如下: 通过式(4)-(9),将表5中计算出的各指标组合权重值θj与对应的单指标未确知测度矩阵(CWjk)6×5逐层级相乘,最终可得到多指标综合测度矩阵: (CWk)=(0 , 0.264 8 , 0.654 5 , 0.080 6 , 0) 同理可以得出事理、人理及综合评价测度矩阵分别为: (CRk)=(0.591 5 , 0.048 6 , 0.266 5 , 0.093 4 , 0) (CRk)=(0.145 5 , 0.175 6 , 0.491 3 , 0.187 5 , 0) (CWSRk)=(0.338 3 , 0.136 2 , 0.423 2 , 0.102 3 , 0) 该项目位于江苏昆山市,主要包括2幢仓储及门卫室,占地面积51 342.60m2,建筑面积约31 726m2。其中仓储厂房的面积均为15 831m2,大部层数1层,局部2层,层高4.5m,主要采用预制金属压型板单板墙体、叠合板以及钢框架,涵盖了劲性柱、方管、箱型柱以及楼层H型钢梁。 本案例数据获取方式、数据分析方法、组合权重计算、未确知测度评价计算均与前述装配式钢筋混凝土住宅项目一致。 在未确知测度理论中采用置信度识别准则来判断等级结果,设置信度λ=0.6,根据式(10),分别对各维度及综合评价等级区间进行确定。具体计算步骤,此处仅以“装配式钢筋混凝土住宅项目”为例作说明。 (1)物理维度下,当p0=2时,0+0.264 8=0.264 8<0.6,当p0=3时,0+0.264 8+0.654 5=0.919 4>0.6,因此可以判断物理维度下,该项目装配式建筑技术应用成熟度位于第Ⅲ级,即“发展级”。 (2)事理维度下,当p0=1时,0.591 5<0.6,当p0=2时,0.591 5+0.048 6=0.640 1>0.6,因此可以判断事理维度下,该项目装配式建筑技术应用成熟度位于第Ⅱ级,即“起步级”。 (3)人理维度下,当p0=2时,0.145 5+0.175 6=0.321 2<0.6,当p0=3时,0.145 5+0.175 6+0.491 3=0.812 5>0.6,因此可以判断人理维度下,该项目装配式建筑技术应用成熟度位于第Ⅲ级,即“发展级”。 (4)对于该项目装配式建筑技术应用综合评价,当p0=2时,0.338 3+0.136 2=0.474 5<0.6,当p0=3时,0.338 3+0.136 2+0.423 2=0.897 7>0.6,因此可以判断,该项目整体装配式建筑技术应用成熟度位于第Ⅲ级,即“发展级”。 通过采用置信度识别准则来判断等级结果,本文将两个案例进行了对比汇总,详见表6。 表6 各维度及综合评价等级 装配式钢筋混凝土住宅项目,根据事理维度数据可以看出,p0=2时,判断数据略大于0.6,由此可以判断事理维度也是整体具备进阶条件,因为个别指标评分较低,影响了该维度的成熟度等级。其中指标评分均值较最低且各专家对环境效益的认知差异较大,导致在客观权重计算时,所占权重较大,拉低了整体事理维度成熟度分值。侧面反映装配式建筑技术在应用及发展过程中,未能重视环境效益水平提升,若想提升该项目整体装配式技术应用水平,该处需要作为项目重点提升对象。 装配式钢结构厂房项目,根据物理维度数据可知,p0=5时,判断数据略大于0.6,由此判断物理维度跨入提升级,进一步判断装配式钢结构建筑的建筑技术已经得到全方面的发展和应用,到达高度统一化、集成化水平,进而预测未来可以在装配式建筑新型材料等领域进一步拓展和探索。 基于以上案例的结果分析,政府应加大装配式建筑产业发展的扶持力度,完善配套产业布局,加快编制并完善《装配式住宅设计选型标准》等指导文件,结合《钢结构住宅主要构件尺寸指南》,构建“1+3”标准化设计和生产体系,引导生产企业与设计单位、施工单位就构件和部品部件的常用尺寸进行协调统一,发挥标准化引领作用,提高装配式建筑设计、生产、施工效率,进一步推动全产链协同发展。 引入WSR方法论和能力成熟度模型,构建了基于19个评价指标的装配式建筑技术应用成熟度评价体系,并通过组合赋权及未确知测度理论对评价结果进行量化,确定成熟度等级。以装配式建筑项目(包括装配式钢筋混凝土住宅项目和装配式钢筋结构厂房项目)为例,对模型的合理性和适用性进行验算。结果表明,装配式钢筋混凝土住宅项目整体装配式技术应用成熟度为Ⅲ级,即“发展级”。装配式钢筋结构厂房项目整体装配式技术应用成熟度为Ⅳ级,即“成熟级”。通过对评价结果分析,可以有针对性的对地区或项目装配式建筑技术应用情况进行提升和改进,为快速提升地区装配式建筑产业发展提供参考依据。4.2 确定单指标未确知测度矩阵

4.3 确定多指标综合测度矩阵
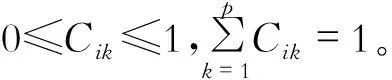
4.4 确定评价等级
5 案例分析
5.1 装配式钢筋混凝土住宅项目
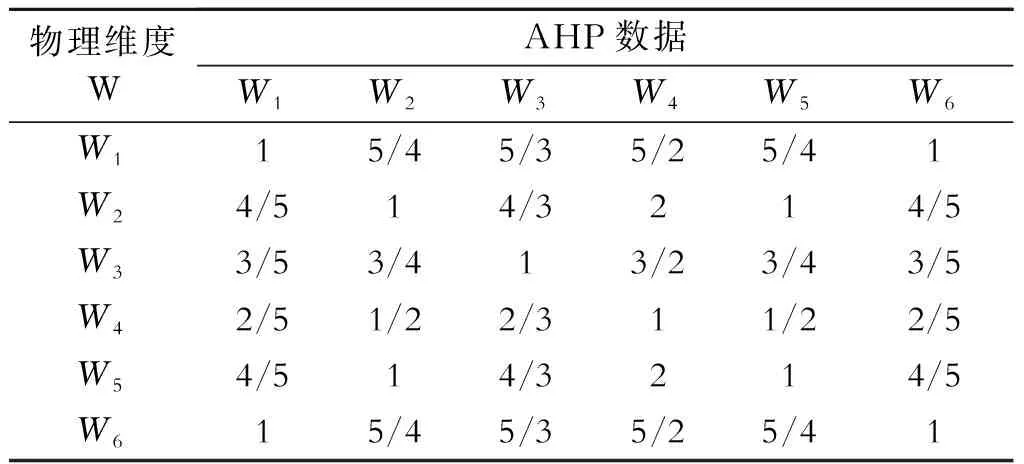
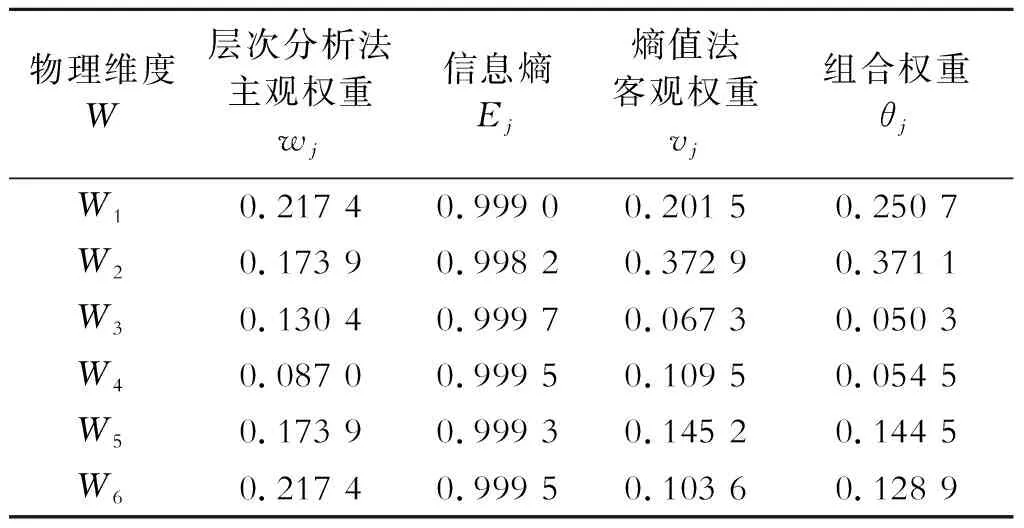
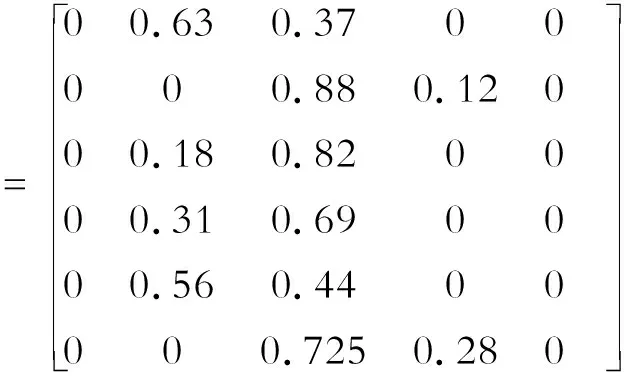
5.2 装配式钢结构厂房项目
5.3 评价等级的确定

5.4 结果分析及政策建议
6 结 语

