中压真空断路器操作机构反力特性匹配计算分析及应用
周 强
0 引 言
随着船舶电站容量的大幅增加,中压电力系统成为船舶电力系统新的发展方向。交流中压真空断路器是电能传输及分配至用电设备的重要元器件,通过上、下各级之间的选择性保护,实现整个电力系统供电的连续性,确保电力系统运行的稳定[1]。操作机构[2-4]是真空断路器关键的组成部分,其反力特性匹配曲线,决定了断路器能否顺利合闸以及合闸过程中的机械特性参数能否满足设计要求。
反力特性匹配曲线[5]主要是判断合闸过程中主轴所受的动力力矩与阻力力矩的关系。整个过程中如果动力力矩都大于阻力力矩,合闸就能够实现;如果动力力矩在某一位置或某一位置区间小于阻力力矩,合闸过程就有可能无法实现,需要在动、静触头接触之前,评估系统的动能是否足够克服阻力力矩的能量。如果具备足够能量,就可以依据惯性效应完成合闸操作。
以往操作机构反力特性的研究主要依靠设计人员的经验来设定机构参数大概范围,再通过大量试验找到合理的机构参数,设计周期长,研发效率低[6]。近年来随着计算机技术的发展,国内外主要利用ADAMS等仿真软件建立虚拟样机,模拟断路器操作机构的合闸过程来研究机构的反力特性[7-8]。也有部分学者通过解析和图解法相结合的方法,计算出分闸位置到合闸位置若干点的动力力矩和阻力力矩,然后利用MATLAB拟合得到整个过程的反力匹配特性曲线[9]。
本文以额定电压12 kV,额定短路电流40 kA的交流中压真空断路器操作机构为例,在理想状态下,不考虑摩擦力和重力的作用,从静态力学的角度来计算合闸过程每一时刻主轴所受动力力矩和阻力力矩的关系,并定量地研究了不同储能弹簧终拉力对反力特性匹配曲线的影响,为操作机构结构设计提供理论依据。
1 断路器操作机构原理
断路器操作机构为弹簧储能操动机构,主要由储能单元、储能弹簧、合闸单元、分闸弹簧、分闸单元和主轴等组成。储能弹簧通过储能电机、储能轴、链轮等储能单元储能完成后,通过储能保持掣子顶住滚轮保持在储能位置。在合闸操作中,储能弹簧释放的能量通过凸轮驱动四连杆机构带动绝缘拉杆和动触头进入合闸位置,并压缩触头弹簧,保持所需要的接触压力。断路器操作机构如图1所示。

图1 断路器操作机构
2 合闸过程中力矩计算
合闸传动机构主要由2个四连杆机构组成。为了后面方便叙述,两个四连杆机构分别命名为四连杆机构Ⅰ(连架杆1、传动杆P和连架杆2)和四连杆机构Ⅱ(连架杆3、传动杆Q和连架杆4),对于主轴来讲,连架杆2提供动力力矩,连架杆3提供阻力力矩。合闸传动机构示意图如图2所示。

图2 合闸传动机构示意图
根据实际设计的断路器三维模型各动作机构的实际位置,按照1∶1比例进行绘制,真空断路器操作机构合、分闸位置简图如图3所示。以该简图为基础计算反力特性匹配曲线。
2.1 主轴所受动力力矩的计算
合闸动力由两部分组成:储能弹簧力和真空灭弧室的自闭力。在整个合闸过程,主轴所受动力力矩主要是由储能弹簧释放产生的。储能弹簧释放过程中,储能轴上的凸轮通过四连杆机构将动力力矩传递到主轴上,使断路器合闸。在动、静触头接触之前,真空灭弧室的自闭力也能够提供合闸所需要的能量,一旦动、静触头接触,自闭力不再提供合闸动力。
2.1.1 储能弹簧对储能轴产生的转矩计算
设储能轴转动角度为θ。由图3可知,合闸过程中储能轴共转动170.2°。当0<θ<7°时,凸轮尚未与合闸滚轮接触;当7°≤θ≤112°时,凸轮接触合闸滚轮,压着滚轮向下运动并至合闸位置;当112°<θ≤158°时,保持在过压状态,使合闸保持掣子复位;当158°<θ≤170.2°时,凸轮继续转动,离开合闸滚轮,使得凸轮与合闸滚轮之间有适当的间隙。
设储能释放过程中弹簧的长度为b3,由余弦定理可知
(1)
式中:b1——储能轴中心到储能弹簧下端固定点的长度;
b2——储能轴中心到储能弹簧上端固定点的长度;
θ——储能轴转动角度;
θ0——储能完成状态时b1与b2所成角度。
设合闸过程中储能弹簧力为F1,因储能弹簧有2根,即
F1=2[F0-K1(b0-b3)]
(2)
式中:F0——每根储能弹簧完成储能时终拉力;
K1——储能弹簧刚度系数;
b0——储能弹簧储能完成后弹簧的长度。
设储能轴中心到弹簧的距离为b4,则
(3)
储能弹簧对储能轴产生的转矩M0为
M0=F1b4
(4)
2.1.2 主轴转动角度φ与储能轴转动角度θ的关系
设主轴转动角度为φ。合闸过程中,储能弹簧释放带动储能轴转动,此时储能轴上的凸轮通过四连杆机构推动主轴转动,因此主轴转过角度φ与储能轴转过角度θ有确定的一一对应关系。
在四连杆机构Ⅰ中,由三角形的余弦定理可得
(5)
设连架杆1转过的角度θ3,则
(6)
式中:c1——连架杆1的长度;
c2——传动杆P的长度;
c3——连架杆2的长度;
c4——连架杆1的支点到主轴中心的长度;
c5——四连杆机构Ⅰ对角线长度;
θ1——连架杆1与c4的初始角度;
牛哞悠长,挽篮入园,随心所欲采摘时鲜。拾级而上,山坡有亲子厨房。厂房车间式开放厨房,石垒砖砌灶台,铁锅劈柴烟囱,炊具一应俱全。可一试身手卖弄厨艺,亦可请教村夫农妇烹饪窍门。可见反客为主非诳语,此处可学故人邀诗人,把盏话桑麻。
θ2——连架杆2与c4的初始角度。
上面已经建立了连架杆1转动角度θ3与主轴转动角度φ的关系,现只需要建立连架杆1转动角度θ3与储能轴转动角度θ的关系,从而建立起主轴转动角度φ与储能轴转动角度θ的一一对应关系。
凸轮[10-11]由多段圆弧组成,在储能轴转动过程中,凸轮跟着同步转动。在不同时刻,凸轮与合闸滚轮接触的圆弧不一样,现以储能轴中心为坐标原点建立直角坐标系。连架杆1转动角度θ3与储能轴转动角度θ关系计算示意图如图4所示。
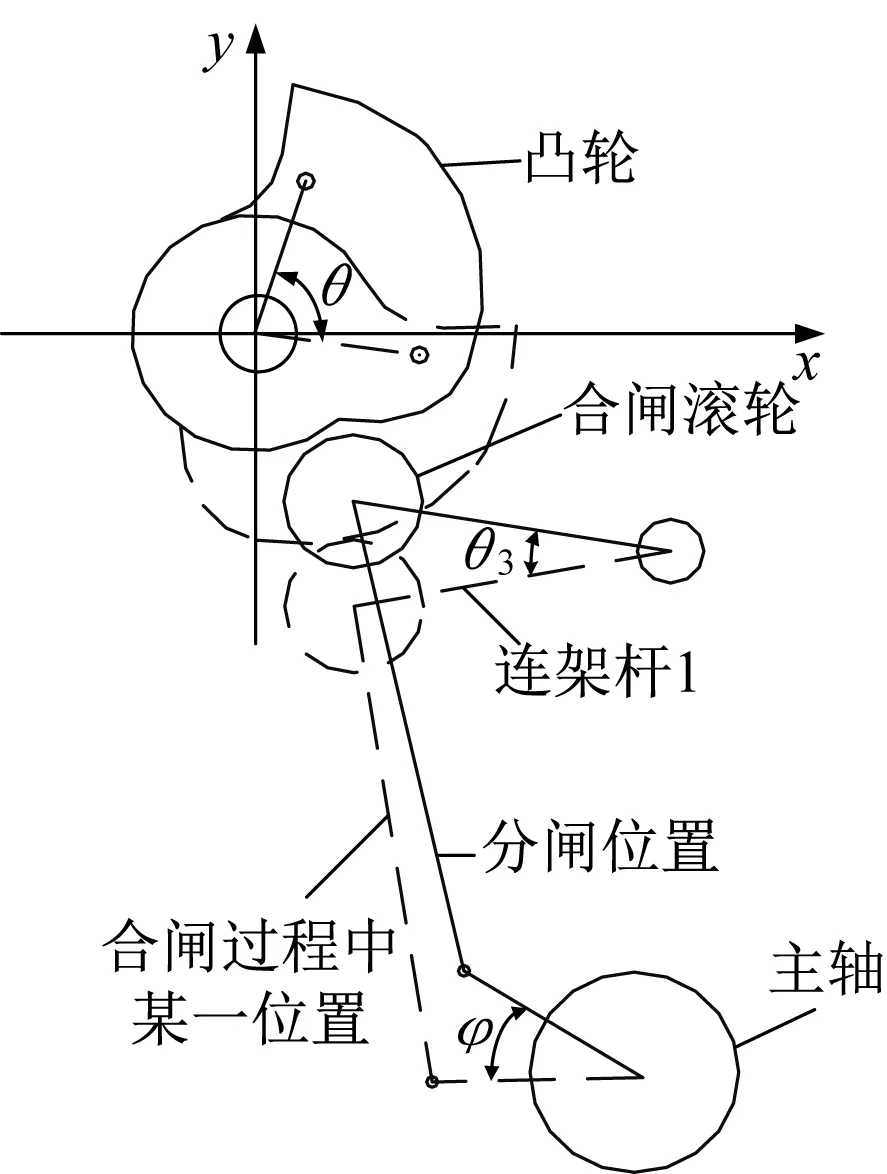
图4 连架杆1转动角度θ3与储能轴转动角度θ关系计算示意图
(7)
(8)
(9)
式中: (x1,y1)、(x2,y2)、(x3,y3)——储能状态完成时凸轮上第一段圆弧、第二段圆弧和第三段圆弧对应的圆心的坐标;
(x5,y5)、(x6,y6)、(x7,y7)——凸轮顺时针转动θ角度时第一段圆弧、第二段圆弧和第三段圆弧对应的圆心的坐标。
(10)
式中: (x0,y0)——连架杆1支点的坐标;
(x4,y4)——初始位置时连架杆1上合闸滚轮中心对应的坐标;
(x8,y8)——连架杆1逆时针转动θ3角度后合闸滚轮中心对应的坐标。
(11)
式中:r0——合闸滚轮的半径;
r1、r2、r3——凸轮上第一段圆弧、第二段圆弧和第三段圆弧对应的半径。
由式(11)可以建立连架杆1转动角度θ3与储能轴转动角度θ的关系,再联合式(6)就可以建立主轴转动角度φ与储能轴转动角度θ的一一对应关系。
2.1.3 储能弹簧对主轴产生的动力力矩计算
设储能轴中心到连架杆2端点的长度为c7,储能轴中心到连架杆1端点的长度为c8,则
(12)
(13)
式中:c6——储能轴中心到连架杆1支点的长度;
θ6——c6与连架杆1的初始角度。
设储能轴中心到传动杆P的距离为c9,则
(14)
传动杆P所受沿杆方向的作用力F2为
(15)
设四连杆机构Ⅰ中另一条对角线的长度为c10,则
c10=
(16)
设主轴中心到传动杆P的距离为c11,则
(17)
储能弹簧对主轴产生的动力力矩M1为
M1=F2c11
(18)
2.1.4 真空灭弧室自闭力对主轴产生的动力力矩计算
在真空灭弧室自闭力作用下,设传动杆Q所受沿杆方向的作用力为F4,则
(19)
式中:F3——真空灭弧室自闭力;
l1——与绝缘拉杆相连的拐臂到转动支点的长度;
a2——连架杆4的支点到传动杆Q的距离。
真空灭弧室自闭力对主轴产生的动力力矩M2为
M2=F4a3
(20)
式中:a3——主轴中心到传动杆Q的距离。
合闸过程中主轴所受动力力矩M3为
M3=M1+M2
(21)
2.2 主轴所受阻力力矩的计算
合闸反力也由两部分组成:分闸弹簧力和触头弹簧力。合闸过程中主轴共旋转39.5°,其中当主轴旋转角φ<23°时,动、静触头尚未接触,此时主轴所受阻力力矩仅由分闸弹簧产生;当旋转角23°≤φ≤39.5°时,动、静触头接触,进入超程阶段直至合闸结束,这个过程中主轴所受阻力力矩由分闸弹簧和触头弹簧共同产生。
2.2.1 分闸弹簧对主轴产生的阻力力矩计算
在四连杆机构Ⅱ中,利用三角形的余弦定理得
(22)
式中:l9——四连杆机构Ⅱ对角线的长度;
l4——与主轴相连的连架杆3的长度;
l8——主轴中心到连架杆4支点的长度;
α0——分闸状态时连架杆3与l8的初始角度;
φ——主轴旋转角度。
设连架杆4转过的角度为β1,则
(23)
式中:l2——连架杆4的长度;
l3——传动杆Q的长度;
α1——连架杆4与l8的初始角度。
设l10为分闸弹簧长度,F6为每根分闸弹簧力,则
(24)
F6=F5+K2(l10-l6)
(25)
式中:l5——分闸弹簧下端的连杆长度;
l7——分闸弹簧上端固定点到下端连杆支点的长度;
α2——l5与l7的初始角度;
l6——分闸弹簧初始安装长度;
F5——分闸弹簧初始力;
K2——分闸弹簧刚度系数。
设a1为分闸弹簧所对应的力臂长度,则
(26)
设a2为连架杆4的支点到传动杆Q的距离,则
(27)
设F7为传动杆Q所受的压力,则
(28)
设四连杆机构Ⅱ中另一条对角线的长度为l11,则
l11=
(29)
设a3为主轴中心到传动杆Q的距离,则
(30)
分闸弹簧总共有3根,故分闸弹簧对主轴产生的阻力力矩M4为
M4=3F7a3
(31)
2.2.2 触头弹簧对主轴产生的阻力力矩计算
真空断路器的超程为3.5 mm,设超程阶段每相触头弹簧力为F9,则
(32)
式中:F8——每相触头弹簧预压力;
K3——触头弹簧刚度系数;
l1——与绝缘拉杆相连的拐臂到转动支点的长度;
d——断路器的开距。
设F10为传动杆Q所受压力,则
(33)
触头弹簧对主轴产生的阻力力矩M5为
M5=3F10a3
(34)
合闸过程中主轴所受阻力力矩M6为
M6=M4+M5
(35)
3 结果分析
采用参数对断路器合闸过程中每一时刻动力力矩和阻力力矩进行理论计算。F0=1 135 N,c1=58 mm,c6=85.5 mm,K3=742.85 N/mm,K1=11.75 N/mm,c2=90.5 mm,θ6=19.4°,l1=80.4 mm,b0=278.1 mm,c3=38 mm,F3=350 N,l2=103.5 mm,b1=248.5 mm,c4=99.1 mm,F5=375.2 N,l3=53.3 mm,b2=30 mm,θ1=96.4°,F8=2 000 N,l4=38 mm,θ0=170.2°,θ2=61°,K2=17 N/mm,l5=62.6 mm,l6=125.2 mm,l8=127.3 mm,α1=34.5°,d=11 mm,l7=128.5 mm,α0=100.4°,α2=72.8°,x0=75,y0=-41,r0=12.5,x1=20.49,y1=8.28,r1=25.1 mm,x2=24.44,y2=-0.97,r2=15 mm,x3=0.58,y3=8.43,r3=40.7mm,x4=17.76,y4=-31.64。
用MATLAB软件编程求解出主轴所受动力力矩和阻力力矩随主轴转动角度的变化关系。主轴所受动力力矩与阻力力矩的关系如图5所示。
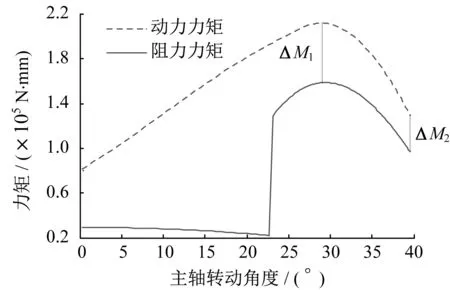
图5 主轴所受动力力矩与阻力力矩的关系
由图5可见,动力力矩在合闸开始后迅速增大,在动、静触头接触前,阻力力矩主要由反力弹簧产生,这个阶段阻力力矩基本平稳并且略有减小,这就意味着动力力矩与阻力力矩的差值不断增大,主轴的转动加速度不断增大,动触头的速度不断增加,以便提供合适的刚合速度;而当动、静触头接触后,阻力力矩发生突变,这是因为触头弹簧力的作用,但从图5看,阻力力矩还是小于动力力矩,之后阻力力矩和动力力矩几乎同时达到最高点然后减小,直至合闸结束。因此对于主轴来说,整个合闸过程中受到的动力力矩大于阻力力矩,能够满足合闸过程对于机构静态力的要求。实际样机做试验也证明这样的反力特性匹配曲线能够满足断路器的机械特性参数。
如果改变储能弹簧的终拉力F0,可以得到不同储能弹簧终拉力条件下反力特性匹配曲线,从而可以定量地分析不同参数对反力特性匹配曲线的影响。不同储能弹簧终拉力条件下反力特性匹配曲线如图6所示。由图6可知,当储能弹簧终拉力F0为600 N时,动、静触头接触后,动力力矩明显小于阻力力矩,则很有可能断路器不能顺利合闸;相反地,当储能弹簧终拉力F0为1 300 N时,最高点的动力力矩与阻力力矩差值ΔM3=89.0 N·m,比图5的最高点动力力矩与阻力力矩差值ΔM1=52.3 N·m增加了70.2%,合闸终了时的动力力矩与阻力力矩差值ΔM4=65.3 N·m比图5的ΔM2=32.7 N·m增加了99.7%,会导致合闸后剩余能量[12]太多,从而引起触头弹跳,这对整个操作机构的强度和寿命也有不利影响。
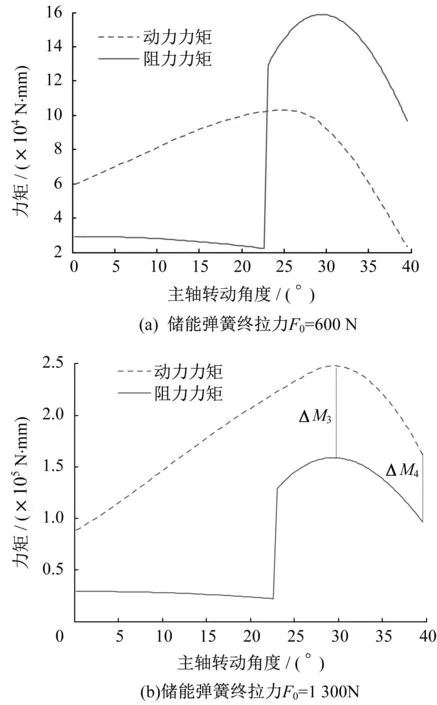
图6 不同储能弹簧终拉力条件下反力特性匹配曲线
因此储能弹簧的终拉力不能太小也不能太大,要通过理论计算的方法定量地设计合理的反力特性匹配曲线。同样也可以定量分析研究储能弹簧刚度系数、分闸弹簧初始力和刚度系数、触头弹簧初始力和刚度系数等参数对反力特性匹配曲线的影响,具有重要的指导意义和工程意义。
4 结 语
合闸操作是中压真空断路器重要的操作过程,力矩匹配设计不合理会导致断路器合闸难、合闸慢或机械寿命降低。本文阐述了一种中压真空断路器操作机构合闸过程中每一时刻主轴所受动力力矩和阻力力矩匹配关系的理论计算方法,并定量地研究了储能弹簧终拉力对反力特性匹配曲线的影响,对指导断路器操作机构中储能弹簧、分闸弹簧和触头弹簧等参数变量的设计和优化具有重要的工程意义。

