基于数字图像相关方法的Q235钢单轴拉伸变形研究
肖汉斌 陈 田 于家硕 裴雪冬 李占峰
1武汉理工大学交通与物流工程学院 武汉 430063 2大连港散杂货码头公司技术工程部 大连 116001
0 引言
起重机被广泛运用于港口运输、机械等行业,由于其部分金属构件长期处于复杂的载荷条件下,其故障的产生与金属结构的加工工艺、现场环境和作业工况有很大关系,故应力应变是反映金属故障的重要指标[1]。传统测量手段只能实现局部检测,难以得到构件的全场应变[2];而数字图像相关方法通过计算机视觉技术,对拍摄的图像进行识别处理及数值计算,从而获得检测对象的位移场以及应变场,避免了传统方法不能测量全场应变的弊端[3,4]。起重机的常用材料为Q235钢,通过数字图像相关方法对Q235钢的力学参数、应变测量进行研究有助于提高对起重机健康检测的针对性。
数字图像相关方法由日本的Yamaguchi I[5]、美国南卡大学的Peter W H等[6]分别在1981年、1982年各自独立提出;Zhao W Z等[7]在对火箭发动剂燃料的泊松比测量时运用了DIC方法;Lyons J S等[8]在1996年通过DIC方法实现了高温物体表面位移与变形的测量;2006年杨勇等[9]通过研制双CCD长距显微数字图像相关测量系统,构建了高精度数字图像相关测量系统;2007年潘兵等[10]为了从含有噪声的位移场中提取出准确可靠的应变场,提出了一种基于最小二乘法的全场应变求解方式;2009年Pankow M等[11]在对大离面位移进行测量时,运用了三维DIC方法 ;2013年,为了消除离面位移等不利因素对测量结果的影响,潘兵等[12]提出了使用双远心镜头进行高精度拍摄的方法;曹广龙等[13]通过 DIC 方法对铝合金焊接接头拉伸性能进行了研究,得到焊接区在拉伸时的连续屈服强度曲线。
对起重机金属构件进行准确可靠的应力应变检测对保证起重机结构安全有着重要的意义。本文按照标准规定方法,对起重机械用钢Q235钢标准试件进行单轴拉伸实验。采用应变片、DIC这2种方法对试件的应变场进行测量,并对比2种方法得出测量值。此外,利用拉伸试验机输出的数据作为仿真实验基础,通过Abaqus有限元分析软件进行仿真模拟,与DIC方法测得的位移场、应变场进行对比。通过对比几种方法的测量数据,验证DIC方法的准确性以及通用性,为DIC方法在对起重机金属构件安全检测中提供一定的参考。
1 数字图像相关方法概述
1.1 基本原理
数字图像相关方法是通过计算机视觉技术来进行图像的处理以及数值计算的测量方法。它分析计算的对象是在变形前与变形后拍摄的2幅图像,一般将变形前拍摄的图像称为参考图像,将变形后拍摄的图像称为变形图像。在DIC方法的常规实现过程中,先在参考图像中选取一个感兴趣区域(ROI),然后将ROI区域划分成间隔均匀的虚拟网格,计算网格中的每一个点得出相应的位移,从而获得全场变形。其基本原理是:跟踪(或匹配)在变形前后拍摄的2幅图像中的相同像素点(见图1),为了成功计算点P(x0,y0)的位移,选择参考图像中以点P为中心,大小为(2M+1)×(2M+1)像素组成的正方形参考子区,用于匹配在变形图像中点P的对应位置。之所以选择矩形区域作为图像子区进行匹配,是因为矩形子区能包含的图像灰度变化更宽,识别更准确。

图1 参考子区与目标子区
为了能定量评估参考图像子区与变形后的图像子区的相似度,必须设立一个互相关准则作为目标函数,整个匹配过程就是寻找相关函数的峰值。当检测到相关函数的极值时,即可确定变形图像中子区的位置。计算参考图像中图像子区中心与变形子区中心位置的变化,即可得出P(x0,y0)的位移变化信息。
目标子区在变形的过程中,不仅点的位置会发生移动,整个目标子区的形状也有可能发生变化。因此,可以根据所谓的形函数或位移映射函数,将点P(x0,y0)周围的点Q(xi,yi)的坐标映射到目标子区中的点Q(xi′,yi′),即

若在变形过程中只存在刚体平移,则可使用零阶形函数,即

当子区的形状改变为平移、旋转、拉伸、剪切及其组合时,可使用一阶形函数进行描述,即

式中:u、v为参考子区的中心点在x、y方向的位移分量,ux、uy、vx、vy分别为参考子区的一阶位移梯度。
由式(1)~式(3)可知,面内变形可由子区中心点的位移及其4个位移梯度进行描述。
1.2 相关函数
为了定量评估参考子区与目标子区之间的相似度或差异度,必须采用相关函数来计算相关系数。文献[14]总结了几种常见的相关函数,并对各函数进行了定量分析。由于零均值归一化的互相关函数Zncc与零均值归一化的差值平方和函数Znssd对变形子区的比例和位移变化不敏感,其抗干扰能力优于其他函数,故最为常用。零均值归一化的互相关函数可表示为

式中:fm、gm分别为参考子区和目标子区的平均灰度值,f(xi,yi)为参考子区中点(xi,yi)的灰度值,g(xi′,yi′)为目标子区中点(xi′,yi′)的灰度值。
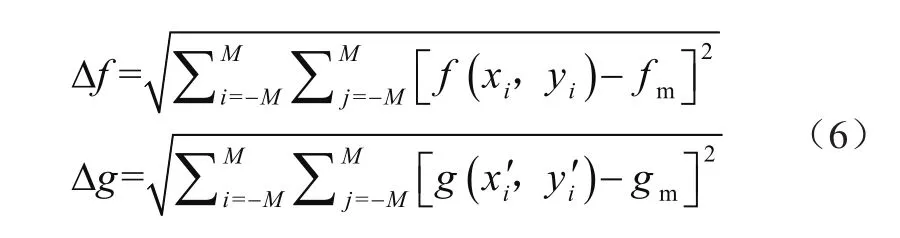
Δf、Δg的定义为CZncc的取值范围为[-1,1],当其为最大值时,参考子区与目标子区的匹配程度最高;CZnssd的取值范围为[0,4],当其为最小值时,参考子区与目标子区的匹配程度最高。
1.3 亚像素位移计算算法
在物体的变形过程中,变形子区中的坐标点可以介于亚像素位置,为了提高测量整体的精度,有必要使用亚像素级别的位移计算算法。目前最常用的亚像素算法有N-R算法、曲面拟合法、梯度算法等,其中N-R算法的测量结果更精确、更稳定,故N-R算法是目前最常用的亚像素位移计算方法[15]。
挂袋后催芽管理应坚持保湿为主、通风为辅,空气相对湿度85%以上,即袋表面有露水但不滴落为宜。保湿方法可将地面浇透水,每天喷几次雾状水,喷水量不宜过大,防止刺孔处进水感染杂菌和青苔。每天早、晚各通风1小时,根据气温变化在大棚上适当增减覆盖物,防止冻害发生,管理得当7~10天天即可出齐耳芽。当棚内温度超过25℃以上时,应采取通风或遮荫等方式降温。
当将参考子区与目标子区之间的相对变形考虑在内时,关联函数即变为映射参数向量的非线性函数。在一阶形函数中,映射参数向量应为p=(u,ux,uy,v,vx,vy)T。在N-R算法中,目标子区被W(ξ;p)变形,其中,p0为变形的初始猜测值,是迭代的初始值;p为迭代后的变形参数;W(ξ;p)为位移映射函数,它描绘了目标子区相对于参考子区的位置与形状。然后,将一个增量参数向量Δp应用于变形子区,根据给定的关联准则,与原始参考子区进行比较求解Δp,图2为N-R算法匹配策略示意图。
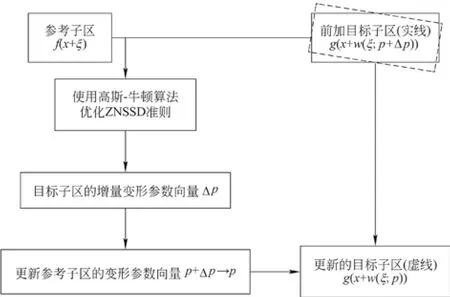
图2 N-R算法匹配策略示意图
为了定量评估参考子区与目标子区之间的相似性并确定变形参数,本文决定采用鲁棒的Znssd准则。在采用Znssd函数时,当相关函数CZnssd(p)取最小值,相关函数的梯度趋近于0时,即有


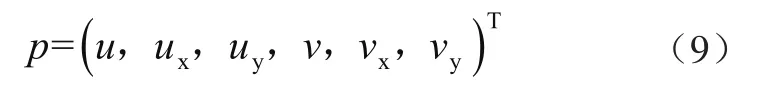
式(7)可用Newton-Raphson迭代法来求解,得到

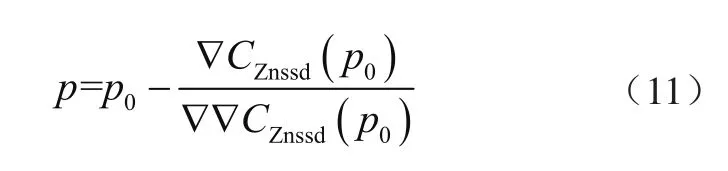
式中:p0为变形的初始猜测值,p为迭代后的变形参数,ΔCZnssd(p0)为相关函数的梯度值,ΔΔCZnssd(p0)为相关函数的二次偏导,一般将ΔCZnssd(p0)称为海森矩阵。
若要获得准确的变形参数p,首先要得到变形初值p0。一种简单的搜索方法为整像素位移相关搜索方式,但其得到的变形初值却难以表达图像的旋转等信息,后续迭代次数较多。因此,选用一种计算量小且能很好表达物体变形情况的估计手段,人机交互方式来进行初值的估计。
1.4 亚像素插值手段
在式(7)中,坐标(xi′,yi′)的灰度值可能会是亚像素级别的坐标位置的灰度值,需要使用亚像素强度插值算法,其中最常用的一种插值方法为双三次插值算法,具体操作如图3所示
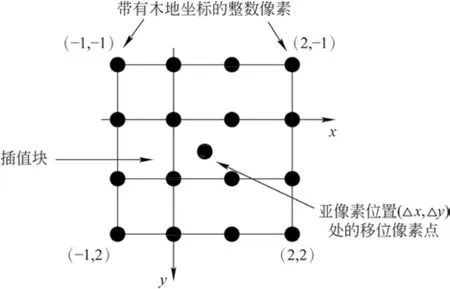
图3 双三次插值示意图
在使用双三次插值方案时,亚像素位置的灰度值和一阶灰度梯度可表示为

式中:g(Δx,Δy)为插值函数,gx(Δx,Δy)、gy(Δx,Δy)为插值函数的一阶导数,Δx、Δy为亚像素插值点与已知点(m,n)之间的距离。
1.5 应变测量手段
利用上述算法能以亚像素精度得到全场位移,但在结构应力安全分析中,全场应变分布是更重要的结果。就数学理论而言,应变与位移之间的关系是一个数值微分的过程,但在对N-R算法得出的位移数据进行微分过程时会放大位移数据中包含的噪声,通过这种方式得出的应变亦并非可靠。因此,对于应变场的估计,更有效的技术为文献[10]中提到的逐点局部最小二乘法拟合。
为了计算点(x,y)的应变,首先要选择一个(2N+1)•(2N+1)的应变计算窗口。应变计算窗口的实际大小为(2N•ΔL)2个像素,ΔL为相邻点之间的网格步长。当划分的应变计算窗口较小时,其内部的局部位移分部可被近似表达为

式中:(i,j)为应变计算窗口内的本地坐标;u(x+i,y+i)、v(x+i,y+i)为通过DIC方法获得的原始位移;a0、a1、a2、a3、b0、b1、b2、b3为待确定的多项式系数。
可通过最小化式(14)中的2个目标函数来预估以上系数,即有


式中:εx为横向应变,εy为纵向应变,εxy为切向应变。
一旦获得这些系数,即可计算出应变窗口区域中心点处的应变。对所有的待求点逐点进行局部最小二乘拟合,再用上述方法对所有待求点进行计算,即可获得全场应变。
基于上述DIC原理,采用Matlab编写DIC程序,实现对变形前后图像的分析与数值计算,从而获得目标区域的位移应变数据。
2 单轴拉伸实验
2.1 实验试件设计
实验试件采用3块Q235钢材试件,应变片粘贴位置为试件中心位置下方20 mm处。试件几何形状与应变片粘贴位置如图4所示。
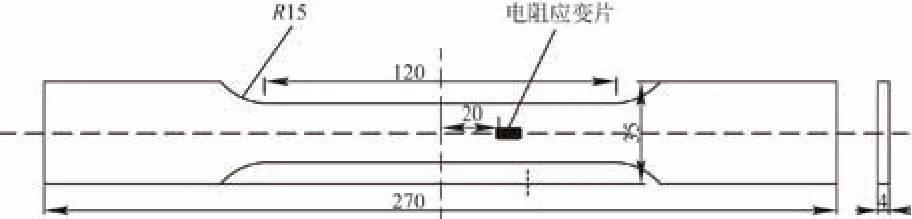
图4 实验试件形状尺寸以及应变片粘贴位置示意
2.2 实验过程
在进行实验前,被测物体表面需要有分布随机均匀且对比度高的散斑场,散斑场的制备可通过在试件表面分别喷涂黑白哑光漆来制作,制作完成的散斑场如图5所示。为了保证实验的可靠性以及可重复性,将3个试件记为Q-1、Q-2、Q-3分组进行单轴拉伸实验。实验以位移控制的方式进行加载,位移速度为2 mm/min,通过DIC、应变片2种方式完成位移、应变的测量。在实验装置中,将制备好散斑场的试件竖直的固定在拉伸试验机上,确保应变片粘贴位置在相机取景框中,在实验过程中,保持相机镜头光轴与实验试件的表面保证垂直。

图5 带散斑的未拉伸试件
本实验采用WDW-50E 微机控制电子式万能试验机,照片尺寸为422 pixel×645 pixel。实验共采集1张未加载时的图片、15张不同载荷下的变形图片,这15张照片每张的间隔为10 s。
3 有限元仿真实验
3.1 仿真模型构建以及载荷确定
以拉伸试件为研究对象,在有限元软件Abaqus中对本实验进行仿真模拟。试件上端设置完全固定,在实验试件下端设置加载点;仿真模型中的各项力学参数与试件一致。对试件下端施加载荷,具体数据由实验装置的拉伸试验机输出的位移时间曲线确定。
3.2 有限元模型网格划分
图6为实验试件划分的有限元网格。由于试件自身的形态、加载方式等因素的影响,主要的位移应变会出现在试件的标距段。因此,对整个试件进行网格划分后,对标距段进行进一步的网格细分,从而得到更准确的仿真数据。网格过度良好,无畸变存在,网格类型为C3D8。网格单元总数为8 924。
4 实验结果与分析
在ROI区域确定后,选取图像子区大小为35 pixel,选择的搜索步长为2 pixel。图7为DIC方法测得3组试件ROI位置的时间-位移曲线,从图中可以看到3次实验具有的稳定性以及可重复性,故选用其中一组Q-2进行分析对比。之后进行应变计算,应变计算窗口的大小为25 pixel。图8为150 s时通过DIC方法测得的标距段应变场数据。从图中可以看出,通过DIC方法测得的应变场有微弱的噪声影响,其原因是镜头本身的热效应以及光照不均匀所带来的微小噪声。

图8 150 s时通过有测得试件表面应变场
为了验证DIC方法的准确性,将通过仿真模拟得出的位移数据与DIC方法得出的位移数据进行比较,如图9所示。同时,将应变片测量值、通过有限元仿真得出的模拟值、DIC分析值进行比较,如图10所示。由图9可知,在实验最开始阶段位移的变化很小,2种方法几乎没有差别;随着实验的进行,2种方法得到的位移数据出现差值,但两者的相对误差仍控制在5%以内,随着载荷持续增加,两者之间的相对误差在逐渐减小。由图10可知,DIC方法分析值与应变片的测量值之间有着微小的误差值,两者的相对误差最大不超过5%,并随实验的进一步进行,两者的相对误差逐步缩小,且与仿真模型所计算的应变数据接近吻合。

图9 试样Q-2 DIC方法测量值与有限元仿真对比

图10 试样Q-2 DIC方法测量值、应变片测量值与有限元仿真对比
通过DIC得到的分析值与应变片测量值之间的误差产生的因素有:在测量时试件发生振动,产生离面位移;相机镜头自热产生的镜头畸变;试件表面的光照强度产生变化。离面位移会改变物体与镜头之间的距离,使物体表面接近或远离成像面,从而导致虚假应变的产生。相机通电后会不可避免地产生自热,这些自热与环境温度的变化导致相机传感器的位置发生变化,从而影响了成像。光照环境的改变会影响到数字图像的灰度值,从而产生噪声。
5 结论
1)通过DIC方法与有限元软件模拟可获得Q235钢在拉伸实验中的位移变化,且两者的数据基本一致,证明了DIC方法在金属拉伸变形研究中位移场测量的可靠性;
2)通过应变片获取的Q235钢变形过程应变测量值与DIC方法获取的分析值相对误差控制在5%以内,证明了DIC方法在测量Q235钢应变值时的可靠性。为DIC方法在起重机金属构件安全检测中提供了有力的参考。

