一种基于语义推理的网络社区发现模型

任薇，阮淇昱，韩孟凯，邱玉辉

1. 西南大学 计算机与信息科学学院 软件学院， 重庆 400715； 2. 西南大学 人工智能学院， 重庆 400715

社区发现(Community Discovery)是将复杂网络拓扑结构分解为有意义的节点集群的任务[1]． 目前主流的社区发现方法基于聚类计算， 通过无监督学习训练发现共同群体[2-3]． 然而， 由于现有网络节点属性不同， 对于社区的定义各种各样， 聚类结果带有一定的随机性， 不能实现精准分类[4]． 另一方面， 现有划分算法只关注平面数据， 没有充分利用个体和链接属性信息的语义， 导致划分不准确[5-6]． 同时， 当前社区发现算法主要通过将有向图转化为无向图来进行社区发现， 此过程可能丢失很多细节导致社区结果划分不准确． 为实现对节点关系的准确描述， 在社区网络中加入有向性[7]， 通过描述不同种类的链接， 可以更真实模拟社交网络等现实世界网络．

Satuluri算法[8]与LSW-OCD算法[9]都是根据节点的矢量将有向图转化为带方向权值的无向图， 虽然Satuluri算法的复杂度已经在LSW-OCD得到较大改善， 但节点中隐含着的语义与语义的关系却没有在算法中发挥作用． 语义研究不仅关注事物概念的含义， 还关注含义间的关系． 在社会网络中， 用户的行为都与用户本身的特征、 爱好、 习惯等紧密相连． 社区发现中语义的引入， 为挖掘非数据信息提供了可能， 从而支持对网络社区更精确地划分． 基于语义对社区发现的应用潜力， 本文提出以语义推理为基础的网络社区发现模型．

1 语义网络及语义搜索

语义网络是当前万维网的扩展． 在语义网络中， 信息被赋予了明确的含义， 使计算机和人能够更好合作[10]． 语义网络中的概念节点按照层次进行组织， 可以表现每个层次中不同节点之间的平面关系以及不同层次中节点的纵向关系[11]．

语义搜索是语义网络的核心[12-14]． 语义搜索过程依据对本体处理原理的差异， 可以分为3种： 增强型语义搜索、 知识型语义搜索及其他搜索． 我们提出基于语义关系的发现模型， 通过关注节点间的语义特性[相等(Equal)、 相似(Similar)、 引用(Reference)、 序列(Sequence)、 子类(Subclass)、 蕴含(Implication)]， 采用语义链进行增强型推理， 期望得到更贴近真实情况的社区发现结果．

2 基于语义关系推理的立体社区发现模型

人类的社交网络与其他网络不同， 具有语义性， 基于语义推理的社区发现更贴合真实情况． 在社区结构划分的研究中， 研究者主要关注两方面问题： 一是社区的边界性， 即社区边界必须是封闭的； 二是社区的内部紧密性， 即一个拓扑结构即使看上去有封闭的边界， 但如果内部无紧密连接， 也不能认定为社区． 本文用总权值度量的方法衡量封闭性， 用节点相似度来考察社区的紧密性． 社区内部节点相似度的平均值通常大于社区间的相似度平均值． 因此， 本文给出社区结构定义如下：

给定一个混合图G， 将G划分为n个子图G1，G2，…，Gn， 使得任一子图Gi满足下列条件， 则Gi为网络G中的一个社区：

1) 对任意的节点N，din(N)是节点v在Gi中的度(权值)，dout(N)是节点v与除Gi外的其他子图间的连接的总度， 则对于其他子图Gj， 都有dout(N)-din(N)≤0；

图1 语义网络立体空间模型

2)Ni的内部节点平均相似度大于其与其他子图间的节点平均相似度．

以上定义的社区结构涵盖了不同尺度的社区．

2.1 多层模型及社区发现模型

本文提出一种基于语义的网络社区发现、 资源追踪的立体空间模型， 在传统的平面二维网络模型基础上， 针对语义网络节点间语义关系的特性， 提出三维的空间立体模型(图1)． 该立体空间模型将传统意义上的网络结构按语义关系类型重新构建， 模型拓扑结构分为纵面树拓扑结构(图2a)和平面图拓扑结构(图2b)．

模型采用立体空间节点拓扑结构， 利用节点语义及语义关系进行集成． 平面图中和纵面树中的语义节点， 其相互关系只能是特定的语义链中的一种或几种． 同时， 为了减少语义模糊性， 计算节点相似度后， 将相似度高的节点进行合并． 使得语义查询和社区发现可以快速转换到合适的语义平面上， 从而可以提高搜索的速度和查全率．

图2 语义关系拓扑结构

2.2 模型描述

本文根据语义链的特性构造空间立体语义链网络模型．

2.2.1 相等、 引用与序列

在平面上， 用有向图表示各节点间的关系． 定义空间模型中， 第n个平面上的图为Gn=〈Vn，Equn，Refn，Seqn〉， 其中：Vn是第n个平面上所有点的集合，Equn代表第n个平面图中所有语义链类型为 “相等”的节点集合，Refn与Seqn同理．

若多个节点间的语义链是相等的， 则合并所有的有此语义链关系的点为一点． 如图3网络中节点A，B，C间有“相等”语义链， 则合并为A(一般按第一个节点进行合并)， 节点D与B间语义链为其他类型， 则保留， 最后合并为两个节点A和D． “相等”语义链及合并结果见图3．

图3 “相等”语义链及合并结果

假设两节点A，B的语义相似度为α， 当α≥0.5时， 将此语义链的类型归入相等， 若α<0.5时， 则认为A，B语义不相关．

Ref为图中所有语义链类型为“引用”的节点关系集合，Refn=〈rn1，rn2…rnm〉，rni为第n个平面上第i条“引用”语义链．Seq是所有语义链类型为“序列”的节点集合，Seqn=〈sn1，sn2…rnm〉，sni为第i个序列． “引用”语义链和“序列”语义链的表示见图4．

“引用”语义链与“序列”语义链属于不同类型． “引用”语义链具有很强的时序性， 时间上， 要求前面的节点不能引用后面的节点．

2.2.2 蕴涵与子类

每个以树为单位的纵面搜索是从根节点语义(Root Semantics)开始， 以蕴涵或子类语义链作为搜索路径连接起来的各点． 路径上的节点具有一定的有序性， 且可以通过一个节点查找到其他节点． 蕴涵或子类可以表示为这样的树的集合． 纵面上的树结构可以表示为语义节点、 “子类”语义链、 “蕴涵”语义链的集合，T=(Vn，Sub，Imp)． “子类”语义链和“蕴含”语义链的表示见图5．

图4 “引用”语义链和“序列”语义链

“子类”语义链表示为Sub=∩〈Ni， …，Nn〉， 其中〈Ni， …，Nn〉是由节点Ni到Nn的一条“子类”语义链． 按定义， “子类”语义链有传递关系． 而“蕴涵”通常情况下并不单纯指简单的包含关系． 我们重点关注语义链关系， 即在某条或某几条语义链存在的情况下， 是否有某种特殊的且研究者感兴趣的语义链产生．

根据节点对象间相似度的度量和修正需要， 结合文献[11]中语义链关系定义及本文中社区发现定义， 提出语义推理表(表1)．

其中：Imp=∩〈Ni， …，Nn〉表示可能产生推理的各个语义节点集合，Equ代表相等关系，Sim代表相似关系，Ref代表引用关系，Sub代表子类关系，Non代表无关系．

2.2.3 相似度计算

用一个词空间的向量Vector(e)表示本文中的一个实体e， 每个维度对应一个词， 维度大小取值表明了这个词在刻画e时的相对重要性． 用词空间中的向量Vector(q)表示一条基于关键词的查询q．e和q的相似程度可以被描述为Vector(e)和Vector(q)的夹角余弦值．

语义结构的相似度取决于两个基本的要素： ① 语义节点组成社区的叶子结点， 且查询也是由叶子结点构成， 所以与社区的语义结构相关； ② 节点的祖先节点的相似程度．

表2给出了实现相似度算法所调用函数及其注释．

表2 函数及其注释

Ni与Nj语义结构相似度计算如下：

算法1Semantic-Structure-Similarity-Degrees (Ni，Nj)

IFNi属于社区中某一个最大语义群

THEN

T=Max-Semantic-Clique (Ni，Nj)

ELSE

T=Min-Common-Sub-Tree (Ni，Nj)

END IF

RootSetNi=T

NodeSet={Ni， …， Root (Ni)}∪RootSetNi

IF Length (Ni，Nj)=1

THEN

Semantic-Structure-Similarity-Degrees (Ni，Nj)=Semantic-Node-Similarity-Degrees (Ni，Nj)

Return()

ELSE

FORNkIN NodeSet

IFNk=Nj

ELSE IFNkIN RootSetNj

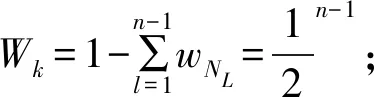
ELSE IFNk≠Nj

END IF

得到节点的相似度向量后， 还需要得到节点的权重向量，WNk则表示节点Ni与节点之间的重要程度．

算法2基于算法1， 在用户自定义权重W的影响下， 输出集合Setnm中的各个节点与Ni节点的语义结构相似度组成的向量．

算法2Semantic-Structure-Similarity-Degrees-extend (Ni， NodeSet)

NodeSetnm={Nn， …，Nm}

FOR (Njin NodeSet)：

Similarity-DegreesNj=Semantic-Structure-Similarity-Degrees(Ni，Nj)

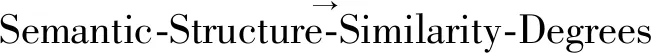
2.2.4 语义链网络立体空间构建

算法3描述语义链网络空间模型的构建．

算法3构建语义链网络立体空间模型(DataSet)

Filter(DataSet)； //网页抓取的数据通过本体集合过滤

Set_data=Init(DataSet)； //初始化输入集合Set_data

T，G=Trans(Set_data) //采用本体之间的关系遍历整个社区集， 确定一部分节点的Vn，Equ，Ref，Seq，Sub，Imp， 使用推理表格遍历已构造的图谱， 加速节点间关系的收敛．

M=Construct(G，T) //将用户的ID作为主体主键， 通过Semantic-Structure-Similarity-Degrees-extend算法构造空间立体模型M=(G，T)， 其中G=〈Vn，Eqa，Ref，Seq〉，T=(Vn，Sub，Imp)；

NodeSim=Norm(M.SimVec) //归一化各节点语义结构相似度

Sort(NodeSim{NSim1， …，NSimn}) //对其进行排序

Mark=0 //标记已被计算的节点(矩阵)为0

IFNSimi==1

THEN FORNiinG.EqaSetorT.SubSet∈NSimi

Ni⊂OutPut

Mark[i]=1

ELSEIFNSimi=<0.2

THEN FORNiinT.SubSetorG.EqaSet∈NSimi

Ni⊄OutPut

Mark[i]=1

FORMark[i]==0 andSimNi>0.5 //节点间关联度对相似度的修正

ImportantNi=1

ImportantNj=0.8

FORNjinImpSet

ImportantNj=ImportantNj+SimNi*(1-α)ImportantNi

FORNjinSeqSet

ImportantNj=ImportantNj+SimNi* (1-β)ImportantNi

FORNjinRefSet

ImportantNj=ImportantNj+SimNi* (1-γ)ImportantNi

FORMark[j]==0

SimNj=Important*SimNj

IFSimNj>0.5

Nj⊂OutPut

Mark[j]=1

Return qutPut

3 实验及分析

在本实验中， 我们通过模拟实验验证社区发现算法的准确性． 通过选取Facebook中的样本随机建立二层社交网络． 通过语义推理得到稠密矩阵， 并转化为无向图， 再对无向图进行社区划分证明本算法的有效性． 然后， 选取主流的社区发现算法K-means和隐语义模型(latent factor model， LFM)作为本模型算法的对比算法， 进行对比实验． 结果发现， K-means的社区划分准确性比其他两个算法更低， LFM和本文算法的社区划分准确度近似， 但当社区大小增长到1 000过后， 本文算法的模块度逐渐显示出优势． 模块度是衡量社区划分的强度指标， 以模块度值的大小来评价社区划分的优劣， 模块度值越接近1， 表示对社区结构的划分越好． 模块度值越大， 社区内部连接越紧密， 社区间连接越稀疏， 划分效果越好[1]．

实验采用斯坦福大学提供的ego-Facebook的数据集． ego-Facebook数据集是从App端采集的Facebook用户的数据， 包含了用户的属性、 社交圈(Circles)和ego network， 数据已被做了脱敏处理． 数据共有4 039个用户和88 234条连边． 其社交网络图的密度是0.005 409 92， 图直径为17， 平均距离为4.337 746， 能够很好代表现实世界中的好友关系．

本文实验在CPU为AMD Ryzen 7 5800Hz， 内存为16GB， 系统为Win10的电脑上运行．

3.1 社区发现模型的实验结果和分析

3.1.1 社区发现模型有效性

为了证明本文提出的社区发现模型的有效性， 本文先随机选取ego-Facebook中的一个用户， 建立两层社交网络关系图， 图中包含252个节与4875条边． 本文构造原始的不带权有向图， 推理得到稠密矩阵， 此时的边数为10 376， 包含了所有的语义关系． 本文将稠密矩阵作为相似度计算的输入得到无向图． 本文对无向图中的社区节点进行划分得到社区发现结果． 图6给出了原始的Facebook好友有向图、 转化的Facebook好友有向图、 Facebook好友无向图、 Facebook好友社区发现结果．

图6 基于Facebook的社区发现步骤及结果

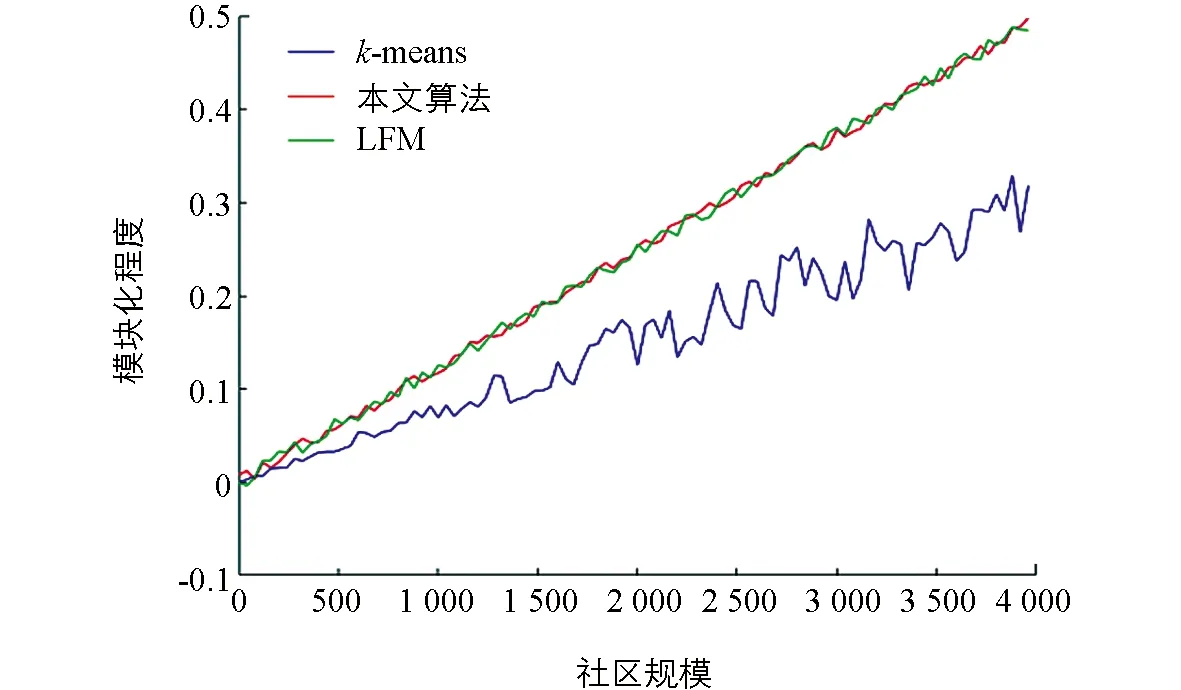
图7 算法对比

3.1.2 算法性能对比

我们选取社区发现主流的k-means算法和隐语义模型作为本模型算法的对比算法． 实验中， 从0个节点开始， 每次从数据库中随机取出40个新的Facebook用户节点添加到原有的网络中． 通过模拟发现， 3个算法在拟合下都是线性增长． 随着网络节点的增加，k-means算法对社区的划分结果不稳定， 呈现大幅波动状态． 3种算法对比结果见图7．

LFM和本文结果在社区划分结果方面差不多， 但当社区大小增长到1 000过后， 本文算法的模块化程度逐渐显示出优势．

稳定性方面， 如图8， 本文算法模块化方差为5.267 942e-06低于LFM算法模块化方差5.814 608e-06， 由此可见本文的算法更加稳定．

图8 本文算法与LFM算法个人circle结果比较

4 结论

本文提出基于语义推理的网络社区发现模型， 创新地从语义网络的角度， 探讨网络社区的构成及分割． 模型基于语义的平面和纵面两种特性， 利用图加树的空间拓扑结构， 进行基于语义推理的社区发现． 同时， 本模型通过语义本身特性， 将基于语义链的搜索简化到了层次范畴． 实验结果显示， 在模块度的评价指标下， 本文提出的模型对社区划分结果优于LFW和k-means算法． 另一方面， 由于语义的分割及关系的复杂性会影响本模型速度， 期望在下一步的研究中解决该问题．