基于“四问驱动”的“空间向量基本定理”的教学实录与反思*
周德春
(江苏省射阳中学 224300)
1 基本情况
授课对象 学生来自四星级省重点高中普通班,基础良好.
教材分析 “空间向量基本定理”是《普通高中课程标准实验教科书·数学(选修2-1)》(苏教版)第3章“空间向量与立体几何”中的第1节“空间向量及其运算”的第3小节内容,是空间向量线性表示、坐标表示的基础,是向量法解决立体几何问题的重要工具,是本章的核心知识点之一.
设计思想 在学习了平面向量基本定理的基础上,基于类比思想来研究空间向量基本定理.由于从平面到空间需要空间想象能力作为支撑,对于空间想象能力薄弱的部分学生学习起来还是有困难的,故在此教学设计中采取了“合作探究”的教学方法和“四问驱动”的教学范式,突出启发式教学、突出问题引领、突出数形结合、突出类比过程,以实现对空间向量基本定理的全面理解、猜想证明和简单运用.
教学目标 (1)运用类比的方法理解空间向量基本定理及其推论,体会空间任意一个向量可以用不共面的三个已知向量线性表示,而且这种表示是惟一的;(2)了解空间中基底的含义,并在简单问题中能用给出的一个基底来表示已知向量,初步感悟向量是研究几何问题的工具;(3)提升数学抽象、逻辑推理、数学运算、直观想象素养.
教学重点 空间向量基本定理的理解.
教学难点 空间向量基本定理的证明.
2 过程设计
2.1 问题情境
师:在数学中,我们常用类比法研究数学问题,比如类比集合来研究向量,类比指数函数来研究对数函数,类比椭圆来研究双曲线等.今天将类比平面向量基本定理来研究空间向量基本定理.(点题:空间向量基本定理)
2.2 探究建构
●通过类比得到的空间向量基本定理的内容是什么?如何证明这个定理?这个定理有什么用处?
说明
前面标注●的问题称为“启问”.所谓启问就是依据教学目标,提出问题.问题1
如何通过类比得到空间向量基本定理的?师:请问同学们,平面向量基本定理的内容是什么?
生:如果,是同一平面内两个不共线的向量,那么对于这一平面内的任一向量,存在惟一的有序实数对(x
,y
),使=x
+y
.师:定理中有哪些关键词?
生:平面内,,不共线,任一向量,存在,惟一.师:类比平面向量基本定理,结合关键词,请猜想出空间向量基本定理的具体内容.
生:平面内→空间中;,不共线→,,不共面;任一向量→任一向量,存在惟一→存在惟一,(x
,y
)→(x
,y
,z
),=x
+y
→=x
+y
+z
.(在学生回答的基础上给出下面的定理)
空间向量基本定理 如果三个向量,,不共面
,那么对于空间任一向量
,存在惟一
的有序实数组(x
,y
,z
),使=x
+y
+z
.(用着重号标出关键词)追问 猜想出来的结论可靠吗?
生:不可靠!需要证明.
师:证明的大致思路是什么?
生:可类比平面向量基本定理,分存在性和惟一性来证明.
问题2
如何证明空间向量基本定理中的存在性?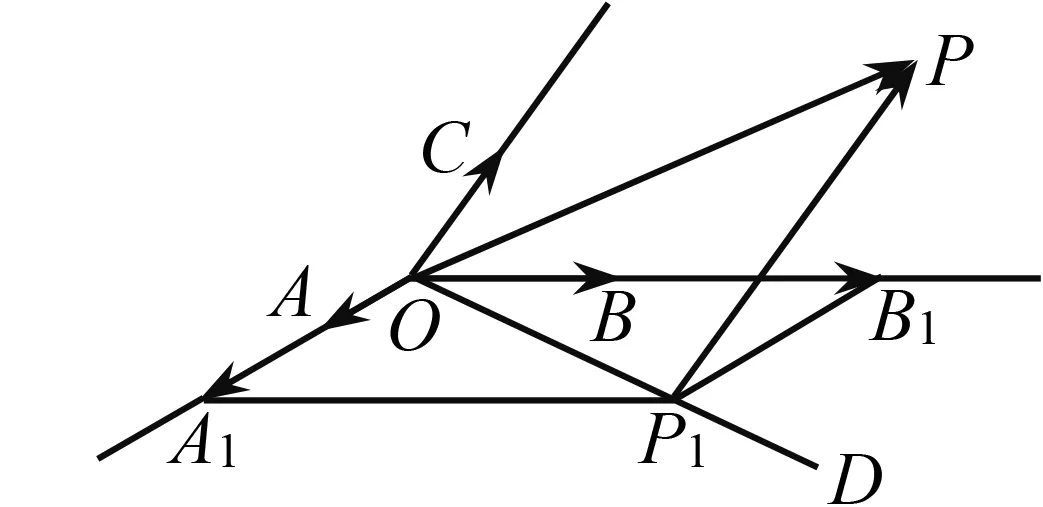
图1
师:如图1,设,,是三个共点且不共面的向量,其中对于空间任一向量,设=.如何将线性表示成的形式?生:过点P
作PP
∥OC
,交平面AOB
于点P
.师:这点P
具体在什么位置?生:点P
既在平面POC
内,又在平面AOB
内,故点P
在平面POC
和平面AOB
的交线上.师:很好.记上述交线为直线OD
,则点P
在直线OD
上(此时教师在图中作出直线OD
,PP
和OD
的交点就是P
),这样P
的位置就确定了,于是接下来怎么办?生:在平面AOB
内,作平行四边形OA
P
B
,满足A
,B
分别在直线OA
,OB
上,于是所以师:很好!接下来根据共线向量的条件,存在三个确定的实数x
,y
,z
,使得所以=x
+y
+z
.这就证明了存在性.追问 上述证明存在性用的是什么方法?
生:构造图形法.
提炼 证明存在性的问题,一般都用构造法.
问题3
如何证明空间向量基本定理中的惟一性?师:证明惟一性常用什么方法?
生:反证法.
师:下面用反证法试一试如何证明?
生:假设有两种不同的表示,分别为=x
+y
+z
,=x
+y
+z
,其中(x
,y
,z
)≠(x
,y
,z
),则有x
+y
+z
=x
+y
+z
,移项整理得(x
-x
)+(y
-y
)+(z
-z
)=0
.不妨设x
≠x
,则进而,,共面,这与已知条件,,不共面矛盾,因此只有惟一的一种表示,即有序数组(x
,y
,z
)是惟一的.师:说得非常棒!这就证明了惟一性.至此完成了对空间向量基本定理的完整证明.
练习 已知,,不共面,且x
+y
+z
=0
,则x
=y
=z
=.
提炼 空间向量基本定理告诉我们,空间中任意一个向量只需用三个不共面的向量就能线性表示,而且这种表示是惟一的.
追问1 空间向量基本定理中的三个不共面向量可以构成空间的一个,这三个向量叫作
.追问2 如果空间一个基底的三个基向量两两互相垂直,那么这个基底叫作
.追问3 如果空间一个基底的三个基向量两两互相垂直而且都是单位向量,那么这个基底叫作
,通常用
表示.
(在学生回答的基础上给出下面的概念)
基底、基向量、正交基底和单位正交基底 如果三个向量,,不共面,那么{,,}称为空间的一个基底,,,叫基向量.如果空间一个基底的三个基向量两两垂直,那么这个基底叫正交基底.特别地,当一个正交基底的三个基向量都是单位向量时,称这个基底为单位正交基底,通常用{,,}表示.追问4 如果把空间向量基本定理中的基向量{,,}改用任意一个向量改用会有一个什么样的结论呢?(在学生回答的基础上给出下列推论)
推论 设O
,A
,B
,C
是不共面的四点,则对空间任意一点P
,都存在惟一的有序实数组(x
,y
,z
),使问题4
如何运用空间向量基本定理解决问题?2
.
3 数学运用
例1
如图2,在正方体OADB
-CA
D
B
中,点E
是AB
和OD
的交点,M
是OD
与CE
的交点,试分别用向量表示和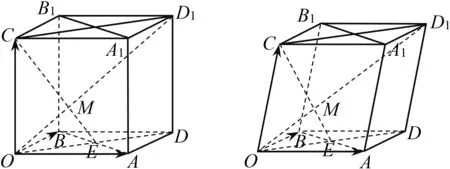
图2 图3
(学生口答,教师板书)
变式 该正方体为平行六面体(图3),其余条件不变,结果怎样?
生:结论也不变.
追问 上述图中点M
是△ABC
的心(从外、内、重、垂中选一个).
提炼1 上述正方体或平行六面体中的任意一个确定的向量都可以用惟一表示.
提炼2 在三棱锥O
-ABC
中,若点M
是底面△ABC
的重心,则例2
已知{,,}为空间一个基底,能否以作为空间的一个基底?分析 三个向量能否作为一个基底,关键看它们是否不共面.
解
假设共面.由于显然有与不共线,据共面向量定理可设于是+=x
(-)+y
(-)=x
+y
-(x
+y
).因为{,,}为空间一个基底,所以依据空间向量基本定理中惟一性,得此方程无解,矛盾!所以不共面,故能作为空间的一个基底.追问 能用上述基底表示向量吗?
生:能.
师:那又如何表示呢?
生:利用待定系数法,设即有4+-=(m
+n
)+(m
+k
)-(n
+k
).因为{,,}为空间一个基底,所以解之得因此,2
.
4 课堂小结
■本节课是如何研究空间向量基本定理的?(类比法猜想,构造法、反证法证明,运算法则法、待定系数法应用)
■空间向量基本定理、平面向量基本定理、共线向量定理有什么区别和联系?(略)
说明
前面标注■的问题称为“回问”.所谓“回问”就是反思提炼,总结提升.3 教学反思
本节课的教学设计没有采用新课程倡导的“问题情境—知识建构—知识运用—课堂小结”的模式,而是采用了原创的“四问驱动”的教学范式,主要基于以下两个原因:一是笔者目前主持的一项省规划办课题就是关于“四问驱动”范式的课题,所以采用“四问驱动”的教学范式进行授课可以丰富课题研究成果;二是倡导用“四问驱动”的范式培养学生发现问题、提出问题、分析问题和解决问题的能力,因为“四问驱动”范式就是为聚焦上述“四能”而设计的教学范式.
由于“四问驱动”教学范式有相对固定的模式,所以在教学设计时如何设计“四问”就显得非常重要.那么本节课是如何设计“四问”的呢?
第一、设计启问时要依据教学目标,并注意将启问前的问题情境设计得新颖简洁明了有趣.设计探问时要依据启问,并注意各探问之间呈并列或递进关系.设计追问时要依据探问,并注意让追问的思维量适当小一些,让思维的灵动在此能体现出来.设计回问时要把握课堂立意,把握深度学习,做到既有一般性的梳理归纳,又有画龙点睛式的拔高.而本节课在设计“四问”时,就是遵循上面的设计思路来进行的.在设计启问、追问和回问时都比较顺利,唯独在设计探问时出现了一个纠结,就是“基底概念和定理的推论”这个内容是作为探问给出来还是作为追问给出来,最终是把它们作为追问给出来.其原因是坚持探问之间的关系是并列或递进关系.
第二、根据“四问驱动”的含义,“四问驱动”中的问题应该具有驱动性,那么在进行“四问”设计时,如何体现驱动性?主要做法是:一方面让所有设计出来的问题都要有一定的思维量,而且问题之间要连贯并形成一个体系;另一方面,在授课时要留有时间让学生思考或演算,而不总是教师自问自答.
总之,运用“四问驱动”教学范式进行教学是一种新的尝试,其基本特征是:教学目标明确,教学内容结构化,课堂立意较高;制作课件时重视情境设计和四问设计,课堂实施时重视合作探究和“四能”培养等.本节课不足之处表现在学生动手依然偏少,变式训练还有待加强.

