基于区间粗糙数相似度的多准则群体决策方法及其应用
刘启函,叶国菊,刘尉*,赵大方
(1.河海大学理学院,江苏 南京 210098;2.湖北师范大学数学与统计学院,湖北 黄石 435002)
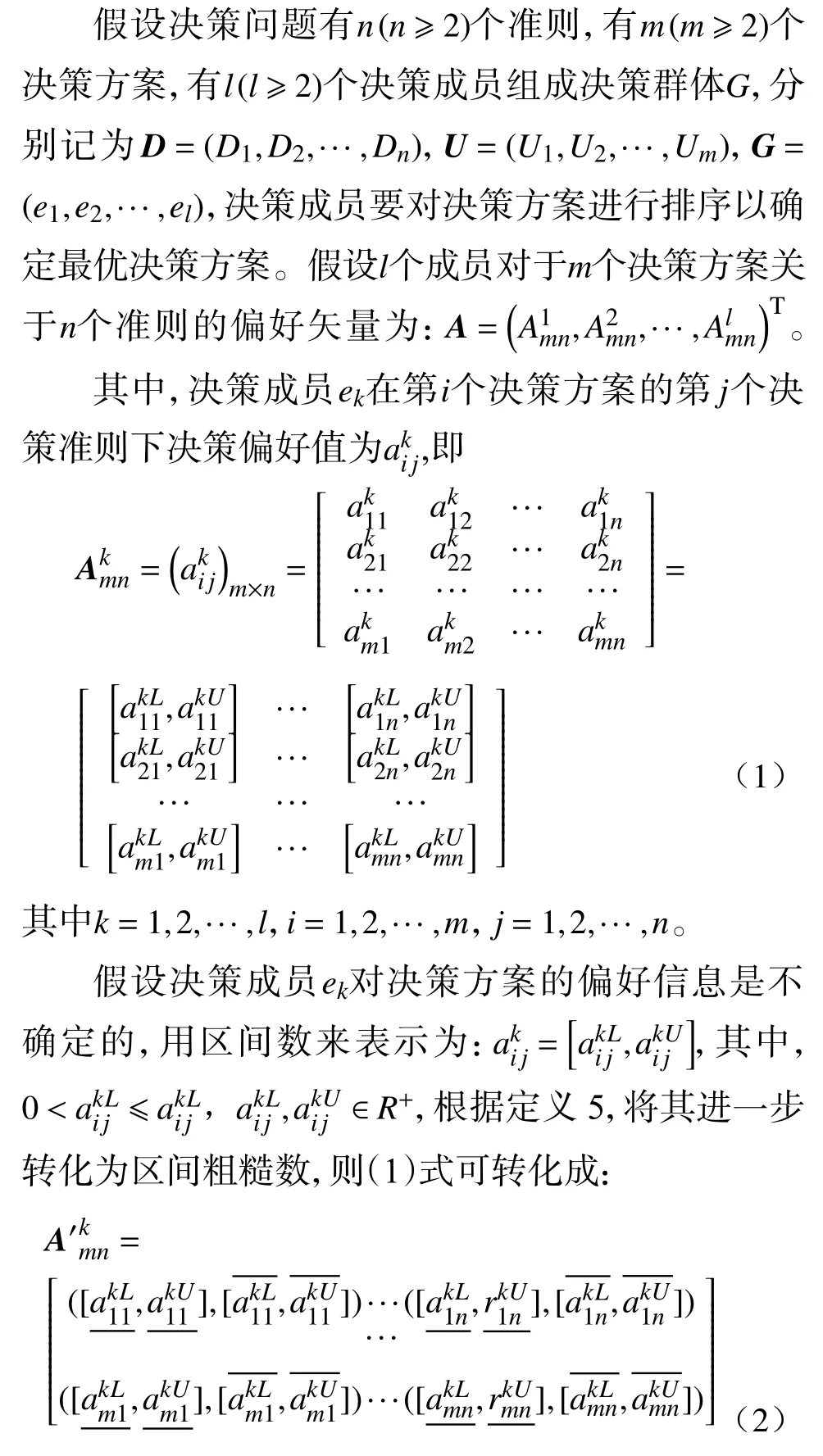
自1982 年PAWLAK[1]提出粗糙集后,粗糙集理论已在机器学习、数据分析与决策等众多领域得到应用。经典粗糙集只能处理属性为精确值的信息系统,但实际应用往往具有模糊性、不确定性等特点,用单一的数值形式并不能准确表达对象间的关系,导致经典粗糙集难以处理这些问题。因此,2002 年Liu[2]结合粗糙集与区间数,提出区间粗糙数的概念。区间粗糙数是利用上、下近似区间来描述数据的不确定性,比粗糙集更精准,更贴近实际,自2010 年,研究者已将区间粗糙数与TOPSIS、D-S 证据理论等多种方法和模型融合,在决策等领域中取得丰硕成果[3-8]。
多准则群体决策是决策科学中的热点研究领域,为在决策时避免因单个决策者的失误而导致决策错误,只有依赖各领域专家组成的多人决策进行群体决策,对此已有区间数[9]、区间直觉模糊数[10]等形式对其进行广泛研究。区间粗糙数作为处理不确定性问题的新型数学工具,针对区间粗糙数环境下的多准则群体决策值得深入研究。特别地,2011年王坚强等[11]引入区间粗糙算子,在确定决策准则的权重系数时应用区间粗糙数来处理模糊性;2016 年Zheng等[12]将区间粗糙数运用于开发混合质量功能展开(QFD)模型;2017 年Pamučar[13]基于区间粗糙数建立DEMATEL-ANP-MAIRCA混合模型解决群体多目标决策的新方法;2019 年Stević等[14]将区间粗糙数和简单加权法结合对供应商选择的多准则决策的问题进行处理,均得到较好的结果。但在现实情况中,方案间的相关性是实际决策需要考虑的关键之一,已有的研究中发现,大部分模型在求解准则权重时仅考虑了准则间的联系,忽视方案间的相关性。因此,本文利用面积比的思想提出一种新的区间粗糙数相似度公式,以描述方案间的联系,建立模型求解准则权重。本文中的相似度公式将上下近似区间的半径和中心点距离考虑在内,减少扰动,同时不需要专家的主观权重,计算更简便,结果更客观。
值得注意的是,在2019 年Cheng[15]等研究区间粗糙数信息系统时提到区间粗糙数相似度有较好的应用价值,然而目前仍处于理论阶段。因此,本文首次将区间粗糙数相似度运用到实际的决策问题中,对其进行应用扩充。此外,本文还对已有的区间粗糙数构造方法进行改进,使之满足定义条件,提高结果的准确性。最后,本文通过熵值法反映准则的客观联系,通过区间粗糙相似度反应各方案与标准方案之间的相关性,建立多目标优化模型求解权重,进而获得决策的排序结果,使排序结果更加贴近实际需求,为解决偏好值为区间数或区间粗糙数的多准则决策问题扩展了新方法。
1 理论基础
定义1[8](区间粗糙数)一个区间粗糙数是下近似和上近似均为区间的粗糙变量,记为:

其中c≤a≤b≤d,[a,b]为下近似区间,表示粗糙变量的极有可能取值范围,[c,d]为上近似区间,表示粗糙变量的确定取值范围。
定义2[8](区间粗糙数的基本运算)设ξi=([ai,bi],[ci,di])(i=1,2)为 两个区间粗糙数,k为实数,则有



在已有的文献中,构造的区间粗糙数并不满足定义1 中的c≤a≤b≤d这一条件,而本文中对区间粗糙数构造方法的改进,能够使之满足定义1 中的条件。
目前对区间粗糙数的相似度研究均是在区间相似度的基础上定义的,并且专家会对上下近似区间赋予一定的主观权重,这会使两个区间粗糙数之间的相似度带有主观影响。本文将区间粗糙数作为整体,采用面积比的思想,并考虑上、下近似区间的半径和中心点距离因素,以减少对相似度的干扰,由于避免专家对上、下近似区间的主观赋值,结果会更加客观。

2 基于相似度的区间粗糙数多准则群体决策模型
2.1 区间粗糙数多准则问题描述
基于上述决策群体的偏好矢量矩阵A′,综合准则的主客观联系,应用区间粗糙数获得相似度最大时对应的决策方案,也就是群体决策结果。
2.2 规范化处理
决策准则分为效益型和成本型两种,分别针对这两种类型的准则,对上述区间粗糙决策偏好矩阵(2)进行规范化[8]处理。
1) 对于收益型准则,转换公式为
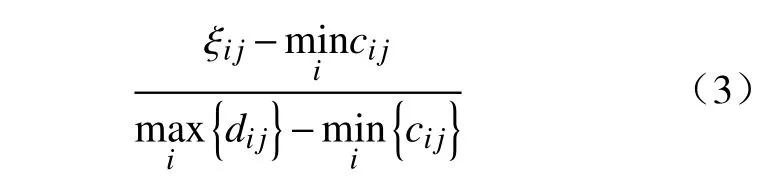
2) 对于成本型准则,转换公式为

将偏好矩阵归一化处理后,得到如下规范化偏好矩阵:

将第j列准则上m个方案的平均值作为每个成员的标准方案,即

2.3 决策准则权重的确定

决策准则权重的求解结合熵权法和相似最大化的方法。对于熵值法,若在多准则决策问题中,准则对决策方案的影响越大,那么其所占比重也越大,故建立如下极大熵模型:

而在整个决策方案中,方案间也存在相关联系。因此,建立各方案与标准方案的相似度最大化模型,以达到整体综合决策最接近标准方案的目标,模型如下:

上述为多目标规划模型,利用线性加权,将其转为单目标规划问题,如下:

由于 λ作为参数,可对它进行赋值,故在解该模型时,λ作为常数,构造拉格朗日函数

2.4 综合决策值

2.5 决策方案排序
根据定义3 及式(10),易知综合决策值中的元素均为区间粗糙数,根据定义4 的可能度计算公式,可以得到方案的可能度比较矩阵:P=(Ppq(Zp≥Zq))m×m,其中1 ≤p,q≤m。最后根据模糊互补判断矩阵[17]排序算法:

最后得到方案的排序向量为
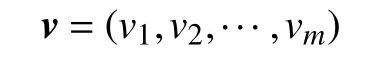
2.6 方法步骤
1)步骤1。根据定义5,将区间数的偏好矩阵转化成区间粗糙数偏好矩阵A’;
2)步骤2。根据公式(3)(4),将区间粗糙数矩阵规范化处理;接着根据公式(6),得到标准方案,并添加到区间粗糙偏好矩阵最后一行,得到扩展区间粗糙偏好矩阵;
3)步骤3。根据定义6,建立极大熵和决策方案相似度最大模型(9),求解决策准则的权重;
4)步骤4。分别赋予决策成员客观权重ω=(ω1,ω2,···,ωl),根据定义3,集结决策成员的权重和决策准则的权重,得到决策方案的综合权重值Z;
5)步骤5。根据定义4 的可能度计算公式,可计算得到可能度计算公式P;最后由公式(10)(11)得到各方案最终的排序向量v=(v1,v2,···,vm),值越大,方案越优。
3 实例分析
3.1 实例过程
采用文献[9]中的市场投资实例,来说明所提方法的有效性。
现投资公司拟进行一项投资,有4 个方案,记为U=(U1,U2,U3,U4),对应3 个投资准则,记为D=(D1,D2,D3),组织各个投资领域的 20名专家组成的决策群体,记为G=(e1,e2,···,e20)。用区间数来表示各专家的决策偏好值,设定初始评价的10 个评分等级为1 ~10。
1)步骤1。首先,为了使结果更贴近实际,根据定义5,将原始区间数转换成粗糙区间数,根据公式(3),将区间粗糙数矩阵规范化处理,规范化后数据如表1所示;
2)步骤2。根据公式(6),得到标准方案,并添加到区间粗糙偏好矩阵最后一行,得到扩展区间粗糙偏好矩阵,即表1中的第5 行;
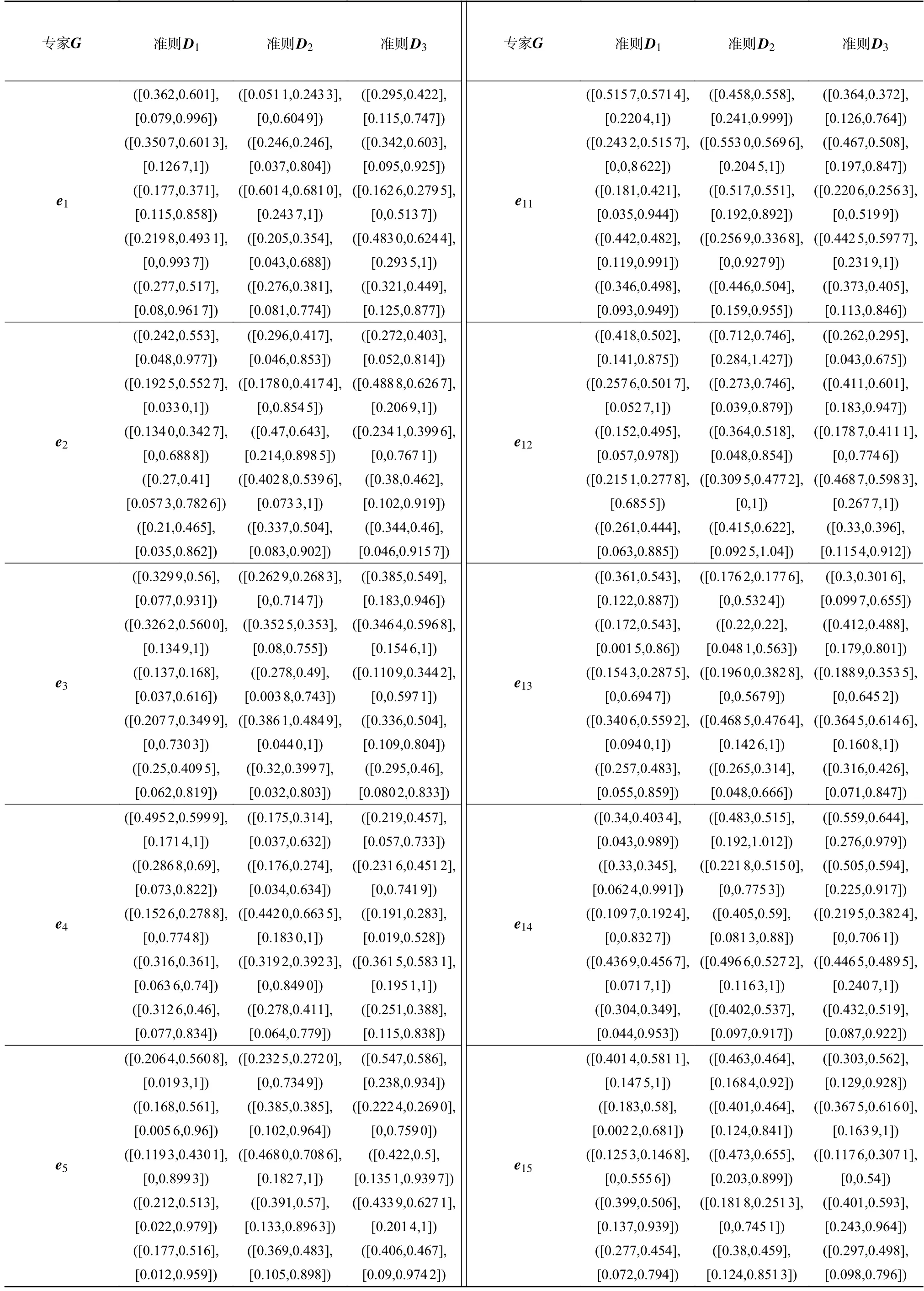
表1 规范化后的扩展偏好区间粗糙信息表

续表 1
3)步骤3。根据定义6,建立极大熵和决策准则相似度最大模型,根据目标规划,取λ=0.2,求解决策准则的权重,如下表2所示;
4)步骤4。分别赋予决策成员客观权重,此时,我们直接取文献[9]中决策成员的权重,如下表3所示;根据定义3,综合决策成员的权重和决策准则的权重,得到决策方案的综合权重值为:

表2 决策准则权重

表3 决策成员权重

5)步骤5。根据定义4 的可能度计算公式,取系数 λ1=λ2=λ3=λ4=,得可能度矩阵:

最后由公式(11)得到各方案的最终的排序向量

因此,投资优先顺序为U4>U1>U2>U3,则投资第4 个方案最佳。
注:本文的方法得到的排序结果与文献[9]得到的排序结果一致,因此,可证实本文的方法的有效性与合理性。
3.2 结果分析
在建立单目标规划模型(9)时,加入参数 λ,这时需要考虑 λ的不同赋值对结果有何影响。λ的取值由决策者主观偏好决定,当λ >0.5时,表明决策者更偏向决策方案与标准方案内部的相关性;当λ=0.5时,认为决策者对两者态度一致;当λ <0.5时,表明决策者偏向决策准则之间的客观联系。本文分别取 λ=0.2,λ=0.5,λ=0.8,进行比较分析,排序结果如表4所示。

表4 决策者不同态度的排序结果对比
分析上述结果:当 λ=0.2时,即决策者态度偏向准则之间的客观联系时,最优方案为U4,方案优劣与文献[9]一致,说明已有的排序方法均考虑准则之间的客观联系;当λ =0.5时,此时决策者赋予客观联系和内部相关性同等态度,U1为最优方案,此时方案优劣次序稍有变动;当λ =0.8时,即各方案之间的相关性被赋予较大权重时,可知最优方案为U1。观察不同态度下的结果可知,不管决策者的决策偏好是准则间的客观联系,还是方案间的相似性,方案U1和U4是可以优先考虑的策略。
由分析可知,对于准则权重的计算,将其内部关联性考虑在内时,根据决策者的态度不同,结果具有灵活性,因此,本文所提方法合理有效。
4 结论
在实际问题中,区间粗糙数更贴近现实情况,因此在已有研究的基础上,本文首先给出由区间数来定义区间粗糙数的方法。接着在区间粗糙信息系统下,针对准则权重未知的多准则群体决策问题,本文提出一种基于面积法的相似度的决策方法。该法以极大熵和相似最大化为目标,建立多目标优化模型,确定准则权重,然后,聚合决策成员权重,结合区间粗糙数的可能度,对方案进行综合排序。该法不仅能反映准则间的客观联系,而且也考虑了方案间的相关性,得到的结果更加贴合实际需求。此外,本文首次将区间粗糙数相似度理论用于实际决策中,丰富了区间粗糙数相似度的研究内容,并通过实例证明该方法是合理的、有效的。

