基于模糊β-覆盖的(I,T)-模糊粗糙近似算子
马欢,贺龙雨,候婷,秦克云
(西南交通大学数学学院,四川 成都 611756)
粗糙集理论(rough set theory,RST)是由波兰学者Pawlak[1]在1982 年创立的,是一种处理不确定性、不完整性信息的数学方法。该理论通过使用两个可定义的子集(称为上近似和下近似)来近似地描述不确定性概念。目前,这一理论已成功应用于数据分析与知识发现、模糊识别与分类、粒计算、不确定性决策等领域[2-5]。
在Pawlak 粗糙集模型中,对象之间的相似性通过等价关系表示,所有的等价类构成论域上的一个划分。然而,一些实际问题中所讨论的关系并不一定满足等价条件严格的标准。为此,学者们从实际应用背景出发,用一般二元关系[6-7]替换等价关系,将划分推广为邻域系统[8-9]和覆盖[10-11]等,提出了多种粗糙集的扩展模型。基于论域上的覆盖,Pomykala[12]得到了两对对偶的近似算子。Yao[9,13]通过邻域和知识粒,进一步研究了这些近似算子。该领域还有许多研究[14-16]被报道。
另外,经典的RST 在处理定量数据时也遇到了很大的限制。为了克服这一限制,Dubois等[17]将模糊集[18]与粗糙集结合,提出了模糊粗糙集和粗糙模糊集的扩展概念。后来,一些学者将覆盖粗糙集扩展到基于模糊覆盖的粗糙集。例如,通过使用模糊逻辑算子,Li等[19]提出了两对基于模糊覆盖的广义近似算子。此外,D’eer等[20-21]研究了基于模糊邻域系统、模糊极小描述和模糊极大描述的各种模糊邻域算子。然而,模糊覆盖的定义仍然具有一定的局限性。基于此,Ma[22]将模糊覆盖推广为模糊 β-覆盖,并通过模糊 β-邻域,提出了两种新的基于模糊覆盖的粗糙集模型。Yang等[23]进一步发展了模糊极小描述和模糊互补β-邻域,给出了另外3 种基于模糊覆盖的粗糙集模型。在此基础上,Zhang等[24]利用三角模和模糊蕴涵算子,对以上提出的基于模糊覆盖的模糊粗糙集模型进行了推广,并讨论了相关模型之间的关系。
值得注意的是,文献[22-24]提出的模型中的近似算子都是广义近似空间中基于对象生成的广义粗糙近似算子的推广形式。而在广义近似空间中,可以分别从对象、知识粒、以及子系统的角度构造不同类型的广义粗糙近似算子,它们具有不同的语义解释。本文从知识粒的角度对广义粗糙近似算子做进一步的研究,并结合模糊β-邻域和模糊逻辑算子,建立了两种新的基于模糊β-覆盖的广义模糊粗糙集模型,可以看作是连接覆盖粗糙集理论和模糊粗糙集理论的桥梁,对以后研究基于覆盖的模糊粗糙集在决策中的应用有一定的帮助。文中主要讨论了所提出的模糊粗糙近似算子的性质,并与现有的模糊粗糙近似算子进行比较分析,使得新的模糊粗糙近似算子和现有的模糊粗糙近似算子之间建立联系,为进一步讨论模糊粗糙近似算子的拓扑结构及其应用创造了条件。
1 预备知识
本节给出模糊逻辑算子、模糊集以及模糊β-覆盖近似空间中的相关概念与性质。
1.1 模糊逻辑算子


引理2设T是一个t-模,N 是一伪补。I是基于T和 N 的一个S-蕴涵算子,则引理1 中的3)、4)以及7)的第2 个等式仍成立。
注意:如果I是基于一个连续的t-模T和一个伪补 N 的一个S-蕴涵算子,则引理1 中的1)、2)、3)、4)、7)的第2 个等式、10)以及11)成立。
1.2 模糊集
设U是非空论域,称映射A:U→[0,1]为U上的模糊集。设F(U)是U的所有模糊集构成的集合,称其为U的模糊幂集[26]。
设A,B∈F(U)。如果对于任意x∈U,都有A(x)≤B(x),则称A包含于B,记A⊆B;A=B当且仅当A⊆B且B⊆A。A与B的并,A∪B∈F(U)且对于任意x∈U,有(A∪B)(x)=A(x)∨B(x);同样地,A与B的交,A∩B∈F(U)且 对于任意x∈U,(A∩B)(x)=A(x)∧B(x)。符号coN表示模糊补,即对于任意x∈U,(coNA)(x)=N(A(x))。
1.3 模糊β-覆盖近似空间

2 两种基于模糊β-覆盖的(I,T)-模糊粗糙集模型的建立
本节回顾广义近似空间中上下近似算子的定义,并给出两对基于模糊 β-覆盖的(I,T)-模糊粗糙近似算子。
定义5[29]设U是非空有限论域,R是U上的一个二元关系,即R⊆U×U,则称二元组(U,R)是一个广义近似空间。对于任意X⊆U,X关于近似空间(U,R)的两种形式的下近似与上近似分别定义为:

其中RS(x)={y∈U|(x,y)∈R},称为x关于R的右邻域。
已有文献通过模糊β-邻域、模糊互补β-邻域以及模糊逻辑算子,对式(3)和(4)进行了推广。如下定义:
定义6[24]设T和I分别是 [ 0,1]上的t-模和蕴涵算子,(U,C)是 模糊 β-覆盖近似空间。对于任意X∈F(U),X关于近似空间(U,C)的两种形式的下近似与上近似是如下定义的U上的模糊集,对于任意x∈U,


其中 XX为集合X的特征函数。将模糊 β-领域替换以上相应的二元关系,结合模糊逻辑算子,从对偶性角度出发即可得到定义7 中所提出的模糊粗糙近似算子。
3 基于模糊β-覆盖的(I,T)-模糊粗糙近似算子的性质
本节主要讨论两对基于模糊 β-覆盖的(I,T)-模糊粗糙近似算子的性质。
3.1 基于模糊 β-覆盖的(I,T)-模糊粗糙近似算子(,)的性质





3.2 基于模糊 β-覆盖的(I,T)-模糊粗糙近似算子(,)的性质


证明1)、2)、3)、5)和8)直接可证得。下面我们只给出4)、6)和7)的证明。
4)如果T是连续的,则对于任意x∈U,由引理1 的10)、11)及引理2 可得,
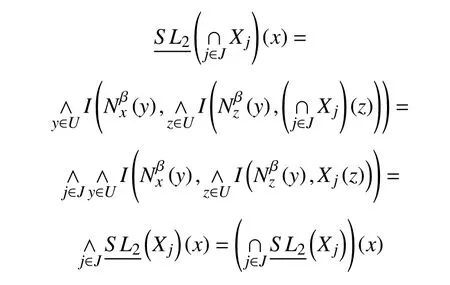



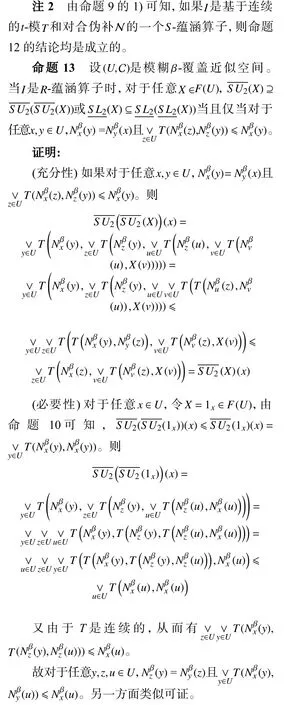
注3由命题9 的1)可知,如果I是基于连续的t-模T和对合伪补 N 的一个S-蕴涵算子,则命题13 也成立。
由命题12和命题13 可得如下推论。

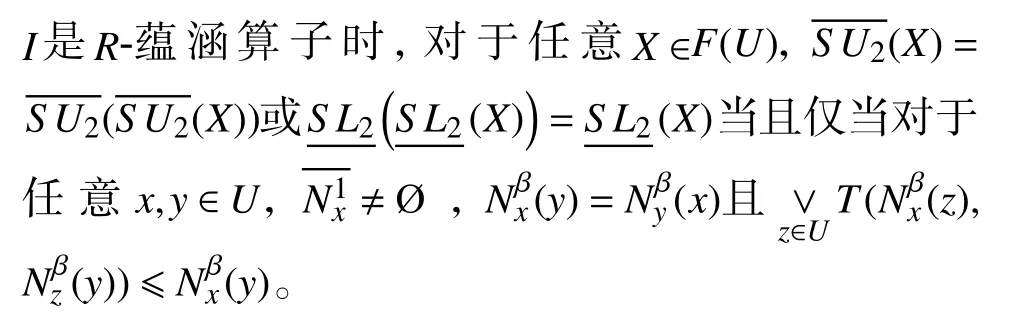
注4由命题9 的1)可知,如果I是基于连续的t-模T和对合伪补 N 的一个S-蕴涵算子,则推论3 也成立。
4 基于模糊β-覆盖的(I,T)-模糊粗糙近似算子的比较
本节主要讨论两对基于知识粒生成的(I,T)-模糊 β-覆盖粗糙近似算子与基于对象生成的(I,T)-模糊β-覆盖粗糙近似算子之间的关系,并给出相关近似算子等价的条件。


为讨论推论5 的必要性,给出下面的引理。
引理3设(U,C)是 模糊 β-覆盖近似空间。如果T是连续的,则对于任意x,y∈U,α∈[0,1],下列表述等价:

证明:( 1)⇔(2):对于任意x,y∈U,由1x的定义可知,1x(y)=0 ⇔y≠x。又由于T是连续的,则由引理1 的1)有
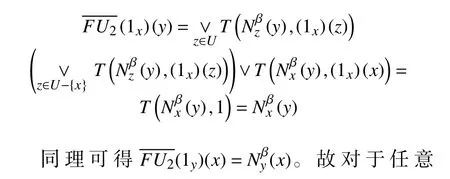

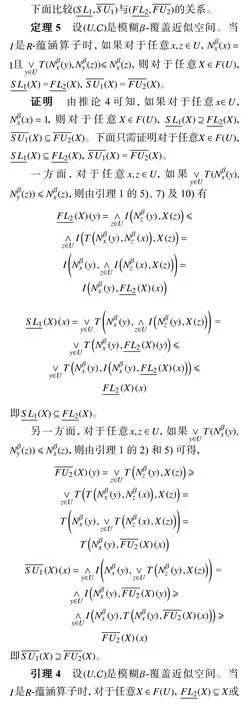

由以上结论,我们可得到下面的推论。

5 结论
本文通过模糊β-邻域以及模糊逻辑算子(三角模算子T和模糊蕴涵算子I),提出了两种基于模糊β-覆盖的(I,T)-模糊粗糙集模型,详细讨论了模糊粗糙近似算子的基本性质,刻画了基于对象与基于知识粒生成的(I,T)-模糊 β-覆盖粗糙近似算子之间的关系,并通过分析研究,给出了相关近似算子等价的充要条件。本文从知识粒的角度定义的两种基于模糊β-覆盖的广义模糊粗糙集模型,可以看作是连接覆盖粗糙集理论和模糊粗糙集理论的桥梁,对以后研究基于覆盖的模糊粗糙集在决策中的应用有一定的帮助。在后续的研究中,将进一步研究基于子系统生成的模糊粗糙近似算子,并尝试探索模糊拓扑与模糊β-覆盖之间的关系,进而研究近似算子的拓扑结构及其应用。

