基于组合赋权的数控机床精度模糊评价
封志明,闵兴龙,江维,赵帅
(西华大学机械工程学院,四川 成都 610039)
数控机床作为机械行业内制造零部件的母机,应用范围广、使用频率高,在精密级及超高精密级加工的应用更是难以替代。目前,市场上数控机床种类繁多,单一考察机床某一方面精度指标是不全面的,机床选择不当,会在生产成本、生产质量、生产率、市场份额以及环境等方面出现问题[1]。因此,有效评价机床精度是否适合当前加工目标是企业采购、选型时所面临的重要问题[2]。
数控机床整机精度主要包括机床静态精度、准静态精度和动态精度。在选择数控机床时,应对其整机精度进行多级考察与评价[3]。由Zadeh 提出的模糊集合概念[4]发展而来的模糊综合评价得到迅速发展,并在工程应用方面得到成功实践。要小鹏等[5]针对数控机床精度评价过程中定性指标不清晰、量化指标不准确等缺点,提出了一种基于区间可拓灰色模糊算法的机床精度评价方法;刘亮辉等[6]从机床的精度、加工性能、可靠性等5 方面建立数控机床性能指标评价体系,提出一种基于灰色关联度分析的数控机床性能模糊评价方法。以上方法为数控机床性能、精度模糊评价提供了参考,但是在确定评价指标权重时存在主观性偏强的问题。客观赋权依赖于样本数据,当样本数据变化时,权重也会发生变化,从而影响评价结果的可靠性[7]。为减少信息的损失,使赋权结果与实际结果尽可能接近,近年来,主客观组合赋权法在模糊综合评价中得到广泛的应用。李波等[8]利用可拓层次分析法和熵权法分别对评价指标进行了主、客观权重组合赋权,完成了数控机床的绿色性评价。刘鹏程等[9]基于组合赋权法对制造业服务商的业务协同能力进行了评价。本文提出一种基于序关系分析法的主观权重和熵值法的客观权重组合赋权法,并利用模糊综合评价法对数控机床的精度进行评价。
1 模糊综合评价模型
1.1 模糊综合评价理论
事物受多种因素以及自身属性影响,评价时需对事物各方面进行综合分析。事物内外因素和自身属性存在无法定量的问题,即具有模糊性,对模糊因素做出综合评判即为模糊综合评价[10]。
综合评价(comprehensive evaluation,CE)须对被评价对象进行合理、客观以及公正的综合评价。通过将评价指标、评价等级、权重系数以及集结模型结合,各个部分组合,推演出主观权重和客观权重,再进行多级融合,形成新的集成因素综合评价。
1.2 评价信息
评价指标将复杂评价目标分解为指标的集合,以供分级逐步评价。在实际应用中,应选取适合的评价指标进行分解,指标过多或过少在一定程度上会导致评价结果偏差过大。
评价等级是利用评价人员对于评价指标给出的等级集合,利用自然语言{很好,较好,一般,较差}作为评价指标的4 个等级,采用隶属度函数度量不同的评价等级。
1.3 模糊评价体系的建立
模糊评价是基于影响多因素、事物多属性的问题构建多层级评价体系模型[11]。将各类影响因素细分为若干层,对每层级进行初级综合评价,通过递推方式得到高层级综合评价,最终得到评价结果。图1所示为n阶二级评价模型示意图。
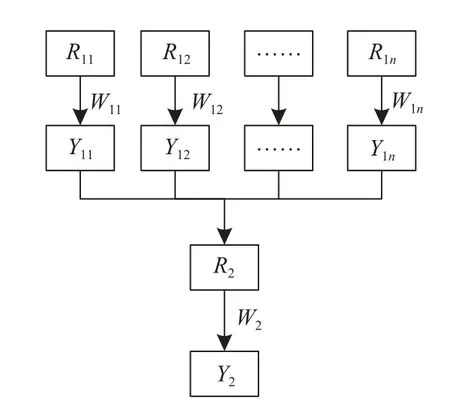
图1 二级评价模型示意图
图中R1i为单因素矩阵,W1i为对应权重矢量,故有一级评价矢量为
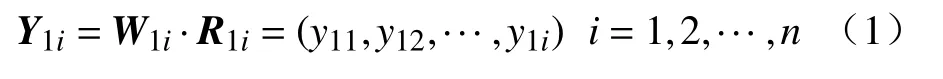
Y1i可组合成高层级评价矩阵,通过模糊计算,获得二级综合评价矢量,为Y2=W2·R2=(y21,y22,···,y2n)。
同理,在此基础上,可推导至更高层级评价。
2 主客观组合赋权法
在模糊综合评价中,权重的确定很重要,对最终结果起着决定性的影响。针对主观权重法人为因素太强、客观权重法过于依赖样本的问题,本文采用组合赋权方法作为权重系数的计算方法:主观权重系数利用序关系分析法[12],该方法是基于层次分析法的改进,无需构建判断矩阵,除去一致性检验计算外,综合计算量较少;客观权重系数采用熵值法[13]作为量化方法;将主、客观权重进行乘法合成归一组合得到主客观复合权重系数[14]。
2.1 基于序关系分析法的主观权重
序关系分析法通过采纳专家意见对指标集进行重要性赋值排序,根据赋值参考表确定指标相互之间重要程度,最后计算得到权重系数。
假设评价指标xi的重要性不低于xj,记为xi>xj。对于指标x1,x2,···,xn,对其进行处理有x2>x1>···>xn,处理后相邻量指标的重要性之比为:bi=wi-1/wi(i=n,n-1,···,2),wi为xi的权重,bi的赋值如表1所示。

表1 bi 赋值参考表
主观指标权重系数计算公式为:
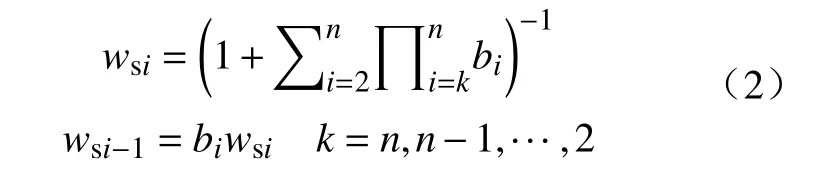
2.2 基于熵值法的客观权重
熵值法中,假设有m个评价指标,n个评价对象,组合成原始矩阵,对于指标i,指标值差异越大,在综合评价中的作用就越大。若指标的值全部相等,则该指标在综合评价中作用不大。
确定熵值法中的权重是将原始矩阵设为m个评价指标,n个评价对象,即为
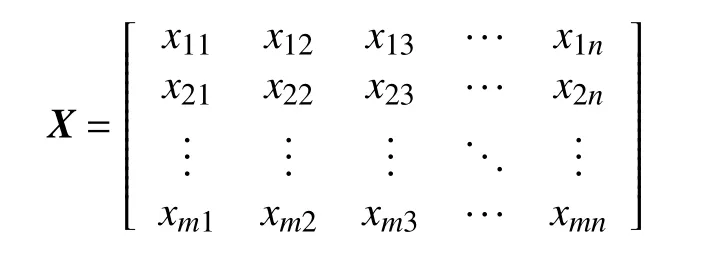
对X矩阵标准化处理,即选大者为优或者选小者为优,得到判断矩阵为第j评价对象对于第i评价指标上的标准值,且rij∈[0,1]。对于大者为优的效益型指标有

定义熵在m个评价指标,n个评价对象的问题中,第i个指标的熵hi为

2.3 主、客观权重权值复合
将主、客观权重进行归一化组合,得到最终权重系数,其计算公式为
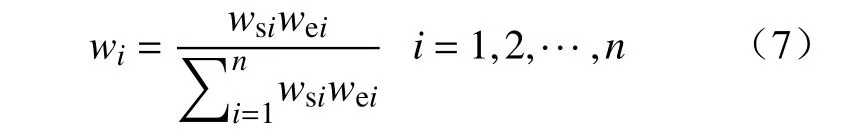
3 数控机床精度评价实例
3.1 机床精度评价体系的构建
采用HSD1615 数控龙门加工中心作为实验对象,该机床简化模型如图2所示。
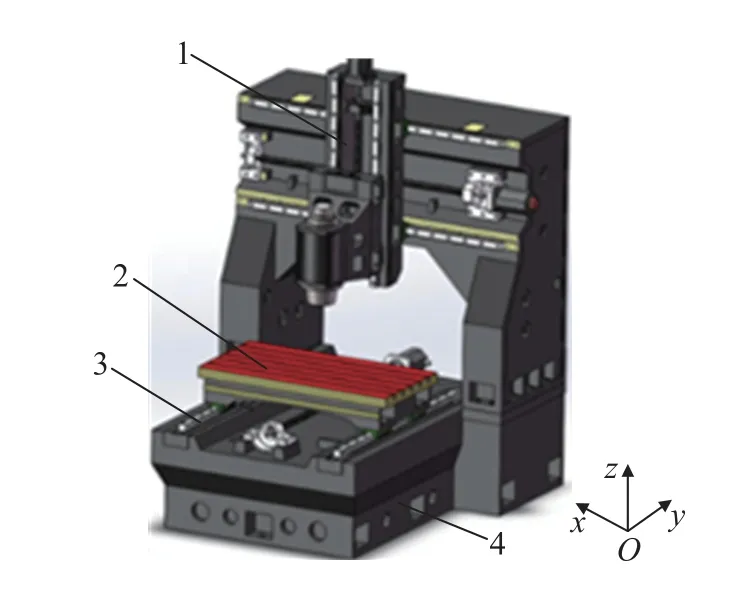
图2 数控龙门铣床简化模型
影响机床精度的因素众多,因此精度评价体系的建立至关重要。为了降低评价的风险,精度评价指标的选取应遵循以下原则[5]:1)评价指标项的选取应尽量全面;2)选取的评价指标项应较容易获取数据;3)选取时应尽量能参考机床精度检测标准;4)选取时应多方咨询行业企业专家意见。
根据以上原则,利用层次分析法思想,根据企业实际情况,针对该龙门铣床建立了如图3所示的精度评价指标体系。该体系包含3 个层次,第1 层为总目标即数控机床整体精度因素集U={U1,U2};第2 层为第2 级目标因素集Ui(i=1,2),其中,U1为静态误差因素集,U2为动态误差因素集,U1={J11,J12,J13,J14,J15,J16},U2={U21,U22,U23};第3 层为第3 级目标因素集U2i(i=1,2,3),其中,U21={D11,D12,D13,D14,D15,D16},U22={D21,D22,D23,D24,D25,D26},U23={D31,D32,D33,D34,D35,D36}。
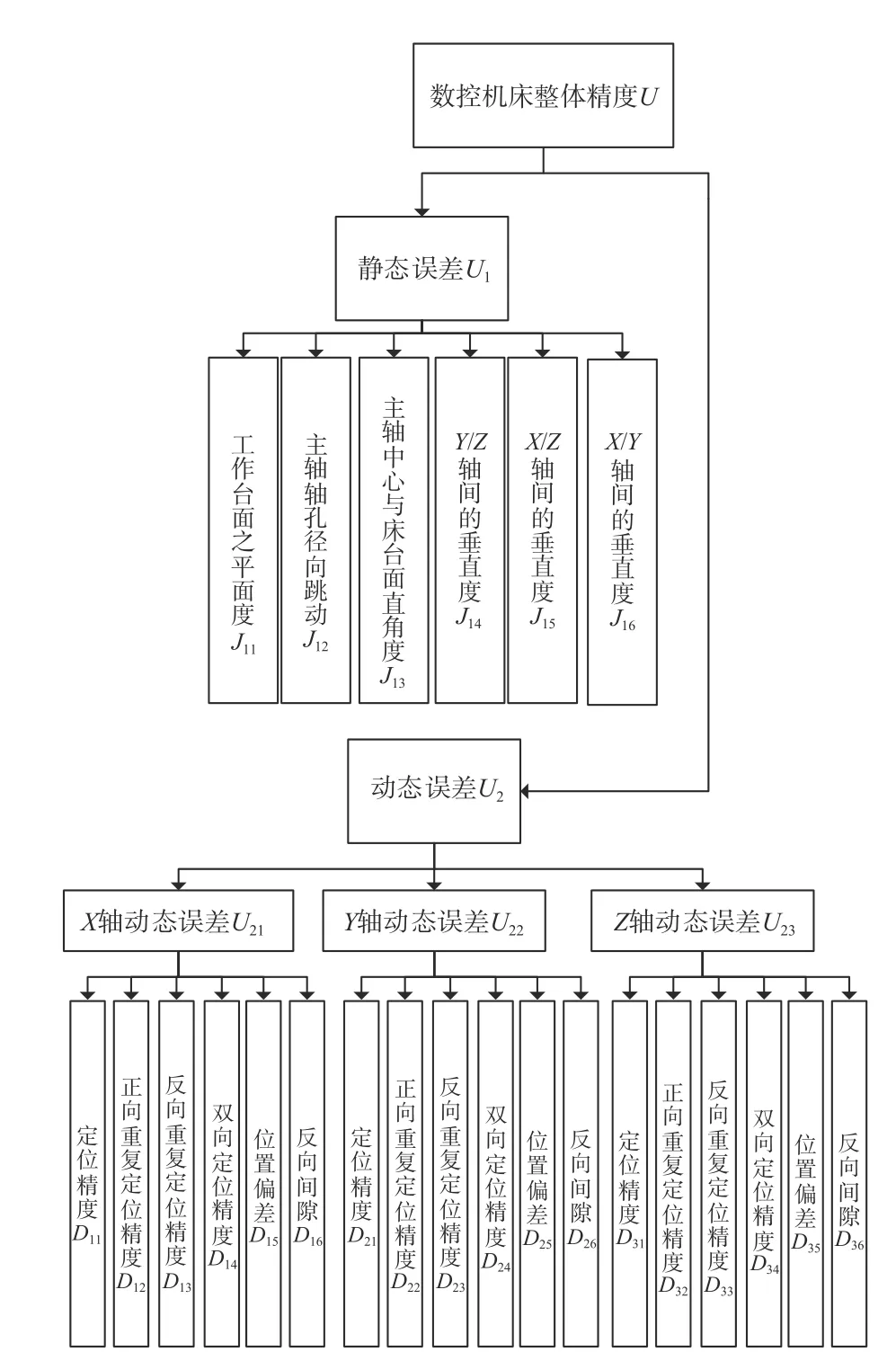
图3 数控龙门铣床精度评价指标体系
3.2 机床误差测量
机床误差测量严格遵守JJF 1251—2010《坐标定位测量系统校准规范》[15],根据图3所示的机床精度指标进行检测。机床X轴、Y轴、Z轴的定位精度,正向重复定位精度,反向重复定位精度,双向定位精度,反向间隙及位置偏差等动态误差试验数据,如表2所示。机床Z轴运动和Y轴运动间的垂直度、Z轴运动和X轴运动间的垂直度、X轴运动和Y轴运动间的垂直度、工作床台面平面度、主轴中心与床台面直角度及主轴轴孔径向跳动等静态试验数据如表3所示。
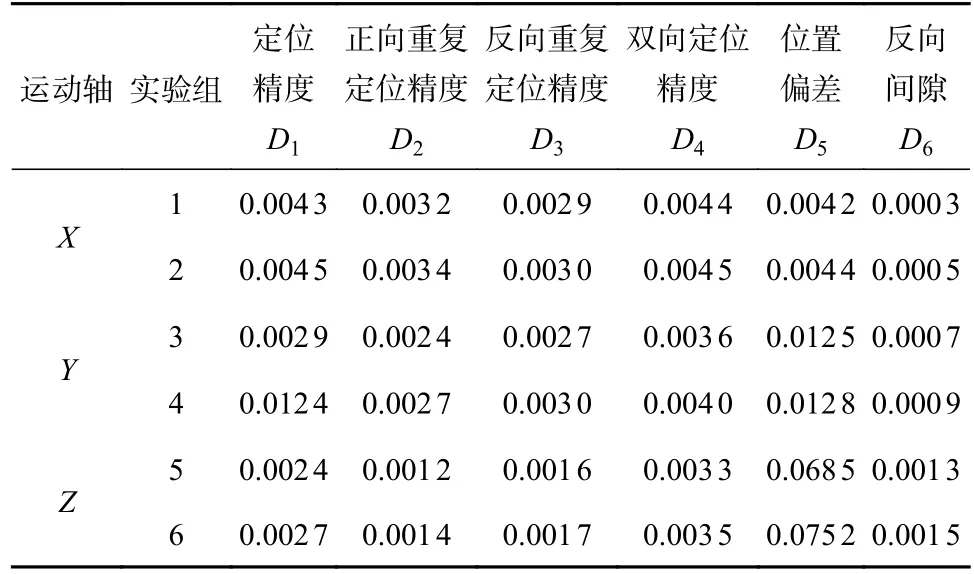
表2 动态误差试验数据 mm
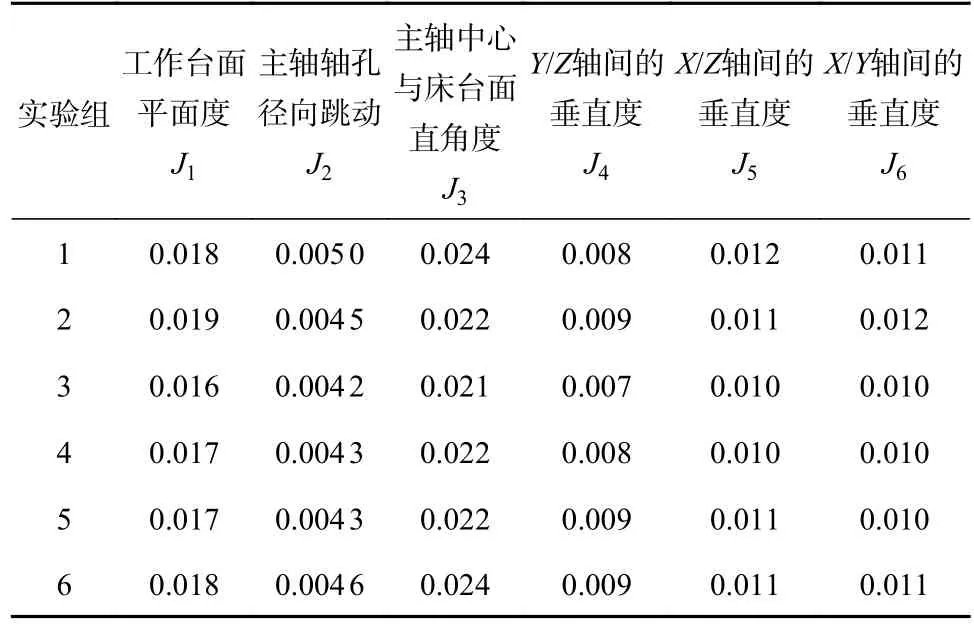
表3 静态误差试验数据 mm
为直观清晰地反映试验数据的容错性,绘制了关于机床X轴、Y轴、Z轴三轴的动态误差试验数据折线图,如图4—9所示。由图可知,动态误差在第2 组数据时出现突变,但定位精度无明显影响。图4中第8 组数据Y轴定位精度有明显突变,但对正反向重复定位精度、双向定位精度、位置偏差及反向间隙无明显影响。分析原因可能是测试工具出现误差或与动态误差指标间的联动性有关。
3.3 动态误差主客观组合赋权
3.3.1 动态误差指标主观权重确定
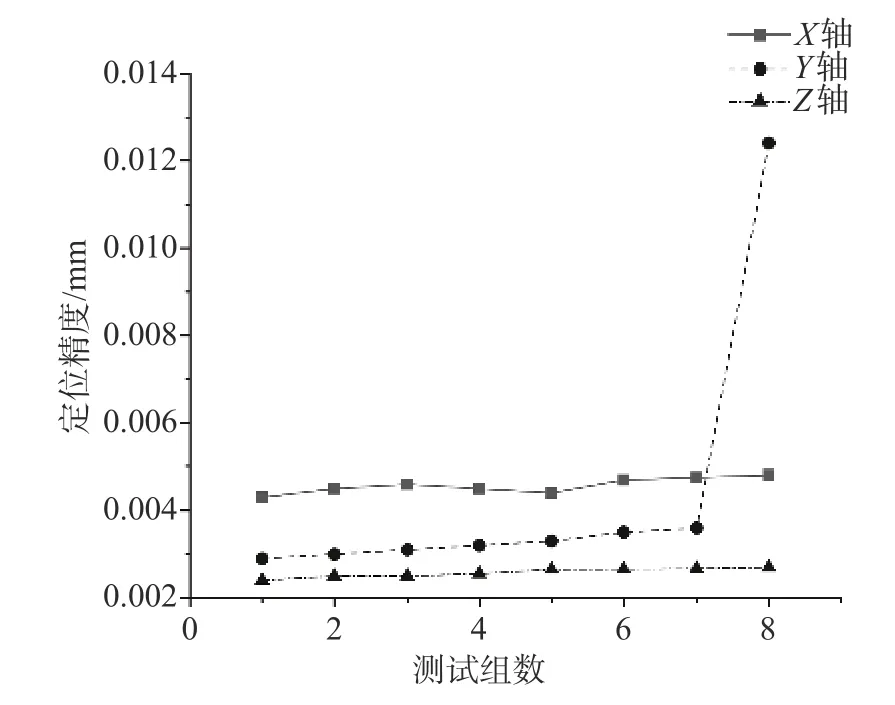
图4 X/Y/Z 定位精度
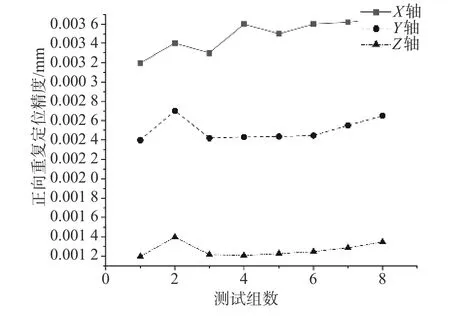
图5 X/Y/Z 正向重复定位精度
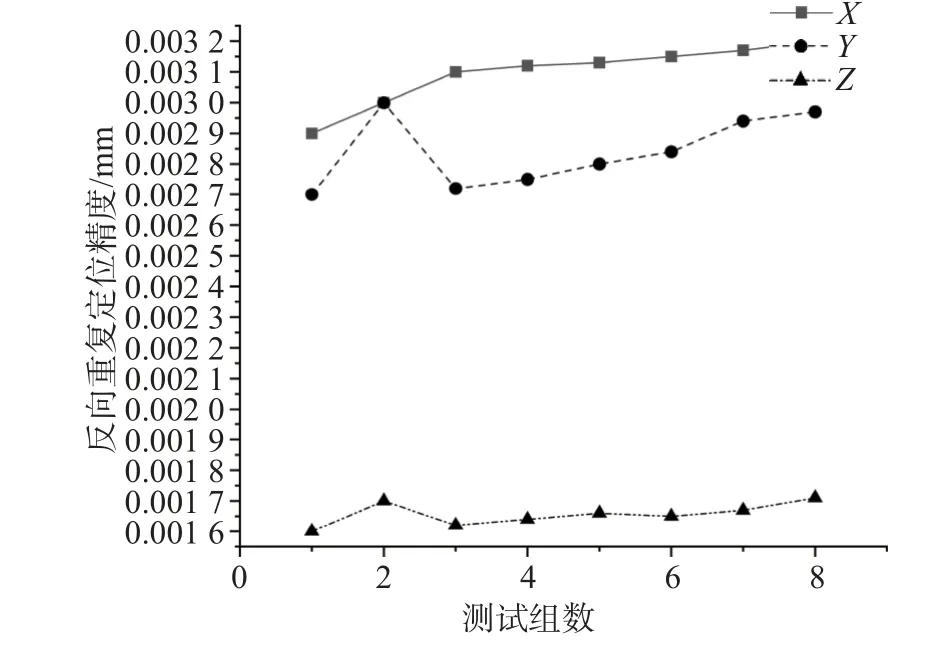
图6 X/Y/Z 反向重复定位精度
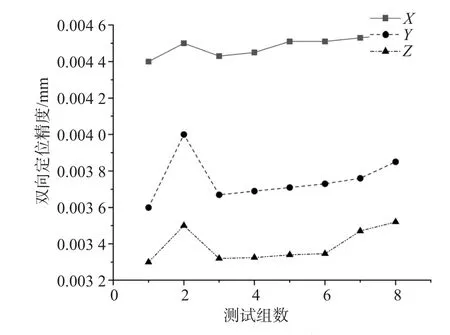
图7 X/Y/Z 双向定位精度
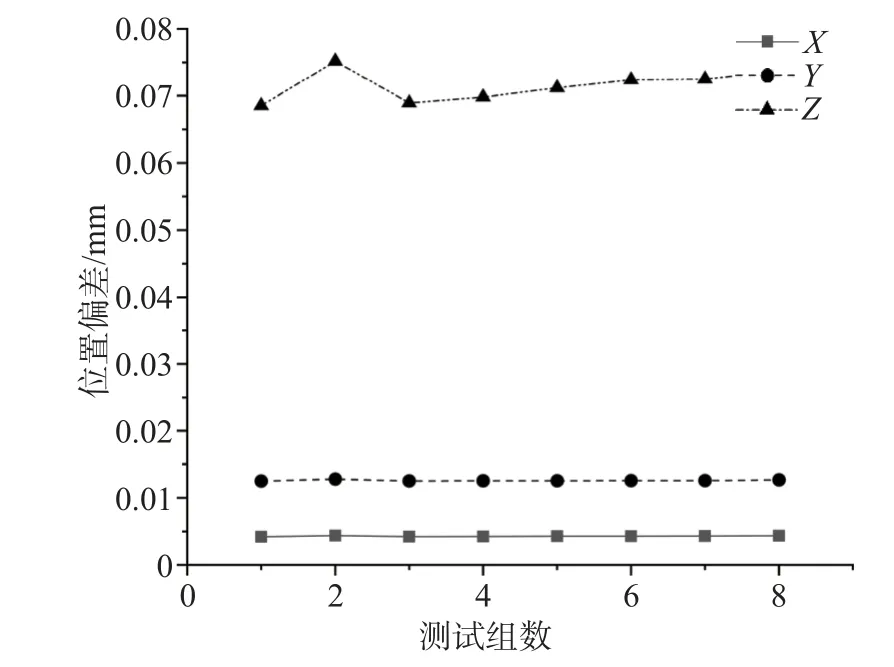
图8 X/Y/Z 位置偏差
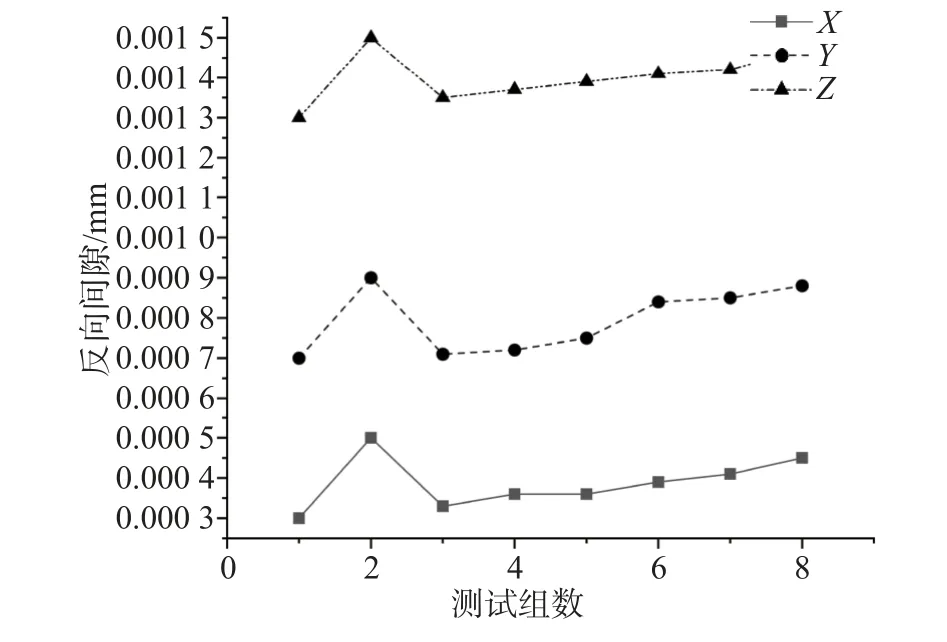
图9 X/Y/Z 反向间隙
为确定主观权重矩阵,成立50 位企业专家组成的评审组,通过问卷调查法,收集关于动态误差指标重要性的意见,对指标集U2={定位精度D1,正向重复定位精度D2,反向重复定位精度D3,双向定位精度D4,位置偏差D5,反向间隙D6}进行重要性排序,得到重要性关系排序为D1=D2=D3=D4>D5>D6。设{bi}为赋值矩阵,根据重要性赋值表1和专家组调查结果,得到Bi=[1,1,1,1.4,1.2],再根据式(2) 计算HSD1615龙门加工中心动态误差主观权重,得到主观权重向量Ws,为
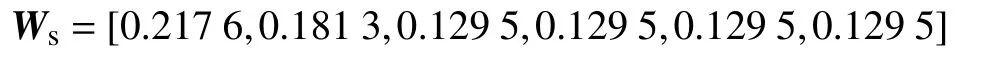
由此,X、Y、Z轴动态误差主观权重如表4所示。
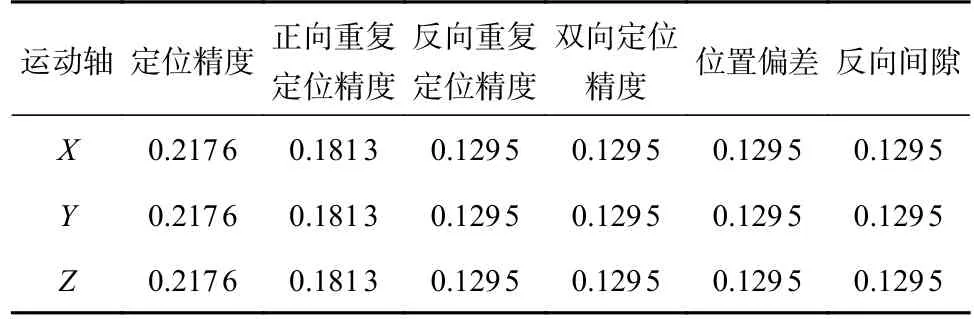
表4 X、Y、Z 轴动态误差主观权重分配表
3.3.2 动态误差指标客观权重确定
通过试验数据构建各轴动态误差矩阵,并以此建立原始数据矩阵对于指标i,误差值xij,选用小者为优的成本型指标,即根据式(4)建立判断矩阵R。
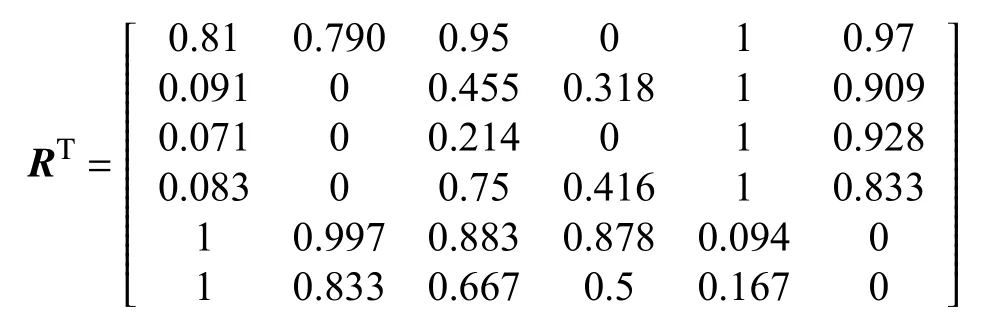
根据机床动态误差测试试验,得到原始数据矩阵X,为

对于小者为优指标而言,通过式(4)计算得到判断矩阵,为
根据式(5)中fij计算方法,可得
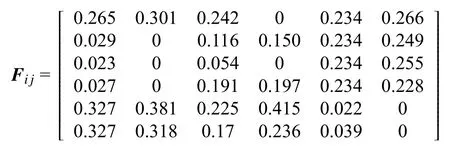
通过将判断矩阵转置后,利用式(5),计算得到所有动态指标的熵,为Hi=(0.976 0.741 0.522 0.788 0.847 0.836)。
通过式(6),计算得到所有指标的熵定义权重矩阵,为We=[0.018 3,0.201 6,0.370 7,0.164 2,0.118 5,0.126 8]。
3.3.3 主、客观组合赋权
通过组合赋权将主、客观权重合成。本文使用归一化式(7)的方式进行合成,即
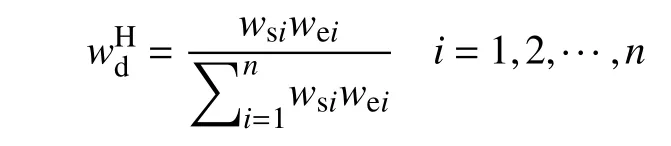
3.4 动态误差单因素评价矩阵
为了提高动态误差评价结果的客观性,成立50 位企业专家组成的评审组,通过问卷调查,由评审组专家对动态误差各因素评价,得到评判统计表,如表5所示。
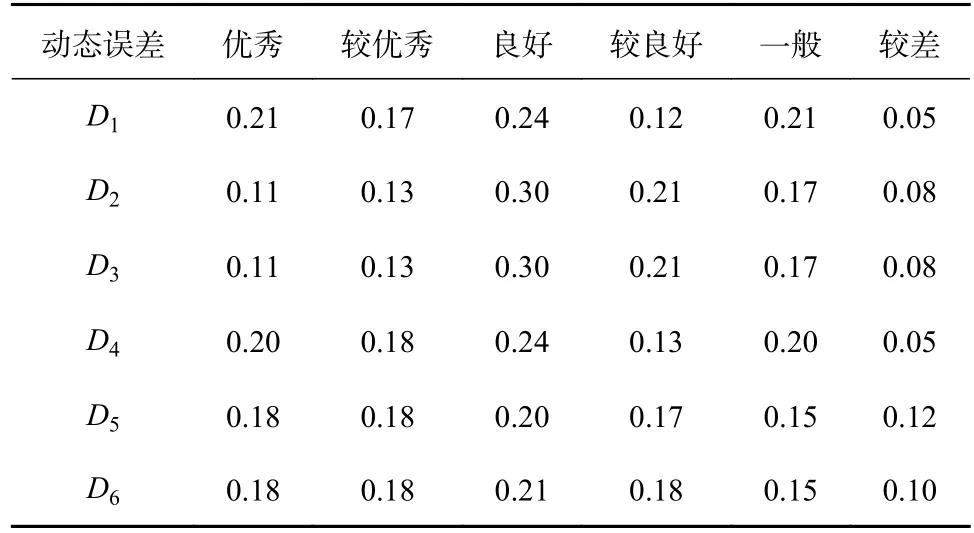
表5 动态误差单因素评判统计表
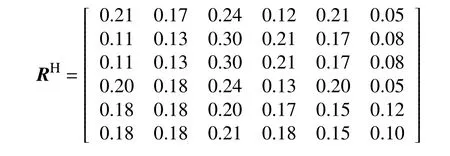
将表5内动态误差评价数据组合为单因素评价矩阵RH,即
对单因素评价矩阵,通过综合评价模型推导,利用式(1)得到动态误差评价矢量Y1,为
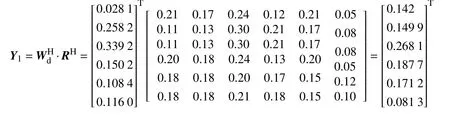
式中:为动态误差组合权重;RH为对应因素评判组成的评价矩阵。
3.5 静态误差主、客观组合赋权
3.5.1 静态误差指标主观权重确定
为确定主观权重矩阵,成立50 位企业专家组成的评审组,通过问卷调查,收集关于静态误差指标重要性的意见,将静态误差指标集U1={工作台面平面度J1,主轴轴孔径向跳动J2,主轴中心与床台面直角度J3,Y/Z轴间的垂直度J4,X/Z轴间的垂直度J5,X/Y轴间的垂直度J6}进行重要性关系排序,得到重要性关系排序为J1=J2=J3>J4=J5=J6。设{bi}为赋值矩阵,根据重要性赋值表1,得到赋值矩阵Bi=[1,1,1.4,1,1],再根据式(2)计算静态误差主观权重,得到各静态误差主观权重矢量,为Ws=(0.225 8,0.225 8,0.225 8,0.161 3,0.161 3,0.161 3)。
3.5.2 静态误差指标客观权重确定
通过试验数据构建各轴静态误差矩阵,并以此建立原始数据矩阵对于指标i,误差值xij,选用小者为优的成本性指标即式(4)建立判断矩阵R。根据机床静态误差测试试验,得到静态误差原始数据矩阵X,为
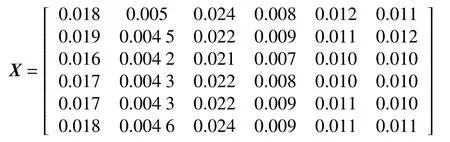
对于小者为优的成本型指标而言,通过式(4)计算得到判断矩阵,为

根据式(5)中fij的计算公式,可得
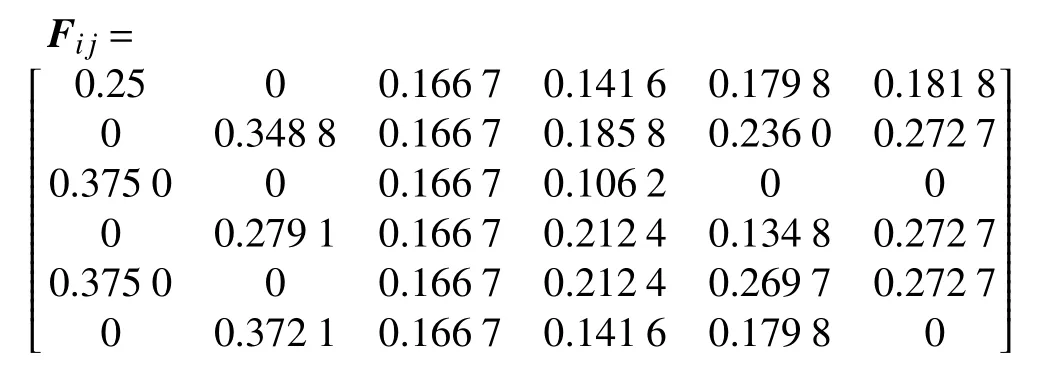
通过将判断矩阵转置后,利用式(5)计算得到所有静态指标的熵,为Hi=(0.859 8,0.934 2,0.504 9,0.897 7,0.950 6,0.698 7),随后通过式(6)计算得到所有指标的熵定义权重矩阵,为We=[0.121 5,0.057 0,0.429 0,0.088 7,0.042 8,0.261 1]。
3.5.3 主、客观组合赋权
通过组合赋权将主、客观权重合成。本文使用归一化式(7)的方式进行合成,即
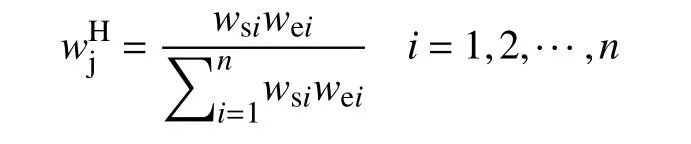
3.6 静态误差单因素评价矩阵
为了提高静态误差评价结果的客观性,成立50 位企业专家组成的评审组,通过问卷调查,由评审组专家对静态误差各因素评价,得到如表6所示的评判统计表。
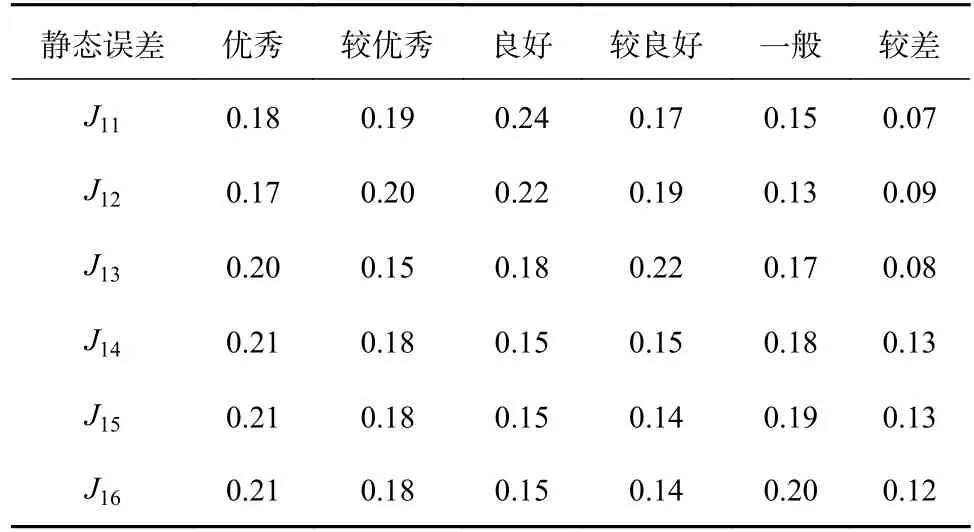
表6 静态误差单因素评判统计表
故有单因素评价矩阵为
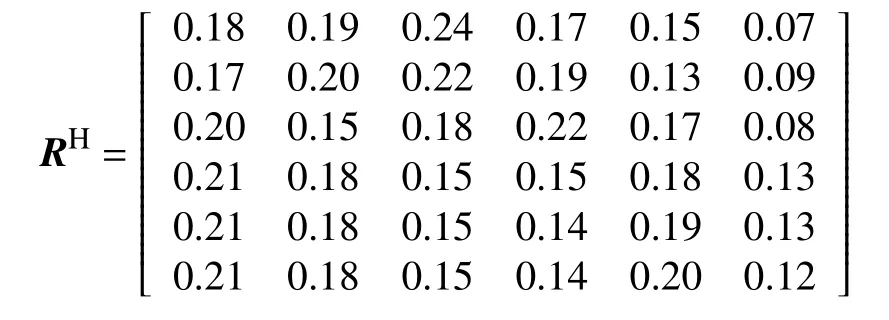
对于静态误差单因素评价矩阵RH,通过综合评价模型推导,利用式(1)得到评价矢量,为
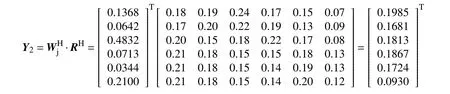
式中:为静态误差组合权重;RH为对应因素等级评价组成的评价矩阵。
3.7 数控机床精度综合评价
通过层次分析法,将最终决策定量与定性参数合理统一于模型[16]中,采用9 标度[17]建立判断矩阵A,为
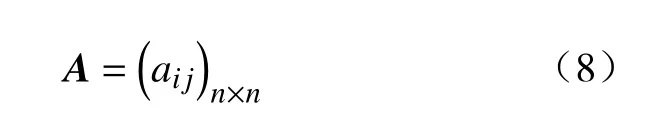
式中:A表示目标;i和j表示评判因素。具体定义如表7所示。
由文献[17]可知,平均随机一致性指标RI=0,然后计算一致性指标(consistency index,CI)和一致性比例(consistency ratio,CR),得到CI=0,CR=0,故判断矩阵符合逻辑,通过一致性检验。评价权重过程如表8所示。

表7 标度定义

表8 评价过程
当n=2 时,平均随机一致性指标RI=0,即CR=0、CI=0;判断矩阵A中动态指标和静态指标同样重要:因此,其权重为Wi=(0.5,0.5)。
将动静态指标评价矢量Y1、Y2组合,得到综合评价矢量RHSD,为

将综合评价矢量RHSD与指标权重Wi合成,即通过式(1)计算得到YHSD,为
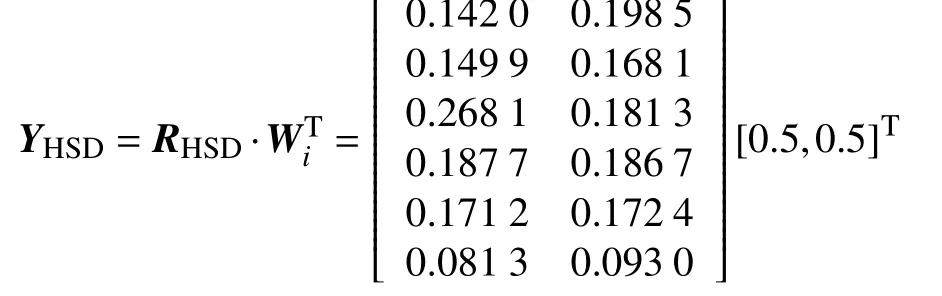
故主、客观复合的模糊评价结果YHSD=[0.170 3,0.159 0,0.224 7,0.187 2,0.171 8,0.087 1]T。
主、客观复合权重的模糊评价结果采纳最大隶属度原则。若评判结果向量Y中出现至少2 个相等的最大分量,即i≠j时,有yi=yj=maxyn,则模糊评价结果无作用[18];反之评价结果合理。分析各矢量,均没出现相同最大值,故评价结果Y有效。
使用MatlabR2019 的模糊逻辑工具箱,构建了数控机床精度综合评价模糊推理系统,如图10所示。
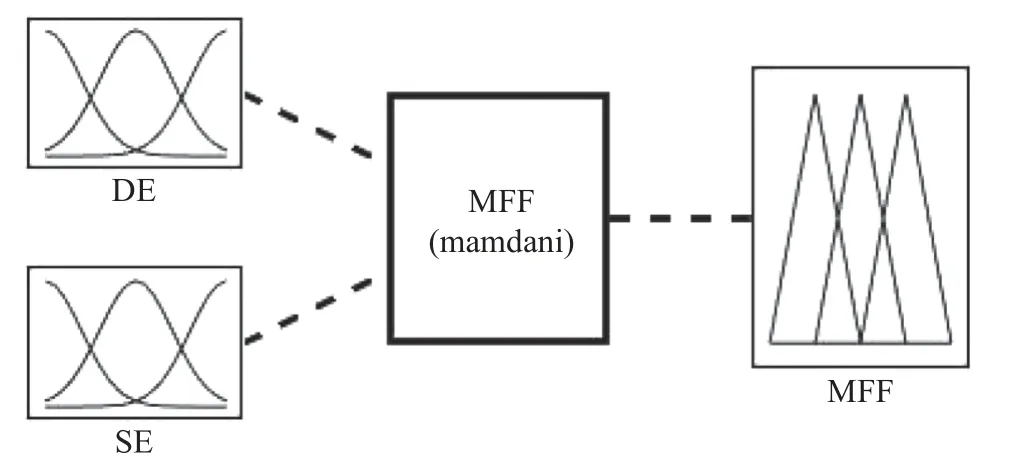
图10 数控机床精度综合评价双输入模糊推理系统
该系统具有2 个输入(静态误差U1,动态误差U2)。该模糊推理系统的输入和输出均使用三角隶属度函数,所有隶属函数的范围均为[0,1]。
由综合评价矢量可知,HSD1615 龙门加工中心精度评价为良好,其隶属度为0.224 7。
笔者从原始数据、评判过程及出厂检验报告中得到不同指标的数值范围,并通过调整敏感指标数值进行了多次实验。实验结果发现,“主轴轴孔径向跳动J2”“X/Z轴间的垂直度J5”指标数值偏离均值较远,说明在机床装配工艺或使用过程中出现一定问题,为此,可从这类问题溯源,提高数控机床的整机精度。本文在对数控机床评估过程中,采用主、客观组合,动、静误差综合的方式,增加了评价元素,从而提高了机床整体评价的客观性。
4 结论
本文以数控龙门铣床为例,面向数控机床精度评价的实际需求,分析了当前主客观权重模型中存在的问题,提出了基于主、客观组合赋权的数控机床精度模糊综合评价模型。通过序关系分析法和熵值法分别确定主观权重及客观权重,采用乘法合成归一将主、客观权重复合,并进一步结合层次分析法构建目标权重矢量,然后通过建立数控机床评价指标的判断矩阵,利用模糊综合评价法完成机床的整体精度综合评价。多次实验结果表明,该方法是合理的、可行的。实验还发现“主轴轴孔径向跳动”“X/Z轴间的垂直度”评价结果偏低,说明机床装配工艺或使用过程中会出现一定问题,因此,可从这类问题溯源,以提高数控机床的整机精度。该方法对于其他多因素、多属性复杂机电产品的综合评判具有一定参考作用。

