出入相补原理的内涵及其在小学数学教学中的价值

黄仙凤，黄红倩，李织兰

（1.百色市田阳区第二小学，广西百色 533600；2.桂林学院理工学院，广西桂林 541006；3.桂林师范高等专科学校教务处，广西桂林 541199）

出入相补原理是中国古代几何学中最基本的一条原理，出现在小学五年级数学教材（人教版）的“多边形面积”单元的“你知道吗？”栏目，它的价值主要在于对小学生的观念及思维方式的影响，具有科学和人文的教育价值。一方面，学生在数学学习中体会数学的应用价值，激发学生的创新思维，提高运用数学知识和方法解决问题的能力；另一方面，对学生良好品德的养成、思维能力的提升、理性精神的培养和陶冶具有独特的意义。

目前，部分教师在数学教学中还存在这样的问题：重数学知识的灌输，轻数学思维的提升、数学思想的感悟，忽视数学文化的教育价值与作用。因此，在出入相补原理教学中，要引领学生品味出入相补原理的数学思想、数学精神，厚植家国情怀，对学生进行品德教养、性情陶冶，让学生在学习数学的过程中感受数学文化之魅力，培养核心素养，从而落实立德树人根本目标和任务。

一、出入相补原理

（一）出入相补原理的由来

几何学体系包括欧氏几何学和中国古代几何学等。欧氏几何即欧几里得的《几何原本》中的几何学内容，欧氏几何的出现标志着数学领域建立了公理化思想体系，为数学几何明确了一种建立科学理论的模式，为人们提供了丰富多彩的几何知识内容。

中国古代几何学形成了一套体现中国古代数学独有风格且生机盎然的系统，它从出入相补原理、容直容横原理、刘徽原理等精炼扼要的原理出发推导数学知识，其中出入相补原理是中国古代数学推导图形面积公式的传统方法和最基本的原理。

中国古代数学家利用“以盈补虚”的割补法，即以多余补不足，图1 中的三角形“上盈下虚，以上补下”，将三角形面积问题转换成长方形面积，从而推导出计算公式。

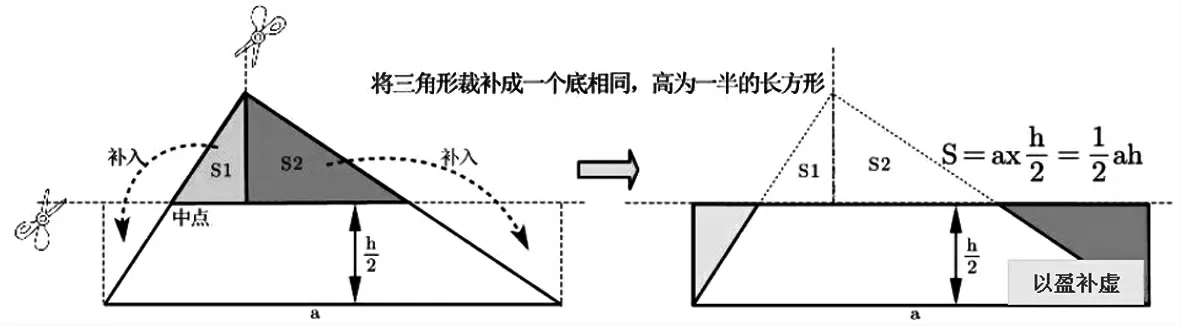
图1 三角形“以盈补虚”割补法

2000 多年前，《九章算术》记载了三角形面积的计算公式，将三角形称为圭田，长方形称为直田。刘徽在《九章算术注》中注解：“半广者，以盈补虚，为直田也”，说明它是应用出入相补原理，由长方形面积导出了三角形面积公式。圭田术曰：“半广以乘正从”得积步[1]。广，称作底；正从，称作高，“圭田术”翻译成现代语言就是说“三角形的面积等于底的一半乘以高”。

《九章算术》方田章中，还给出了用“以盈补虚”的割补法计算梯形面积的两种方法（见图2），即并两邪（上底和下底）而半之（除以二，其实就是线的割补），以乘正从（就是高）若广；又可半正从（高的一半）若广，以乘并（上底和下底的和）。

图2 梯形三角形“以盈补虚”割补法

出入相补一词出自《九章算术注》，刘徽在《九章算术注》对“勾股术”中勾股定理的证明过程作了如下解释：“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不移动也；合成弦方之幂，开方除之，即弦也。”[2]出入相补由此得名。刘徽用出入相补原理解决了一个又一个数学难题，系统地给出了各种图形面积公式的证明。

我国著名数学家吴文俊对出入相补原理作了概括，其内容有四：一是一个几何图形，可以切割成任意多块任何形状的小图形，总面积或体积维持不变，等于所有小图形面积或体积之和；二是一个几何图形，可以任意旋转、倒置、移动、复制，面积或体积不变；三是多个几何图形，可以任意拼合，总面积或总体积不变；四是几何图形与其复制图形拼合，总面积或总体积加倍。

出入相补原理是古代几何学中最基本、最重要的一条原理。它的意思十分直白，简单明了，在逻辑思维上更容易被他人接受，是一个不证自明的常理。研究相关著作可以发现出入相补原理是一个解决实际问题的一般方法，是“无字证明”的工具。

（二）出入相补原理的使用范围

根据吴文俊的理解，出入相补原理适用于平面图形和立体图形。在图形范围中出入相补原理的使用情况也是有不同的，如等腰三角形、直角梯形都可以利用出入相补原理直接论证，而论证圆的面积则需要出入相补原理和极限思想相结合。除此之外，出入相补原理的缺陷也是要特别注意的，它的缺陷就是过于直观化，在操作过程中，图的分、割、移、补都属于直观几何，不小心就容易忽视细节部分，导致结果不一致[3]。

平面图形有直线型和曲线型两种，其中直线型的图形面积往往采用出入相补原理推论，因此可以说出入相补原理在解决能够转换为直线型的图形面积时很有帮助。如解勾股形面积、等腰三角形面积等，都可以通过转化为面积相等的长方形，再运用长方形的面积公式去计算。

立体图形可分为能够经过有限次分割和不能够进行有限次分割成长方体的图形两种，而出入相补原理的作用就是分割直柱体，重新组合成长方体再求体积。其中这个直柱体是一个截面为梯形的立体图形，比如在证明堤、沟、渠等的体积时，可以直接运用出入相补原理将复杂的图形经过有限次割补重合为长方体，再利用长方体体积公式证明而得出结论。

二、小学数学教材中的出入相补原理

人教版小学数学五年级下册教材的“多边形的面积”单元的“平行四边形的面积”一节，把平行四边形拆分并重塑成面积相同的长方形，再通过面积算法推算出平行四边形面积计算公式，见图3。

图3 平行四边形面积公式的推导

“三角形的面积”一节，通过把两个全等三角形“倍拼”，转化为等底等高的平行四边形，从而找到三角形面积和平行四边形面积的关系，推导出平行四边形公式，见图4。

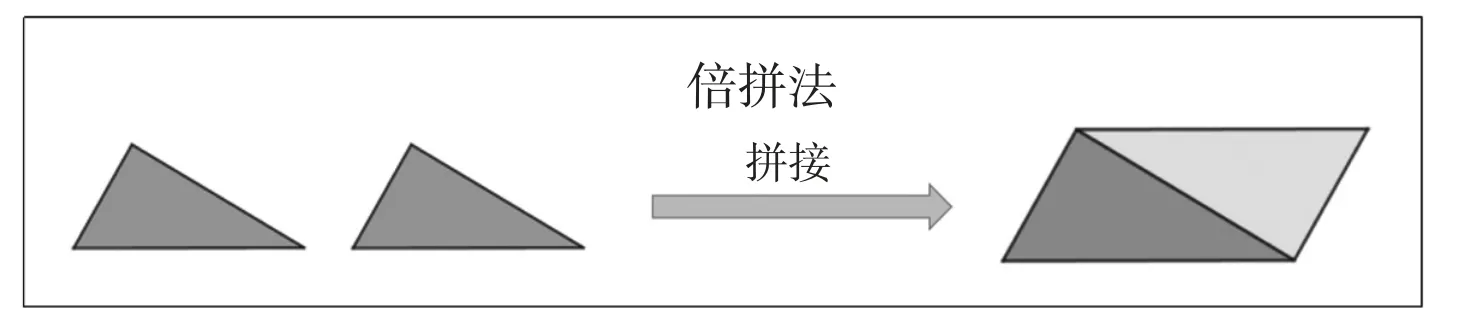
图4 三角形面积公式推导的倍拼法

“梯形的面积”一节，将两个全等的梯形“倍拼”成一个平行四边形，类似推导三角形面积公式，通过梯形面积与拼成的平行四边形面积的关系推导出梯形面积计算公式。可连接梯形两腰中点，将梯形分割成两部分，移补成一个平行四边形，利用出入相补原理，梯形面积就是拼成的平行四边形面积，从而推导出梯形面积计算公式，见图5。

图5 梯形面积公式推导的倍拼法

本单元的“你知道吗？”栏目介绍出入相补原理，将三角形和梯形通过割补转化为面积相等的平行四边形，让学生直观了解出入相补原理的实际运用，见图6。

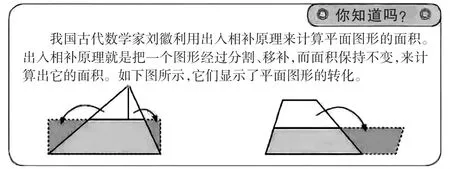
图6 人教版小学数学教材中的“你知道吗？”

出入相补原理是人教版小学数学教材中介绍数学文化的板块，该内容是在学生已经学习并掌握了多边形面积计算公式的基础上进行教学的，为后面学习圆的面积以及中学阶段的勾股定理、球的体积奠定了基础。出入相补原理是中国古代几何中最基本、最基础的原理，在中国数学史上占有极为重要的地位，对后世影响深远[4]。

三、出入相补原理的教育价值

（一）加深学生对图形面积公式的理解

图形面积公式是小学数学的重要内容，很多教师采用“记忆公式+模仿例题+巩固练习”教学，学生对公式知其然但不知其所以然。在教学中采用出入相补原理推导图形的面积公式，可以加深学生对公式的理解。

（二）有利于学生感悟数学思想方法

《九章算术》体现的归纳体系、模型化等一系列的基本思想方法，都属于中国传统的基本的思想方法。出入相补原理作为中国古代几何学最基本的一个原理，其蕴涵的思想方法与《九章算术》体现的思想方法是一致的，有利于感悟蕴涵其中的数学思想方法，提高数学解题能力。

1.化归思想

将一个问题从困难变成复杂，从复杂到简化的过程叫作化归。它是通过问题的转化来解决问题的一种方法。

小学数学教科书阐述了平行四边形、梯形、三角形等面积公式的推导过程，运用了出入相补原理来化归，再求出面积的过程。由此可见，在小学数学的教学中，出入相补原理是推导出平面图形面积公式的重要思想方法，该思想方法运用图形化简的转化，通过新图形的分析使问题顺利解决。

2.数形结合思想方法

数形结合思想方法是将问题中的数量关系转化成大小、位置的关系，或者将数字与位置的关系转换成数量关系，从而使得问题更简单、更直观，可以更好地求解。

刘徽运用出入相补原理将数字与形状之间的关系转换成数字的大小、位置的关系，也就是将数字的大小、位置的关系转换成数字的关系，即数—形—数的转化，从而为中国古代数理中的数字和形状的结合提供了一种特殊的方法。

3.极限思想

极限思想是使变量通过无限过程转化为常量的数学思想，它相比于其他的思想方法更为活跃，是动态的。在小学阶段，极限思想就已出现在教材中。如在求圆形的面积时，将圆形的表面分割成等份的扇形，重新合成的图形近似于一个平行四边形；当继续把圆形多次分割，其表面的扇形大小越来越细，它的数量会不断增加，最终重新组合就会无限接近于一个长方形，再利用长方形的求积公式求出圆的面积。在这里求圆形面积的问题就是运用出入相补原理把圆面积转化为长方形的面积，通过对图形的转化，简明直观地完成极限思想的渗透。

（三）出入相补原理的育人价值

出入相补原理的育人价值主要体现在精神力量价值、美学价值和具体证明应用等方面。

1.精神力量价值

数学学习是一项探索科学知识的活动，数学倡导实事求是的精神。在历史变迁中，数学所表现出的文化精神既是一门学科的现象，也是一种文化现象。在几何学中，出入相补原理贯穿整个理论体系及其发展的始终。其中对平面多边形面积的计算、勾股定理的证明、勾股容方容圆问题、解二次方程和秦九韶三斜求积公式的运算证明过程等等，均说明出入相补原理在古代数学几何中的重要性。赵爽运用出入相补原理，构造“赵爽弦图”证明了几何学中著名的勾股定理；刘徽用“割圆术”推导出“圆的周长的面积公式”；祖冲之父子用出入相补构想“牟合方盖”推导出球的体积公式，形成引领世界的数学成果。可见，出入相补原理是中国古代数学家的智慧结晶。同学们学习运用出入相补原理，有利于弘扬中国古代数学的优秀文化，发扬中国古代数学家的“刻苦钻研”和“求真创新”精神，自觉树立爱国报国的理想信念。

2.美育价值

数学之美是客观存在的，数学的美包含简约之美、和谐之美、奇异之美，等等。出入相补原理的美在中国文化中得到了充分的体现，《韩非子·初见秦》载“今秦地折长补短，方数千里”[5]。将土地分割、重新割补成形状规则的正方形，以估计土地面积大小，这一做法就是出入相补原理的运用。除此之外，《老子》《孟子·滕公文上》《战国策·秦策一》中也有运用出入相补原理的记载。在古代文学中，富含几何学的语句也体现了出入相补原理的简约美。如在讲解唐代诗人宋之问的《灵隐寺》时，教师可以“楼观沧海日，门对浙江潮”作为基础，变换成几何图像，解释和梯形有关的知识。通过学习，可以激发学生的好奇心，使他们感受数学的美和神奇。

四、出入相补原理及其育人价值在教学中的实现

（一）实现方法

1.结合教材在课堂中应用

在教学中，数学史的融入是不能缺失的，在教学中教师应结合出入相补原理的内容渗透数学史的知识，让学生感受数学文化的魅力。教师讲授数学史知识时宜围绕几个方面展开：首先，介绍数学成就。教师可在合适的教学节奏中介绍出入相补原理的概念和内容。比如在讲解多边形面积时可以介绍出入相补原理的概念和《九章算术》里的相关知识，让学生了解古代数学家在多边形面积求解上取得的成就。其次，古今解法的对比。在学习勾股定理时，可以介绍我国古代数学家运用出入相补原理证明勾股定理的方法，再与所学的解法对比，让学生体会多种解法的魅力。再次，注重实例归纳。在教学中先不明确讲解出入相补原理的内容和含义，而是通过讲解实例，由学生自己推导出结果。如前所述，在求平行四边形、三角形、梯形的面积时，先运用分割、移补、“倍拼”等方法推导出结果，再点出出入相补原理。注重实例归纳有利于锻炼和培养学生的思考能力。

2.在课外活动中应用

可以充分利用课外活动实现出入相补原理的育人价值，课外活动形式主要包括专题讲解和趣味宣传两种。专题讲解是由数学兴趣小组的“小讲师”以出入相补原理为专题，向全班同学介绍出入相补原理的内容、历史背景及在我国古代运用的事例等。学生通过查阅资料，直接接触了解出入相补原理，从而激发了学习兴趣。趣味宣传是由数学兴趣小组利用黑板报等学生喜闻乐见的形式介绍出入相补原理的史料、图形，让学生了解出入相补原理。

（二）实现途径

1.探寻图形转化之理，感悟数学思想方法

基于深度学习的“说理”课堂，我们需要进一步探寻知识背后的道理。“出入相补”目的只有一个，就是把未知转化为已知，“化归思想”就是这一系列“以盈补虚”割补法背后的最重要的数学思想。转化方法是教学多边形面积一课的关键，学生进行剪拼方法的操作后，在对比观察中发现形状变了但面积没有变这“变中有不变”的数学道理，进而在转化的前后对比中感悟其中的“变与不变”和“等积变形”的数学思想。例如，在梯形面积公式推导的教学中，运用源自我国古代几何学的出入相补原理的剪拼法和分割法推导梯形面积公式。“分割”即把一个梯形剪成两个或两个以上已学过的图形，“拼补”即通过移补把一个图形转化成已学过的图形，最终都要具体到探究前后两个图形之间的关系。从解决问题的角度看，重点是让学生自主寻找求出梯形面积的办法，感悟数学思想，这与课标解读的“说理”要求是相吻合的。

2.追古溯今，提升学生的数学文化素养

在教学中融入数学史，弘扬中国古代数学的辉煌成就，可以增强学生的民族自豪感，从而体现育人价值。将我国古代数学家刘徽提出的“以盈补虚”和“出入相补”的原理融入“多边形面积”教学中，能让学生在把握与理解知识的层次上有更深入的思考。

教材中多边形面积公式推导过程中使用了两种方法：古希腊欧几里得在《几何原本》中提出来的“倍拼法”和中国古代数学家刘徽于《九章算术注》中提出的“出入相补法”。教师可比较这两种方法在解决小学数学教学中经常出现的“求阴影部分面积”问题，让学生感受出入相补原理的优越性。我国古代数学家刘徽运用出入相补原理，将圆分割移补成长方形来推导圆的面积公式；古代数学家赵爽运用出入相补原理构造“勾股圆方图”，用“最省力”的方法证明了勾股定理；祖暅用出入相补原理构成了“牟合方盖”，把平面上的出入相补推广到空间上的出入相补，推导出球体体积计算的公式。这些成就，反映了中国古代数学家的聪明才智与钻研精神，是中国古代数学文化的骄傲。

3.使用信息化教学工具呈现数学之思，欣赏数学之美

教学中，使用计算机软件“几何画板”直观演绎三角形和梯形面积的推导过程，可以活跃学生的思路，提高思维的灵活性，使学生在潜移默化中掌握转化的思想方法。学生通过观察动态的几何画板课件，寻找图形的联系，发现“变与不变”，可感悟“变化中不变”的数学思想，欣赏守恒之美。