基于蒙特卡罗法硬膜血肿厚度计算的数值仿真研究

范鑫燕，罗海军，2，李妍妍，向 洋，罗 霞，覃 睿，郭 盼

（1.重庆师范大学光电功能材料重庆市重点实验室,重庆 401331；2.重庆国家应用数学中心,重庆 401331）

1 引言

硬膜出血是创伤性脑损伤中最常见也是最严重的二次损伤病变，致死率30%～40%，致残率接近100%［1］，其中病变位置多发生于颅骨下方脑脊液中，出血量可在几小时内堆积形成血肿，血肿扩大可能引起脑中风、神经病理恶化［2］等后遗症，导致永久性精神疾病甚至危及生命.目前医院评估硬膜血肿是采用计算机断层扫描（Computed Tomography，CT）和磁共振成像（Magnetic Resonance Imaging，MRI）等检测精度高的大型精密设备，但CT 与MRI 价格高、体积庞大，不适用实时连续监测，且往往伴随着一定的电磁辐射，不适用重度患者、婴幼儿和孕妇等［3］.

近红外光谱技术（Near Infra-Red Spectroscopy，NIRS）作为监测神经创伤主流的非侵入式辅助手段，是基于生物组织结构的光谱分析，其典型的应用是检测颅内占位血肿［4］.光谱600 nm～950 nm 波段是人体组织的“光学窗口”，该波段光可穿过脑部组织几厘米深，皮肤、骨骼等组织作为均匀介质呈现出散射系数大，吸收系数小的特性，血液对于该波段内的近红外光敏感［5］，血肿含有丰富的血红蛋白，呈现高吸收的特性，对光能量吸收强度是周围正常脑组织的十倍以上，分析光的衰减信息可得到血肿层信息［6］.20 世纪末美国宾夕法尼亚大学的Chance B［7］等将NIRS 用于脑血肿检测的研究，Salonia 等人对儿童脑出血检测进行了研究［8］，国内军事科学院张彦军利用筛选器建立血肿吸收系数预测模型对血肿厚度进行判断［9］，天津工业大学王金海团队采用多通道差分吸光度法检测脑异物［10］，各研究表明NIRS 可用于颅脑血肿检测.为实现硬膜血肿的快速检测与厚度评估，本研究基于NIRS 与蒙特卡罗模拟（Monte Carlo，MC），结合数值分析提出一种预测硬膜血肿厚度的数学方法，即在正向测量光子信息的基础上，构建不同检测距离下的函数模型，建立逆向函数矩阵，该方法的优点是充分考虑到了检测器的分布和硬膜血肿对光传导的影响，从定量的角度分析血肿对光衰减的影响，能够获得一种通过颅脑表面光子信息求解硬膜血肿厚度的方法.

2 理论原理与模型建立

2.1 蒙特卡罗理论

颅脑结构中脑组织（灰质与白质）为不规则形状的起伏层，目前没有统一认可的解析式方案，复杂组织的灵敏度和穿透深度依赖于数值解决办法［11］.MC 是一种描述光在生物组织传播的经典数值模拟技术，其优势在于不需要设定光子传播的解析形式、复杂的边界条件，因此不会被扩散和其他近似方程所偏置，被认为是光在组织传播的“金标准”［12］.MC模拟传播示意如图1所示.

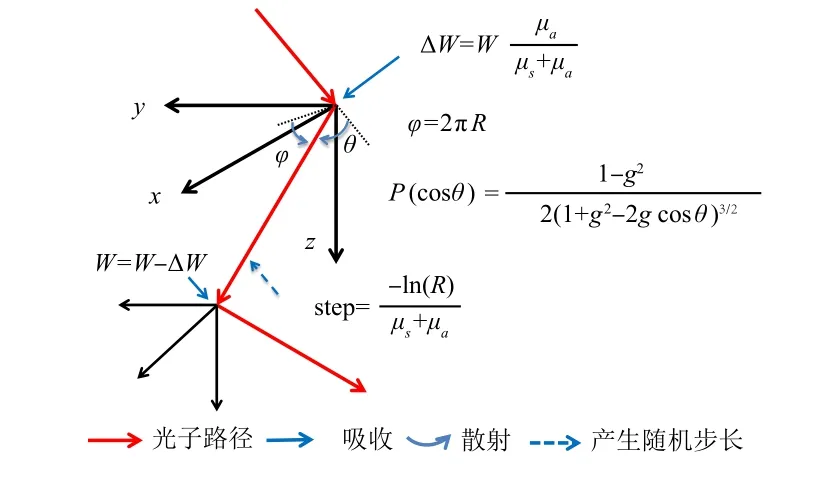
图1 蒙特卡罗模拟传播示意图

光子以权重进W=1 入组织，产生随机步长step，每产生一个新步长都会发生吸收，散射.在传播过程中，吸收导致光子权重衰减，散射会改变光子传播方向，直至光子透射出组织表面或权重衰减至足够小的值，光子则被定义为死亡，之后光源再发射一个新的光子进入组织.其中R为（0～1）随机数，（θ，φ）分别为坐标系下极角与方位角，决定光子散射的方向；step为随机步长，由一个（0～1）随机数和吸收、散射系数决定；ΔW为在该步长内组织对权重的吸收量，由组织的吸收和散射系数决定.记录所有光子的传播信息，便可模拟出光在组织里的传播过程，如图2 所示，图2 表示源-检测距离（Source Detection，SD）=1.5 cm 部分光子传播路径x-z轴截面图.

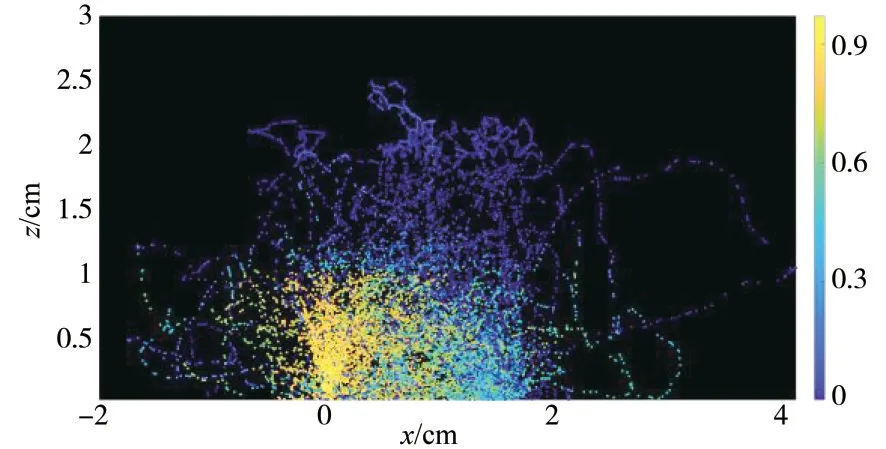
图2 x-z轴平面

其中图例代表光子权重，可以看出，特定检测距离下的光子传播路径截面呈现“香蕉”型，光子路径越远，权重衰减的越多.

2.2 颅内血肿建模

硬膜血肿为多发外伤性颅内血肿，颅内出血堆积形成血肿块，血量扩散引起血肿厚度变化，位置信息未变，故本研究选用血肿厚度作为研究对象［13］，硬膜出血多发位置位于颅骨层下方的脑脊液层，为了更好的模拟人脑的光学特性，根据人脑的结构，本研究颅脑结构分为五层，从外到内依次为头皮、颅骨、脑脊液、灰质和白质.血肿模型中将脑脊液层替换为血肿层，模型结构如图3所示.840 nm波段处，血红蛋白较其他组织对近红外光的吸收高出10倍以上，故本研究选取840 nm为光源的波长，设血肿厚度为d，空气折射率n=1，参数［14］如表1所示.

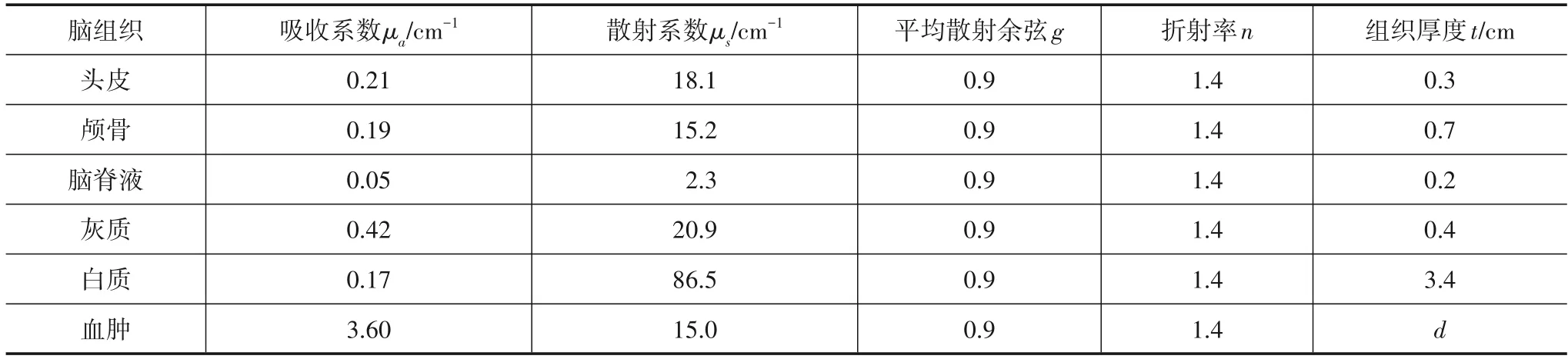
表1 头部模型在波长为840 nm的光学参数

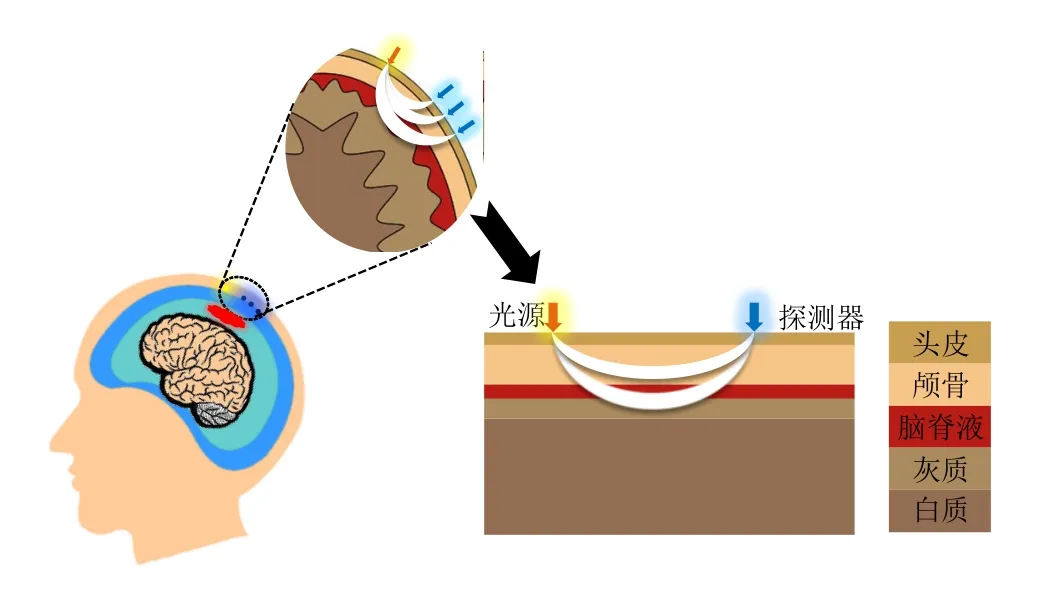
图3 颅脑血肿模型图

2.3 仿真模型验证

本研究采用自编蒙特卡罗程序MC自编，为验证程序的准确性，采取两种模型的模拟结果与其他研究者的蒙特卡罗程序模拟结果相对比.

模型A：有界组织模型，组织厚度t=0.02 cm，折射率n=1，μa=10 cm-1，μs=90 cm-1，g=0.75，每次模拟50 000个光子，进行5 次计算取平均值.程序计算总漫反射率Rd与总透射率Tt，计算结果与汪立宏MCML（Monte Carlo Multi-Layered）［15］、范德哈尔斯特（van de Hulst）［16］，普拉尔（Prahl）［17］的数据进行比较，以MC 仿真结果Rd、Tt数据为基础，计算与其他研究学者仿真结果的误差率，计算如式（1）所示，仿真结果如表2所示.

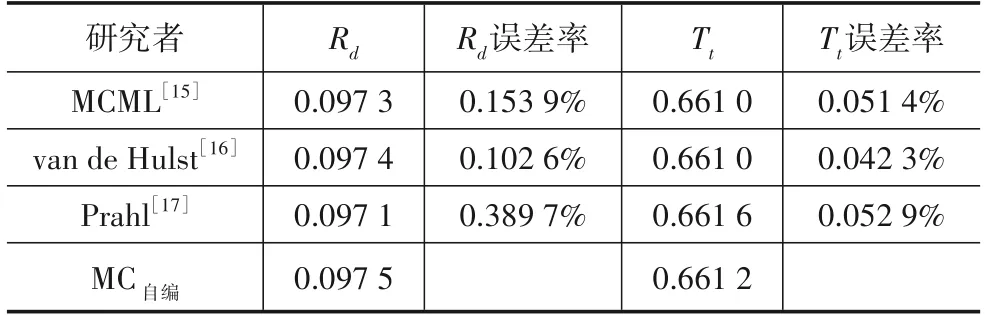
表2 模型A对比数据

模型B：半无界组织模型，μs=90 cm-1，n=1.38，t=10 000 cm，g=0.75，μa取0.5 cm-1、1.0 cm-1、1.5 cm-1、2.0 cm-1、2.5 cm-1，每个吸收系数模拟50 000 个光子，进行3 次计算取平均值与汪立宏MCML 程序计算结果进行比较，对比结果如图4所示.

表2 数据显示自编程序有界介质Rd、Tt仿真结果较其他研究者误差均＜0.4%，图4 显示半无界介质模型的数据曲线几乎重合，最大误差0.002 23，最小0.000 21.该对比数据表明本研究的程序数据可靠，可以正确的表达光在生物组织里的传播.

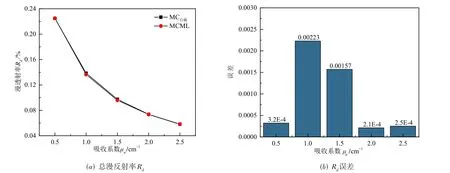
图4 模型B与MCML对比结果

本文采用的MC自编程序，相较于MCML，自编MC可以追踪光子在组织里的路径，记录光子的实时位置及衰减权重，可以记录特定检测器内光子信息，更准确的分析光在组织里的传播情况.

3 结果与分析

3.1 仿真结果正向分析

仿真模拟从坐标原点（0，0，0）发射107个光子，在光源横向位置设置9 个检测器，SD≤5 cm，检测器半径为0.2 cm，收集每个检测器的光子数量，定义源-检测器灵敏度（Source-Detector Sensitivity，SDS）如式（2）所示：

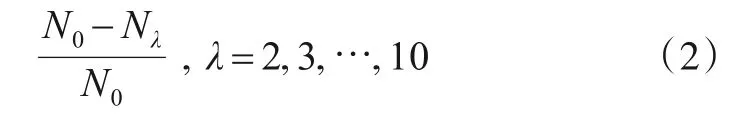
其中N0为正常脑组织检测的光子数，Nλ表示d=0.2 cm，0.3 cm，…，1.0 cm 情况下检测器检测的光子数，仿真结果如图5、图6所示.

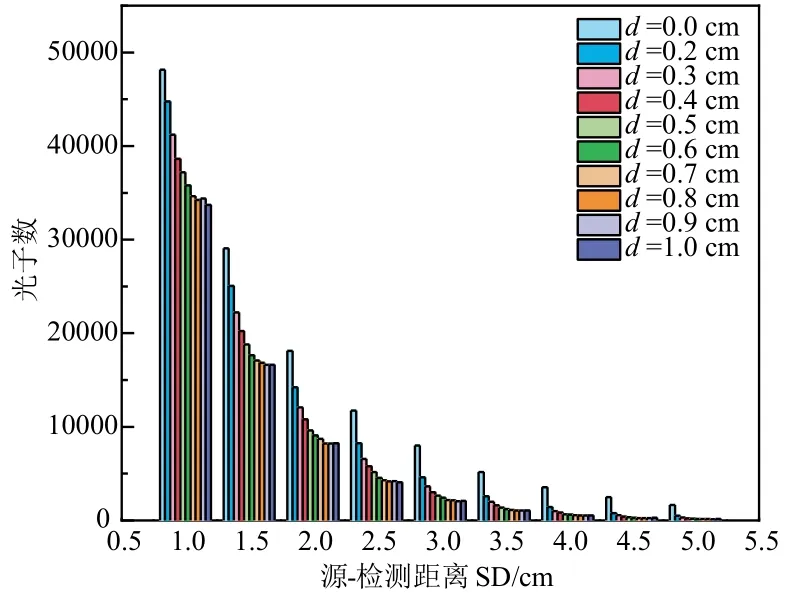
图5 模型仿真下的光子数据

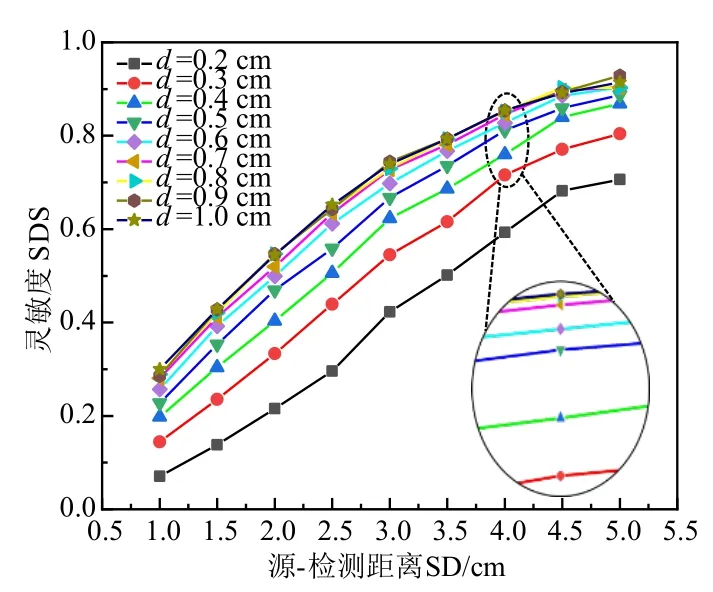
图6 不同血肿厚度下的SDS

由图5 可得，血肿厚度、SD 与光子数具有相关性，光子数与SD 的数值关系呈现指数下降的趋势，d=0 cm与d=0.2 cm，0.3 cm，…，1.0 cm有明显的光子数差量值，因此可以有效区分是否含有血肿.由图6 可以看出SD与SDS 存在相关增长趋势，SD＞4.0 cm，SDS 上升速率减缓且趋于平稳，验证图2 的结论，SD 增加伴随权重与光子数的衰减，对获得目标层信息贡献不大，数据偶然性将会增大.d＞0.8 cm，SDS 之间差值缩小，曲线基本重合，说明入射的大部分光子已达到了组织最大的有效深度，血肿厚度增加对获得血肿层的信息意义不大.

3.2 数据分析及求解

MC 仿真的正问题是已知颅脑组织的参数、血肿位置及厚度信息，研究颅脑表面场域检测器内的光子分布特性；逆问题即对颅脑中是否含有血肿以及血肿厚度进行有效预测.MC 正问题仿真得到的数据是理想与无测量噪声的，因此预测模型采用仿真数据.逆问题分析中，为了得到低误差的预测值，采用控制变量法可通过对已知量的了解来减少对未知量估计的误差.

由SDS 可知检测器得到的光子数据，能够有效反映血肿改变的差异，之间的三维关系如图7 所示，整合检测器光子数与SD、血肿厚度的函数关系，是评估颅内血肿厚度的关键.

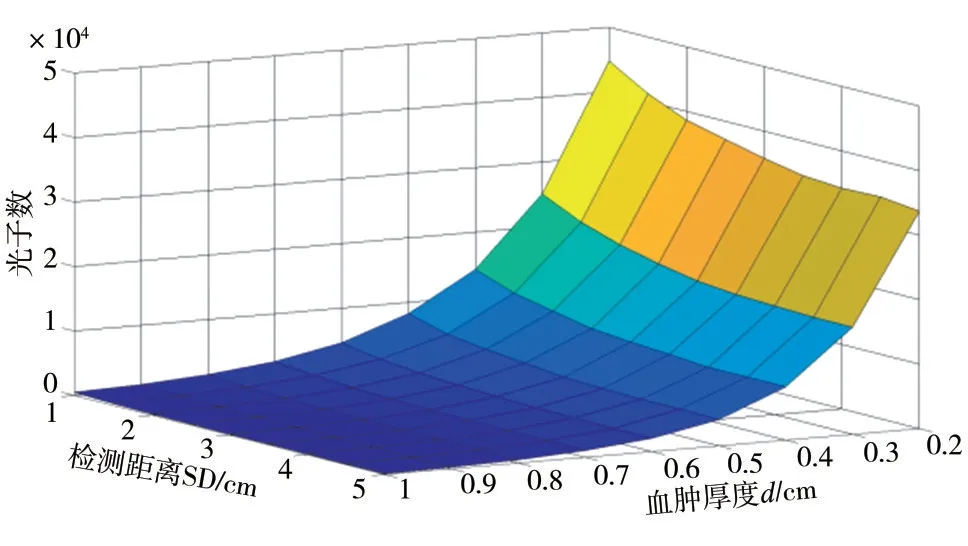
图7 血肿厚度、SD与光子数三维关系图

图7显示，光子数与SD、血肿厚度具有相关性，设D为光源横向放置的检测器，光子数矩阵函数N与检测器的关系如式（3）所示：

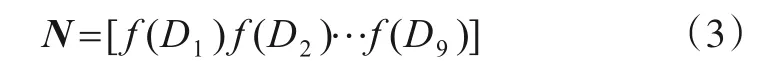
血肿厚度增大，光子数有明显的下降趋势，为了更直观，准确得到血肿层对光的衰减情况，设血肿厚度为变量x，h（x）为血肿厚度与检测器有关光子数的函数关系式，f（Di）与h（x）存在以下关系：

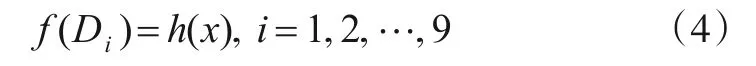
构建h（x），即构建正向函数方程组，本研究根据h（x）的趋势选取两种函数模型.

函数模型1：幂律衰减模型，可以通过异速关系从光与血肿组织的相互作用模型中导出［18］，表达如式（5）所示：

其中，η为比例系数，u为标度指数，由自变数P的数值决定，利用最小二乘法得到最优拟合变量［19］，求出残差平方

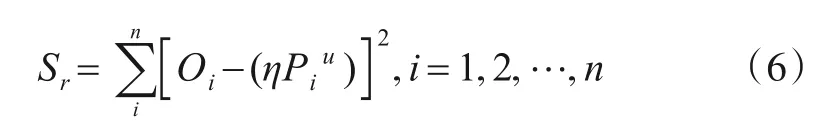
Sr对η，u求导，使导数等于0，解方程组，可求解η，u.

函数模型2：指数律衰减模型，可通过血肿厚度的变化和光衰减作用关系得出［20］，表达如式（7）所示：

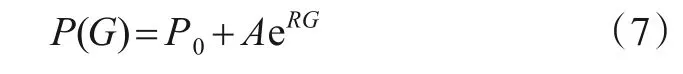
其中，P0为补偿系数，A为前置因子，R为衰变速率，采用LM（Levenberg-Marquardt）优化算法进行非线性曲线拟合［21］，求出残差平方

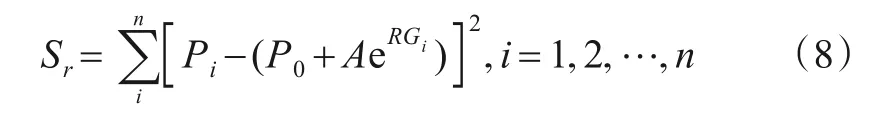
将P0、A，R作为变量，使得Sr最小可求得P0、A，R.

将h（x）代入两种函数模型中，以Pearson's R、RSquare（COD）作为函数构建的指标，Pearson's R 表示变量间线性相关的程度，R-Square（COD）表示依变数未知量的变异中占据的百分比，由控制的自变数来解释.上述SDS可知d＞0.8 cm，大部分入射光子已经达到了最大的有效深度，透射到检测器光子数之间的差值很小，为提高模型的精确度，在构建模型时将不考虑d＞0.9 cm的数据，两种函数模型构建结果如表3所示.

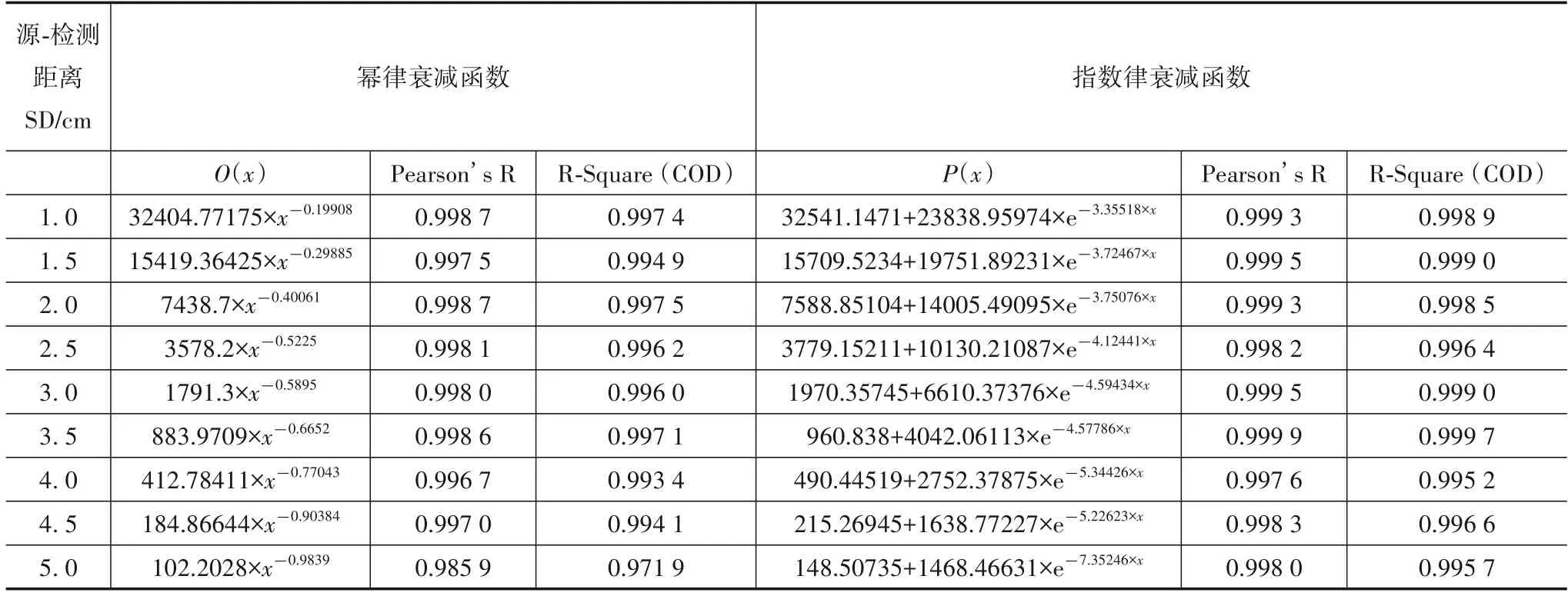
表3 正向函数方程组

表3 可得，SD＜5.0 cm，两种函数模型Pearson's R、R-Square（COD）均＞0.99，SD=5.0 cm，幂律衰减函数模型的Pearson's R、R-Square（COD）＜0.99，到达颅脑头皮的光子数变少使数据具有较大的偶然性.Pearson's R、RSquare 显示，函数矩阵构建有效，SD≤5.0 cm，两种函数组模型可以表达光在颅脑组织里传播.

以上结果显示，已知血肿层厚度信息，可通过函数矩阵正向求解检测器的光子信息，分析光在血肿层的传播情况.为了通过检测判断颅脑中的出血情况，本研究基于正向函数矩阵模型构建逆向函数矩阵，为验证两种函数模型的正确性，本研究选取d=0.25 cm，0.35 cm，0.45 cm，0.55 cm，0.65 cm，0.75 cm 进行仿真验证，光子数为107.将不同血肿厚度检测到的光子数代入函数矩阵中，求解x，x平均值与平均绝对误差如表4、表5和图8所示.

图8（a）显示预测值与参照值十分接近，血肿厚度＜0.7 cm，幂律衰减模型与指数律衰减模型的预测值与参照值曲线几乎重合，两种函数模型平均绝对误差＜3.6%，血肿厚度＞0.7 cm，两种函数模型与参照值误差增大.表4、表5 得，幂律衰减模型计算值最大误差0.010 752，最小误差0.001 160，最大平均绝对偏差6.473%，最小为1.13%；指数律衰减模型计算值最大误差0.046 886，最小误差0.000 316，最大平均绝对偏差10.777%，最小为0.981%，两种函数对比结果在有效误差范围内.

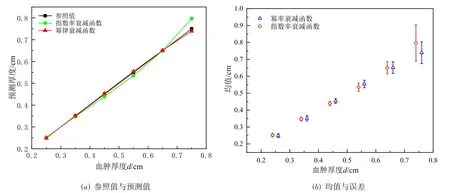
图8 结果对比分析

表4 幂律衰减函数验证结果

表5 指数律衰减函数验证结果

图8（b）显示，幂律衰减模型在误差，平均绝对误差以及标准差都要比指数律衰减模型数值小，血肿厚度=0.75 cm，幂律衰减模型平均绝对误差比指数律衰减模型＜4.3%，误差＜6.3886%，预测平均值更接参照值，构建效果更好，选择幂率的衰减模型可以更好表达血肿层的衰减信息，可作为颅脑血肿厚度求解的函数模型.血肿厚度与误差具有相关性，这是因为在相同模型下光子在组织里的路径增加，能量衰减逐渐增多，透射出头皮组织表面的光子数量减少，导致误差变大.

4 总结

NIRS 与MC 可模拟光在正常颅脑组织与含有血肿的颅脑组织中的传播过程，采用控制变量法改变血肿厚度，对模型正向仿真，提出血肿检测及厚度预测的逆问题可行性分析方法，分析血肿厚度与SDS，结果显示该方法可以有效检测颅脑是否含有血肿，检测灵敏度与检测距离存在对数相关性.利用仿真数据建立幂律衰减模型与指数律衰减模型的正向方程矩阵，可以有效表达光在血肿层的传播情况.逆向函数矩阵的预测值与参照值的对比显示，在标准差、平均绝对误差以及预测值等方面，幂律衰减模型比指数律衰减模型更精确，可作为预测并评估血肿层厚度有效数学工具.