多目标同时取送货选址-路径问题的多起点变邻域搜索算法
陈希琼,胡大伟,王 宁
(长安大学运输工程学院,陕西西安 710064)
1 引言
选址-路径问题(location-routing problem,LRP)集成处理设施选址和车辆路径两个关键物流决策问题.传统LRP 研究的车辆路径问题(vehicle routing problem,VRP)中,客户仅存在取货或送货单一需求,而现实物流系统中,通常存在需要同时提供送货和取货服务的客户,且要求在访问中同时完成取送货,如:需要回收空瓶的饮料、鲜奶及啤酒配送.
针对所有需求点均有取送两层需求的物流配送问题,Min[1]首次定义了考虑同时取送货的VRP(VRP with simultaneous pickup and delivery,VRPSPD),研究中心图书馆与地方图书馆之间图书发送与回库问题.之后VRPSPD被广泛研究:如多车场VRPSPD[2]、不同车型VRPSPD[3]、带时间窗VRPSPD[4-5]、时间依赖型VRPSPD[6]等,以环保为出发点研究低碳约束[7-8]和最小化燃油消耗[9]的VRPSPD引起诸多学者的兴趣.陈希琼等[10]研究同时考虑车辆容量和距离约束的VRPSPD双目标模型,并采用蚁群算法进行求解.
VRPSPD的广泛研究表明考虑同时取送货在物流决策中的重要性,然而考虑同时取送货的LRP(LRP with simultaneous pickup and delivery,LRPSPD)近期才开始被少数学者关注.Karaoglan等[11-12]最早提出LRPSPD并进行了持续研究,构建了其初始模型,先后采用分支切面法、混合遗传算法求解该模型;随后,提出了基于节点和基于弧的混合整数规划LRPSPD模型,构造了LRPSPD测试算例集,并设计两阶段模拟退火算法[13]和模因算法[14]求解模型.Yu等[15]设计多起点模拟退火算法,基于文献[13]构造的算例,求解LRPSPD;在进一步研究中[16],额外生成了客户数达318的4组算例,设计改进的模拟退火算法进行求解.孙青伟等[17]基于实际案例研究了多车型LRPSPD.Kartal等[18]研究单一指派p-中位转运站LRPSPD,Karimi[19]对枢纽选址VRPSPD 进行研究,不同于传统LRPSPD,文献[18-19]允许枢纽间转运.Fan等[20]基于构造算法、局部搜索和变邻域算法提出多起点混合启发式算法求解两阶段LRPSPD;郭放等[21]研究前置仓选址VRPSPD.
文献中考虑同时取送货的多目标优化研究主要针对VRPSPD,几乎不能找到LRPSPD多目标优化研究.Garc´ıa-N´ajera[22]对取送货问题的多目标研究进行调查,指出工作量平衡目标应被考虑,但在其提出的六目标模型中并未包括工作量平衡目标.同时,多目标优化求解复杂,由于对多目标进行转化处理具有不能兼顾多个目标的局限性,但近年来同时兼顾多个目标的Pareto解集成为研究重点,如Anderluh等[23].
LRPSPD研究通常以最小化总成本为目标,然而现实运作中决策者需要根据其他可能的情况进行决策,如考虑客户满意度、碳排放、各车辆的工作量平衡等.本文在文献[10]的基础上,集成选址决策,考虑车辆容量和车辆行驶里程约束,建立以最小化总成本与最小化各路径间最大长度差为目标的双目标模型,该模型为文献中首次最小化总成本,同时以平衡各车辆的工作量为目标的多目标LRPSPD研究.鉴于变邻域搜索算法在求解组合优化问题中较好的性能,本文构造四类邻域结构设计多起点变邻域搜索算法,并设计多蚁群构造多个初始解作为变邻域搜索的多起点,对文献中的LRPSPD算例进行求解分析.
2 问题描述和数学模型构建
2.1 问题描述与符号说明
定义图G(N,A),其中NN0∪NC,N0,NC分别表示车场集合、需求点集合.每个潜在车场k ∈N0有固定的开放与营运成本fk,容量为Ck,每个客户i的取送货需求分别为pi,di.假定车场有足够可供派遣的完全相同的车队,每辆车最大容量为Q、最大行驶距离为L,派遣每辆车的固定成本F.每辆车从车场出发,通过恰当的行驶路线有序访问该线路上的所有客户,然后回到车场,每辆车最多执行一条路径的服务.A{(i,j):为边集,每条边(i,j)∈A的行驶成本即距离为cij.本文研究的LRPSPD可描述为:从一系列潜在车场中选择开放的车场,并从开放的车场派出车辆,在不超过车辆容量和最大行驶里程的约束下,找到服务所有客户后回到原车场的路径,使成本最小化,同时最大可能地平衡各路径的总长度(即最小化最长路径与最短路径的里程差).双目标LRPSPD模型中的变量定义如下.
决策变量:xij1表示先后连续访问客户i,j,否则xij0;yk1表示备选车场k被选中开放,否则yk0;zik1表示节点i分配给车场k,否则zik0.
其他变量:Yij表示在(i,j)上时装载的送货量;Zij表示在(i,j)上时装载的取货量;li表示访问客户i时的累积行驶里程;tLmax(min)表示最长(最短)的被派遣车辆行驶路径长度.
2.2 模型构建
基于以上问题描述与符号,构建以下双目标LRPSPD数学模型:
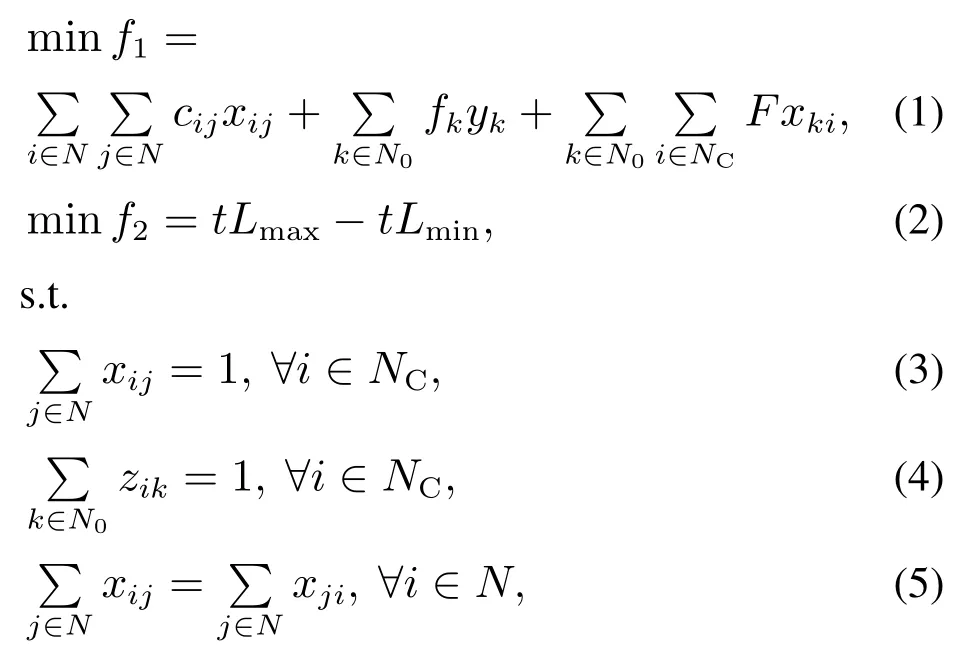
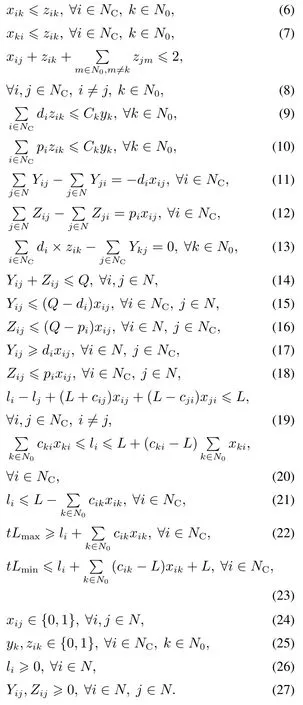
目标函数(1)使总成本最小,包括路径成本、车场的开放与运营固定成本和派遣车辆的成本,目标式(2)最小化车辆的最大行驶里程差,以平衡各车辆的工作量.式(3)-(4)规定所有客户均被分配给开放的车场且仅被访问一次,约束(5)保证进入某客户的弧总数等于从该客户出来的弧总数,约束(6)-(8)消除了未始于车场或止于车场的子路径,且当且仅当分配给相同的车场时,才有可能被连续访问,式(9)-(10)为车场容量约束,式(11)-(12)为访问客户点前后的流量平衡约束,同时表明客户的需求在一次访问中全部满足,约束(13)保证从某开放车场运出的装载量等于分配给该车场的所有客户的送货总需求,约束(14)保证在任意弧上的装载量均不超过车辆容量,约束式(15)-(18)是对上下界进行限定,约束(19)-(21)保证车辆运送距离不超出最大可行驶距离,且当且仅当车被派遣时才存在累积行驶距离;式(22)-(23)界定了车辆行驶路径的长度,式(24)-(27)为各变量的取值约束.
通常,有效不等式的加入可缩紧模型约束,从而消除模型解空间的无效片段.式(28)为式(14)的有效替换,其中M为极大常数,该式表示当且仅当客户被连续访问时,弧上存在流量,且不超过车辆的最大容量.

3 多起点变邻域搜索算法
由于双目标模型并不存在绝对的最优解,因此本文设计优化算法求解模型Pareto解.变邻域搜索(variable neighborhood search,VNS)作为一种元启发式方法已被成功应用于解决多种优化问题,尤其对于大规模组合优化问题效果较好.VNS求解性能受初始解影响较大,因此本文构造有一定关联的多个初始解,并基于各初始解进行变邻域搜索,称为多起点变邻域搜索算法(multi-start VNS),算法流程如图1所示.分步说明如下:

图1 多起点变邻域搜索算法流程图Fig.1 Flow chart of mmulti-start VNS
步骤1初始化VNS产生可行解及不可行解的次数nF0,nINF0及多起点数nMS0,并分别设定其最大值;
步骤2分别基于选址蚁群、分配蚁群及车辆路径安排蚁群构造初始解;
步骤3从初始解的多个邻域中随机选择一个邻域结构进行搜索;
步骤4检查产生的邻域解是否为可行解.
若不可行:则nINFnINF+1并判断生成不可行解的次数是否达到最大,否则回到步骤3,是则跳到步骤5;
若可行:则判断该可行解是否为Pareto解,若是则产生了多目标问题的新解,本轮搜索结束,初始化nF0,nINF0,开始新一轮搜索,回到步骤3;
若不是Pareto解,则nFnF+1并判断是否满足达到最大可生成可行解次数,回到步骤3或转步骤5;
步骤5判断是否达到最大起点数:若nMSnMS+1否则同时更新各蚁群信息素矩阵,回到步骤2;若是则输出并结束程序.
根据以上步骤说明,变邻域搜索的每一个初始解(起点),均在每一次迭代开始时,基于此前迭代产生的解以及更新后的信息素由多蚁群算法产生,从而使变邻域搜索的多个起点间相互关联,且随迭代发生变邻域搜索的起点对应的解更优.
3.1 多蚁群构造算法初始解
蚁群算法最初被Dorigo等[24]应用于旅行商问题(travelling salesman problem,TSP),取得了很好的应用效果.本文将LRPSPD分解为选址、分配、路径选择3个子问题,采用多蚁群算法思想,设计对应的3个蚁群,以构造LRPSPD变邻域搜索初始解.
3.1.1 选址
第s次构造初始解时,ps为开放车场的数量,表示车场k上的信息素强度,Us为还未被蚂蚁选中的车场集合,ηk为表达车场k特性的效用函数.首先根据式(29)确定需开放的车场数,后根据式(30)-(31)所示准则依次选出合适的车场,q为[0,1]的随机数,q0为[0,1]间预先设定数,参数α表示ηk相对于信息素对转移概率的影响程度.

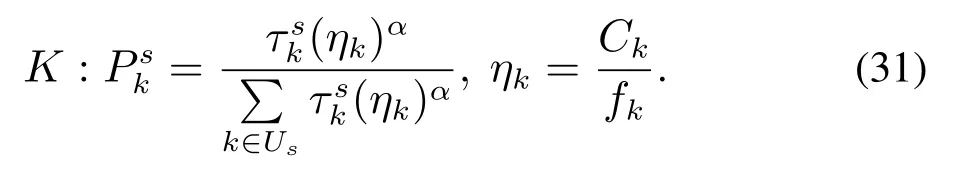
3.1.2 分配
第s个初始解构造过程中,开放的车场k与客户i之间的信息素为,对当前还未分配的任意客户i,根据以下准则从开放的车场Os中选择车场k,并将客户i分配给车场k.

其中:φik为行驶成本的倒数,表示将当前客户分配给行驶成本较小的车场;φik为Φik的倒数,Φik表示为包含当前需分配的客户的条件下,当前已分配给车场的所有客户总取送货的平衡,为包含当前客户的所有已分配给车场的客户集合,q′为[0,1]的随机数,为[0,1]间预先设定数,参数β和γ分别表示φik与φik相对于信息素对转移概率的影响程度
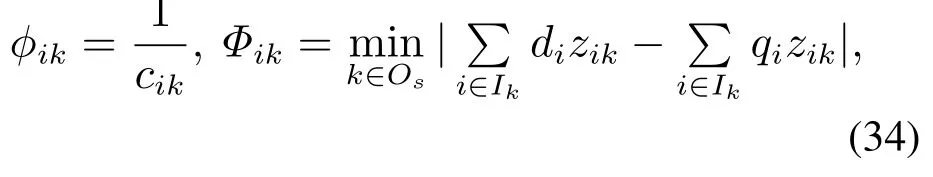
分配结束后,检查分配给各车场的所有需求点总需求是否超出车场容量,并对分配给容量超出的车场的需求点进行调整,调整方案伪代码如下.
算法1:

3.1.3 路径选择
选址、分配确定后,LRPSPD可视为多个单车场的VRPSPD,该节分别确定分配给同一车场的需求点的访问路径.为构造第s个初始解时弧(i,j)上的信息素强度,蚂蚁根据各条路径上的信息量和反映网络本身特性的效用函数决定下一步要转移的点,Pij表示蚂蚁由节点i转移到节点j的概率.其中q′′为均匀分布在[0,1]上的随机数,为预先设定的值,当q≤q0时,蚂蚁直接移动到使效用函数取最大值的点j如式(35),否则按式(36)所示概率进行轮盘赌选择转移到j点,越大表明蚂蚁随机性越小,Zis表示第s次初始解蚂蚁到达节点i上时未访问的节点集合,当达到行驶距离约束或容量约束条件时,返回车场,并再次从该车场开始构建新的路径,直到所有节点都被访问,即

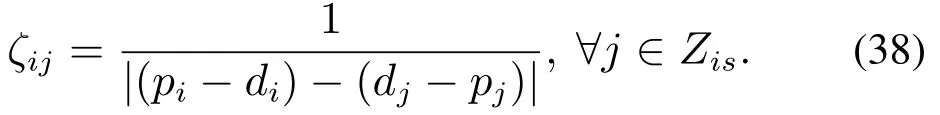
式(38)中当点的净装载量等于点的净卸载量时ζij1.ψij与ζij体现网络本身特征,结合蚂蚁转移规则反应出蚂蚁具有偏好以最大节约距离服务取送货需求差最小的客户的特性.参数β′和γ′分别表示ψij与ζij相对于信息素对转移概率的影响程度.
3.2 多目标变邻域搜索
本文变邻域搜索采用四类邻域结构:路径内点序列操作、路径间点序列操作、从不同车场出发的两条路径交换、开放车场与未开放车场交换.每次邻域操作均在随机选择的扰动机制下被执行,且均以找到Pareto解为目标,变邻域搜索过程定义了最大无效操作次数(产生不可行解次数nINF-max、产生可行但为支配解的次数nF-max),即若产生nINF-max个不可行解或nF-max)个支配解后,仍未找到新的Pareto解,则搜索结束;若找到新的Pareto解,则初始化nINF0,nF0,继续执行变邻域操作.以下为第s次迭代中多目标变邻域搜索操作伪代码.
算法2:


3.2.1 路径内操作
1) 插入:随机选择路径上的需求点子序列σ,从当前位置删除,插入到该路径的其他位置,|σ|小于该路径上总需求点个数.如图2中a所示.
2) 交换:随机选择路径上两个不重叠的子序列(σ1,σ2),交换两个序列的位置,子序列上需求点个数根据该路径上总需求点个数随机选择,|σ1|+|σ2|不超过该路径上总需求点个数.如图2中b所示.
3) 翻转:随机选择路径上的需求点子序列σ,在原位置进行翻转,|σ|小于该路径上总需求点个数.如图2中c所示.

图2 路径内局部搜索操作示意图Fig.2 Procedure of Intra-route local search
3.2.2 路径间操作
1) 插入:随机选择一条路径r1,并随机选择子序列σ从当前位置删除,随机选择另一条路径r2,将σ插入该路径中的任意位置,|σ|不超过该路径上总需求点个数,若|σ|等于r1上总需求点个数,则r1整条路径被插入其他路径中,删除路径r1.如图3中a所示.
2) 交换:随机选择两条路径r1,r2,分别选取子序列(σ1,σ2),交换两个序列的位置.如图3中b所示.
3) 翻转交换:随机选择两条路径r1,r2,分别选取子序列(σ1,σ2),交换两个序列的位置同时分别将子序列进行翻转.如图3中c所示.

图3 路径间局部搜索操作示意图Fig.3 Procedure of Inter-route local search
|σ1|,|σ2|均不超过路径r1,r2上总需求点个数.
3.2.3 路径操作
随机选择从不同车场出发的两条路径,整条路径进行交换,即交换两条路径的出发车场.
3.2.4 车场操作
若存在未开放的车场,随机选择一个开放车场D1与一个未开放车场D2,交换两个车场,即开放车场D2,将从原开放车场D1出发的所有路径,全部调整为从D2出发,关闭车场D1.
3.3 信息素更新准则
基于一个初始解达到最大变邻域搜索次数后,输出产生的Pareto解集.基于第3.1节中描述的多蚁群构造初始解的方法,以及Pareto解集对多蚁群信息素矩阵的影响,构造新的初始解,本文设计选址、分配和路径选址蚁群信息素更新主要受Pareto解集中总成本最小(各车辆行驶旅程差最大)及各车辆行驶旅程差最小(总成本最大)两个特殊的Pareto解的影响.令该两个Pareto解为X1,X2,任意Pareto解对应的两个目标函数值分别为f1(·),f2(·),各蚁群的信息素更新准则如式(39)-(44),式中ρ,ρ′,ρ′′为各蚁群信息素挥发系数,nk为分配给车场的需求点数量,tL(·)为对应解的总车辆行驶路径长.设选址、分配和路径选址蚁群初始信息素水平为1/fk、极小的数和1/dij,
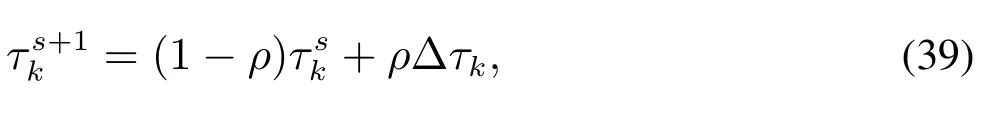
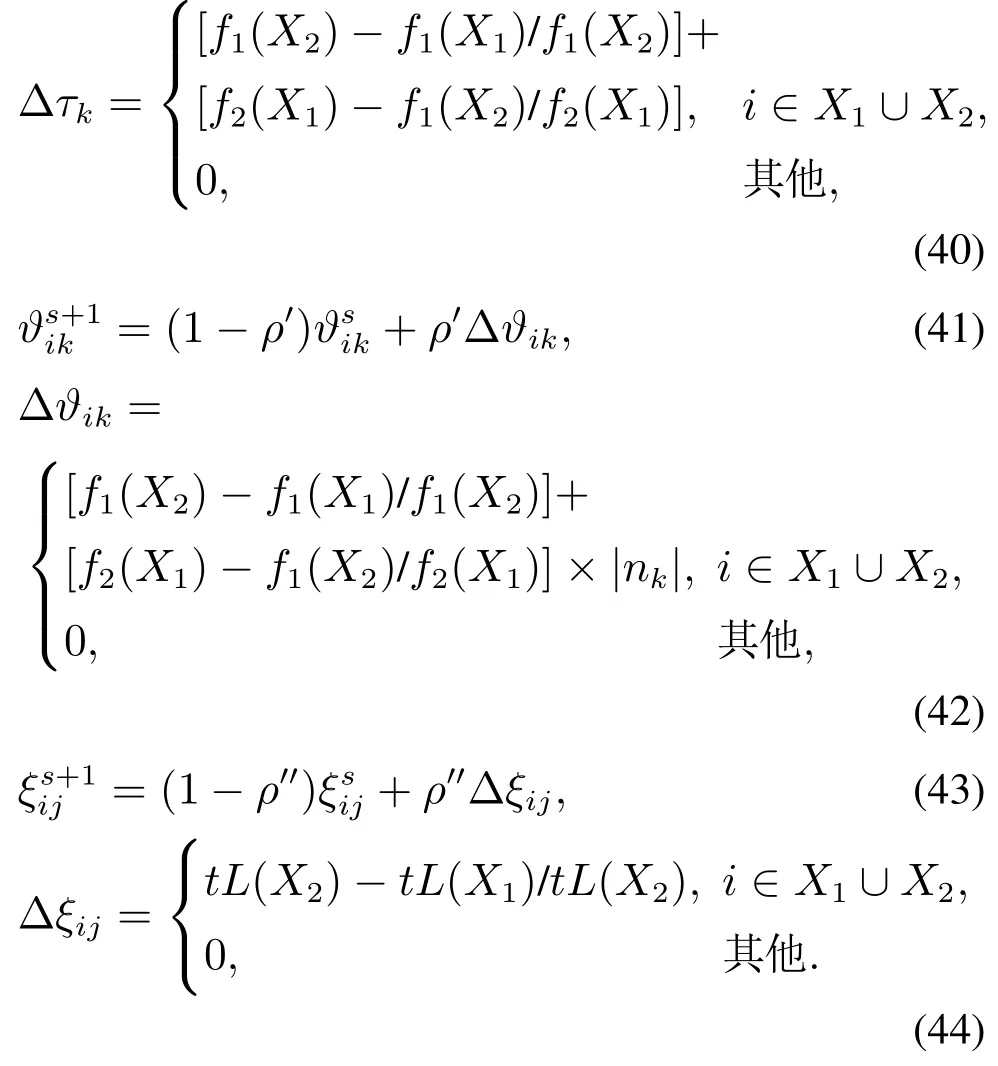
4 算例求解与结果分析
根据以往文献,对蚁群算法中的参数范围进行经验性设置:信息素挥发系数ρ,ρ′,ρ′′ ∈[0.2,0.8],启发式因子α ∈[2,5],β,β′ ∈[0,5],γ,γ′ ∈[0,5],随机因子q0,∈[0.2,0.8].初次分配结束后,对车场容量进行检查,若容量超出对需求点的分配进行调整以确定是否需要额外开放一个车场,分配调整的最大次数nA-max∈[0.5,1,1.52]×|NC|.MSVNS中起点数nMS∈[0.5,1,1.52]×|N|,每一次VNS允许连续产生可行且为支配解的最大次数nF-max∈[0.5,1,1.52]×|N|,允许连续产生不可行解的最大次数为nINF-maxnF-max.基于以上参数范围,从本文采用的Karaoglan等[13]中随机选择4组不同规模的算例进行多组参数组合试验,获得最佳解的参数组合为:ρ,ρ′,ρ′′0.2,0.2,0.2,α2,β,β′3,3,γ,γ′1,2,q0,0.7,0.7,0.8,nA-max|NC|,nMS|N|,nF-max2×|N|.
4.1 算例求解结果
Karaoglan等[13]根据两种不同的需求拆分策略(demand separate strategy,DSS)基于两组LRP算例构造了4组测试算例:BAM,BSN,PAM,PSN,分别简称B,P系列,应用文献[13]中的算例,并设置最大行驶里程为一个较大的常数.运用MATLAB(R2014b)编写代码,在Windows 7操作系统,处理器为Intel(R)Core(TM)i5-4460(3.20 Ghz),8 GB内存的个人电脑上运行程序,每组算例运行10次,不同次运行产生的Pareto解存在相互支配,因此综合10次运行结果得到最优Pareto前沿.基于综合后的最优Pareto前沿,决策者可根据实际偏好进行决策.
4.1.1 边界Pareto解分析
图4(a)(b)分别为BAM,PAM系列中随机算例的所有解集,最优Pareto前沿如菱形所示.图4(a)中不同解的最大行驶里程差波动较大,即不同的选址-路径决策会导致不同车辆的工作量相差较大,而图4(b)中不同决策下车辆的工作负荷相对平均.设近似Pareto解集中100%偏向最小化总成本时对应的两个目标函数值分别为与;100%偏向最小化车辆间最大行驶里程差时为与则

图4 不同系列随机两算例10次运行近似Pareto解集Fig.4 Pareto solutions of 10 runs for 2 random instances from different series
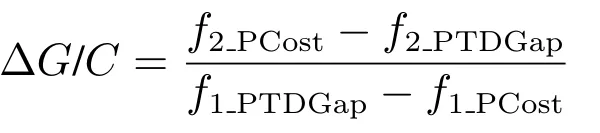
反映了车辆间最大行驶里程差随成本变化的最大波动率.
表1-2列出各算例的ΔG/C值,B系列算例车辆间最大行驶里程差随成本变化的最大波动率最大值分别达178.24,235.34,平均值为58.59,86.5,表明B系列算例不同Pareto解对应的选址-车辆路径方案,在总成本变化不大时车辆间工作量相差较大,体现出决策时考虑车辆间工作量平衡目标的重要性.而表2中P系列算例的ΔG/C值较小,平均值分别为4.48,14.39,即:在不同决策下,各车辆间工作量均相对平均.
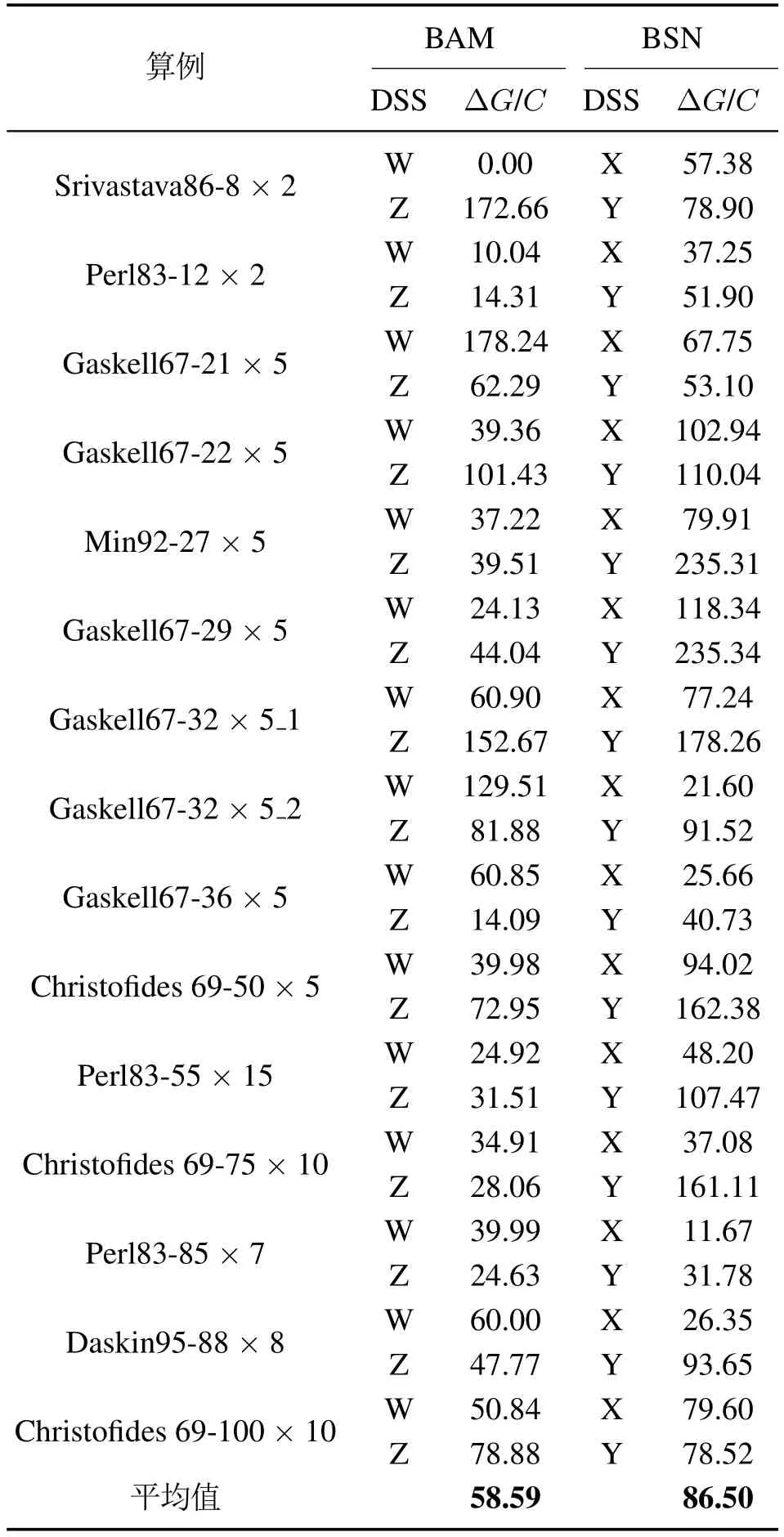
表1 B系列算例边界Pareto解Table 1 Pareto with extreme OFVs for instances sets B
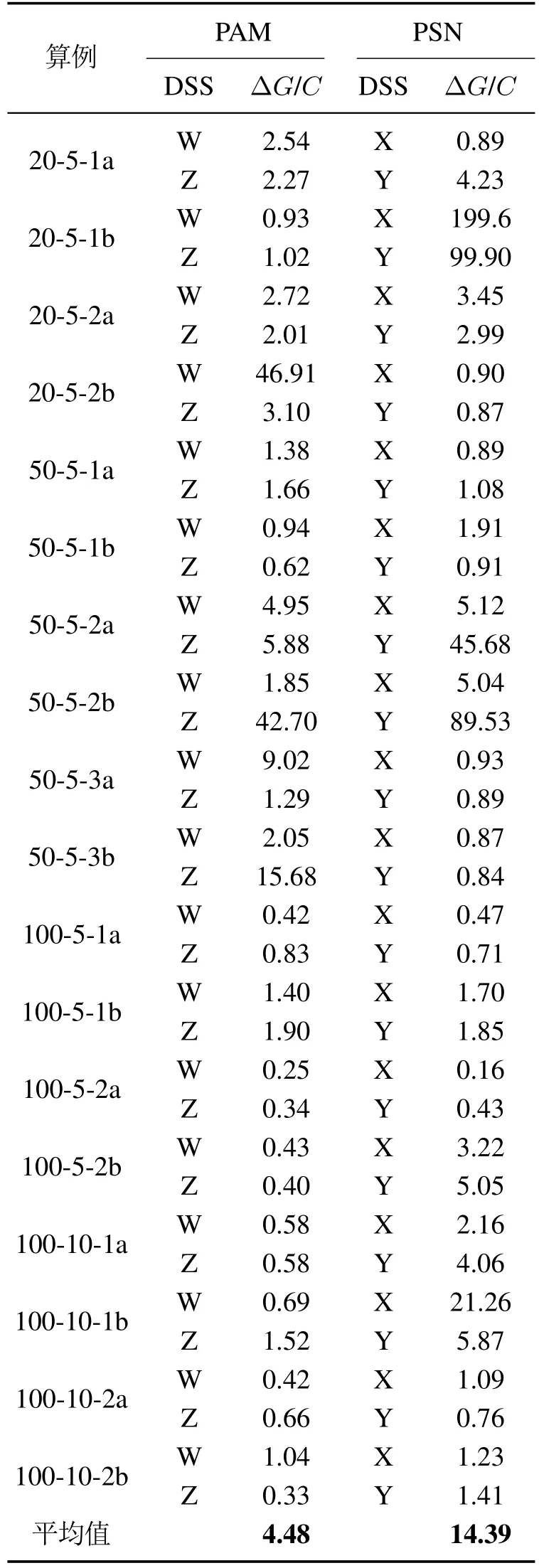
表2 P系列算例边界Pareto解Table 2 Pareto with extreme OFVs for instances sets P
4.1.2 邻域结构性能分析
为了分析四类邻域结构对算法性能的影响,随机选取不同规模的算例,逐一删除四类邻域中的某一类邻域进行测试,获得成本最小的解,如表3所示,其中Gap%表示删除邻域后获得的解与使用全四类邻域的解的偏差,如第4列:
由于算法包含多蚁群、多起点和变邻域搜索3种机制,在3种机制的组合下算法达到较好的性能,而非仅由邻域结构确定;另外,对于不同的算例,某一种邻域操作产生的多样化具有较大的随机性,即某一种邻域结构操作对某一算例可能产生更优的解、同时也未可能产生更优的解,这解释了表3中删除单一邻域结构后对解的影响不甚明显的原因.

表3 邻域结构性能分析Table 3 Performance analysis of neighborhoods
4.1.3 算法性能分析
本文以100%偏向总成本最小函数选取近似Pareto解集中成本最小的解与文献中以最小化总成本为目标求得的解进行对比,提取10次运行求得解集中成本最小的解,分别以最优解和平均解与上界进行比较,得到最小偏差(Gap%min)和平均偏差(Gap%Avg).
B系列算例的解与Karaoglan等[11]获得的上界、B&C算法求得的解、以及模因算法(MA)[16]进行对比,见表4-5,结果显示本文提出的MSVNS可在极短的时间内(平均分别为4.3 s,6.12 s)求解BAM,BSN系列所有算例包含成本近似最优的Pareto解,与上界相比最优解的平均偏差分别为17.57%,17.39%,平均解的平均偏差为17.94%,17.78%,最优解与平均解相差小于0.5%表明了算法的稳定性.尽管整体上解与上界的偏差相较于B&C有一定的差距,但在求解速度上有明显优势,并且部分算例(Perl83-55×15及Perl83-85×7)的解比B&C更优.
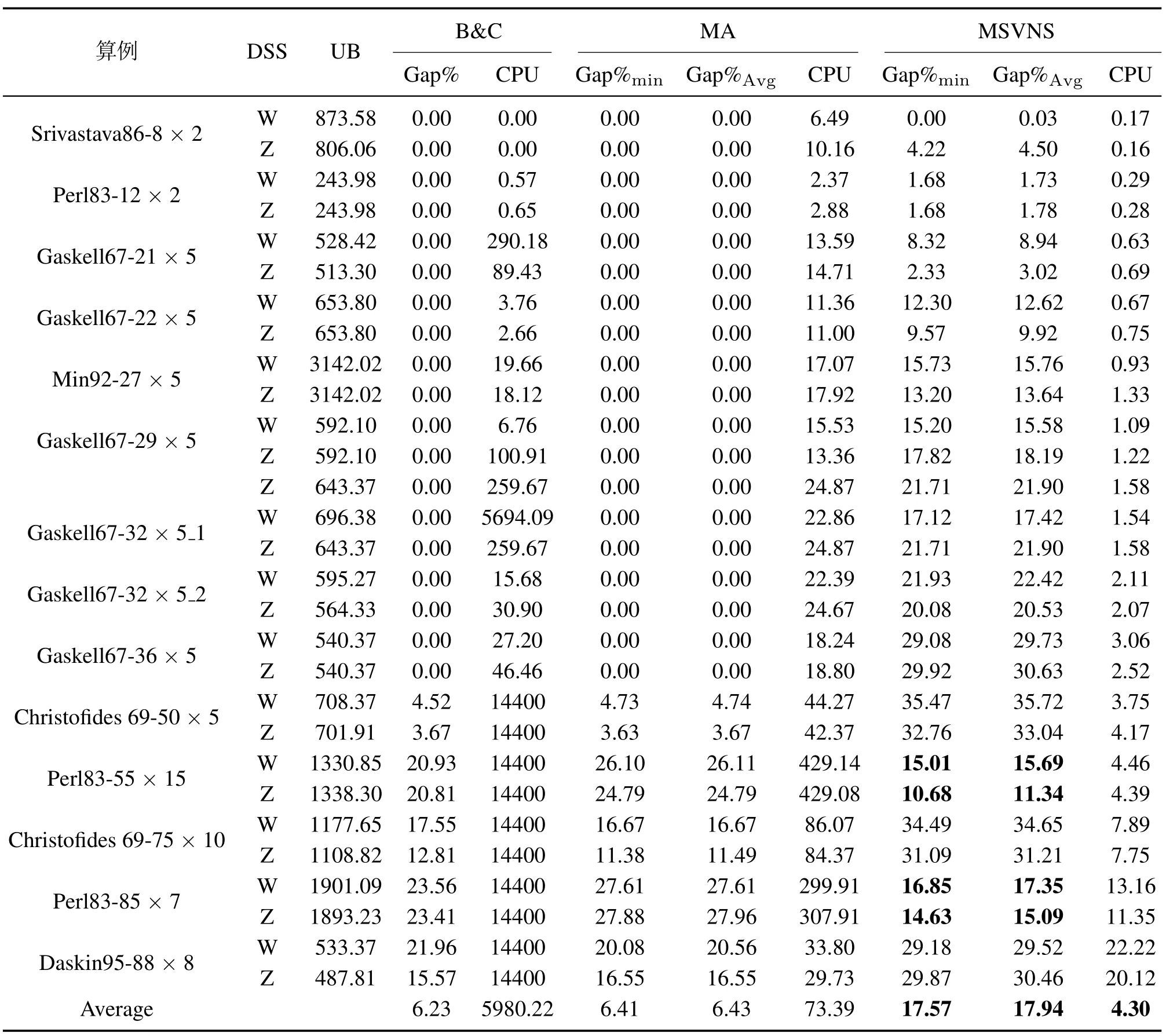
表4 BAM算例MSVNS算法与B&C结果比较Table 4 Results comparison by MSVNS against B&C for BAM instances

表5 BSN算例MSVNS算法与B&C结果比较Table 5 Results comparison by MSVNS against B&C for BSN instances
P系列算例的解与文献[11]上界及B&C获得的解、以及混合遗传算法(hybrid genetic algorithm,HGA)[14]求得的解进行对比,如表6-7,结果表明MSVNS对P系列算例极好的适应性,72个算例中共46个算例获得了比上界更好的解,最好解的平均偏差分别为-1.7,-2.08,平均解的平均偏差分别为-1.59,-1.92,表明算法稳定性,同时说明本文提出的MSVNS求得的平均解的结果优于文献中其他的算法,且求解时间同样具有明显优势.

表6 PAM算例MSVNS算法与文献中已有结果比较Table 6 Results comparison by MSVNS against existing results in literature for PAM instances

表7 PSN算例MSVNS算法与文献中已有结果比较Table 7 Results comparison by MSVNS against existing results in literature for PSN instances
为进一步比较MSVNS求解性能,表8从获得新最优解的数量及平均求解时间与文献[15]中两种模拟退火(simulated annealing,SA1,SA2)及多起点模拟退火算法(multi-start SA,MSA)进行比较.对比P系列不同规模算例的求解结果,MSVNS 仅在50×5规模算例上获得的新最优解略少于SA,MSA,在其他规模算例上均获得了更多最优解,解的精度和平均求解时间均体现出MSVNS求解性能更优.

表8 不同方法获得新最优解的数量及平均求解时间比较Table 8 Number of new best solutions obtained and computational time required by each approach
5 结论
本文考虑车辆容量和最大行驶里程限制,构建了最小化总成本和最小化不同车辆行驶距离最大差以平衡各车辆的工作负荷的双目标LRPSPD模型.提出一种多起点变邻域搜索算法(MSVNS)进行求解,首先基于多蚁群算法构建初始解,基于初始解设计四类邻域结构进行随机变邻域多目标搜索,根据所得Pareto邻域解更新信息素,而后产生新的初始解作为变邻域搜索起点.本文用MSVNS算法求解文献中的算例,解得Pareto前沿的分布情况说明了考虑最小化路径间最大长度差目标的重要意义.与其他求解LRPSPD方法求解结果的比较表明了算法在求解速度上的绝对优势;尤其对于P系列算例,MSVNS在求解精度和求解时间均表现出更优性能,说明MSVNS算法可求得权衡各目标的Pareto解,并使得最小总成本目标近似最优.
文中算法对B系列与P系列求解结果精度差异较大,一方面,算法对于不同算例的普适性需进一步提高,另一方面,不同系列算例与不同算法匹配规律有待进一步分析研究.采用容量较小的车辆并派遣其访问偏远节点,对于平衡车辆的行驶距离,充分利用车辆的装载空间有重要的意义,因此多车型的LRPSPD为未来研究的重要方向之一.基于现实物流情形,同时考虑如时间窗约束、随机行驶时间等其他因素的LRPSPD将是非常值得研究的领域.

