强风环境中下行式移动模架的抗风性能

董 锐，梁斯宇，左文华，翁祥颖，刘 俊

(1.福州大学 土木工程学院，福州 350108；2. 福建工程学院 土木工程学院，福州 350118；3.上海理工大学 环境与建筑学院，上海 200093；4.福建省土木建筑学会，福州350001)

移动模架施工法具有不影响桥下交通、梁体浇筑质量高、省工省料、建造速度快、作业安全等优点[1]，尤其适用于峡谷、滩涂、河流等地面状况较复杂的中小跨度高墩桥梁的现浇施工。目前已广泛应用于广州珠江黄埔大桥、涪江大桥、苏通大桥引桥等大量桥梁建设中。该施工法中的核心设备为移动模架造桥机，简称移动模架(movable scaffolding system，简称MSS)，通常采用钢结构制作，是一种自带模板可在桥跨间自行移位，用于支撑和浇筑混凝土梁体的大型制梁支撑体系[2]，其常用跨径为30～60 m，待制主梁的断面形式主要有箱形、T形和槽形3种。根据钢主梁与待制主梁相对位置的不同，移动模架可以分为上行式、下行式和平行式3种，其中上行式和下行式是最主要的两种类型。

移动模架作为公路和铁路桥梁建设中的一种常用高处作业施工设备，中国多部标准[2-9]对其在强风环境中的安全性作出了具体规定：当风力大于6级时，作为高处作业设备的移动模架应停止施工。随着移动模架工作高度和跨越长度不断增长，结构的风敏感性也逐渐增强，其在强风环境中的抗风安全性问题日益突出。当工程场地位于东南沿海强风区域时，移动模架施工面临着6级及以上强风占比较高而导致的工期延长和台风环境中的抗风安全性两大问题。在保证结构安全的前提下，为有效拓展强风区域移动模架的有效作业时间，有必要对其抗风性能展开系统研究。

目前，对移动模架的国内外研究主要集中在设计理论、加工制造、维护再利用、空间受力与裂缝控制、静力安全性、经济性等方面，对于其抗风性能的研究相对较少[10-17]。文献[10]针对现行欧洲风荷载规范缺少移动模架结构抗风设计方法的现状，以土耳其安卡拉某一设计中的90 m超大跨移动模架为研究对象，对结构不同阶段设计风速的选择进行了分析，并提出移动模架的实际施工需要同时考虑设计风速限值、现场的实际风速预报和设计者的决策3个因素，同时建议通过概率方法对移动模架因风作用发生事故的概率进行计算。文献[11]给出了移动模架不同阶段的设计风速建议值，其中运行状态时的平均风速设计值为11.11 m/s(40 km/h)，阵风风速设计值为16.67 m/s(60 km/h)，锁定状态时的风速设计值为38.89～47.22 m/s(140～170 km/h)，与《铁路移动模架制梁施工技术指南》[2]中的建议值大致相当。文献[12]给出了移动模架最大变形建议值为主梁跨度的1/400。文献[13]以Eurocode 3、AISC、NS 3472E、AASHTO和BS 5950等相关标准为依据，对韩国釜山-永道大桥采用的上行式移动模架的设计和施工过程的风致响应进行了分析。文献[15]以广州珠江黄埔大桥采用的主跨62.5 m的上行式移动模架为研究对象，在均匀流场中进行了气弹模型风洞试验，并对结构最不利状态时的颤振、驰振、涡振和抖振性能进行测试和分析，但该文献采用的均匀流场气弹模型风洞试验，仅能够对尾流紊流引起的抖振进行模拟，不能反应来流紊流的影响，存在明显不足。文献[16]基于《铁路桥涵设计基本规范》(TB 10002.1—2005)中的等效风荷载计算方法，采用有限单元法对武汉天兴洲公铁两用大桥北引桥所用的40 m跨平行式移动模架进行了位移、强度和稳定性分析，结果表明，规范给出的横风向风荷载的影响很小，计算中可以忽略。文献[17]针对平潭海峡的强风特性，提出了一种理论上的移动模架结构改造方式，但并未开展相关风洞试验研究，移动模架改造后的抗风性能值得商榷。

针对强风区域移动模架抗风研究的不足，本文以东南沿海地区某高架桥施工采用的具有代表性的MSS50下行式移动模架为研究对象，采用理论分析、数值计算和风洞试验相结合的方法对其在强风环境中的抗风性能进行了系统研究，主要包括结构动力特性精细化分析、移动模架气动弹性模型风洞试验和基于风洞试验的结构抖振响应分析。相关结论可为中国东南沿海强风区域移动模架抗风安全性评估理论的完善提供参考和技术支撑。

1 结构动力特性分析

1.1 工程背景

本文中的下行式移动模架为平潭海峡公铁两用大桥引桥部分现浇混凝土箱梁所采用的施工设备，工程场地周边为低矮建筑物稀少的乡村地区，地形为平缓丘陵，根据《公路桥梁抗风设计规范》(JTG/T 3360-01—2018)[18](以下简称桥梁抗风规范)，场地类别偏安全地取为B类场地，相应的地表粗糙度系数α0=0.16，地表粗糙高度为z0=0.05。施工中使用的移动模架造桥机为主跨50 m的下行式移动模架(以下简称MSS50)，采用全钢结构制作，结构受力主体由钢主梁与横撑、前导梁(又称鼻梁)、模板系统、前/后横梁和辅助支腿五大部分组成。钢主梁总长63.2 m，截面宽2.2 m，高3.4 m，钢主梁间距在合模工况下为11.2 m，开模工况下为19.6 m，主梁离地面的基准高度为43.61 m；前导梁为移动模架过孔时的辅助设备，采用格构式钢桁架结构，总长41.7 m。外模板为浇筑混凝土箱梁的支撑系统，由主板、加劲肋板和支撑架组成，通过支撑杆与主梁连接成整体。移动模架立面布置和横截面分别如图1和图2所示。

1.2 设计基准风速

根据桥梁抗风规范[18]计算得到的桥址处不同重现期的设计基准风速和施工阶段的设计风速见表1。由表1可知，如果将移动模架视为固定装置并按照规范进行抗风验算，则10 a重现期时的设计基准风速为52.89 m/s；如果按照主桥施工阶段进行抗风验算，则主桥100 a重现期对应的施工阶段的设计风速为49.59 m/s，均高于14级强台风的风速(41.5～46.1 m/s)，达到15～16级强台风的范围。鉴于侵袭中国东南沿海地区的台风到达陆地时基本上都在14级以内，如果移动模架按照49.59 m/s的设计基准风速进行抗风设计会造成很大的浪费。因此，分别取8级风(风速17.2～20.7 m/s)和14级风(风速为41.5～46.1 m/s)对应的风速上限Ud1=20.7 m/s和Ud2=46.1 m/s作为移动模架正常使用极限状态和承载能力极限状态时的检验风速，以0～20.7 m作为涡振检验风速范围。

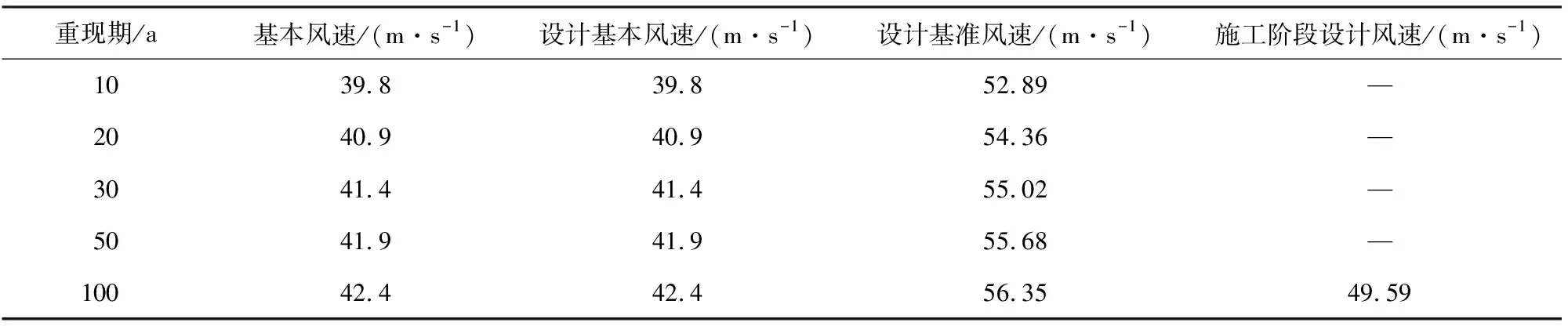
表1 桥址处不同重现期的基本风速和设计基准速

1.3 颤振检验风速

根据桥梁抗风规范[18]的规定，颤振检验风速[Uf]可以按下式计算：

[Uf]=γfγtγαUd

(1)

式中:γf=1.15为颤振稳定分项系数，γt=1.36为风速脉动空间影响分项系数，γα=1.0为攻角效应分项系数。由此得到颤振检验风速为72.1 m/s。

1.4 动力特性分析

本文采用ANSYS对MSS50下行式移动模架进行有限元模拟，其中钢主梁、外模板、加劲肋采用壳单元SHELL 181模拟，横撑、前导梁、辅助支腿、混凝土桥墩采用空间梁单元BEAM 188模拟,钢筋与支撑杆采用空间杆单元LINK 180模拟。结构有限元模型如图3所示，各部分材料特性汇总见表2。

对MSS50合模和开模最不利工况时的有限元模型进行模态分析，分别获得结构的主要振型和频率见表3。由表3可知，移动模架合模工况(工况I)时的一阶竖弯、一阶侧弯和一阶扭转频率分别为3.394 1、2.119 5、4.123 8 Hz，主体结构的一阶振型出现在侧弯方向，为该工况时的相对薄弱方向。合模工况时，移动模架两幅主梁通过17道桁式横撑紧密联合，且外模板紧密相接，结构的整体刚度相对较大，主体结构振型特征与连续梁桥类似；开模工况(工况II)时，移动模架一阶竖弯、一阶侧弯、一阶扭转频率分别为3.599 1、3.262 1、1.809 5 Hz。开模工况时，由于17道桁式横撑分离，移动模架的扭转刚度显著降低，约为合模工况时的44%，是该工况时的薄弱方向。

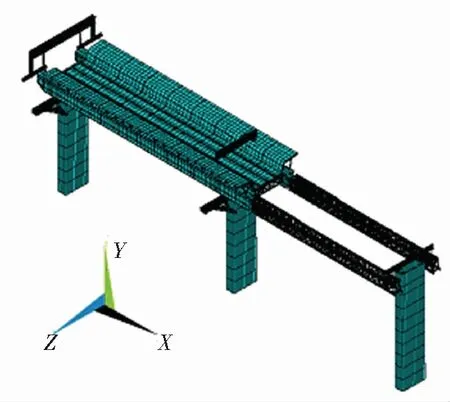
(a)合模工况

(b)开模工况

表2 有限元模型中所用材料参数

表3 MSS50下行式移动模架有限元模型主要振型与频率

2 气动弹性模型风洞试验

为明确MSS50下行式移动模架在强风环境中的抗风性能，本文采用气弹模型风洞试验对结构在不同流场、不同风速时的颤振、涡激振动和抖振性能进行了检验。风洞试验在上海理工大学环境与建筑学院大气边界层风洞中完成，其中气弹模型颤振和涡振稳定性在均匀流场中完成，抖振性能在均匀紊流场中完成。

2.1 试验设计

为了确保气弹模型风洞试验能够真实地反映实际结构在风环境中的响应，试验需要模拟原结构的几何尺寸、气动弹性特性和桥址处的风场特性，以满足几何相似性、气弹相似性和流场相似性3个条件[19]。

2.1.1 模型设计

MSS50下行式移动模架气弹模由钢芯梁、箱型主梁外衣、外模板、鼻梁、桥墩和牛腿组成，根据相似原理，模型按照桥梁抗风规范[18]C.5条表C.5.1进行设计，其中试验风速比取1∶10，仅在开模扭转工况下试验风速比取1∶12.8；MSS50移动模架气弹模型主要几何尺度的相似比取1∶32，则气弹模型单位长度质量与单位长度质量惯性矩的相似比分别为1∶322和1∶324，合模与开模工况下一阶竖弯频率相似比为32∶10，合模与开模工况下一阶扭转频率相似比分别为32∶10和32∶12.8。根据以上相似比得到的MSS50移动模架气弹模型几何尺度、单位长度质量与单位长度质量惯性矩以及一阶竖弯频率与一阶扭转频率的计算值以及实测值分别见表4、表5和表6。

表4 MSS50移动模架气弹模型几何尺度

表5 MSS50移动模架气弹模型单位长度质量与单位长度质量惯性矩

表6 MSS50移动模架气弹模型一阶竖弯和扭转频率

2.1.2 风场模拟与试验工况

本文中的MSS50下行式移动模架属于水平线状结构，且混凝土桥墩刚度较大，可视为固接，故风洞试验中不模拟平均风剖面和湍流度随高度的变化，紊流场采用顺风向紊流强度Iu=15%的均匀紊流场。均匀紊流场通过布置格栅获得，采用热线风速仪进行测试，分别获得3、6、8 m/s风速时的顺风向紊流度在14.3%～16.5%之间的流场，满足试验要求。针对不同的研究目的，试验分别在均匀流场和紊流场中进行，试验工况汇总见表7。

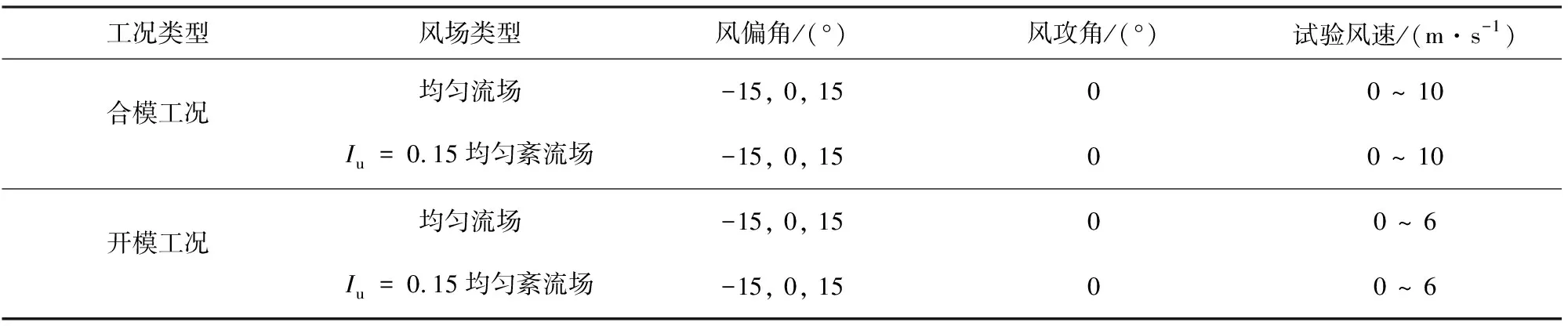
表7 MSS50气弹模型风洞试验工况

2.1.3 测点布置

MSS50气弹模型风洞试验采用的测量设备为Panasonic HG-C1100激光位移计(6个)，激光位移计布置在移动模架主梁的跨中和四分点处，测点布置示意、来流风向和风偏角正方向规定如图4所示,气弹模型在风洞中的布置如图5所示。

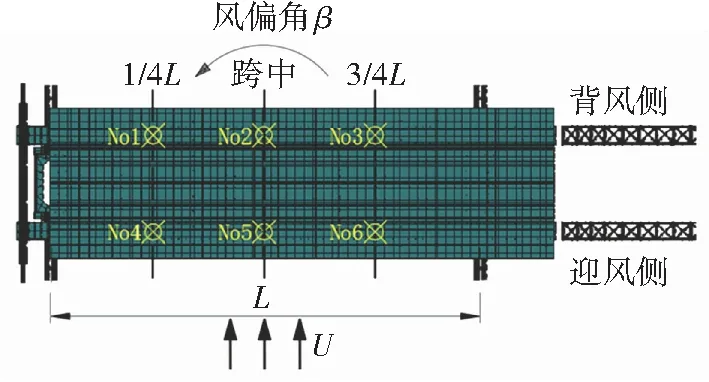
(a)合模工况

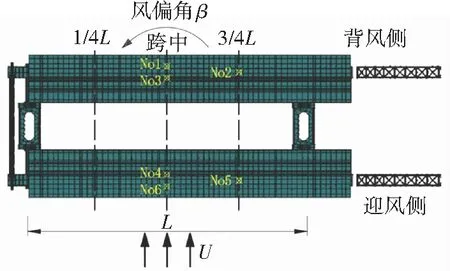
(b) 开模工况

图5 MSS50气弹模型在风洞中的布置

2.2 试验结果

MSS50气弹模型风洞试验通过高精度激光位移计直接获得结构在不同工况、不同风速时的位移响应时程曲线。结构位移响应幅值定义为

(2)

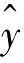
2.2.1 均匀流场中移动模架风振响应

MSS50气弹模型在均匀流场中的风振位移响应随风速变化曲线分别如图6和图7所示。图中各测点风振响应与风速均已转换成实际结构对应的位移响应与风速，各测点的相对位置与方向定义见2.1节，其中扭转角以逆时针转向为正。

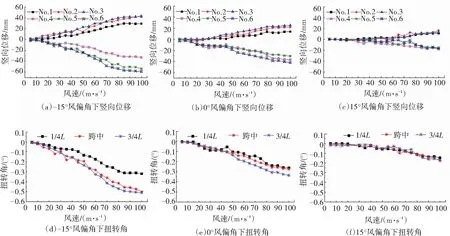
图6 MSS50在均匀流场中的位移响应随风速变化曲线(合模工况)

图7 MSS50在均匀流场中的位移响应随风速变化曲线(开模工况)

从曲线图6中可以看出，在合模工况下，当风力等级在8级(17.2～20.7 m/s)以内时，移动模架的风振幅值增长缓慢，当风力等级达到15级(46.2～50.9 m/s)之后，风振响应幅值才出现较大的增长趋势，但在颤振检验风速(72.1 m/s)内未观测到明显的发散性振动，即其颤振临界风速远大于颤振检验风速；从图7中可以看出，由于开模工况下移动模架迎风侧结构对风的阻挡效应，移动模架背风侧的位移响应幅值远小于迎风侧。当风力等级在8级(17.2～20.7 m/s)以内时，移动模架迎风侧结构的风振幅值增长缓慢，未出现发散性振动，故开模工况下颤振临界风速大于8级风速。图中结构扭转增长幅度最为明显，是控制结构安全与施工精度的最主要因素。观察图6和图7中可以发现试验风速范围内均未发生明显的涡激振动。

2.2.2 紊流场中移动模架风振响应

自然界中的风均为紊流，为评估MSS50的抖振响应，本文进行了顺风向紊流度Iu=15%均匀紊流场的气弹模型风洞试验。MSS50气弹模型在均匀紊流场中的风振位移响应随风速变化曲线分别如图8和图9所示，No.1～No.6的位置标注在图4(a)中。

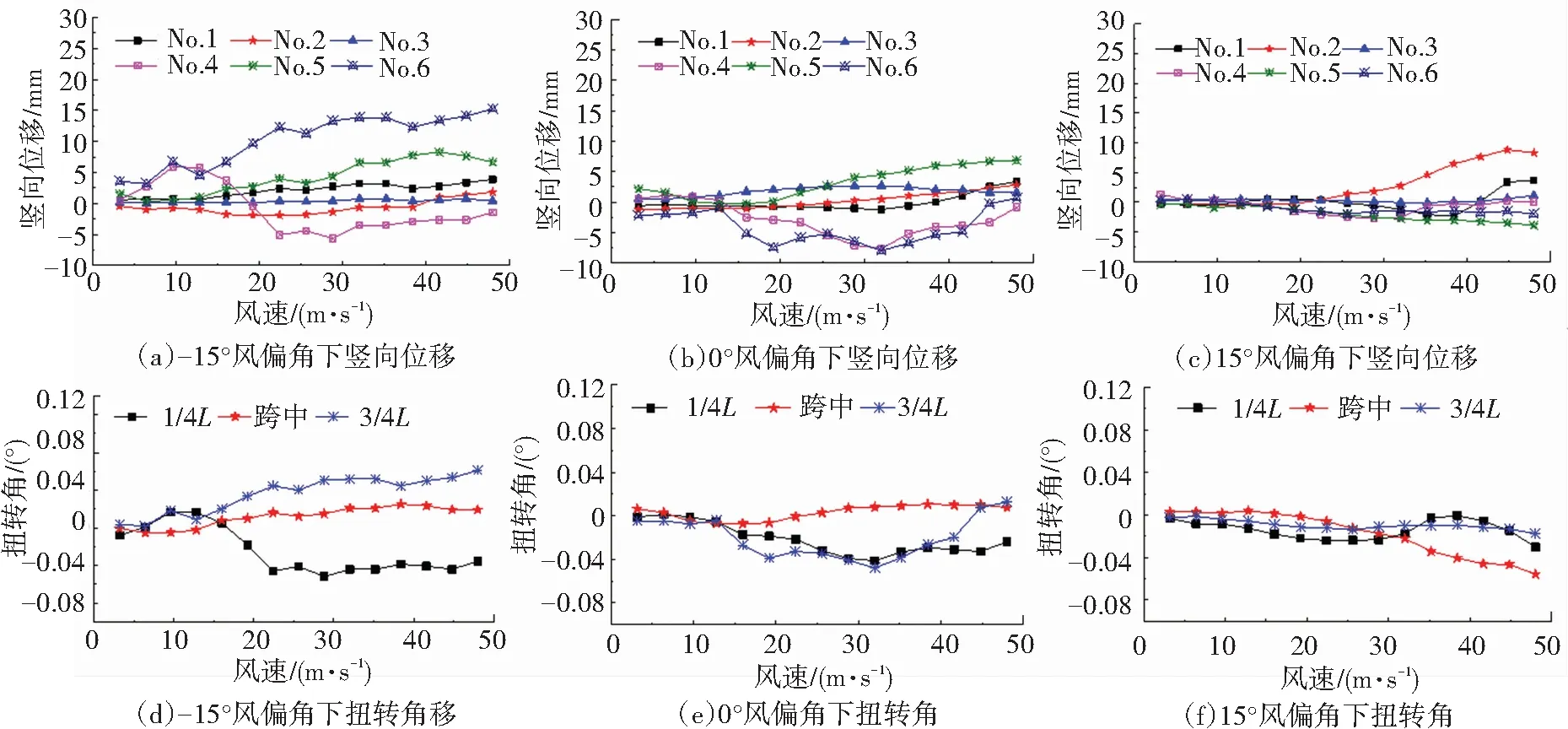
图8 MSS50在均匀紊流场中的位移响应幅值随风速变化曲线(合模工况)

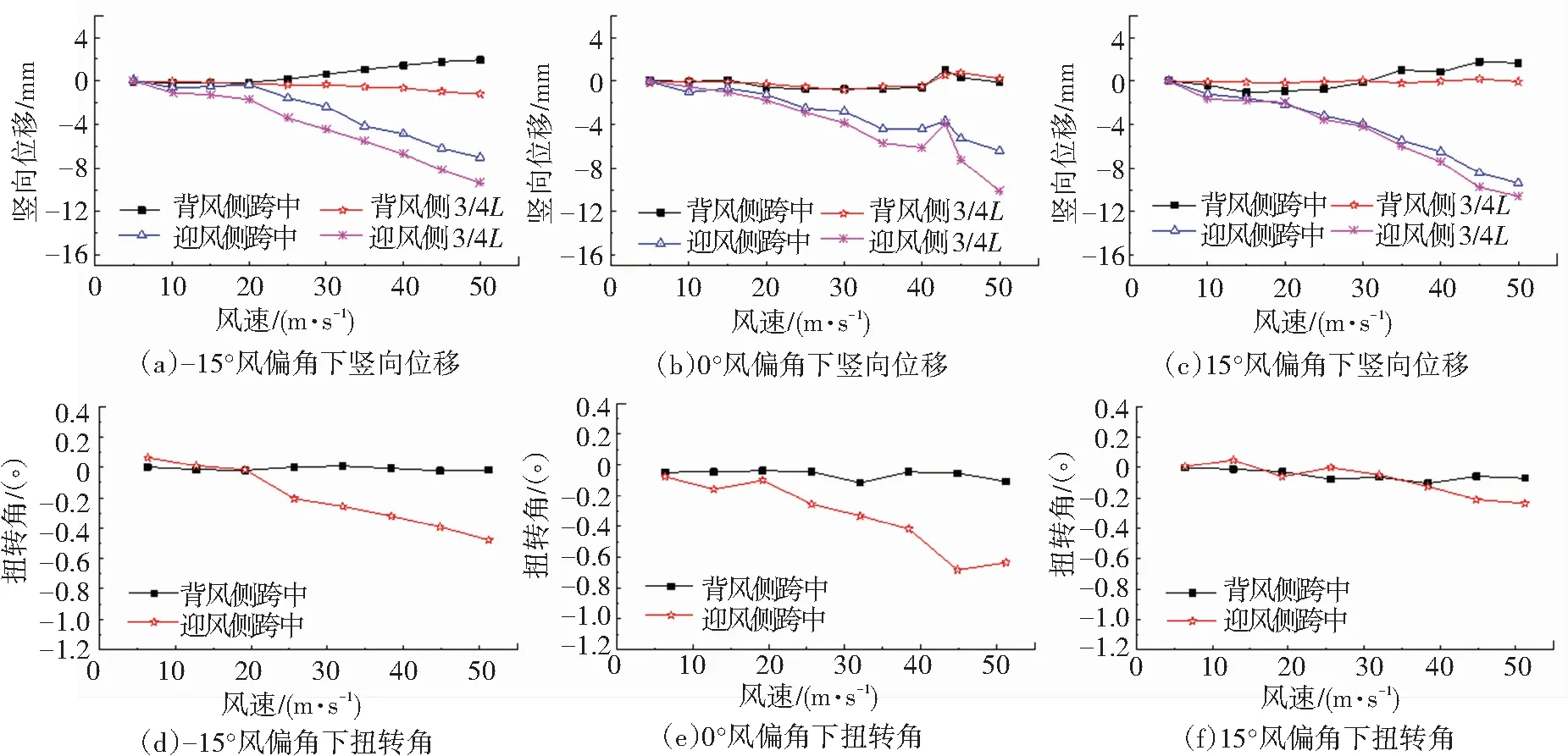
图9 MSS50在均匀紊流场中的位移响应幅值随风速变化曲线(开模工况)

由图8和图9中可以看出，由于脉动风的干扰作用，紊流场中移动模架风振响应-风速曲线更为复杂。图8表明，在合模工况下，当风力等级小于6级(10.8～13.8 m/s)时，移动模架位移响应幅值较小；随着风速的增加，当风力等级在7级(13.9～17.1 m/s)以上时，移动模架扭转变形逐步加大，并逐渐转变为反对称扭转。图9中表明，在开模工况下，当风力等级在8级(17.2～20.7 m/s)以下时，移动模架迎风侧结构的风振响应幅值增长较为平缓，随后增长幅度逐渐增加；当风力等级在8级(17.2～20.7 m/s)以上时，移动模架风振响应幅值增长趋势明显增大，移动模架背风侧结构风振响应幅值远小于迎风侧风振响应幅值。

由于桥梁抗风规范[18]对抖振响应限值并无明确规定，本文根据移动模架施工指南[2]对移动模架抖振振幅进行检验。依据移动模架施工指南第2.2.5条规定，主梁挠度不应大于L/550，其中L=50 m为主梁支撑跨度。主梁开模和合模工况时的特征宽度B分别为6.7 m和13.4 m，根据竖向位移限值可以进一步获得移动模架此时的扭转角限值，规范检验值计算结果及紊流场中的试验结果汇总见表8。

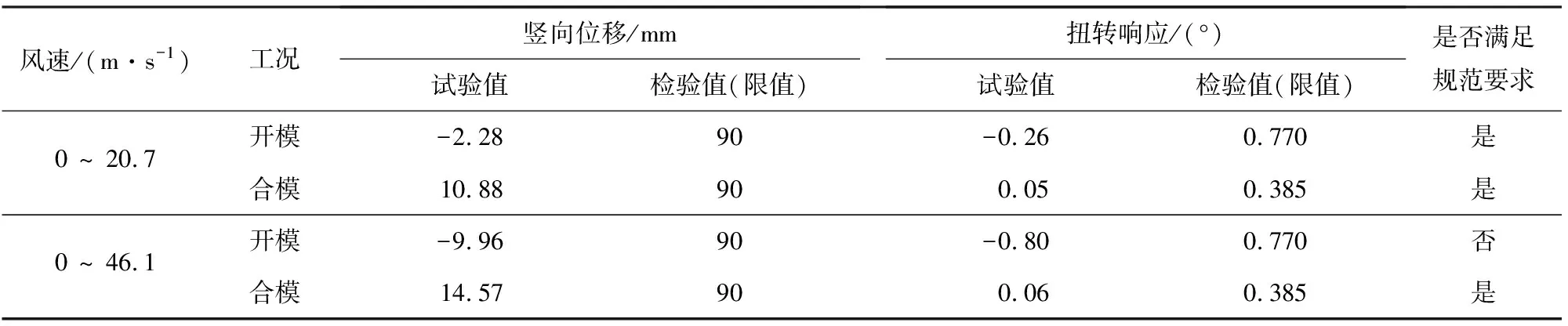
表8 MSS50抖振性能检验结果

由表8可得MSS50下行式移动模架合模工况时，14级风速(46.1 m/s)抖振竖向位移响应幅值为14.57 mm，扭转响应幅值为0.06°，均远低于限值，能抵抗14级风作用；开模工况时，在8级风(20.70 m/s)时抖振竖向位移响应幅值为-2.28 mm，扭转响应幅值为-0.26°，均低于限值，能抵抗8级风作用。在14级风时，扭转响应幅值为-0.8°，略大于限值，偏不安全。

对比开模和合模工况下的风振响应-风速曲线可以看出，由于开、合模两种工况下结构刚度存在不同，合模时结构变形以平动为主，开模时结构变形以扭转为主。对比均匀流场和均匀紊流场中的移动模架风振响应-风速曲线，可以看出紊流场中风振位移响应幅值远小于均匀流场中风振响应幅值，故文献[15]中通过均匀流场中的全桥气弹模型风洞试验结果进行抖振分析的做法存在明显的不妥。

3 基于风洞试验的抖振响应分析

3.1 刚体模型测力风洞试验

为准确获得作用在MSS50上的静风三分力系数，本文采用3D打印技术设计制作了1∶64的刚体模型，并分别进行了均匀流场中开模和合模两种工况时的测力风洞试验，模型在风洞中的布置如图10所示。

MSS50在0°风攻角时各工况的静风三分力系数见表9，限于篇幅，其他角度的静风三分力系数不再给出，参见文献[20]。其中参考特征长度为移动模架投影高度H=7.67 m。

表9 MSS50静风三分力系数及变化率(0°)

3.2 简化等效模型

为便于分析MSS50下行移动模架在脉动风作用下的抖振响应，以1.4节的精细化有限元模型为基础，根据结构质量等效、动力等效和刚度等效[21]的原则建立简化等效模型。其中，质量等效通过计算出全桥中主体结构的等效质量并施加于等效模型的主梁实现；动力等效通过保证原模型与等效模型一阶竖弯和一阶扭转振型频率一致实现。对于等效后的模型，其质量矩阵m，刚度矩阵k和频率矩阵ω存在以下关系：

(3)

在保证等效模型质量与动力特性与原模型一致后，刚度自然保持一致。简化后的MSS50下行式移动模架等效模型如图11所示，简化等效模型与精细化模型主要频率比较见表10。可以发现，结构对应的一阶竖弯和扭转频率相差很小，合模工况下原模型和等效模型一阶竖弯与扭转频率相对误差分别为0.07%和0.065%；开模工况下原模型和等效模型一阶竖弯与扭转频率相对误差分别为0.03%和1.02%，均在3%以内，满足工程计算要求。

(a)合模工况

(b)开模工况

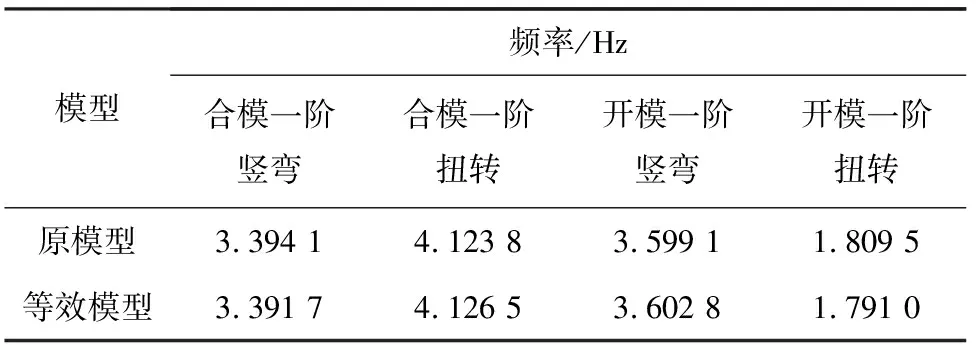
表10 MSS50等效模型动力特性计算表

3.3 等效静阵风荷载法

桥梁抗风规范[18]在考虑风的空间相关性等因素的基础上采用了“等效静阵风”的概念，将作用于结构或构件上具有空间相关性的阵风风速称为等效静阵风风速Ug，计算公式为

Ug=GVUd

(4)

式中:Ud为设计基准风速;Gv为静阵风风速系数，是考虑了紊流强度、脉动风空间相关性、加载长度(高度)和结构离地面(或水面)高度等因素，采用Kaimail水平风谱计算的顺风向风荷载的风速比例系数，使等效阵风中包括了平均风和脉动风两者的综合效应，不同地表类别下的等效静阵风风速GV可参照桥梁抗风规范[18]表5.2.1取值。

获得等效静阵风风速Ug后，作用于主梁单位长度上的三分力可表述为

(5)

(6)

(7)

其中：FH为作用在主梁单位长度上的气动横向力，N/m；FV为气动竖向力，N/m；FM为气动升力矩，N·m/m；ρ为空气密度，可取为ρ=1.25 kg/m3；CH、CV、CM分别为各风攻角下的阻力系数、升力系数和升力矩系数，由MSS50刚体模型测力风洞试验获得；H为结构的特征高度。

本文中移动模架主体结构水平加载长度为58.6 m，施工场地为B类，依据桥梁抗风规范[18]表5.2.1取等效静阵风系数GV=1.33，故可通过式(5)～(7)得到作用在主梁上的等效静阵风荷载，进而通过有限单元法获得结构的抖振响应极值。

3.4 抖振响应频域分析

多模态耦合抖振分析法[22]考虑了结构多阶模态及其耦合效应，是水平线状结构抖振分析中经常使用的一种方法，对于绝大部分结构的抖振计算具有足够的计算精度。本文抖振频域分析中，抖振力采用Davenport准定常抖振力模型。由于移动模架在开模工况时，竖弯刚度远大于扭转刚度，现有的二维节段模型测振风洞试验很难实现，故本文抖振频域计算时未考虑自激力的影响，气动导纳偏安全的取为1。

MSS50抖振响应计算中同时考虑水平和竖向的脉动风作用，相应的水平和竖向脉动风谱分别采用Kaimal谱和Lumley-panofsky修正风谱[23]，如式(8)和式(9)所示：

(8)

(9)

式中：Su(n)为脉动风水平顺风向分量功率谱密度函数，Sw(n)为脉动风竖直分量功率谱密度函数，n和f分别为脉动风频率和折算频率，且f=nZ/U(Z)，u*为风的剪切速度。

水平和竖向脉动风的交叉风谱仅考虑余谱Cuw的作用，计算中采用适合工程应用的经验表达式为

(10)

脉动风的空间相关性采用桥梁抗风规范[18]建议形式：

(11)

式中：下标i和j分别表示脉动风分量(i=u,v,w)和空间相关方向(j=x,y,z)；rij表示空间两点之间的距离；λ表示无量纲衰减因子，取值为7～21，本文取λ=7；f表示折算频率。

考虑结构的前20阶振型，采用CQC组合获得MSS50频域抖振响应极值如图12、13中频域法计算结果所示。

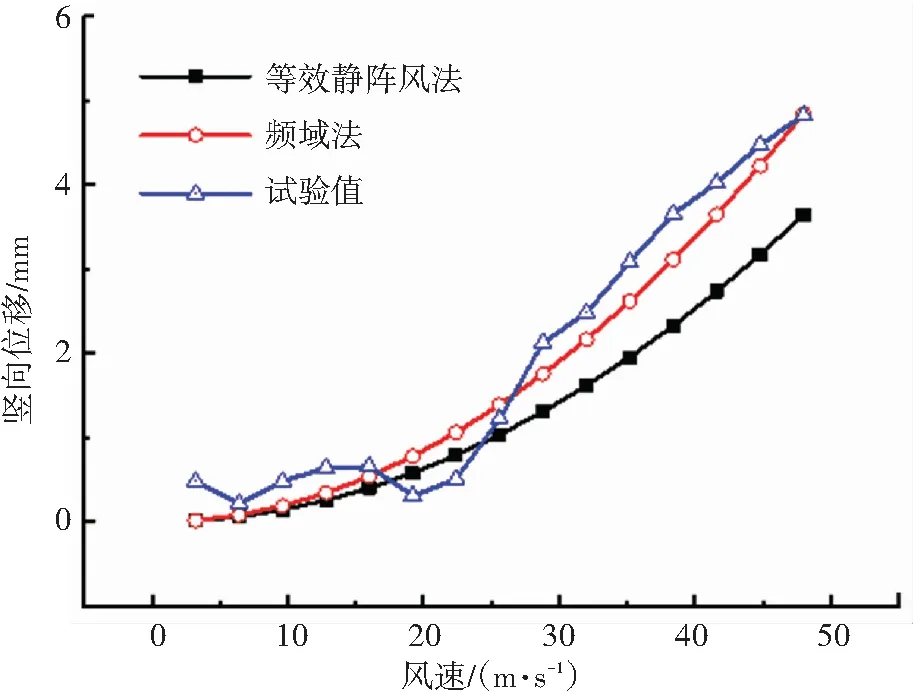
(a)竖向位移

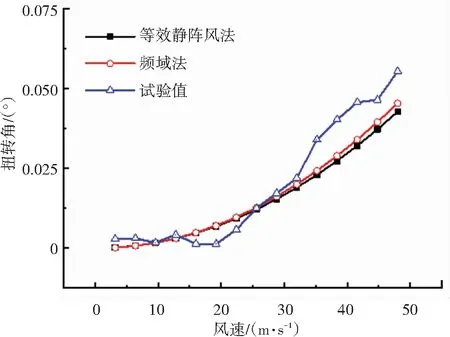
(b)扭转角

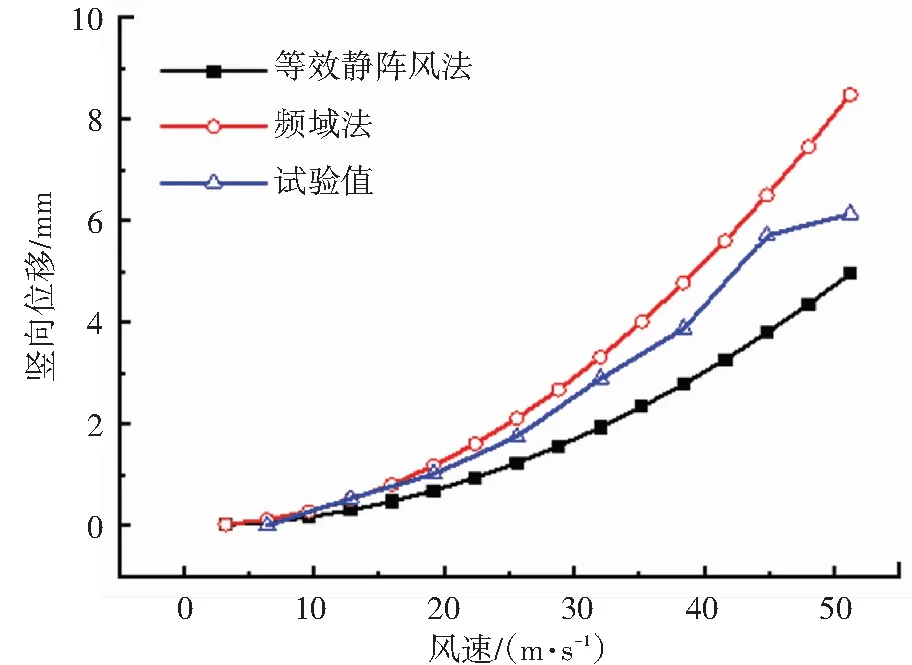
(a)竖向位移

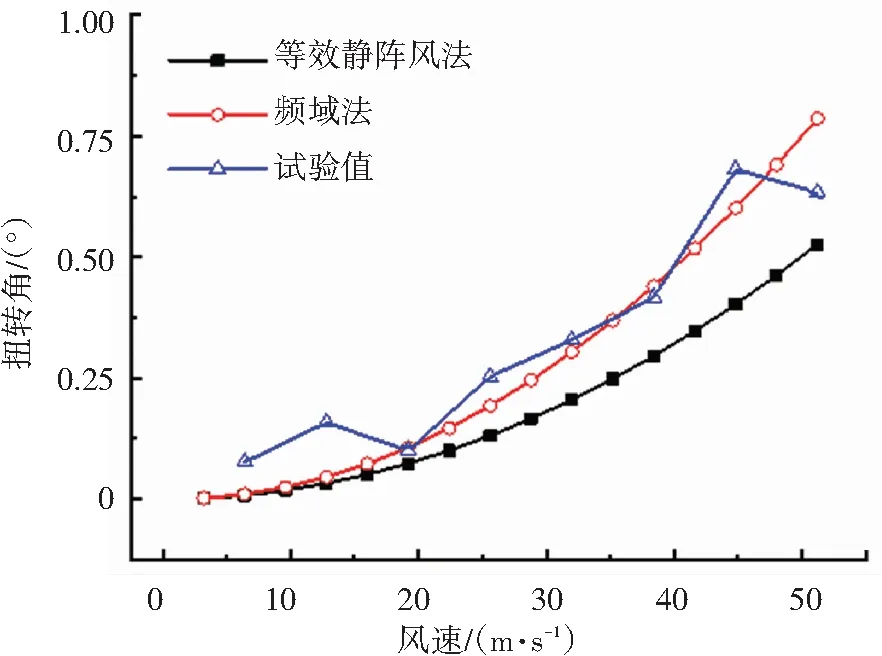
(b)扭转角

3.5 基于风洞试验的抖振响应评估

以MSS50气弹模型风洞试验为基准，将风洞试验结果与等效静阵风荷载法(以下简称规范法)、多模态抖振频域分析法(以下简称频域法)的计算结果进行比较。其中，试验值与计算值均取最不利位置处的抖振响应极值。图14、15所分别给出了规范法与频域法在48 m/s风速时MSS50的抖振响应极值分布，由于其他风速时结构的抖振响应极值分布规律相同，限于篇幅不再给出。从图中可以看出，除开模工况时的扭转角抖振响应最不利位置出现在MSS50最大悬臂端部，其余工况时均发生MSS50钢主梁跨中位置。为便于与气弹模型风洞试验对应，本文所有的抖振响应安全性评估以主梁跨中位置处的数值为比较对象。为避免重复，风洞试验结果与数值计算结果的比较汇总于图12和图13中。

图14 MSS50规范法抖振响应计算值分布图(0°风攻角)

(a)合模工况-竖向位移 (b)合模工况-扭转角 (c)开模工况-竖向位移 (d)开模工况-扭转角

从图12可以看出，合模工况时，对于竖向位移响应，规范法、频域法的抖振响应计算值在风速小于24.4 m/s(9级)时，均与风洞试验结果吻合良好，随着风速增大，频域法计算值增大的速率要大于规范法；在46.1 m/s的风速之内，频域法计算值与风洞试验结果吻合良好；在24.4～46.1 m/s的风速之间，规范法计算值要小于风洞实验结果。对于扭转响应极值，规范法和频域法的计算值吻合良好，且在28.4～46.1 m/s的风速之间均小于风洞试验结果。从图13可以看出，开模工况时，对于竖向位移，规范法和频域法的计算值与风洞试验结果的变化趋势相同，但频域法计算值随风速增大而增大的速率要大于频域法。在46.1 m/s的风速之内，频域法获得竖向位移计算值与风洞试验结果吻合较好，且略偏安全。对于扭转响应极值，在46.1 m/s的风速之内，频域法计算值与风洞试验结果吻合良好，且均大于规范法计算值。

进一步对规范法和频域法的计算精度进行分析，获得计算值与试验值的判定系数见表11，可以发现，如果采用频域法对MSS50抖振响应进行模拟，判定系数基本都在0.9左右，表明两者吻合良好，可以用于实际工程。与频域法相比较，规范法的拟合精度相对较低，除开模工况扭转角外，判定系数均在0.75左右。开模工况下，扭转角规范法计算值与试验值的判定系数仅为0.468，误差相对较大，但是考虑到两者之间的绝对误差数值很小，均值为0.12°，且规范法具有简单直观的特点，也基本能够满足工程建设的需要。

表11 MSS50抖振响应试验值与计算值的判定系数

4 结 论

本文选取东南沿海具有代表性的50 m跨下行式移动模架MSS50为研究对象，采用风洞试验、数值计算和理论分析相结合的方式对其抗风性能进行了较系统的研究，主要结论如下：

1)强风环境中，合模和开模工况下影响结构安全及施工精度的主要控制因素分别是结构竖向位移和扭转角，工程师应根据移动模架不同的工作条件，选择合适的抗风性能指标。

2)气弹模型风洞试验表明，50 m跨下行式移动模架在设计风速范围内不会发生颤振和明显的涡激振动现象。

3)合模工况时，MSS50主体结构能够满足8级强风的作业要求，且能够抵抗14级风作用；开模工况时，在措施得当的情况下主体结构能够满足8级强风的作业要求，但需最大限度缩短开模行走时间，尽可能避免在强风期间行走。

4)移动模架抖振响应计算时，频域法和规范法均能够满足工程建设的需要，但频域法的计算精度要明显高于规范法。推荐优先采用频域法进行移动模架抖振响应的计算。