直升机悬停救助模拟器工作空间分析
王盛业,王海涛,熊伟,关广丰
(大连海事大学船舶与海洋工程学院,辽宁大连 116026)
0 前言
自从1965年STEWART对GOUGH研制的并联机构进行改进,并将其应用于飞行模拟器的运动产生装置以来,六自由度平台因其刚度大、承载能力强、精度高等优点,被广泛应用于运动模拟器、并联机床、精密定位平台、空间对接等领域。
直升机悬停救助模拟器用于在陆上实验室中模拟训练救生人员在恶劣海况条件下运用特殊救助装备(专用绞车、红外搜寻、救生衣、救生筏等)进行的直升机悬停救助任务。我国现有S-76+救助直升机25架,分布于11个沿海城市,实行动态待命,以应对突发事件。直升机救助机组训练只能集中到没有海上救援任务时进行,很大程度上限制了训练周期与风险。为此,某大学救助与打捞工程实验室建立了直升机悬停救助系统,相对于实际训练,它具有安全高效、节省成本等优点,是救援训练的重要方式。直升机悬停救助模拟系统由地面上的造浪水池和悬挂在桥式起重机上的救助模拟器组成,其中Stewart并联机构作为直升机模拟机舱的运动产生装置,通过采集真实救助场景下的直升机运动数据,复现直升机悬停运动状态,如图1所示。Stewart并联平台在不同的救助场景有不同运动状态和轨迹,为保证Stewart并联机构在模拟直升机悬停运动时的活动范围不超过平台最大边界范围,同时,保证模拟器机舱与周围环境不产生干涉,需要对Stewart平台的可达工作空间进行计算和分析。

图1 直升机悬停救助模拟平台
工作空间是并联机构末端机构活动所能达到的可能方位,是评价并联机构工作能力的一个重要指标。与串联机构不同,并联机构的工作空间表示的主要问题在于:关于任意自由度的有关限制总是耦合的,很难找到结构尺寸与工作空间的必然联系。对于自由度大于3的机器人,仅当固定-3个位姿参数时,才能图形化地描述工作空间。
目前,计算并联机构工作空间的主要方法有两类:几何方法、数值方法。几何法原理是:确定每个满足一定约束的主动件所有运动范围,所有主动件运动范围的交集就是并联机构的工作空间。几何方法虽然快速和精确,但很难考虑所有约束,必须调整以适应不同研究对象。在数值方法中,工作空间被笛卡尔坐标或极坐标节点网络覆盖,测试每个节点,判断是否属于工作空间。数值方法计算量大,边界精度依和计算时间依赖采样步长。
以上两种方法都不适应直升机悬停救助模拟器需要频繁快速验证各种海况下直升机真实运动数据的应用场合,为此,本文作者提出一种基于运动学正解的工作空间凸包算法。该方法是将并联平台的电动缸行程量均匀分段,运用运动学正解得到并联平台的可达位置坐标点点集,不同于数值方法需要验证每个步长的节点,该方法不需要测试冗余节点,节省了大量运算。由于运动学正解计算获得的可达位置坐标点分布不均匀,分布规律复杂,难于公式化,运用凸包算法将离散的可达位置坐标点空间化,计算出可达工作空间三维边界,研究分段数与三维边界的相关性,进一步减少求解过程中的运算量。
研究内容如下:(1)可达工作空间凸包算法的计算模型,包括Stewart并联机构的运动学正解和凸包算法理论模型;(2)直升机悬停模拟并联平台可达工作空间的计算结果及正确性验证。
1 计算可达工作空间点集
Stewart直升机悬停模拟并联平台主要包括与天车小车连接固定的静平台,与模拟舱连接的动平台,以及6根不带防回转装置的电动缸。平台倒挂于桥式起重机上,静、动平台与电动缸之间通过虎克铰连接。
平台结构参数如图2所示,分别包括静平台铰圆半径、动平台铰圆半径、静平台短边铰间距、动平台短边铰间距、中位缸长、电动缸行程等6个参数。由于Stewart平台的机构特点,根据以上6个参数就可以确定平台的基本结构。、分别为动、静平台的短边夹角。
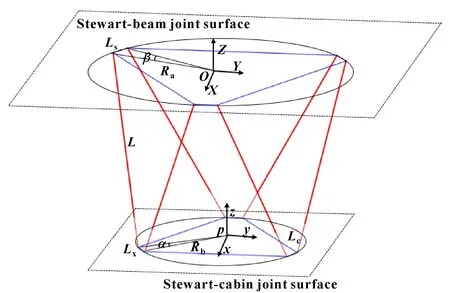
图2 Stewart平台结构示意
Stewart平台的运动正解是指:已知平台6条支腿的长度,求解平台的位置姿态。选取固定不动的静平台铰圆圆心为静坐标系的坐标原点,选取动铰圆圆心为动坐标系的坐标原点,定义平台初始位置为平台中位。在平台每条支腿的长度已知时,根据上、下铰点在静坐标系中的关系,最终可获得6个变量6个方程的非线性方程组。
将6个动铰点在坐标系中坐标用矩阵表示,铰支点在静坐标系中的坐标可用矩阵表示为
=·
(1)
转换矩阵可表示为下式
=
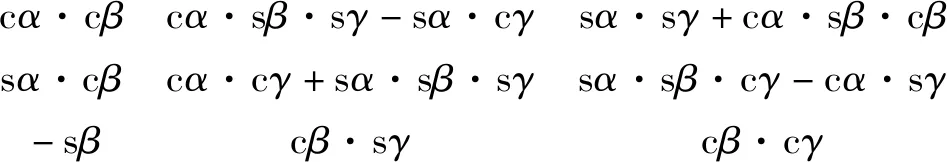
(2)
式中:c表示余弦符号cos ;s表示正弦符号sin。
运动平台的姿态表示为

(3)
其中:为Stewart并联机构静平台在静坐标系的坐标矩阵;为Stewart平台电动缸的长度矩阵。
以Stewart平台中位位姿作为初始点,用牛顿迭代法求解非线性方程组()=0 (=1,2,…,6),即可得到特定支腿长度下的平台位姿。
将Stewart平台6根电动缸的行程均匀分段,分段数为,的数值大小将决定Stewart平台可达工作空间的解算离散点数和求解时间。设定动平台铰圆圆心在静坐标系中的坐标值为平台位姿的位置描述,则每一个离散点代表与之对应的一种Stewart平台位姿。对于分段数为的6条支腿,正解后得到(+1)种平台位姿,用点集表示,方便下一步凸包算法进行空间化筛选。
2 凸包算法
凸包是计算几何中重要的几何结构,把多面体的任何一个面无限延展,其他所有面都在这个延伸面的同一侧,这类多面体叫做凸包。凸包算法要解决的问题是找出包围点集的最小凸区域的边界,其定义为能够包含的最小凸集。
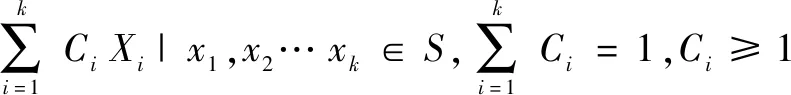
(4)
凸包算法框架如下:
步骤1,凸包初始化。扫描点集,并从中选取4个不共面的点构成四面体。选取原则为:选取坐标轴方向两端极值点构成线段,选取距离线段最远点构成平面,最后选取距离该平面最远点构成四面体,即初始凸包,并构建凸包集合。
步骤2,判断新添加点与凸包的相对位置。随机选取点集中剩余一点,分别与凸包集合中所有三角形平面上一点连接,判断与三角形平面法向量关系,若与所有三角平面都符合≥0,则认为该点在凸包外部,否则舍弃该点,重新选取剩余点。
步骤3,构建新的凸包集合。与凸包集合最近三点构造四面体,并与四面体构成新的凸包集合,如图3所示。

图3 凸包算法示意
步骤4,循环判断点集中剩余的点。重复执行步骤2和步骤3,直到遍历点集所有点,算法结束。最终得到的三维凸包即为Stewart平台的可达工作空间。凸包算法流程如图4所示。

图4 凸包算法流程
3 计算结果及试验
3.1 计算结果
基于MATLAB编写求解程序,交互界面如图5所示,程序输入静平台铰圆半径、动平台铰圆半径、静平台短边铰间距、动平台短边铰间距、中位缸长、电动缸行程等6个参数,可求解出工作空间;更改交互界面输入参数的数值,可求解不同结构参数Stewart并联平台的可达工作空间,分段数用于调节计算时间和计算精度。该程序同时具有干涉检测功能,添加一段直升机悬停救助模拟器运动状态数据,可以绘制模拟器运动轨迹,并与已知平台工作空间进行干涉检测。输入实验室中直升机悬停救助模拟器并联平台参数,=1.05 m、=0.75 m、=0.2 m、=0.15 m、=1.3 m、=0.4 m,调节分段数为4,可显示平台结构和平台的可达工作空间,求得可达工作空间体积为0.137 m。平台最大转动角度计算结果为:横摇角范围为±23°、纵摇角范围±23°、偏航角范围为±25°。

图5 Stewart平台工作空间求解程序
3.2 算法效率
算法求解速度和求解分辨率与点集中点的数量有关。分段数越大,点集中点的数量越多,求解时间越长,求解分辨率越高。程序运行计算机配置如下:Intel Core i5-4460@3.20 GHz、RAM8.00 GB。数值算法采用边界搜索法,以动平台铰圆圆心为起点,将空间按步长划分为离散点,验证每个离散点是否满足支腿长度、转角等限制。图6显示凸包算法计算点的数量与耗时关系曲线,横坐标是离散点的数量,用对数表示,左侧纵坐标为算法耗时。从凸包算法耗时和数值算法耗时两条曲线趋势可以看出:随着计算点数量的增多,两种算法的时间消耗和计算点的数量趋近于线性关系,在相同计算点数条件下,凸包算法耗时仅为数值算法的50%。另一方面,数值算法依赖大量数据的求解,计算点数的数量级通常在百万以上,而凸包算法在几万数量级时,就可以得到体积稳定的工作空间。右侧纵坐标描述了计算点数与可达工作空间的体积大小关系曲线,可以看出:当分段数大于4时,工作空间的体积大小趋于稳定,计算结果不再变化。分段数为4时,点集内点的数量为15 625个,耗时72 s。两种算法效率对比可以看出,不仅在相同计算量的条件下,凸包算法更加快速,并且在实际工程应用中,凸包算法可以用低于数值算法两个数量级的计算量得到体积稳定的工作空间。
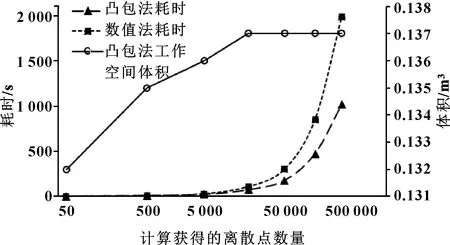
图6 凸包算法计算点的数量与耗时关系
3.3 算法准确度验证
直升机悬停救助模拟器并联平台处于极限位姿时,是并联平台所能达到的最远距离,验证并联平台处于极限位姿时动平台圆心在求解的可达工作空间的边界上,即可证明程序的准确性。分别对并联平台的15个极限位姿时动平台圆心位置进行验证,结果显示:当并联平台处于沿空间坐标轴平移的极限位姿时,动平台圆心位于计算得出的可达工作空间边界之上;当并联平台处于绕空间坐标轴转动的极限位姿时,动平台圆心在可达工作空间边界之内。图7为其中4组试验结果,动平台圆心为黑色圆点。

图7 并联平台极限位姿与可达工作空间位置关系
同时,对Stewart平台可达工作空间的求解结果进行实验验证。由于零姿态角时Stewart平台的工作空间最大,实验方案选择测量在动平台姿态角为(0,0,0)时,平面和平面处可达工作空间边界的坐标值。首先固定轴坐标为0,将直升机悬停救助模拟器分别沿轴和轴方向移动,使其处于极限位姿,此时选取动平台圆心为测量点,测量圆心分别距离平面和平面的数值,可以得到两个测量位置。将悬停救助模拟器回归到初始位置,按上述操作对轴方向每隔0.05 m进行一轮测量,共可以得到22个测量位置。将直升机悬停救助模拟器移动到测量平台可达空间边界值,并与通过正解包络法计算得到的边界值进行对比,误差为正表示计算值比测量值大,误差为负表示计算值比测量值小。结果显示:正解包络法在平台可达工作空间的上下两端精度较高,误差为1%左右,在工作空间中部误差较大,且为正误差,误差在5%以内。
分别在平面和平面的轴方向均匀选取11个测量点,测量平台可达空间边界值,并与通过正解包络法计算得到的边界值进行对比,误差为正表示计算值比测量值大,误差为负表示计算值比测量值小。表1结果显示:正解包络法在平台可达工作空间的上下两端精度较高,误差为1%左右,在工作空间中部误差较大,且为正误差,误差在5%以内。
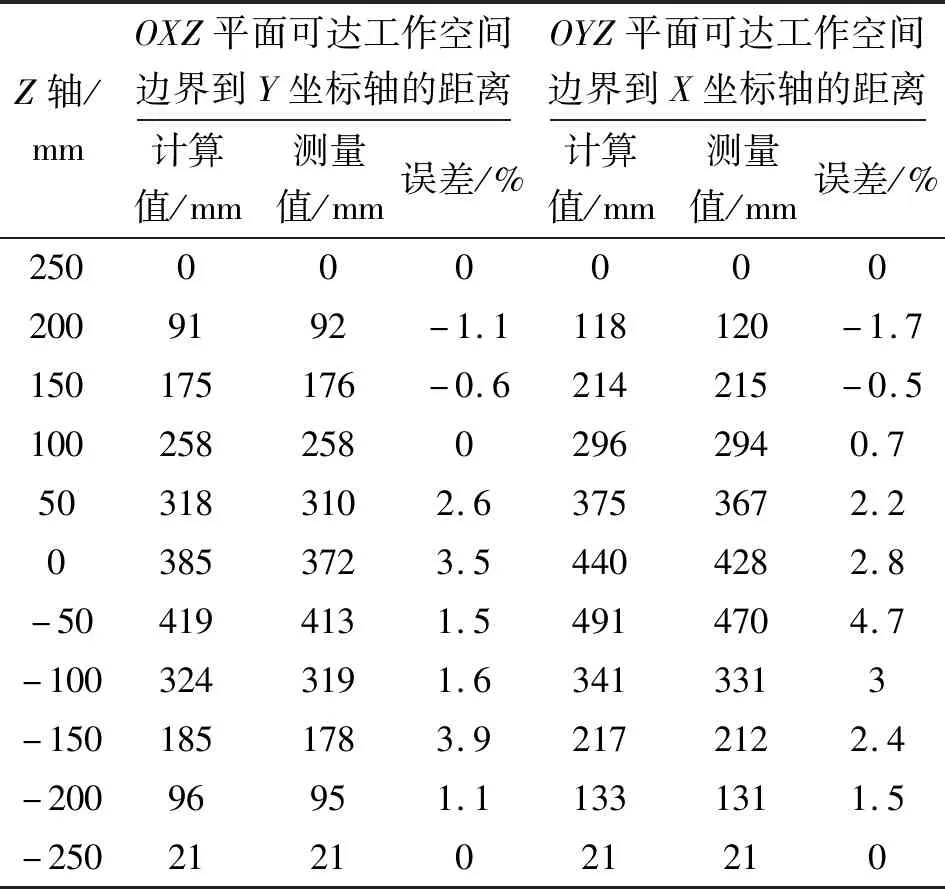
表1 可达工作空间计算值与测量值对比
4 结论
提出一种基于Stewart并联平台运动学正解和凸包算法结合的可达工作空间求解方法:将平台6条支腿伸长量离散化,用运动学正解得到并联平台的可达位置坐标点点集,结合凸包算法将离散的可达位置坐标点空间化,计算出可达工作空间三维边界,并通过研究分段数与三维边界的相关性,进一步减少求解过程中的运算量。
该方法与常用可达空间求解方法相比,不必预设工作空间范围后预测各个节点,减少了大量冗余计算,对于一般Stewart平台,1 min左右就可以计算得到可达工作空间的三维参数;同时,该方法具有较好的精确度,两端误差1%,最大误差在5%以内。对直升机悬停救助模拟器不同工况下运动轨迹的干涉检测提供了依据,为以后建立类似救助模拟器提供了参考。

