Secondary electron emission model for photo-emission from metals in the vacuum ultraviolet
Ai-Gen Xie· Yi-Fan Liu· Hong-Jie Dong
Abstract This study investigates two secondary electron emission (SEE) models for photoelectric energy distribution curves f(Eph, hγ), B, Emean, absolute quantum efficiency(AQE),and the mean escape depth of photo-emitted electrons λ of metals. The proposed models are developed from the density of states and the theories of photo-emission in the vacuum ultraviolet and SEE, where B is the mean probability that an internal photo-emitted electron escapes into vacuum upon reaching the emission surface of the metal, and Emean is the mean energy of photo-emitted electrons measured from vacuum. The formulas for f(Eph,hγ),B,λ,Emean,and AQE that were obtained were shown to be correct for the cases of Au at hγ = 8.1–11.6 eV, Ni at hγ = 9.2–11.6 eV, and Cu at hγ = 7.7–11.6 eV. The photoelectric cross sections (PCS) calculated here are analyzed, and it was confirmed that the calculated PCS of the electrons in the conduction band of Au at hγ = 8.1–11.6 eV, Ni at hγ = 9.2–11.6 eV, and Cu at hγ = 7.7–11.6 eV are correct.
Keywords Absolute quantum efficiency · Photoelectric cross section · Mean escape depth of photo-emitted electrons · Probability · Photo-emission from metals ·Secondary electron emission · Vacuum ultraviolet · Mean energy of photo-emitted electrons
1 Introduction
The photoelectric effect is important in various domains,such as astrophysics,material analysis applications,photon science,interactions between photons and materials,photomultipliers, photo-injectors such as RF photo-cathode gun in accelerators, and X-ray sources [1–3]. Photoelectric energy distribution curves f(Eph, hγ) can be used to characterize the properties of the photoelectric effect,Ephis the energy of hγ photon-induced electrons with E measured from the bottom of the conduction band of metal, E is the initial energy of electrons measured from the bottom of the conduction band of metal,h is the Plank constant, and γ is the photon frequency. Thus, many researchers have investigated f(Eph, hγ) [4, 5]. From the fact that SEE and photo-emissions have the same escape and transport mechanisms [6, 7] and the characteristics of electronphoton interaction and propagation of photons, two formulas for f(Eph, hγ) from metals in the vacuum ultraviolet have been obtained. Further, the value of f(Eph, hγ)obtained from Au at hγ = 8.1–11.6 eV, Ni at hγ =9.2–11.6 eV, and Cu at hγ = 7.7–11.6 eV have been proven to be true.
The absolute quantum efficiency (AQE)(hγ) and quantum efficiency (QE)(hγ) are important parameters that are used to characterize photo-emission ability [8–10]. The mean probability that an internal photo-emitted electron escapes into vacuum upon reaching the emission surface of metal B and λ is important parameter of AQE(hγ) and QE(hγ), where λ denotes the mean escape depth of photoemitted electrons.The B is inaccessible to measure;further,the formula for B and λ has not yet been deduced. It is difficult to measure λ, and the relative differences among the λ values measured by different authors can reach about 100% or more [11–13]. Thus, there is the need for theoretical studies of B and λ.The value of the mean energy of photo-emitted electrons Emeanmeasured from vacuum is an important parameter to assess the mechanisms of energy loss of internal photo-emitted electrons.The internal photoemitted electrons lose energy mainly by electron–phonon scattering for the case of Emean<1.0 eV; however, they lose energy mainly by electron–electron scattering[13]for the case of Emean>1.0 eV. From the two formulas for f(Eph,hγ)deduced here and the definitions of B,Emean,and λ,the respective formulas for B,λ,and Emeanfor metals in the vacuum ultraviolet have been deduced. Based on the fact that the deduced formulas for f(Eph,hγ)obtained from Au, Ni, and Cu have been experimentally proven and the courses of deducing the formulas for B, Emean, and λ from metals,it can be concluded that B,Emean,and λ from Au at hγ = 8.1–11.6 eV, Ni at hγ = 9.2–11.6 eV, and Cu at hγ = 7.7–11.6 eV calculated with corresponding deduced formulas are correct.
Photoelectric cross section PCS is an important topic[14–16], and it has been investigated by many researchers PCS[17].However,owing to the complexity and difficulty of researching PCS at hγ <50 eV, there are few reported values of measured and calculated PCS at hγ <50 eV[18].Furthermore, the relative differences among the PCS values at hγ <50 eV obtained by different authors can reach about 200% or more [19]. Thus, it is important to present accurate methods of determining PCS at hγ <50 eV.From the energy band structures of metals, the definition of AQE(hγ), and one of the formulas for f(Eph, hγ) deduced here, the formula for AQE(hγ) from metals in the vacuum ultraviolet as a function of the density of states, PCS, Aα,Φ, EF, Eph, hγ, s and ρ has been deduced, where Aαis the molar mass of an atom, ρ is the material density, Φ is the work function, EFis the distance from the bottom of conduction band to Fermi level, and s denotes the number of electrons of conduction band that is provided by one atom.Using the deduced formula for AQE(hγ), experimental AQE(hγ)[20,21],and known parameters such as density of states, Aα, Φ, EF, hγ, s, and ρ, the PCS of the electrons in the conduction band of Au at hγ = 8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV are calculated.These calculated PCS are analyzed, and it can be concluded that the calculated PCS of the electrons in the conduction band of Au at hγ =8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV are correct, and that the method presented here of calculating PCS with the deduced formula for AQE(hγ) is a very accurate method.
According to the simple theories of SEE, the fact that SEE and photo-emission have common escape and transport mechanisms [6, 7], and the definition of AQE(hγ), the universal formula for AQE(hγ) has also been deduced. For negative electron affinity semiconductors (NEAS), the deduced universal formula for AQE(hγ) has the same expression as the existing formula for AQE(hγ) obtained from NEAS used in some studies [22–24]. The method of calculating PCS using the deduced universal formula for AQE(hγ) as well as parameters such as experimental AQE(hγ) [20, 21, 25], B, and λ is also presented. The PCS of the electrons in the conduction band of Au, Ni, and Cu are calculated using this method and are analyzed.It can be concluded that the calculated PCS of the electrons in the conduction band of Au at hγ = 8.1–11.6 eV, Ni at hγ =9.2–11.6 eV,and Cu at hγ = 7.7–11.6 eV are correct,and that the proposed method of calculating PCS using the deduced universal formula for AQE(hγ) is more accurate.
2 Processes of photo-emission
When N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals,the number of incident photons at x can be written as follows [13, 26, 27]:

where x is the distance from the incident surface to the position at which the photons arrive, N0is the number of incident photons at x = 0, and αγis the optical absorption coefficient at γ. From the energy band structures of metals shown in Fig. 1 (Egis the distance from the top of the valence band to the bottom of the conduction band of metals), the quantum theory, and law of energy conservation, it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals,only the electrons in the conduction band of the metal can be excited by the photons.
According to the characteristics of electron-photon interaction, it is known that the probability that all of the electrons in the same energy band of a given metal absorb one photon at a given γ can be approximated as a constant[14, 28, 29]. Thus, the probability that the electron in the conduction band of a given metal absorbs one photon at a given γ can be approximated as a constant Cγ. That is, the PCS at a given γ of the electrons in the conduction band of a given metal can be approximated as a constant Cγ.Based on the energy band structures of metal shown in Fig. 1,the calculated number of electrons per atom per eV g(E)[20, 21, 25], the values of EF, the law of energyconservation, and the fact that γ is <(EF+ Eg)/h, we can calculate the relative number of electrons in the conduction band of a metal that may absorb one photon and become photo-excited electrons. For example, when the photons at hγ = 7.4 eV enter Au with EF= 11.6 eV[20],the electrons with E ≥(EF7.4 eV) (i.e., 4.2 eV) may absorb one photon and become photo-excited electrons. Thus, based on the g(E) value of Au [20], the fact that the electrons with E ≥4.2 eV may become photo-excited electrons and the fact that the EFvalue of Au equals 11.6 eV, we can obtain n%of electrons in the conduction band of Au, which may absorb one photon and become photo-excited electrons based on calculations, and the obtained n% for Au at hγ = 7.4 eV equals 0.808; using the same method, we obtain n%at different hγ values of Au,Ni,and Cu,and the corresponding results are shown in Tables 1, 2, and 5,respectively.Therefore,from the definition of αγ[13,26]in Eq. (1)and the fact that the probability that the electron in the conduction band of a given metal absorbs one photon at a given γ can be considered as a constant Cγ, the αγparameter of Eq. (1) can be written as

Fig. 1 Schematic energy band structures of metals

The unit of ρ is g/m3, the unit of Aαis g/mol, and NAdenotes the Avogadro constant.
Based on the fact that Ephis the energy of hγ photoninduced electrons with E measured from the bottom of the conduction band of a metal, the relation E = Ephhγ is obtained. Some authors have calculated g(E) [20, 21, 25]and the energy distribution of electrons in the conduction band of metal with V = 1.0 m3G(E) (i.e., density of states of conduction band of metal) [30, 31]. According to the definitions of G(E)and g(E)and the relation E = Ephhγ,therelation between G(E) and g(E)(i.e., the relation G(Ephhγ)and g(Ephhγ)) can be written as [30, 31]

Table 1 The parameters of Au calculated using the first SEE model

Table 2 The parameters of Ni calculated using the first SEE model

Processes involved in photo-emission may be considered as three-step processes[21]:first,electrons are excited to become internal photo-emitted electrons; second, a portion of the internal photo-emitted electrons propagate to the emission surface; and third, a portion of the internal photo-emitted electrons reaching the emission surface escape into the vacuum and become photo-emitted electrons. The three-step processes of photo-emission from metal which are investigated in detail in this work are as follows:
Owing to the fact that the PCS for a given γ value of the electrons in the conduction band of a given metal can be considered as a constant Cγ, definitions of αphγ, G(Ephhγ),and g(Ephhγ) [13, 26, 30, 31] and Eqs. (1) and (3), in the case that N photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the number of internal photo-emitted electrons at x per unit path length of incident photons can be written as:

where αphγis the photoelectric absorption coefficient at γ.
Most secondary electrons have energy Evac>1.0 eV[32, 33], and the mean energy of secondary electrons emitted from metal Eamis much larger than 1.0 eV, and both Evacand Eamare measured from vacuum. In the case that Eamis much larger than 1.0 eV,the mean escape depth of secondary electrons with E0(0 ≤(E0Φ–EF≤1.5EF)) in metals can be expressed as [34, 35]

where E0is measured from the bottom of the conduction band,and E0is the sum of E and the energy obtained from primary electrons by scattering. The unit of length in this study is m, but the unit of length in Refs. [34, 35] is A˚.Therefore, in this study, the magnitude of the formula coefficient in Refs. [34, 35] is 1010times that in Eq. (5).
According to the energy band structures of metals,the fact that the electrons with E absorbing one hγ photon have(E + hγ)(i.e., Eph) and the theories of photo-emission, we estimate that in the case that γ is farther away γ0{ i.e.,γ >[(3.0 eV/h) + γ0]}, most of the hγ photon-induced electrons in metals have Evac>1.0 eV,and Emeanis much larger than 1.0 eV,where γ0is the threshold frequency.Thus,from the fact that SEE and photo-emission have common escape and transport mechanisms[6,7]and the fact that most secondary electrons in metals also have Evac>1.0 eV and Eamis also much larger than 1.0 eV,it is known that the hγ photon-induced electrons with Ephthat undergo photoemission from metals farther than γ0have the same transport mechanisms as do secondary electrons in metals.Further,the mean escape depth of hγ photon-induced electrons with Ephthat undergo photo-emission from metals farther away than γ0λ(Eph, hγ) has a similar expression as does Eq. (5).Therefore,according to Eq. (5)and the fact that the electrons with E absorbing one hγ photon have an Ephvalue that corresponds to E0,in the case where Emeanis much larger than 1.0 eV,λ(Eph,hγ)can be written as

The probability that an internal secondary electron having E0≥(Φ + EF) and reaching an emission surface passes over the surface barrier of a metal into a vacuum[34–36] is expressed as
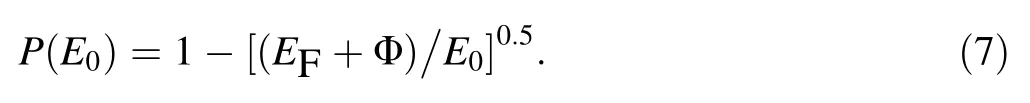
From Eq. (7),the fact that photo-emission and SEE have common escape mechanisms [6, 7] and the fact that E0corresponds to Eph= E + hγ, the probability that an internal photo-emitted electron with E absorbing one hγ photon, having Eph≥(Φ + EF) and reaching an emission surface passes over the surface barrier of metal can be written as [36, 37]

Based on Eqs. (6) and (8), the probability that an internal photo-emitted electron with E, which absorbs one hγ photon and is excited at x,can reach an emission surface and pass over the surface can be written as

3 First SEE model for photo-emission
Based on the fact that SEE has a maximum escape depth that is five times the mean escape depth[34,35,37],it is easy to understand that this is also applicable for photo-emitted electrons because both of them have common escape and transport mechanisms[6,7].Thus,f(Eph,hγ)can be given as

where λrealof Eq. (10) can be written as

Based on the energy band structures of metals shown in Fig. 1, Eq. (8), and the fact that the electrons with E absorbing one hγ photon have Eph= (E + hγ),it is known that in the case that N0photons at γ <(EF+ Eg)/h enter into metals,the electrons with E in the range of[(EF+ Φ–hγ), (EF+ Φ)] absorbing one hγ photon have Ephin the range of [(EF+ Φ), (EF+ Φ + hγ)], and that the photoemitted electrons with Ephin the range of [(EF+ Φ),(EF+ Φ + hγ)] may escape into the vacuum. Thus, from Eq. (10), it is known that in the case that N photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the number of photo-emitted electrons can be written as

AQE(hγ) is defined as the number of photo-emitted electrons per absorbed photon [38, 39]. Thus, from the definition of AQE(hγ), the fact that N0photons at γ <(EF+ Eg)/h are absorbed by metals and Eq. (12), the AQE(hγ) from metals induced by photons at γ <(EF-+ Eg)/h can be written as

From Ref.[20],it is known that the g(E)(i.e.,g(Ephhγ))of Au is as shown in Fig. 1 of Ref.20,and that the s,EF,and Φ values of Au equal 11, 11.6 eV, and 4.9 eV, respectively.The Cγvalue of Au calculated with parameters (hγ, NA, s,ρ = 1.93 × 107g/m3, Aα= 197 g/mol [40], g(Ephhγ) [20],EF,Φ,n%and experimental AQE(hγ)[20]shown in Table 1)and Eqs.(2),(6),(11),and(13)are still shown in Table 1.The λγvalue of Au calculated using Eq. (2) and parameters (s,NA,ρ,Aα,n%,and Cγshown in Table 1)are also shown in Table 1.The values of f(Eph,hγ)(in arbitrary units)of Au are calculated with parameters(Eph,hγ,g(Ephhγ),EF,Φ,λγ,and Cγ, as shown in Table 1) and Eqs. (6), (10), and (11). The comparison between these calculated f(Eph,hγ)values of Au and the experimental ones[20]is shown in Fig. 2.

Fig. 2 Comparison between the f(Eph, hγ) values of Au calculated using Eq. (10) and experimentally obtained values
From Ref.[21],it is known that the g(Ephhγ)value of Ni is asshowninFig. 18ofRef.[21],andthatthes,EF,andΦvalues of Ni equal 10,6.0 eV,and 5.0 eV,respectively.The Cγat hγ≤11.0 eV of Ni calculated with parameters (hγ, NA, s,ρ = 8.9 × 106g/m3,Aα= 58.69 g/mol[40],g(Ephhγ)[21],EF,Φ,n%,and AQE(hγ)[21]shown in Table 2)and Eqs.(2),(6),(11),and(13)areasshowninTable2.ThesumofEFandΦ of Ni is equal to 11.0 eV. Thus, from Fig. 1, when we use parameters(hγ,NA,s,ρ,Aα,g(Ephhγ),EF,Φ,n%,and experimentalAQE(hγ)[21]showninTable2)andEqs.(2),(6),(11),and(13)tocalculatethevalueofCγathγ >11.0 eVforNi,the lower limit of the integral[i.e.,(EF+ Φ)]in Eq. (13)should be replaced with‘‘hγ’’.The λγof Ni calculated with Eq. (2)andparameters(s,NA,ρ,Aα,n%,andCγshowninTable2)are also shown in Table 2.The f(Eph,hγ)value(in arbitrary units)of Ni calculated with corresponding parameters (Eph, hγ,g(Ephhγ),EF,Φ,λγ,and Cγshown in Table 2)and Eqs.(6),(10),and(11)are shown in Fig. 3.
Based on Eq. (12) and three-step processes of photoemission, it is known that in the case where N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the number of internal photo-emitted electrons reaching the surface can be written as


Fig. 3 The f(Eph, hγ) values calculated using Eqs. (10) and Eq. (21) for Ni
Based on Eqs. (6) and (12), it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the total escape depth of photo-emitted electrons can be written as

According to Eq. (12) and the fact that the photo-emitted electrons with E absorbing one hγ photon have Evac-= (Eph–EF–Φ),it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the total Evacof photo-emitted electrons can be written as

Based on the definition of B and Eqs. (12) and (14), B can be expressed as

From the definition of λ and Eqs.(12)and(15),λ can be written as

Based on the definition of λ and Eqs. (12) and (16),Emeancan be expressed as

The B values of Au and Ni are calculated using Eqs.(6),(11),(12),(14),and(17)and corresponding parameters(hγ,g(Ephhγ),EF,Φ,λγshown in Tables 1,2),respectively;The λ values of Au and Ni are calculated using Eqs. (6), (11),(12), (15), and (18) and corresponding parameters (hγ,g(Ephhγ), EF, Φ, λγshown in Tables 1 and 2). The Emeanvalues of Au and Ni are calculated using Eqs. (6), (11),(12), (16), and (19), and corresponding parameters (hγ,g(Ephhγ), EF, Φ, λγshown in Tables 1 and 2). These calculated B, λ, and Emeanvalues of Au and Ni are shown in Tables 1 and 2.
The sum of the EFand Φ values of Ni is equal to 11.0 eV [21]. Thus, in the case that photons at hγ >11.0 eV enter Ni,the electrons in the conduction band absorbing one hγ photon at least have Eph= hγ. Therefore, when we use Eqs. (12) and (14)–(19) to calculate the corresponding parameters (B, λ and Emean) at hγ >11.0 eV for Ni, the lower limit of the integral in Eqs.(12)and(14)–(16)should be replaced with ‘‘hγ’’. These calculated B, λ and Emeanvalues of Ni are shown in Table 2.
From the energy band structures of metal shown in Fig. 1, the law of energy conservation, the relation of Eph= E + hγ,and the courses of deducing Eqs.(12)–(16),it is known that in the case that hγ is within the range of((EF+ Φ), (EF+ Eg)), the lower limit of the integral in Eqs. (12)–(16) should be replaced with ‘‘hγ’’.
4 Second SEE model for photo-emission
From the above courses of calculating Cγwith Eqs. (2),(6), (11), and (13), it is known that in the cases that the AQE(hγ) or absolute g(Ephhγ) values are not known, Cγcannot be calculated using Eqs. (2), (6), (11), and (13).From the above courses of calculating λγ, f(Eph, hγ), B, λ and Emean, it is also known that λγ, f(Eph, hγ), B, λ, and Emeancan be calculated by the first SEE model for photoemission on the basis of the known Cγ. Thus, in the case that AQE(hγ) or the absolute g(Ephhγ) value is not known,λγ, f(Eph, hγ), B, λ, and Emeancannot be calculated by the first SEE model either.Therefore,we present the following second SEE model for f(Eph,hγ),Cγ,λγ,B,λ,and Emeanof metals; in the case that both AQE(hγ) and the absolute g(Ephhγ) values are not known, f(Eph, hγ), B, λ, and Emeancan still be calculated by the second SEE model.In the case that the absolute g(Ephhγ) value is not known, Cγand λγcan still be calculated by the second SEE model.
Suppose that in the case that N0photons at γ <(EF-+ Eg)/h enter perpendicularly into metals, the number of photons at x does not decrease with increasing x, and equals N0. Thus, based on Eq. (3), the above assumption,and the fact that the PCS at a given γ of the electron in the conduction band of a given metal can be considered as a constant Cγ,in the case that N0photons at γ <(EF+ Eg)/h enter into metals, the number of internal photo-emitted electrons per unit path length of incident photons can be written as

Therefore, from the three-step processes of photoemission,the conclusion that the maximum escape depth of internal photo-emitted electrons with Ephequals 5.0 λ(Eph,hγ) and Eqs. (9) and (20), f(Eph, hγ) can be expressed as

The f(Eph, hγ) (in arbitrary units) values of Au are calculated with corresponding parameters (Eph, hγ, g(Ephhγ)[20], EF, Φ) and Eqs. (6) and (21). The comparison between these calculated f(Eph, hγ) values of Au and experimental ones [20] are shown in Fig. 4. The f(Eph, hγ)value (in arbitrary units) of Ni calculated using corresponding parameters (Eph, hγ, g(Ephhγ) [21], EF, Φ) and Eqs.(6)and(21)are also shown in Fig. 3.From Ref.[25],it is known that the g(Ephhγ)value(in arbitrary units)of Cu is shown in Fig. 4 of Ref. [25], and that the EF, s, and Φ values of Cu equal 12.0 eV, 11, and 4.5 eV, respectively.The f(Eph, hγ) values (in arbitrary units) of Cu are calculated with corresponding parameters (Eph, hγ, g(Ephhγ)[25], EF, Φ) and Eqs. (6) and (21). Comparisons between these calculated f(Eph, hγ) of Cu and corresponding experimental ones [25] are shown in Fig. 5.
In the case that N0photons at γ <(EF+ Eg)/h enter into metals, the electrons with E in the range of [(EF+ Φhγ),(EF+ Φ)] absorbing one hγ photon have Ephin the range of [(EF+ Φ), (EF+ Φ + hγ)], and the photo-emitted electrons with Ephin the range of [(EF+ Φ), (EF-+ Φ + hγ)] may escape into vacuum. Thus, from Eq. (21), it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the number of photo-emitted electrons can be written as

Fig. 4 Comparisons between the f(Eph, hγ) values of Au calculated using Eq. (21) and experimental ones

Equations (21)–(22) are deduced on the basis of the assumption that the number of photons at any x equals N0,but in fact, the number of photons at x decreases with increasing x. Thus, from the characteristics of electron emission and the prerequisite of deducing Eq. (22), it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the real number of photo-emitted electrons is less than the value of Eq. (22)and should be written as

Fig. 5 Comparisons between the f(Eph, hγ) values of Cu calculated using Eq. (21) and experimental ones

For a given γ and metal, K(γ) is a constant that is less than 1.0.
According to Eq. (23) and the three-step processes of photo-emission,it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the number of internal photo-excited electrons reaching the emission surface can be written as
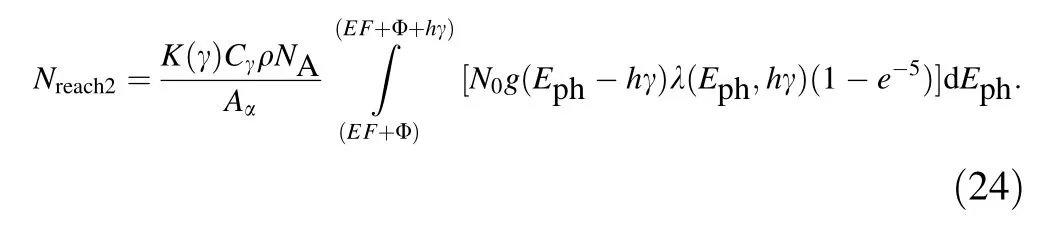
Based on Eqs. (6) and (23), it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the total escape depth of photo-emitted electrons can be written as
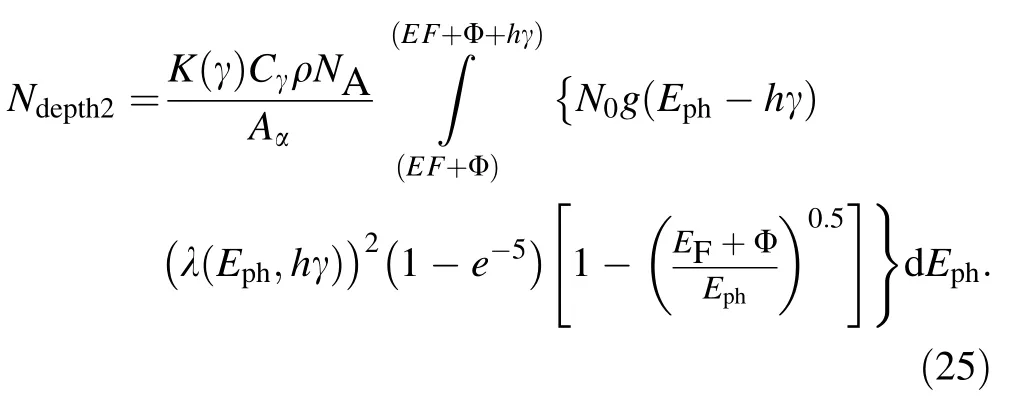
According to the fact that the photo-emitted electrons with E have Evac= (Eph–EF–Φ) and Eq. (23), it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals,the total Evacof photo-emitted electrons can be written as

Based on the definition of B and Eqs. (23) and (24), B can be expressed as

Based on the definition of λ and Eqs. (23) and (25), λ can be written as

Based on the definition of λ and Eqs. (23) and (26),Emeancan be expressed as

The B values of Au calculated with parameters of Au(hγ, g(Ephhγ), EFand Φ) and Eqs. (6), (23), (24), and (27)are shown in Table 3. The λ values of Au calculated with parameters of Au (hγ, g(Ephhγ), EFand Φ) and Eqs. (6),(23),(25)and(28)are shown in Table 3.The Emeanvalues of Au calculated with parameters of Au (hγ, g(Ephhγ), EFand Φ) and Eqs. (6), (23), (26) and (29) are shown in Table 3.Using the same method,the B,λ,and Emeanvalues of Ni and Cu are calculated and shown in Tables 4 and 5,respectively.
As is done for the first SEE model,the lower limit of the integral in Eqs. (23)–(26) should be replaced with ‘‘hγ’’when calculating the corresponding parameters (B, λ and Emean) at hγ >11.0 eV for Ni.
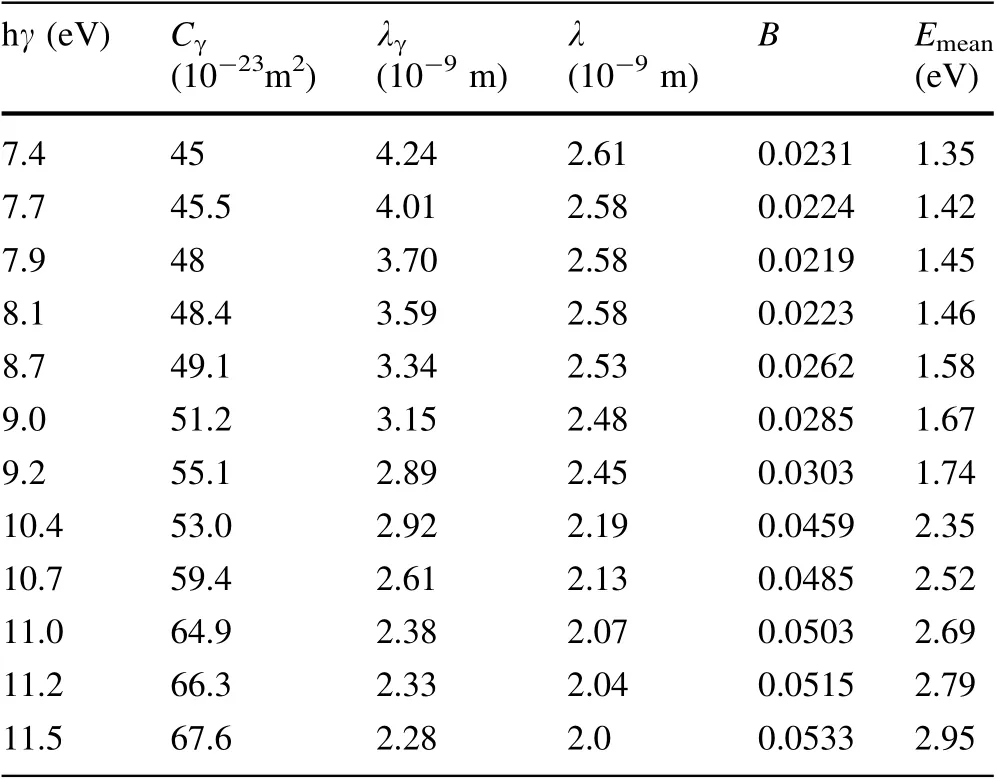
Table 3 The parameters of Au calculated using the second SEE model

Table 4 The parameters of Ni calculated using the second SEE model
According to the simple theories of transport and escape of internal secondary electrons, the probability that an internal secondary electron,which is excited at x,can reach the emission surface and pass over the surface barrier of a metal into vacuum can be written as [41–44]

where Bsis the mean probability that an internal secondary electron escapes into vacuum upon reaching the emission surface, and λsis the mean escape depth of secondary electrons.
Based on Eq. (30) and the fact that SEEs and photoemission have common mechanisms of transport and escape [6, 7], similarly, the probability that an internal photo-emitted electron,which is excited at x,can reach the emission surface and pass over the surface barrier of metal can be written as

Thus, according to the three-step processes of photoemission and Eqs.(4)and(31),it is known that in the case that N0photons at γ <(EF+ Eg)/h enter perpendicularly into metals, the number of photo-emitted electrons can be written as

Therefore,from Eq. (32)and the definition of AQE(hγ),the AQE(hγ) can be written as

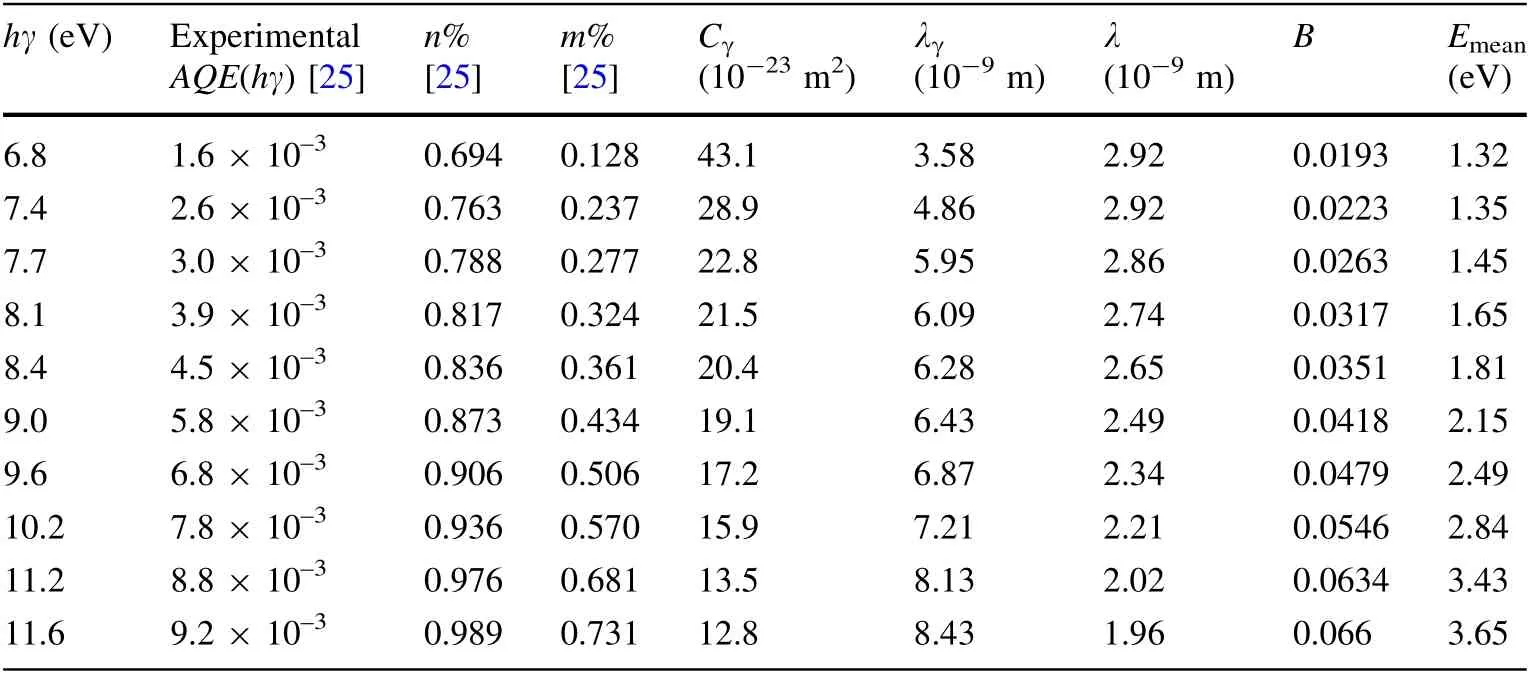
Table 5 The parameters of Cu calculated using the second SEE model
Based on the energy band structures of metal shown in Fig. 1,the calculated g(E),the values of EFand Φ,the law of energy conservation,and the fact that γ is <(EF+ Eg)/h, we can calculate the relative number of electrons in the conduction band of a metal which may absorb one photon and become internal photo-emitted electrons.For example,when the photons at hγ = 7.4 eV enter into Au with EF-= 11.6 eV and Φ = 4.9 eV, it is known that the electrons absorbing one photon and having E ≥[EF–(7.4 eV–Φ)](i.e., 9.1 eV) may have enough energy to become internal photo-emitted electrons. Thus, based on the g(E) value of Au, the fact that the electrons with E 9.1 eV may become internal photo-emitted electrons and the fact that the EFand Φ values of Au equal 11.6 eV and 4.9 eV,respectively,we can calculate the m% electrons in the conduction band of Au which may absorb one photon and become internal photo-emitted electrons by calculating, and the calculated m% at hγ = 7.4 eV of Au equals 0.0734. Using the same method, the m% at different hγ values of Au, Ni, and Cu can be calculated and are shown in Tables 1, 2, and 5,respectively. Therefore, from the definition of αphγand the fact that the probability that the electron in the conduction band of a given metal absorbs one photon at a given γ can be considered as a constant Cγ, in the case that photons at γ <(EF+ Eg)/h enter perpendicularly into metals,the αphγvalue of Eq. (33) can be expressed as

Note that in the case that photons at γ <(EF+ Eg)/h enter perpendicularly into metals,the αγvalue of Eq. (33)is expressed as Eq. (2).
αγof NEAS equals αphγ[22–24]. Thus, from Eq. (33),AQE(hγ) from NEAS can be written as

It is well known that excited electrons (including electron-induced electrons, ion-induced electrons, and photoexcited electrons) with different E values have different values of mean escape depth and mean escape probability[6, 7, 13, 26, 32–37, 45]. Thus, from the physical mechanisms of transport and escape of excited electrons, it is known that the process that Eqs. (30)–(31) use to express f(x)in the courses of deducing some formulas[41–44]is an approximate process; where f(x) is the probability that an electron excited at x escapes into a vacuum.In other words,there is the approximation that Eq. (31) is used to express f(x)phmade in the courses of deducing Eq. (33). Equation (6)is derived from Eq. (5),which is correct[34,35]in the case that Eamis much larger than 1.0 eV, and Eq. (8)and Eq. (31)are derived from Eq. (7)[36,37]and Eq. (30)[41–44], which are also correct. Thus, Eqs. (6), (8), and(31) are correct. Therefore, from the fact there is an approximation made while deducing Eq. (33)and Eqs.(13)and (33), it can be concluded that Eq. (13) in the case that Emeanis much larger than 1.0 eV and (32) is theoretically correct, and that Eq. (13) in the case that Emeanis much larger than 1.0 eV is more accurate than Eq. (33).
Some authors assumed that the negative electron affinity photo-emission process can be described by a diffusion model in which AQE(hγ) from NEAS can be expressed as Eq. (35) [22–24], and they successfully used Eq. (35) to analyze the parameters of the negative electron affinity photo-emission[22–24].That is,Eq. (35)is experimentally proven. Thus, from deducing Eqs. (33) and Eq. (35), the conclusion that Eq. (33) is theoretically correct and the relation between Eq. (33)and Eq. (35),it can be concluded that Eq. (33) is further proven to be correct.
5 Results and discussion
It can be seen from Fig. 2 that the calculated f(Eph, hγ)values of Au agree well with the experimental ones[20]at hγ = 8.1–11.6 eV, but not at hγ = 7.4–7.9 eV. It can also be seen from Fig. 3 and the calculated f(Eph, hγ) value of Ni in Fig. 13 of Ref.[21]that both calculations of Ni are in good agreement at hγ = 9.2–11.6 eV, but not at hγ =7.6–8.6 eV.Thus,it can be concluded that Eq. (10)can be used to express the f(Eph,hγ)from Au at hγ = 8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV, and that Eq. (10) can at least express the relative number of photo-emitted electrons with Ephin the cases that N0photons at hγ = 8.1–11.6 eV enter into Au and that N0photons at hγ = 9.2–11.6 eV enter into Ni. Therefore, according to the relation between Eq. (10)and Eqs. (12)–(16), it is concluded that Eqs. (12)–(16) can at least be used to express the relative values of Nelectrons,AQE(hγ), Nreach, Ndepth, and Nenergyfrom Au at hγ =8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV. Then, from Eqs.(17)–(19),it can be concluded that Eqs.(17)–(19)can be used to calculate the B, λ, and Emeanvalues of Au at hγ = 8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV, respectively. That is, the B, λ, and Emeanvalues of Au at hγ =8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV calculated with Eqs. (17)–(19) and shown in Tables 1 and 2 are correct.
The AQE(hγ) values from Au and Ni are calculated using Eqs. (2), (33), and (34) as well as corresponding parameters(s,NA,ρ,Aα,B,λ,Cγcalculated using Eq. (13),m%, and n% shown in Tables 1 and 2). Further, the calculated AQE(hγ) values from Au and Ni are shown in Tables 1 and 2. From Tables 1 and 2, it is known that the calculated AQE(hγ)from Au at hγ = 7.4–11.5 eV and Ni at hγ = 7.6–11.6 eV are in agreement with the corresponding experimental ones[20,21].Thus,from the conclusions that the B and λ of Au at hγ = 8.1–11.5 eV and Ni at hγ =9.2–11.6 eV calculated with Eqs. (17)–(18) are correct,and the conclusion that Eq. (33) is correct, it can be concluded that the Cγvalues of Au at hγ = 8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV calculated with Eq. (13) are correct.Therefore, from the conclusions that Eq. (13) can at least be used to express the relative values of AQE(hγ)from Au at hγ = 8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV, it can be concluded that Eq. (13) can also be used to express the absolute values of AQE(hγ) from Au at hγ = 8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV. From the conclusions that the Cγvalues of Au at hγ = 8.1–11.5 eV and Ni at hγ =9.2–11.6 eV calculated with Eq. (13) are correct, and the fact that the λγvalues of Au and Ni are calculated with Eq. (2) and corresponding Cγcalculated with Eq. (13), it can be concluded that the λγvalues of Au at hγ =8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV calculated with Eq. (2) are also correct.
From the conclusion that the Cγvalues of Ni at hγ =9.2–11.6 eV calculated with Eq. (13) are correct and the fact that the λγvalues of Ni are calculated with Eq. (2)and the Cγvalues of Ni calculated with Eq. (13), it can be concluded that the λγof Ni at hγ = 9.2–11.6 eV calculated with Eq. (2) is also correct. From the comparison between the calculated AQE(hγ) from Au at hγ = 8.1–11.5 eV and AQE(hγ)from Ni at hγ = 9.2–11.6 eV shown in Tables 1,2 and experimental ones [20, 21] shown in Tables 1, 2, it is known that the relative differences between the calculated AQE(hγ) and experimental ones [20, 21] are within the range of 5–15%.From the conclusion that Eq. (13)is more accurate than Eq. (33), it can be assumed that the differences between experimental AQE(hγ) and ones calculated with Eq. (33)and Cγcalculated with Eq. (13)mainly result from the approximation of Eq. (33). Therefore, the errors in the Cγvalues of metals calculated with Eq. (13) can be estimated to be 5%.
It can be seen from Fig. 4 that the calculated f(Eph, hγ)values of Au agree well with experimental ones [20] at hγ = 8.1–11.6 eV, but not at hγ = 7.4–7.9 eV. It can also be seen from Fig. 3 and the calculated f(Eph, hγ) of Ni in Fig. 13 of Ref. [21], it is known that both the f(Eph, hγ) of Ni calculated in Ref.21 and the f(Eph,hγ)of Ni calculated with Eq. (21) are in good agreement at hγ = 9.2–11.6 eV but not at hγ = 7.6–8.6 eV. Thus, it can be concluded that Eq. (21) can be used to express the f(Eph, hγ) from Au at hγ = 8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV, and that Eq. (21) can be used to express the relative number of photo-emitted electrons with Ephin the cases that photons at hγ = 8.1–11.6 eV enter into Au and that photons at hγ = 9.2–11.6 eV enter into Ni. Therefore, from the relation between Eq. (21) and Eqs. (23)–(26), it can be concluded that Eqs. (23)–(26) can be used to express the relative values of Nelectrons2, Nreach2, Ndepth2, and Nenergy2from Au at hγ = 8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV.Then, from deducing Eqs. (27)–(29), it is determined that Eqs.(27)–(29)can be used to calculate the B,λ,and Emeanvalues of Au at hγ = 8.1–11.6 eV and Ni at hγ =9.2–11.6 eV. That is, the B, λ and Emeanvalues of Au at hγ = 8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV calculated from Eqs. (27)–(29) and shown in Tables 3 and 4 are correct.
The Cγvalues of Au calculated with Eqs. (2), (33), and(34),s = 11,NA,ρ,Aα,parameters(m%,n%,experimental AQE(hγ) [20] shown in Table 1 and parameters (B, λ)shown in Table 3 are shown in Table 3;the λγvalues of Au calculated with Eq. (2), s = 11, NA, ρ, Aα, Cγshown in Table 3 and n% shown in Table 1 are shown in Table 3.The Cγvalues of Ni calculated with Eqs. (2), (33), and(34),s = 10,NA,ρ,Aα,parameters(m%,n%,experimental AQE(hγ) [21]) shown in Table 2 and parameters (B, λ)shown in Table 4 are shown in Table 4;the λγvalues of Ni calculated with Eq. (2), s = 10, NA, ρ, Aα, Cγshown in Table 4 and n% shown in Table 2 are shown in Table 4.According to the conclusion that the B and λ values of Au at hγ = 8.1–11.5 eV shown in Table 3 and the B and λ of Ni at hγ = 9.2–11.6 eV shown in Table 4 are correct and the fact that Eq. (33)is correct,it is determined that the Cγvalues at hγ = 8.1–11.5 eV for Au shown in Table 3 and the Cγat hγ = 9.2–11.6 eV of Ni shown in Table 4, which are calculated with Eq. (33), are reasonable. From the estimation that errors in the Cγvalues of Au shown in Table 1 are about 5% and the comparison between Cγat hγ = 8.1–11.5 eV for Au shown in Table 3 and those in Table 1, it can be estimated that the errors in Cγat hγ =8.1–11.5 eV for Au calculated using Eq. (33) and shown in Table 3 are about 20%.Based on the estimation that the errors in Cγfor Ni shown in Table 2 are about 5%,and the comparison between Cγat hγ = 9.2–11.6 eV for Ni shown in Table 4 and those shown in Table 2,it can be estimated that the errors in Cγat hγ = 9.2–11.6 eV for Ni calculated using Eq. (33) and shown in Table 4 are about 30%.
It can be seen from Fig. 5 that the calculated f(Eph, hγ)values of Cu are in good agreement with experimental ones[25]at hγ = 7.7–11.6 eV,but not at hγ = 6.8 eV.Thus,it is concluded that Eq. (21) can be used to express the f(Eph,hγ) values from Cu at hγ = 7.7–11.6 eV. Therefore, from the relation between Eq. (21)and Eqs.(23)–(26),it can be concluded that Eqs. (23)–(26) can at least be used to express the relative values of Nelectrons2,Nreach2,Ndepth2,and Nenergy2from Cu at hγ = 7.7–11.6 eV. Then, from determining Eqs. (27)–(29), it can be concluded that Eqs. (27)–(29) can be used to calculate the B, λ, and Emeanvalues of Cu at hγ = 7.7–11.6 eV.That is,the B,λ,and Emeanvalues of Cu at hγ = 7.7–11.6 eV calculated using Eqs. (27)–(29)and shown in Table 5 are correct.
The Cγvalues of Cu calculated with Eqs. (2), (33), and(34),s = 11,NA,ρ,Aα,parameters(m%,n%,experimental AQE(hγ)[25],B,λ)are shown in Table 5.The λγvalue of Cu calculated with Eq. (2),s = 11,NA,ρ,Aα,Cγshown in Table 5 and n% shown in Table 5 are also shown in Table 5.From the conclusion that the B and λ values of Cu at hγ = 7.7–11.6 eV shown in Table 5 are correct and the fact that Eq. (33)is correct,it can be concluded that the Cγvalues at hγ = 7.7–11.6 eV of Cu calculated using Eq. (33)and shown in Table 5 are reasonable. There is no Cγat hγ = 7.7–11.6 eV for Cu calculated by other authors or using other current methods. Thus, we cannot estimate the errors in Cγat hγ = 7.7–11.6 eV for Cu calculated using Eq. (33). The relative differences among the Cγvalues at hγ <50 eV obtained by different authors can reach about 200% or more [19]. Thus, from the estimations that the errors in Cγat hγ = 8.1–11.5 eV for Au shown in Table 3 are about 20%, and that the errors in Cγat hγ = 9.2–11.6 eV for Ni shown in Table 4 are about 30%, it can be concluded that the method of calculating Cγfor metals using Eq. (33) is more accurate. According to the estimation that the errors in Cγfor metals calculated using Eq. (13)are about 5%,it can be concluded that the method of calculating Cγfor metals using Eq. (13)is very accurate.From the perspective of accuracy of the calculated Cγ, it appears that the method of calculating Cγwith Eq. (13)presented in the first SEE model is better than that of calculating Cγwith Eq. (33) presented in the second SEE model.However,it is important to note that in the case that the absolute g(Ephhγ) is not known, the method of calculating the Cγvalue for metals using Eq. (13)cannot be used to calculate Cγ,but the method of calculating the Cγvalue for metals using Eq. (33) can be used to calculate Cγ. For example,because only the relative g(Ephhγ)value of Cu is known in this study[25],the Cγvalue at hγ = 7.7–11.6 eV for Cu can only be calculated using the method of calculating the Cγvalue for metals with Eq. (33). It is also important to note that in the cases that AQE(hγ) are not known, the first SEE model cannot be used to calculate f(Eph, hγ), B, λ, and Emean, but the second SEE model can be used to do so.
From the comparison between Fig. 2 and Fig. 4 and the comparison between the f(Eph, hγ) values of Ni calculated with Eq. (10) and those calculated with Eq. (21) in Fig. 3,it is known that the differences between f(Eph, hγ) values for Au and Ni calculated with Eq. (10)and those calculated with Eq. (21) are very small. From Tables 1, 2, 3, 4, it is seen that the B,λ,and Emeanvalues of Au and Ni calculated with Eqs. (17)–(19) are approximately equal to those calculated with Eqs.(27)–(29).That is,Eqs.(9)and(17)–(19)deduced in the first SEE model can be replaced with Eqs.(20)and(27)–(29)deduced in the second SEE model,respectively, and vice versa. From the above comparison among f(Eph, hγ), B, λ, and Emeanfor Au and Ni, and the courses of calculating f(Eph, hγ), B, λ, and Emeanfor Au,Cu, and Ni, we found that the values of Cγhave little influence on the shape of f(Eph, hγ) and the values of B, λ,and Emean, but that both g(Ephhγ) and hγ significantly influence them. For example, the shape of g(Ephhγ) significantly influences the shape of f(Eph, hγ).
The excited electrons with Evac<1.0 eV lose energy mainlybymultipleelectron–phononscattering[13, 37, 45, 46]. Electron–phonon scattering loses less energy every time there is scattering, and the excited electrons with Evac<1.0 eV may still become emitted electrons after several occurrences of electron–phonon scattering [13, 37, 45, 46]. Thus, if the excited electrons with Evac<1.0 eV have more energy, they can travel a greater distance to escape into vacuum. Therefore, the mean escape depth of the excited electrons with Evac-<1.0 eV is proportional to Evac[13,37,45,46].However,the excited electrons with Evacvalues that are much larger than 1.0 eV lose energy mainly by single electron–electron scattering.Electron–electron scattering results in the loss of a larger amount energy at every scattering,and the excited electrons with Evacvalues much larger than 1.0 eV almost cannot become emitted electrons after single electron–electron scattering[13,37,45,46].The probability that an excited electron with Evacmuch larger than 1.0 eV undergoes single electron–electron scattering per unit path length of excited electron is proportional to Evac[13,37,45,46].Thus,the mean escape depth of the excited electrons with Evacmuch larger than 1.0 eV is inversely proportional to Evac.Most secondary electrons have energy Evac>1.0 eV [32, 33], and Eamis much larger than 1.0 eV,and the secondary electrons lose energy mainly by single electron–electron scattering. Thus, λsis inversely proportional to Evac, and the mean escape depth of secondary electrons with E0(0E0ΦEF1.5EF) can be expressed as Eq. (5).In other words,Eq. (5)is correct in the case that the Eamis much larger than 1.0 eV. Therefore, from the fact that Eq. (6) is derived from Eq. (5), it can be concluded that Eq. (6)is correct in the case that Emeanis much larger than 1.0 eV. Then, it is concluded that Eqs. (10),(17)–(19),(21),and(27)–(29)derived from Eq. (6)are also correct in the case that Emeanis much larger than 1.0 eV.From Tables 1,2,3,4,5,it can be seen that the Emeanof Au at hγ = 8.1–11.5 eV, Ni at hγ = 9.2–11.6 eV and Cu at hγ = 7.7–11.6 eV are much larger than 1.0 eV. For this reason, f(Eph, hγ) calculated here for Au at hγ = 8.1–11.6 eV, Ni at hγ = 9.2–11.6 eV, and Cu at hγ = 7.7–11.6 eV are in good agreement with the corresponding experimental ones and the ones calculated by other authors [20, 21, 25],and the B, λ, and Cγvalues calculated here for Au at hγ = 8.1–11.5 eV, Ni at hγ = 9.2–11.6 eV and Cu at hγ =7.7–11.6 eV are correct.
If the metal surfaces are contaminated or if metals have some impurities, the photo-emission from these metals becomes more complex. Thus, it is important to note that we must use experimental f(Eph,hγ)and AQE(hγ)values of clean and pure metals to investigate the corresponding f(Eph, hγ), Emean, B, λ and Cγin this work, and that the experimental f(Eph, hγ) and AQE(hγ) used in this work are those of three clean and pure metals [20, 21, 25]. In other words,the two SEE models presented in this work are only suitable for photo-emission from clean and pure metals in the vacuum ultraviolet.
6 Conclusion
In this study, Eqs. (10) and (21) for f(Eph, hγ) from metals have been deduced and proven to be correct for the cases of Au at hγ = 8.1–11.6 eV and Ni at hγ = 9.2–11.6 eV, respectively. Thus, from the relation between Eq. (10)and Eqs.(12)–(16)as well as the relation between Eq. (21)and Eqs. (23)–(26), it is concluded that Eqs. (12)–(16) can at least be used to express the corresponding relative values of Nelectrons, AQE(hγ), Nreach, Ndepthand Nenergy, respectively; and that Eqs. (23)–(26) can be used to express the corresponding relative values of Nelectrons2, Nreach2, Ndepth2and Nenergy2, respectively. Therefore, from determining Eqs. (17)–(19) and (27)–(29), it can be concluded that Eqs. (17)–(19) and Eqs.(27)–(29) can be used to calculate the B, λ, and Emeanvalues for Au at hγ = 8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV.
The AQE(hγ)value from Au at hγ = 7.4–11.5 eV and Ni at hγ = 7.6–11.6 eV is calculated using Eqs. (2), (33), and(34), the B and λ values for Au and Ni calculated with Eqs.(17)–(18),and the Cγvalues for Au and Ni calculated using Eq. (13). These calculated AQE(hγ) values from Au and Ni agree well with the corresponding experimental ones.Thus,from the conclusions that the B and λ values of Au at hγ = 8.1–11.5 eV and Ni at hγ = 7.6–11.6 eV calculated with Eqs. (17)–(18) are correct and the conclusion that Eq. (33) is correct, it can be concluded that the Cγvalues of Au at hγ = 8.1–11.5 eV and Ni at hγ =7.6–11.6 eV calculated with Eq. (13) are correct. Therefore,from the conclusions that Eq. (13)can at least be used to express the relative values of AQE(hγ) from Au at hγ = 8.1–11.5 eV and Ni at hγ = 7.6–11.6 eV, it can be concluded that Eq. (13)can be used to express the absolute values of AQE(hγ)from Au at hγ = 8.1–11.5 eV and Ni at hγ = 7.6–11.6 eV.
The Cγvalues of Au are calculated using Eqs.(2),(33),and (34), s = 11, NA, ρ, Aα, parameters (m%, n%, experimental AQE(hγ)) shown in Table 1 and parameters (B, λ)shown in Table 3, the Cγof Ni values are calculated using Eqs.(2),(33),and(34),s = 10,NA,ρ,Aα,parameters(m%,n%, experimental AQE(hγ)) shown in Table 2 and parameters(B,λ)shown in Table 4.According to the conclusion that the B and λ values for Au at hγ = 8.1–11.5 eV shown in Table 3 and the B and λ values for Ni at hγ =9.2–11.6 eV shown in Table 4 are correct and the fact that Eq. (33) is correct, it can be concluded that the Cγvalues for Au at hγ = 8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV calculated using Eq. (33) are reasonable. From the comparison between the Cγvalues for Au at hγ = 8.1–11.5 eV for Au calculated with Eq. (33)and the corresponding ones shown in Table 1, it can be estimated that the errors in the Cγat hγ = 8.1–11.5 eV for Au calculated with Eq. (33)are about 20%. Based on the comparison between the Cγvalues for Ni at hγ = 9.2–11.6 eV for Ni calculated with Eq. (33) and corresponding ones shown in Table 2, it can be estimated that the errors in Cγat hγ = 9.2–11.6 eV for Ni calculated with Eq. (33) are about 30%.
Equation (21) for the f(Eph, hγ) at hγ = 7.7–11.6 eV of Cu has been experimentally proven.Thus,from the relation between Eq. (20) and Eqs. (23)–(26), it is concluded that Eqs. (23)–(26) can be used to calculate the relative values of Nelectrons2, Nreach2, Ndepth2, and Nenergy2from Cu at hγ = 7.7–11.6 eV. Therefore, from determining Eqs. (27)–(29),it can be concluded that Eqs.(27)–(29)can be used to calculate B, λ, and Emeanvalues for Cu at hγ = 7.7–11.6 eV.
The Cγvalues for Cu are calculated using Eqs.(2),(33),and (34), s = 11, NA, ρ, Aα, parameters (m%, n%, experimental AQE(hγ))shown in Table 5,B and λ calculated with Eqs.(27)–(28).From the conclusion that the B and λ values for Cu at hγ = 7.7–11.6 eV calculated with Eqs. (27)–(28)are correct and the fact that Eq. (33) is correct, it can be concluded that the Cγvalues at hγ = 7.7–11.6 eV for Cu calculated using Eq. (33) are reasonable. The relative differences among the Cγvalues at hγ <50 eV obtained by different authors can reach about 200%or more[19].Thus,from the estimations that the errors in Cγfor Au at hγ =8.1–11.5 eV and Ni at hγ = 9.2–11.6 eV calculated using Eq. (33) are about 20% and 30%, it can be concluded that the method of calculating Cγfor metals using Eq. (33) is more accurate.From the estimation that the errors in Cγfor metals calculated using Eq. (13) are about 5%, it can be concluded that the method of calculating Cγfor metals using Eq. (13) is very accurate.
Author contributions All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Ai-Gen Xie,Yi-Fan Liu and Hong-Jie Dong.The first draft of the manuscript was written by Ai-Gen Xie and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
 Nuclear Science and Techniques2022年8期
Nuclear Science and Techniques2022年8期
- Nuclear Science and Techniques的其它文章
- Transient analysis and optimization of passive residual heat removal heat exchanger in advanced nuclear power plant
- Recent progress in two-proton radioactivity
- Selection diagram of design algorithms for neutron-focusing supermirrors
- Flow field effect of delayed neutron precursors in liquid-fueled molten salt reactors
- A high fidelity general purpose 3-D Monte Carlo particle transport program JMCT3.0
- New flexible CsPbBr3-based scintillator for X-ray tomography
