Selection diagram of design algorithms for neutron-focusing supermirrors
Wen-Bo Mo· Hua-Rui Wu· Xue-Wu Wang
Abstract The neutron supermirror is an important neutron optical device that can significantly improve the efficiency of neutron transport in neutron guides and has been widely used in research neutron sources. Three types of algorithms, including approximately ten algorithms, have been developed for designing high-efficiency supermirror structures.In addition to its applications in neutron guides,in recent years,the use of neutron supermirrors in neutronfocusing mirrors has been proposed to advance the development of neutron scattering and neutron imaging instruments,especially those at compact neutron sources. In this new application scenario, the performance of supermirrors strongly affects the instrument performance; therefore, a careful evaluation of the design algorithms is needed. In this study,we examine two issues:the effect of nonuniform film thickness distribution on a curved substrate and the effect of the specific neutron intensity distribution on the performance of neutron supermirrors designed using existing algorithms. The effect of film thickness nonuniformity is found to be relatively insignificant, whereas the effect of the neutron intensity distribution over Q (where Q is the magnitude of the scattering vector of incident neutrons)is considerable.Selection diagrams that show the best design algorithm under different conditions are obtained from these results.When the intensity distribution is not considered, empirical algorithms can obtain the highest average reflectivity, whereas discrete algorithms perform best when the intensity distribution is taken into account. The reasons for the differences in performance between algorithms are also discussed. These findings provide a reference for selecting design algorithms for supermirrors for use in neutron optical devices with unique geometries and can be very helpful for improving the performance of focusing supermirror-based instruments.
Keywords Neutron-focusing supermirror · Design algorithm·Thickness nonuniformity·Intensity distribution over Q · Selection diagram
1 Introduction
Neutron beams are recognized as an essential probe in a wide range of scientific and industrial applications [1–7].Many dedicated neutron scattering and neutron imaging instruments have been built in reactor-based neutron sources and modern spallation neutron sources.In addition to these large-scale sources, compact accelerator-driven neutron sources (CANS) have received much attention in recent years for their advantages of low cost and flexibility[8]. Many CANS projects have been launched to meet increasing demands for neutron beams in multiple disciplines [9, 10]. These demands have also stimulated the development of accelerators for compact neutron sources,and various new design schemes are continuously being proposed [11, 12]. However, the low neutron intensity of CANS is a challenging issue for attempts to provide competitive neutron scattering and imaging measurements.Great efforts have been made to enhance the available neutron intensity, including building more powerful accelerators and targets and developing highly efficient neutron optical devices.
One of the most promising approaches is grazing incidence optics, which typically uses curved confocal conic section mirrors to focus neutron beams. These mirrors are well able to enhance the neutron intensity for neutron scattering [13–20] and imaging [21–23] instruments. In China,a small-angle neutron scattering instrument is under construction at the Compact Pulsed Hadron Source(CPHS); it is based on a nested neutron-focusing supermirror assembly and is expected to improve the neutron intensity at the sample by nearly 100 times compared with that of pinhole collimation [17–20]. To enable higher reflectivity and a larger collecting area, it is essential to deposit neutron supermirror coatings on the surface of the focusing mirrors.
The neutron supermirror is a multilayer structure composed of thin layers of two materials(usually Ni/Ti or NiC/Ti) stacked successively according to a specific thickness sequence [24, 25]. It can increase the critical angle of neutron total reflection by a factor of m compared with that of pure nickel. The critical reflectivity and m value are the most important performance metrics of neutron supermirrors. They largely determine the transport or focusing efficiency, which are the primary concern in the design of multilayer structures.
To pursue high-performance supermirrors, various design algorithms have been developed. They can be roughly divided into three categories:continuous,discrete,and empirical algorithms [26–28]. Continuous algorithms typically solve a differential equation for dD/dn, where D n( )is the thickness of the nth bilayer[24,25,29–31].The discrete algorithm was first proposed by Hayter and Mook in 1989 [26]. This type of algorithm considers the discrete nature of the multilayer structure of supermirrors[26, 28, 32, 33]. Empirical algorithms are generalizations of continuous algorithms in which parameters with no a priori physical relationship are added, and optimization is performed by traversing the parameter space [27, 34–36].
Since their invention in 1976,neutron supermirrors have been widely used in neutron guides to transport beams at almost all research neutron sources.These algorithms have been successfully applied to the design of supermirrors for neutron guides and have greatly facilitated the use of neutrons in many applications. However, several practical issues in the design of focusing supermirrors require a careful evaluation and comparison of existing design algorithms. First, the curved geometry of the mirrors may result in more severe thickness deviations in the layers of supermirrors (see Sect. 2.2); thus, the sensitivity of the design algorithms to thickness deviations should be examined. Second, the use of focusing supermirrors in CANS provides an additional opportunity to optimize the supermirror structure for higher neutron intensity. The reflectivity of supermirrors depends on Q, the quantity of neutron wavevector transfer in the reflection process;incident neutron intensity also has a distribution over Q because of the neutron wavelength distribution of the source and variation in the grazing incidence angles of neutrons on the mirrors (as described in Sect. 2.3). This feature, which is often ignored in the application of supermirrors in neutron guides, may result in a preference for certain design algorithms and may be very important for further improvement in the focusing efficiency of neutron-focusing mirrors.
In this study, we first describe the design parameters of the three algorithms used for comparison and then introduce a model for calculating the film thickness distribution during the coating of curved surfaces.We also describe the calculation of the neutron intensity distribution over Q of a typical thermal neutron source. A schematic diagram is shown in Fig. 1. Then, we compare the reflectivity performance of the three types of algorithms, considering the nonuniform film thickness distribution of a supermirror coated on a curved substrate and the distribution of neutron intensity over Q. The results are shown in the form of selection diagrams that indicate the optimal algorithm under various design conditions. The reasons for the differences in performance between the three algorithms are discussed in detail. In the last section, we summarize the findings and provide suggestions for selecting design algorithms for supermirrors for use in neutron-focusing mirrors.
2 Methods
2.1 Parameter selection of algorithms for supermirror design
To evaluate and compare the three types of algorithms described above,we choose a typical representative of each type: the Gukasov–Ruban–Bedrizova (GRB) algorithm[29, 30] for the continuous type, the Masalovich (Mas)algorithm[33]for the discrete type,and the ABC algorithm[27, 36] for the empirical type. These algorithms exhibit the main characteristics of their types and thus are suitable for demonstrating their performance in different design parameter spaces.
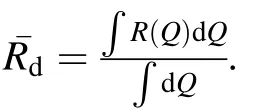

Fig. 1 (Color online)Schematic view of a nonuniform layer thickness distribution on a curved surface and b focusing of neutron beams from a source to a detector by reflective mirrors

Fig.2 (Color online)Average reflectivity of the three algorithms as a function of m under the initial conditions.The difference between the three algorithms is controlled within 0.001
2.2 Film thickness distribution on curved surface coating
We employed the model proposed by Bishop et al. [37]to calculate the thickness distribution of sputtered films on curved substrates. This model is based on the characteristics of a magnetron sputtering system with a rotating substrate, as shown in Fig. 3. The ejected mass flux decreases in proportion to the inverse square of the distance it travels to the substrate. Therefore, it can also be used to describe coating systems with similar spatial structures, such as ion beam sputtering. In addition, the substrate rotates at a variable speed around an external center [19](as indicated by‘‘Revolution’’in Fig. 3)so that the nonuniformity of the axial thickness distribution of the film can be ignored, and only the nonuniformity of the azimuthal thickness distribution must be considered.

Fig. 3 (Color online) Schematic diagram of sputtering chamber geometry. Curved gray arrow indicates substrate rotation during deposition
Note that various methods have been proposed to reduce the thickness nonuniformity of coatings on curved surfaces,such as the use of shadow masks or differential deposition techniques [19, 38–43]. However, their implementation is complicated because they require customized designs for different sputtering configurations and substrates. Therefore, it is necessary to evaluate the effect of thickness nonuniformity on the supermirror reflectivity to determine whether these additional steps are needed.
In this model, we considered a cylindrical concave curved substrate (i.e., one with curvature in the azimuthal direction and not in the axial direction).The side length of the surface is expressed as a dimensionless number, which is the ratio of the side length to the target–substrate distance. Thus, the main parameter affecting the thickness distribution is the radius of curvature (ROC) of the substrate. Figure 4 shows the relative thickness distribution of a layer deposited on substrates with ROCs of 50, 80, and 160 mm.
To simplify the calculation,we assume that each layer in the supermirror has the same relative thickness distribution.As a result, the position of a point whose thickness is normalized to the value 1 will yield different absolute thickness distributions. Therefore, the position of this normalization point is also a parameter of the reflectivity.As shown in Fig. 5, the abscissa is the azimuthal position of the normalization point.Taking m=5 and a ROC of 80 mm as an example,we calculate the average reflectivity ¯Rdof the supermirror designed by the three algorithms for this series of thickness distributions. The optimal value occurs when the normalization point is located at the position where the azimuthal angle is equal to 9.6°. The film thickness distribution model described here will be employed to compare the three algorithms.

Fig. 4 (Color online) Relative thickness distribution of a layer deposited on substrates with ROCs of 50, 80, and 160 mm
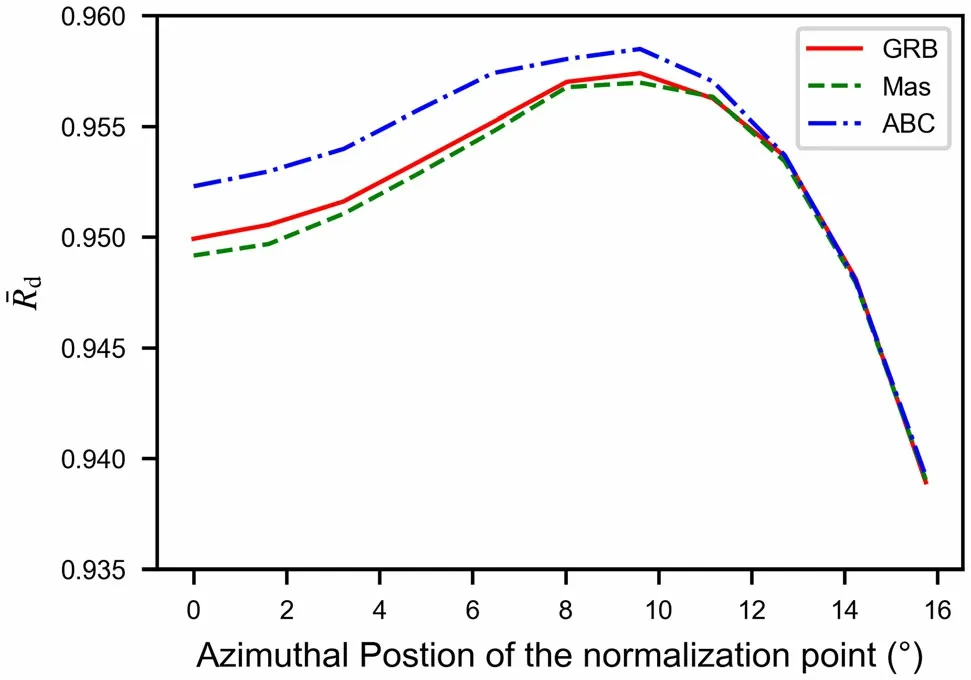
Fig.5 (Color online)Variation of average reflectivity of supermirror(m=5) versus position of layer thickness normalization point
2.3 Distribution of neutron intensity with respect to Q
As noted above, the use of neutron-focusing mirrors introduces a neutron intensity distribution with respect to Q, which originates from the grazing angle distribution of incident neutrons on mirrors.Here,we use a simple model to formulate this intensity distribution,as shown in Fig. 1b.The neutron-focusing mirror has a nested structure [17]consisting of a series of concentric conical mirrors with different radii. Assuming a point neutron source, the angular distribution of neutrons grazing the surface of a mirror with radius R should be proportional to the solid angle, which is given by

where A is the reflective area of the focusing mirror, and L is the horizontal distance between the center of the focusing mirror and the neutron source.
To simplify the calculation,we assume that the length of the focusing mirror, w, is short enough that the neutron grazing incidence angle of the mirror with the same radius can be regarded as having the same value,and mirrors with different radii will not block each other.Thus,the effective reflective area is

where
Therefore, the angular distribution is
The wavelengths of incident neutrons follow the Maxwellian distribution, which peaks around the thermal wavelength at the moderator temperature T. The neutron flux φ(λ ), with the unit of neutron counts per second per unit wavelength, is thus expressed as

Figure 6 shows the angular distribution p(θ), neutron flux φ(λ ),and I(Q).As shown in Fig. 6a,the proportion of incident neutrons collected by the mirror increases with increasing θ. The neutron flux decreases rapidly with increasing wavelength,as shown in Fig. 6b.Over the range of angles and wavelengths we consider, the angular distribution changes only by a factor of 2,whereas the neutron flux intensity changes by several orders of magnitude.Therefore, I(Q) follows the trend of φ(λ ) and increases rapidly with increasing Q, as shown in Fig. 6c. Note that the Q-dependent neutron intensity also depends on the size of the mirrors. Because larger mirrors can reflect more neutrons at larger grazing incidence angles, the proportion of high-Q neutrons in the neutron intensity distribution increases.

Fig.6 (Color online)a Angular distribution,b neutron flux φ(λ ),and c I(Q). The parameters used in the calculation are R1 =8 cm,R2 =12 cm, L=4 m, and λT =2 ˚A
3 Results and discussion
3.1 Effect of film thickness nonuniformity on the average reflectivity of supermirrors without considering I(Q)
First, we compared the average reflectivity obtained by the three algorithms for various m values and film thickness nonuniformities.Here,the average reflectivity is defined as

The thickness deviation Δd, which is defined as the difference between the thickest and thinnest positions, is used to quantify the nonuniformity of the film thickness.Figure 7a shows the algorithm with the highest average reflectivity for each point (m,Δd) in the parameter space.
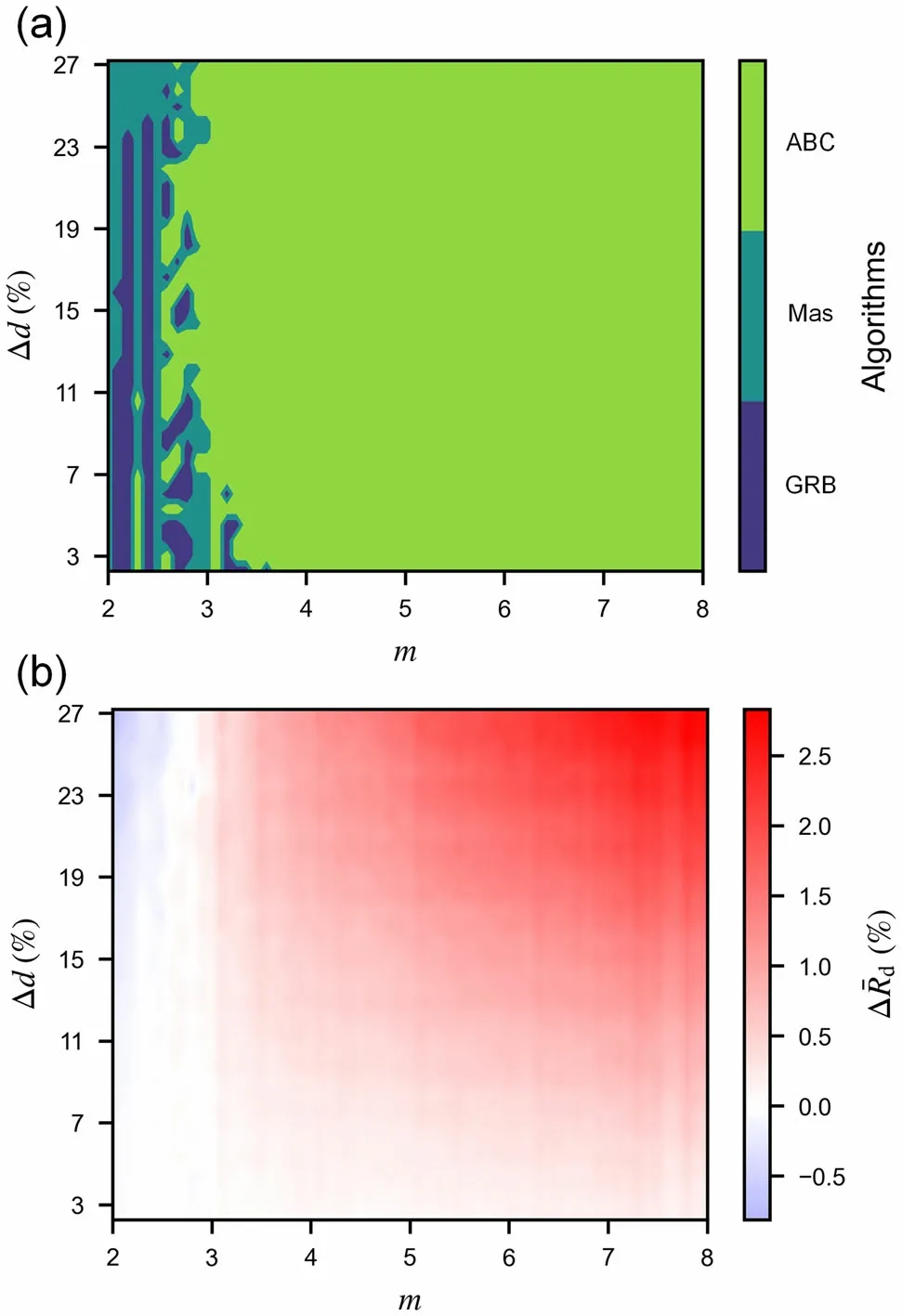
Fig. 7 (Color online) a Algorithms with highest average reflectivity for various m and film thickness nonuniformity Δd. b Differences between average reflectivity of the ABC algorithm and those of the other two algorithms
In Fig. 7a, an obvious dividing line appears near m=2.8. When m<2.8, the average reflectivity of the GRB and Mas algorithms is higher, whereas when m >2.8, the ABC algorithm obtains the highest average reflectivity. To better show the advantages of the ABC algorithm over the other two algorithms,Fig. 7b shows the differences between the average reflectivity of the ABC algorithm and those of the other two algorithms at each parameter point,where Δ¯Rd=(¯Rd,ABC- ¯Rd,others)/¯Rd,others.This result indicates that the ABC algorithm can better handle large m values and high film thickness nonuniformity. For m=8 and a film thickness nonuniformity Δd >25%,its average reflectivity can be 2.8%higher than those of the other two algorithms.
We further explored the origins of the observed differences between the three algorithms.Consider a supermirror with m=5 as an example. Figure 8 shows the reflectivity curves of the three algorithms, where the solid line is the original reflectivity curve, and the dotted line is the reflectivity curve considering the effect of film thickness nonuniformity (Δd =8.6%). The reflectivity curve of the ABC algorithm differs from the other two. For the ABC algorithm, the reflectivity decreases continuously with increasing Q, and the degradation is more severe. By contrast, for both the GRB and Mas algorithms, the reflectivity first decreases with increasing Q and then remains stable at an almost constant value, as indicated by the high-Q plateau in the reflectivity curves.Consequently,the variation in average reflectivity with film thickness is different for the three algorithms. We selected the layers contributing to the neutron reflectivity at Q/Qc=3 ~4 and calculated the corresponding reflectivities,as shown in Fig. 9. When the film thickness decreases, the reflectivity curve shifts toward higher Q. For the GRB and Mas algorithms, the slope of the fitting line is very close to 0(approximately - 0.005), regardless of whether the film thickness inhomogeneity is considered. The intercept difference is approximately 0.035 and is the source of the average reflectivity difference when the film thickness nonuniformity is considered. However, the reflectivity curve of the ABC algorithm has a noticeable slope (-0.035), and the slope also increases (to - 0.055) when the film thickness nonuniformity is considered. Therefore, the decrease in reflectivity is only approximately 0.01,which is smaller than that of the GRB and Mas algorithms.
Fig. 8 (Color online) Reflectivity curves of the three algorithms (m=5)

Fig. 9 (Color online) Reflectivity curves of the three algorithms (m=5) at Q/Qc =3 ~4. Straight lines are linear fits of the plateaus
3.2 Effect of film thickness nonuniformity on weighted average reflectivity of supermirrors considering I(Q)
As demonstrated above, the reflectivity of each algorithm is distributed with respect to Q, and the intensity of incident neutrons also has a distribution with respect to Q. This result suggests decoupling between the optimal supermirror structure and the geometry of the focusing mirrors and source,which can be employed to optimize the design parameters and select the best design algorithm.Therefore, in this section, we incorporate the effect of geometric factors into the evaluations to explore the influence of film thickness nonuniformity.
Considering the neutron intensity distribution over Q,we compared the average reflectivity obtained by the three algorithms under various values of m and the film thickness nonuniformity. This comparison involves the characteristics of neutron sources,which can more accurately indicate the performance of supermirrors in practical applications.Instead of the average reflectivity written as Eq. (10) in Sect. 3.1, here the average reflectivity weighted by the neutron intensity distribution over Q is used.It is defined as
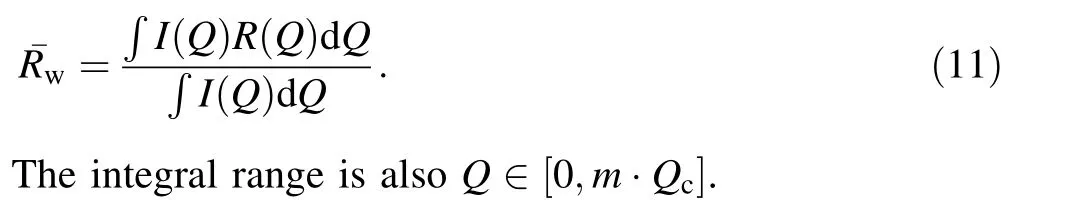
The same range of m and film thickness nonuniformity is used to compare the three algorithms. Figure 10a shows the algorithm with the highest weighted average reflectivity for each point (m,Δd) in the parameter space.

Fig. 10 (Color online) a Algorithms with highest weighted average reflectivity for various values of m and film thickness nonuniformity Δd. b Difference between weighted average reflectivity of the Mas algorithm and ABC algorithm
When the neutron intensity distribution over Q is considered, the selection diagram changes completely. The ABC algorithm performs well for small m and high film thickness nonuniformity. When m >4.5, the Mas algorithm yields the highest weighted average reflectivity.Figure 10b shows the difference between the weighted average reflectivities of the Mas and ABC algorithms at eachparameterpoint,where Δ¯Rw=(¯Rw,Mas- ¯Rw,ABC)/¯Rw,ABC. This comparison indicates that the Mas algorithm has more advantages at large m and low film thickness nonuniformity. For m=8 and Δd<15%, its weighted average reflectivity is 4.1% higher than that of the ABC algorithm.
This difference can still be attributed to the difference in the reflectivity curves of the three algorithms. Figure 11 shows the reflectivity curves for nonuniform film thickness(Δd =8.6%). Because there is a plateau in the reflectivity curves of the Mas and GRB algorithms, their reflectivity for high-Q incident neutrons is higher than that of the ABC algorithm. According to the neutron intensity versus Q curve in Fig. 6c, the neutron intensity is higher for high Q, which results in a higher weighted average reflectivity.
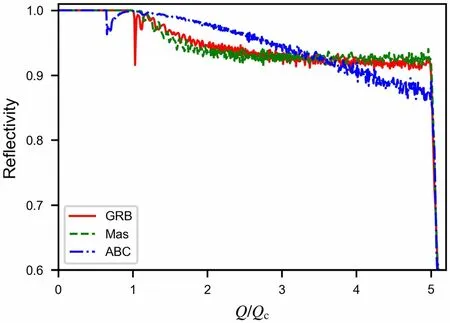
Fig.11 (Color online)Reflectivity curves of the three algorithms at a film thickness nonuniformity of 8.6%

Fig.12 (Color online)Effects of a film thickness nonuniformity and b neutron intensity distribution over Q on average reflectivity of the ABC algorithm
We also compared the effects of film thickness nonuniformity and neutron intensity distribution over Q on the average reflectivity of the ABC algorithm. Figure 12a shows the average reflectivity difference between films of nonuniform and uniform thickness. Figure 12b reveals difference between weighted average reflectivity with and without considering the neutron intensity distribution over Q. Even for m=8, the degradation of the reflectivity at a nonuniformity of 10% is less than 3%, which is much smaller than the effect of the Q-dependent neutron intensity distribution. The film thickness nonuniformity affects the reflectivity to the same degree as the Q distribution only at small m (m<3) and especially large film thickness nonuniformity(Δd >25%).This result demonstrates that it is worth considering the characteristics of neutron sources in the commonly used design parameter space of supermirrors.
3.3 Origins of differences in reflectivity
As shown in Sects. 3.1 and 3.2, the reflectivity curves of supermirrors generated by the three algorithms are different. In this section, we try to explain the reasons for these differences.
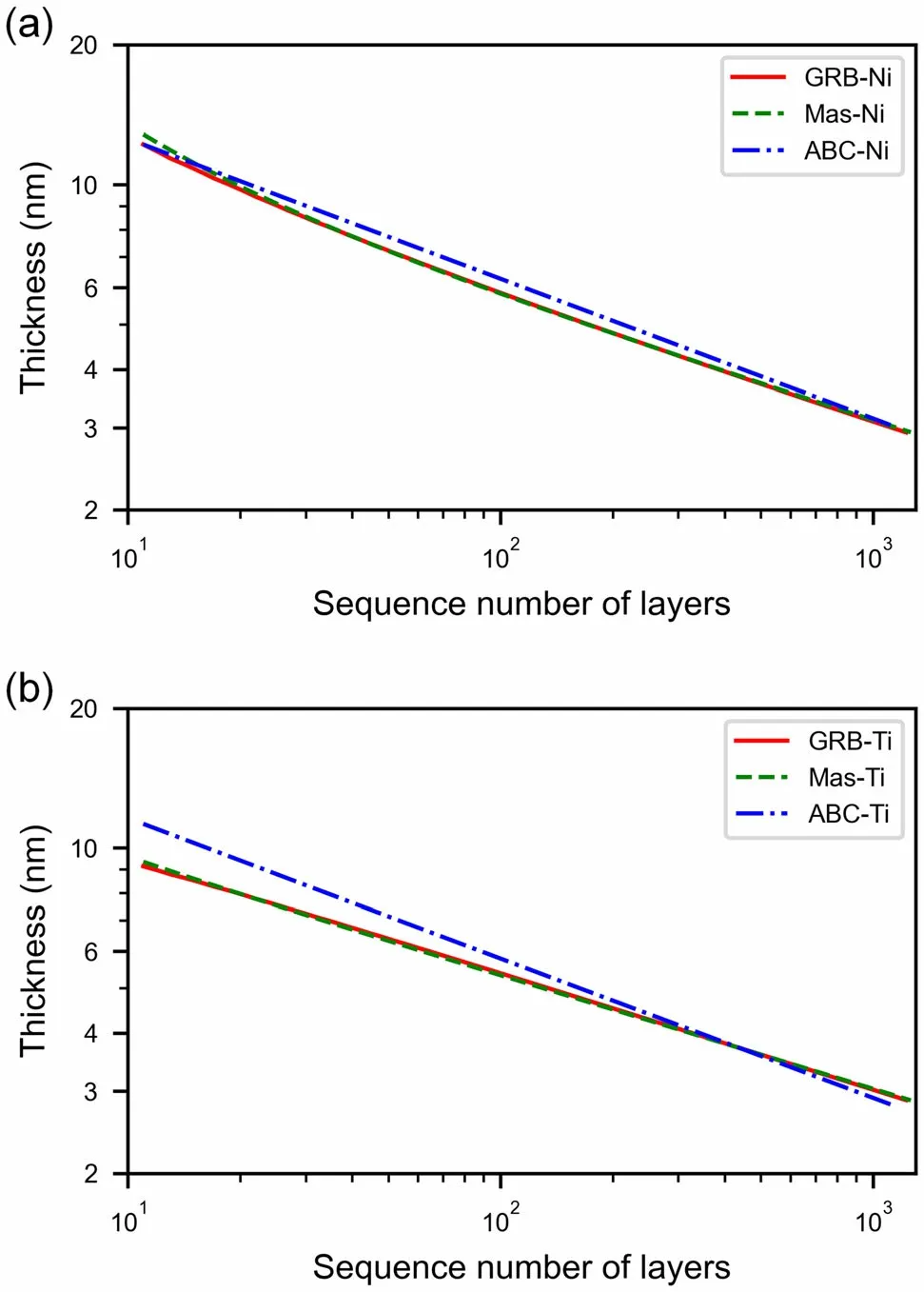
Fig. 13 (Color online) Thickness distribution of each layer in supermirror multilayer sequence
The reflectivity differences are essentially attributable to differences in the supermirror multilayer sequence,including layer thickness and layer number distribution.Figure 13 shows the thickness distribution of each layer in the sequences designed by the three algorithms. As the ordinal number increases, the position of a layer in the multilayer sequence becomes closer to the substrate.Because the first 10 layers contribute to the reflectivity at Q/Qc<1, where there is no difference in the output of the algorithms, we compare only the structures of other layers here. As shown in Fig. 13, the layer thicknesses in the multilayer sequences designed by the GRB and Mas algorithm are very similar, but the layer thickness of the multilayer sequence designed by the ABC algorithm is relatively large. According to the principle of Bragg diffraction,

where dnis the thickness of the nth layer; Qnis the Q of neutrons satisfying the corresponding Bragg conditions,and the layer has high reflectivity to these neutrons.Therefore, because of the relatively thick layer, the ABC algorithm can yield higher reflectivity for low-Q neutrons.
From another perspective,the curves in Fig. 13 can also be interpreted as indicating that layers with the same thickness as the other two algorithms appear later in the multilayer structure designed by the ABC algorithm.Thus,the ABC algorithm allocates more layers to the low-Q regime.Figure 14a shows the distribution of the number of bilayers over Q for the three algorithms, which confirms this interpretation.For intuitive understanding,in Fig. 14b,we divide the reflectivity curve into four Q ranges(0<Q/Qc≤2,2<Q/Qc≤3,3<Q/Qc≤4,4<Q/Qc≤5), and compare the number of bilayers that each algorithm allocates to each Q range. The ABC algorithm assigns more layers to the low-Q regime; thus, it obtains higher reflectivity for low-Q neutrons.By contrast,the GRB and Mas algorithms allocate more layers to the high-Q regime, resulting in higher reflectivity for high-Q neutrons.
In essence, these differences originate from the theoretical basis of these algorithms, which has also been discussed in [44]. The continuous and empirical algorithms were derived from the kinematic theory of neutron scattering, which considers only the Born approximation.These results are valid only for the maximum reflectivity,Rmax≪1, which requires that the number of nth bilayers,Nn, is much greater than 1. By contrast, the dynamical theory of neutron diffraction considers multiple scattering events and the associated extinction effects, which are more pertinent for supermirrors.The solutions of the exact dynamical theory of reflection are used in discrete algorithms.It may be surprising that the performance of the GRB algorithm is very similar to that of the discrete algorithm. The reason is that in contrast to the Mezei algorithm[24,25]and the original GRB algorithm[29],the improved GRB algorithm [30] and Schelten–Mika (SM)algorithm [31] introduced a refraction correction for finding the thickness of layers in a supermirror design. Thus,their thickness distribution function no longer has a powerlaw form, as shown in Fig. 13a.

Fig. 14 (Color online) a Distribution of number of bilayers over Q and b number of bilayers allocated to each interval in multilayer sequence of each algorithm
4 Conclusion
In this study, we considered the effect of the nonuniformity of the film thickness on the reflectivity of a supermirror coated on a curved substrate. The GRB, Mas,and ABC algorithms were compared, and the results were presented as a selection diagram. When the distribution of neutron intensity with respect to Q is not considered, the ABC algorithm obtains the highest average reflectivity.However, when the average reflectivity weighted by the neutron intensity distribution over Q is considered,the Mas algorithm performs best. This difference arises from the different strategies for allocating layer thickness and the number of bilayers in the designed multilayer sequences of each algorithms. Empirical algorithms, represented by the ABC algorithm, tend to allocate more and thicker bilayers in the low-Q regime,which results in higher reflectivity of low-Q neutrons. By contrast, the continuous and discrete algorithms assign more bilayers in the high-Q regime,resulting in higher neutron reflectivity of high-Q neutrons.This result indicates that it would be very helpful to include the characteristics of neutron sources when optimizing the supermirror structure, which can further improve the performance of neutron-focusing mirrors. In addition, it was confirmed that the nonuniformity of the film thickness has a minor effect on the reflectivity of supermirrors. By applying an appropriate algorithm, its effect can be wellsuppressed without taking additional measures in the coating process (e.g., using shadow masks or differential deposition). These findings provide a reference for the selection of design algorithms for supermirrors for use in neutron-focusing mirrors and can be helpful for improving the performance of supermirror-based focusing instruments.
Author contributions All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by Wen-Bo Mo, Hua-Rui Wu, and Xue-Wu Wang.The first draft of the manuscript was written by Wen-Bo Mo, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
 Nuclear Science and Techniques2022年8期
Nuclear Science and Techniques2022年8期
- Nuclear Science and Techniques的其它文章
- Transient analysis and optimization of passive residual heat removal heat exchanger in advanced nuclear power plant
- Recent progress in two-proton radioactivity
- Flow field effect of delayed neutron precursors in liquid-fueled molten salt reactors
- A high fidelity general purpose 3-D Monte Carlo particle transport program JMCT3.0
- New flexible CsPbBr3-based scintillator for X-ray tomography
- Correction to: Shortening the delivery time of proton therapy by real-time compensation method with raster scanning
