基于改进IAHP-VIKOR 方法的雷达装备维修性评估*

张馨予，胡 冰，姜玉博

（1.空军预警学院，武汉 430019；2.解放军63656 部队，新疆 和硕 841200；3.解放军93656 部队，北京 101100）

0 引言

雷达装备维修性是指雷达装备在规定的条件下和规定的时间内，按规定的程序和方法进行维修时，保持或恢复其规定状态的能力。雷达装备维修性评估是在雷达装备寿命周期各阶段，对其维修是否方便、快捷、经济，是否满足维修性指标要求做出的评价。在雷达装备鉴定定型阶段对其维修性进行准确的评估，对订购方采购决策具有重要的指导意义。

目前，对装备维修性评估的研究取得了一定成果。在装备维修性评估指标体系构建方面，见文献［3-11］。目前的研究内容主要是通过装备维修性的定性要求来构建评估指标体系，对定量要求考虑较少，且评估对象多为导弹、船舶、航空产品、装甲车辆等，与雷达装备相关的研究较少。本文提出改进的IAHP-VIKOR 雷达装备维修性评估方法，构建了定性指标与定量指标相结合的雷达装备维修性评估指标体系，针对赋权过程，专家很难对指标给出精确数值的判断结果，采用基于区间数的赋权方法，使赋权过程更符合人的思维，提高了准确性；考虑到雷达装备维修性评估是复杂系统多属性评价问题，本文采用由Opricovic 首先提出的VIKOR 方法。通过对VIKOR 进行改进，以欧氏距离代替原有线性加权的方法计算群体效应值，更符合两点之间距离最短的公理；同时引入灰色关联系数，利用其处理“小样本”、“贫信息”、不确定问题上的优势，计算群体效应值和个体遗憾值，使得评估结果更为准确，兼顾了评价过程中的随机性、模糊性和灰色性，为鉴定定型阶段雷达装备维修性评估提供了一种有效方法。

1 雷达装备维修性评估指标体系构建

雷达装备维修性要求由管理要求、定量要求、定性要求与维修保障要求组成。按照指标体系建立的完备性、独立性、代表性、可比性、可操作性和简练性原则，构建由维修性综合参数、设计参数、时间参数和维修资源参数组成的雷达装备维修性评价指标体系，如图1 所示。

图1 雷达装备维修性评估指标体系

维修性综合参数由管理要求引出，主要有年维修器材费（万元）、站级故障修复比（%）等。

维修性设计参数由定性要求引出，如可达性、标准化与互换性、故障检测率（%）、模块化、识别标记、人素工程、维修安全性、防差错设施等。

维修时间参数由定量要求引出，主要有平均修复时间（min）、预防性维修时间（min）、重要部件更换时间（min）、首次翻修期（y）、冗余分系统切换时间（s）等。

维修资源参数由维修保障要求引出，主要有维修人员数质量、技术资料齐套率（%）、备件供应率（%）、维修设备与设施齐套率（%）等。

2 IAHP 确定指标权重

2.1 IAHP 法的求解步骤

IAHP 法确定指标权重的步骤如下：

Step 1 构建递进层次结构。对评估对象的影响因素进行分析，依据各因素之间的相互关系，构建不同的层级。下层因素影响上层因素，相同层的因素之间相互独立，互不影响。

2.2 引入三元联系数计算权重

由于区间层次分析法计算的权重为区间数，在评估计算时没有具体数值，不便对不同方案进行判断。因此，引入三元联系数，将权重区间转换为确定的数值。

3 改进VIKOR 法的雷达装备维修性评估模型

VIKOR 法是依据最大化“群体效用”和最小化“个体遗憾”，通过得到距离理想解最近的解来进行评价。具体而言，“群体效用”指评价对象的指标距离理想解的距离之和，距离越小越好；“个体遗憾”是各个指标距离理想解的最大距离，距离越小越好。因此，要求各方案提高正向指标的同时，兼顾短板，可简单理解为好的方面越来越好，差的方面也不能太差。

3.1 VIKOR 法的算法步骤

3.2 改进VIKOR 法

VIKOR 法通过计算距离理想点最近的妥协可行解，对方案进行排序的评价方法，计算简单，应用广泛。但其也存在不足之处，传统VIKOR 法以线性加权方法计算距离，该距离不是直线距离，不符合距离公理，导致计算结果偏大。同时，传统方法妥协方案集中的排序存在信息丢失的可能性。因此，针对上述存在的不足，本文在计算群体效用值时采用欧氏距离代替线性加权的方法，并引入灰色关联分析法，挖掘样本内在信息，将灰色关联度与群体效用、个别遗憾相结合，使得评价结果更加科学准确。

将式（12）改进为：

4 实例分析

以某型雷达装备在鉴定定型阶段a、b、c 3 种方案的维修性评估为例，采用本文提出的改进IAHPVIKOR 法，根据图1 构建的雷达装备维修性评估指标体系，对各设计方案的雷达装备维修性进行评估。通过对3 种方案的物理样机进行维修性试验，得到如表2 所示的各方案雷达装备维修性评估指标值。其中，指标C、C、C、C、C、C、C、C、C、C、C、C为定量指标，其指标值可以通过样机试验统计得出，指标C、C、C、C、C、C、C、C为定性指标，其指标值为专家打分的均值。专家打分时，“1”代表该指标得分极差，“2”代表该指标得分较差，“3”代表该指标得分中等，“4”代表该指标得分较好，“5”代表该指标得分极好。

表2 各方案雷达装备维修性评估指标值

4.1 IAHP 法确定评估指标权重

评估者根据表1 所示的比例标度，对图1 中的一级指标B、B、B、B，按顺序进行两两比较，得到判断矩阵A：

表1 比例标度的含义

同理，得出B所属的2 个二级指标的判断矩阵B，B所属的8 个二级指标的判断矩阵B，B所属的5 个二级指标的判断矩阵B和B所属的4 个二级指标的判断矩阵B：

根据式（2）～ 式（3）对判断矩阵进行一致性检验，得到各判断矩阵都具有一致性。

由式（4）计算区间判断矩阵权重，由式（5）～ 式（7）将区间权重转换为精确数值权重。表3～表7 为IAHP 权重、IAHP 转化精确数值权重以及传统AHP权重对比：

表3 IAHP 评估指标权重表I

表4 IAHP 评估指标权重表II

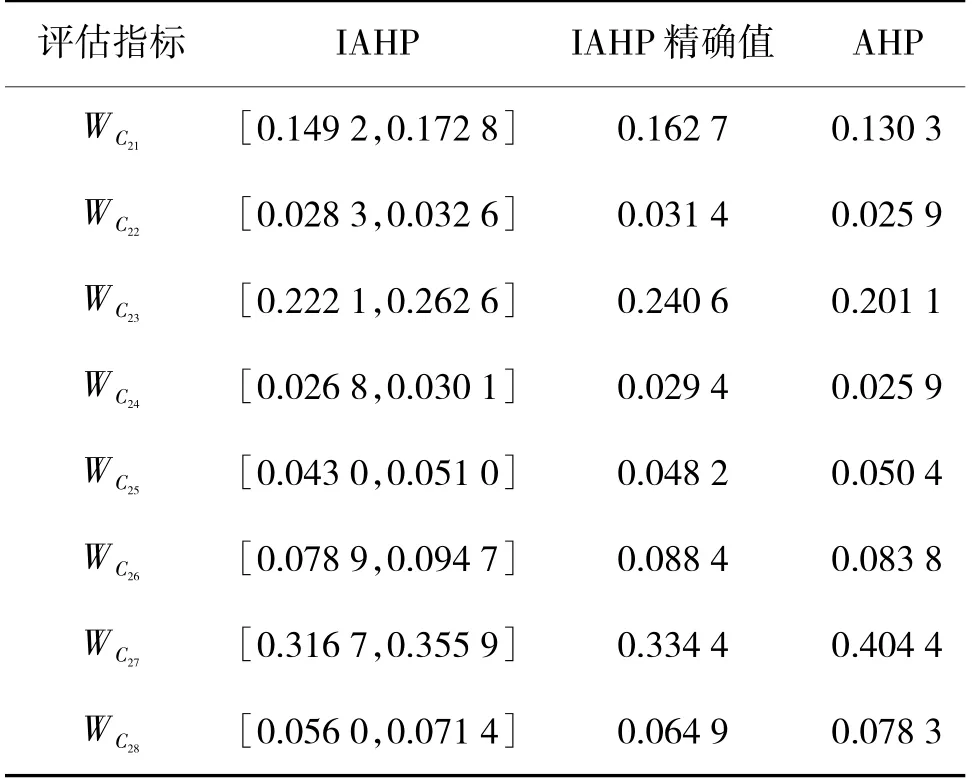
表5 IAHP 评估指标权重表III

表6 IAHP 评估指标权重表IV

表7 IAHP 评估指标权重表V

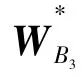
各底层指标相对于雷达装备维修性的综合权重W=（0.026 6，0.062 7，0.080 4，0.015 5，0.118 9，0.014 5，0.023 8，0.043 7，0.165 2，0.032 1，0.086 2，0.057 8，0.022 5，0.010 7，0.014 6，0.124 5，0.030 6，0.051 2，0.018 7）。

将传统AHP 所得权重与IAHP 精确值结果比较，如图2 所示。

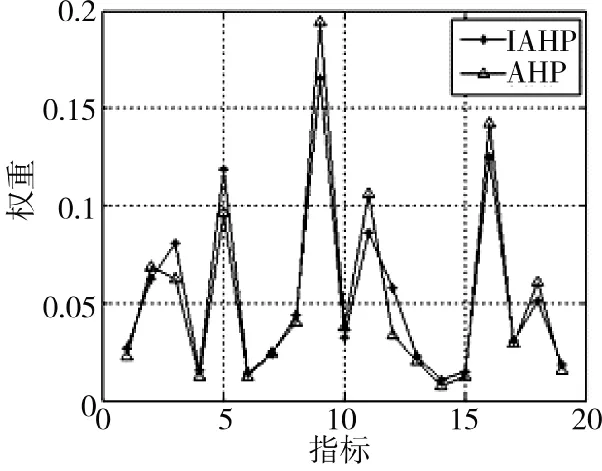
图2 AHP 与IAHP 精确值计算结果对比图

传统AHP 与IAHP 转化为精确数值的赋权结果趋势一致，但传统AHP 方法计算权重时存在个别指标被强化和模糊信息利用不充分的现象。而IAHP 方法计算的权重结果在保持结果稳定的基础上，充分挖掘了模糊信息，在对指标赋权的过程中，更符合人的思维方式。

4.2 改进VIKOR 法评估雷达装备维修性

在图1 所示的评估指标体系中，指标C、C、C、C、C、C、C、C、C、C、C、C、C为 效 益 型指标，指标C、C、C、C、C、C为成本型指标，根据式（9）～式（10）可得到正理想解Z和负理想解Z：

Z=（0.600 0，1，1，1，1，1，1，1，1，1，0.545 5，0.8，0.818 2，1，0.666 7，0.666 7，1，1，1）Z=（1，0.926 3，0.6，0.75，0.979 6，0.8，0.8，0.6，0.6，0.6，1，1，1，1，1，1，0.959 2，0.833 3，0.894 7）

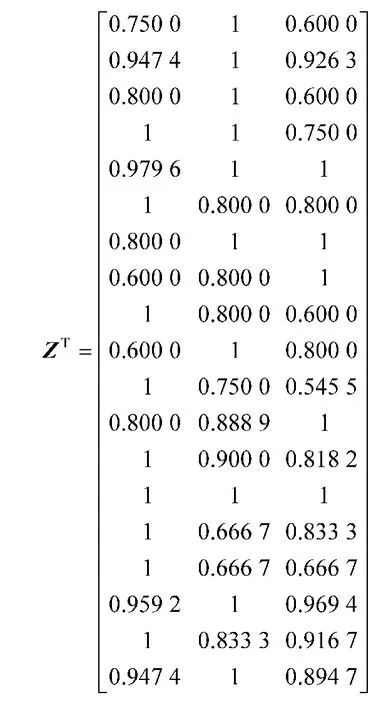
计算时，存在某方案项指标评价值一致的情况，如指标C，则令群体效应与个体遗憾值为0，即该指标与正负理想解距离均为0。根据式（12）、式（14）～ 式（22），取μ=0.5 以兼顾群体效值和个体遗憾值，计算改进VIKOR 方法后的群体效用值S、个别遗憾值R和评价结果值Q，结果如表8 所示。

表8 改进VIKOR 评估方法计算结果表

4.3 结果分析

通过调整传统与改进的VIKOR 方法中μ 的取值，观察不同取值对方案排序结果的影响，不同μ值下的评价结果与排序变化如表9、表10 所示。

表9 VIKOR 评估方法计算结果表

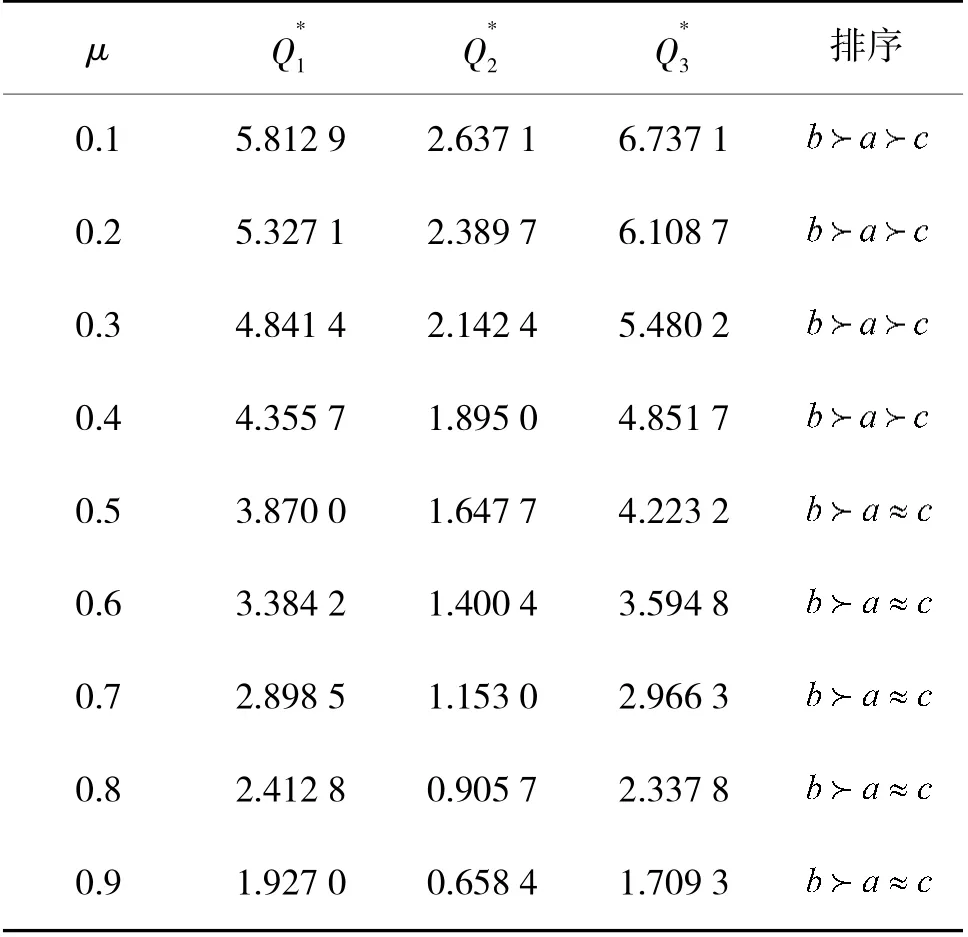
表10 改进VIKOR 评估方法计算结果表

分析可知，随着μ 值变化，改进的VIKOR 方法仍能筛选出方案b 是最优方案，证明了改进VIKOR方法评估结果的稳定性和有效性。

传统VIKOR 方法中，不同的μ 值计算出的Q、Q差值小于0.5，仅能根据Q确定方案b 为排序最优的解，方案a，c 为妥协解，并不能计算出3 种方案的全排序。

5 结论

本文构建了符合雷达装备维修性评估要求的指标体系；针对传统AHP 法处理模糊问题的不足，采用IAHP 的方法对指标体系进行赋权，引入三元联系数，将区间权重转化为精确权重值；提出了改进的VIKOR 方法，以欧式距离取代线性加权的方法计算群体效应值，克服了群体效用值结果偏大的缺点，同时引入灰色关联系数，充分挖掘数据信息，并根据决策者的个人偏好，得出方案的全排序，使得计算结果更加准确。实例验证该模型稳定有效，较传统方法更加灵活。为鉴定定型阶段雷达装备维修性评估问题提供一种方法。