园区互连型公路货运平台的大规模鲁棒运力资源分配问题研究

陈 玎 朱道立 杨 勇 赵 磊

(1.上海交通大学 中美物流研究院, 上海 200030; 2.上海交通大学 安泰经济与管理学院, 上海 200030;3.交通运输部科学研究院, 北京 100013; 4.上海交通大学 船舶海洋与建筑工程学院, 上海 200030)

0 引言

公路货运是我国最重要的货运方式之一,根据国家统计局资料显示,2018年公路货运量占我国货运总量的76.9%,超过了美国71%的占比。从公路货运总量角度看,2019年我国公路货运量有望突破400亿吨。但是,与庞大的货运市场不相匹配的是,我国货运行业始终面临着公路货运企业小、散、乱、差,行业集中度低的问题。以零担运输市场为例,我国公路零担货运行业集中度(concentration ratio top 10, CR10)仅有3%,而美国零担运输市场的行业集中度(CR10)高达75%,我国的整车运输的行业集中度甚至低于3%。这意味着我国公路货运市场的运力分散、运力资源浪费严重。“互联网+公路货运”模式是缓解这一局面,提高公路货运集中度,促进公路货运市场集约化发展的重要手段。随着“互联网+”的不断发展,我国出现了一批“互联网+”公路货运平台企业,他们借助互联网技术与平台经济思想整合物流资源,努力解决当前公路货运行业运力分散、运力资源浪费等行业痛点问题。

“互联网+” 公路货运平台的运营模式主要有交易撮合模式(轻资产化)和园区互连模式(重资产化)两种。交易撮合模式主要指货运平台公司通过商业推广将大量货主企业货运需求信息和运输企业信息汇集于平台。通过车货匹配方法,向货主企业推送满足需求的承运人,同时向承运人推送适合其承接的货运需求任务,达到交易撮合的目的。这一模式下平台公司主要通过车后市场进行盈利(例如:加油费、轮胎等耗材费、车辆保养费等)。我国交易撮合型公路货运平台的代表企业有:满帮、惠龙易通等。

另一种运营模式为园区互连模式。园区互连型平台公司与全国多个物流园区建立园区托管关系,将原本相互独立的园区日常运营标准化、规范化,并借此吸引各地依托物流园区的运输需求企业与平台签订运输合约,保证平台能向运输端用户提供充足稳定的运输需求。另一方面,平台通过发展自营运力和吸引承运商(包括小物流企业、大小车队甚至个体司机)加盟等方式,保证平台的运力端能够提供充足的运输资源。在公路货运市场供需两端资源充足的情况下,这种公路货运平台能发挥整合优势,科学决策合理调配运力资源,实现干线运输标准化、班列化运营,大力提高平台的服务质量,从而较大改进了平台双边用户的平台使用价值,提高了他们参与平台服务的积极性,从而促进了货运平台的良性发展。如图1所示。

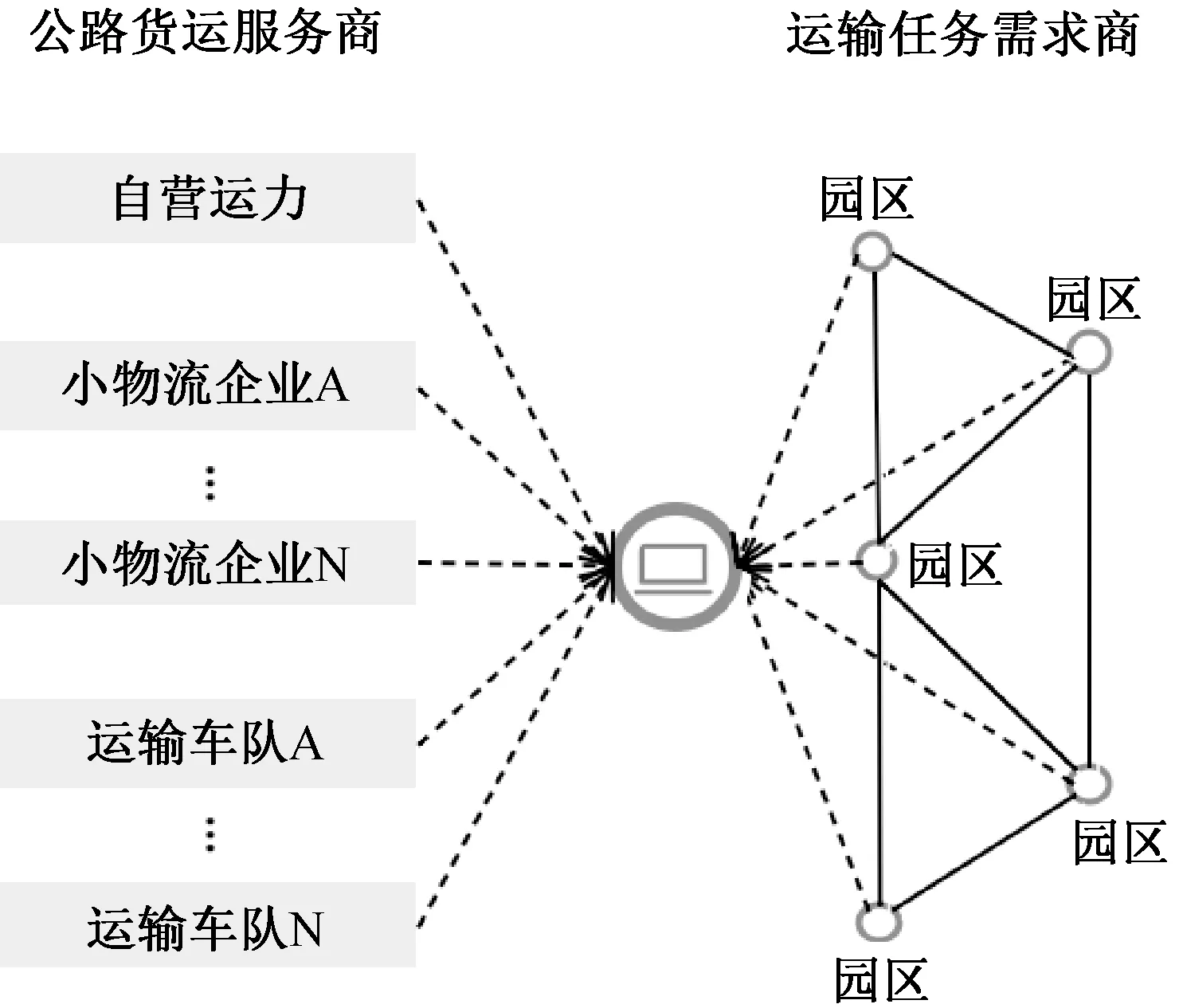
图1 园区互连模式Figure 1 Park interconnection mode

园区互连型公路货运平台运营管理系统主要由三部分组成:跨区域园区货运管理系统、运力管理系统和干线货运运营管理系统,如图2所示。其中,跨区域园区货运管理系统主要负责各物流园区货运运营管理、园区货运大数据分析、平台与园区合作模式设计等;运力管理系统主要负责运力状态跟踪维护、平台与运力资源合作设计等;干线货运运营管理系统则根据跨区域园区货运管理系统提供的运输需求信息和运力管理系统提供的可调配运力信息进行运力决策。通常,货运平台企业需要同时管理多个区域内物流园区及园区间干线运输,且不同区域的货运需求量和时效性要求不同。因此各区域的运输任务难以统一调配,需要各区域运营团队根据实时的运输需求,自行安排车辆发运与任务分配。但是货运平台在保证各区域货运任务的服务质量外,还需要考虑到各承运商利益平衡,各区域运力资源充足等因素。因此,目前园区互连型公路货运平台往往提前制定中长期货运决策(模板路径规划、运力资源分配),以中长期货运决策为指导与承运商签订相关合约,从而保证了承运商利益平衡和各区域运力资源充足。在中长期货运决策基础上,干线货运运营管理系统根据运营过程中的实时需求信息,制定科学的短期货运决策(日(周)路径计划、日(周)运输车辆排班),上述系统还能够利用运营过程中积累的数据进行大数据分析(决策效率/效益分析、运力资源评价、运价波动分析),并利用分析结果协助中长期运输决策方案的调整,从而形成了数据驱动的闭环干线货运决策系统,保证了平台决策的科学合理。在整个过程中,中长期货运决策的任务是以平台公司运营成本最低为目标,制定各路线运输需求对不同承运商的分配,而短期货运决策往往基于该“基础运力分配”进行“实时分配调整”,因此中长期货运决策的科学性极大的影响短期货运决策的质量,因此本文主要研究干线货运运营管理系统中运力资源分配这一中长期货运决策问题。

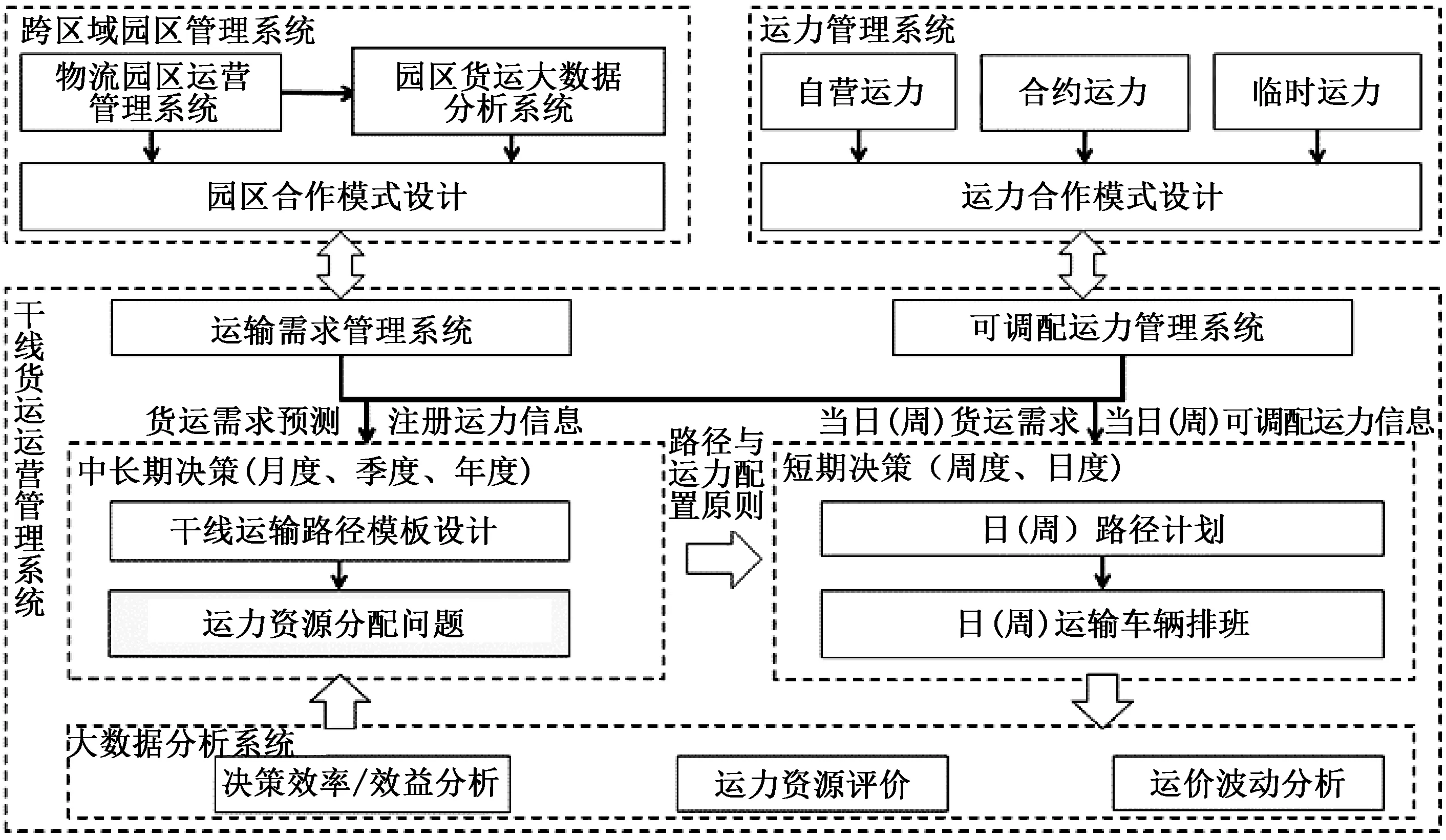
图2 园区互连模式运营管理系统Figure 2 Operation management system of park interconnection mode

货运平台企业主要利用双边平台的网络外部性,基于“互联网+”,大数据技术和平台经济管理思想,努力有效地为平台的运输需求方和运输服务方企业服务,从而提高平台双边用户的使用价值,吸引越来越多用户加入平台。如何科学运营平台,为巨大规模的平台双边用户提供高质量服务,是园区互联型公路货运平台管理者面临的巨大挑战。以我国某知名园区互连型公路货运平台为例,该平台预期在2020年覆盖千余条运输路线;与两万个以上的物流企业和三十余万个司机建立了加盟合作关系。根据国内公路货运市场规模估计:每年约有3000万货车司机,在万余条路线上承接共计343亿吨公路货运总量需求。巨大的市场规模意味着我国公路货运平台企业将面临庞大的双边用户规模,也意味着在公路货运平台企业运营中需要解决运力资源分配问题的规模庞大。此外,由于平台注册运力基数庞大、业务覆盖地理空间广阔,运输市场波动和运价波动是影响平台运力资源分配的关键因素。本文特研究具有规模巨大和运价信息不确定特征的运力资源分配问题。

本文的主要贡献如下:

(1)根据园区互连型公路货运平台的运力资源分配问题的特点,分别建立了大规模运力资源分配问题模型和考虑运价波动的鲁棒运力资源分配模型。

(2)针对考虑运价波动的鲁棒运力资源分配模型为复杂半无限规划的难点,给出了鲁棒运力资源分配模型的等价确定性鲁棒表达,将半无限规划问题转化为确定性非线性凸锥规划问题,并证明了二者的等价性;

(3)针对鲁棒运力资源分配模型的确定性鲁棒表达模型规模巨大,现有商业求解器难以求解的难点,本文提出了一种原始对偶并行算法对该模型进行求解。

(4)通过仿真实验,本文证明了鲁棒运力资源分配模型得到的分配方案具有更好的抗价格波动的能力,并能帮助平台科学设计保量合约策略;本文设计的算法能有效求解本文提出的鲁棒运力资源分配问题。

本文结构如下:文章第一节综述相关文献研究。在第二节,我们建立了运力资源分配模型,并在运力资源分配模型基础上建立了考虑运价波动的鲁棒运力资源分配模型,同时给出鲁棒运力资源分配模型的确定性鲁棒表达。在第三节,我们提出了一种适应求解大规模问题鲁棒运力资源分配模型的一阶原始对偶并行算法。在第四节,我们通过仿真实验,论证了本文提出算法的有效性,以及本文提出的鲁棒模型在科学决策的稳健性和实施合约签订策略方面的应用价值;最后,第五节总结全文。

1 相关文献综述

目前对于运力资源分配问题的研究主要集中在两个方向。第一个方向的研究主要是针对具体的货主信息,向其推荐合适的运力资源。Yuan研究了如何通过乘客的出行方式和出租车出的GPS轨迹,利用推荐系统向出租车司机推荐合适的出租车[1],这类方法也应用在了车货匹配问题中,Mallick使用强化学习的方法解决在线货运平台上,承运商如何作出运输订单决策的问题[2]。而贾艳丽等人通过设计考虑客户绿色偏好的车货匹配评价指标,并根据所建立的指标匹配体系以及所设权重建立多对多单边匹配模型,判断客户和司机的匹配程度,并进行推荐[3]。Gale提出了经典的双边匹配问题模型[4],朱江洪基于经典双边匹配问题的模型,提出了考虑不确定性语言评价表征属性信息的车货匹配方法[5],Gheraibia和Gouin-vallerand[6]设计了考虑二氧化碳排放,燃料消耗和运输拥堵程度等情况的货运推荐系统,为管理者提供能够满足客户需求的更有效的车货匹配方案。该类研究的成果也在满帮等企业得到了一定的应用[7],但该类研究只能向货主推荐运力资源信息,是否选择推荐的运力资源由货主决定而非平台。第二个研究方向主要研究对于货运车辆的指派问题,调度运输企业内部的各类车辆,从而完成规定的货运任务。Hoff在综述了当运输需求已知情况下,如何通过车辆路径问题(vehicle routing problem, VRP)以及其变种进行路径规划,并给出了相应的算法[8]。李冰对多车型动态车辆调配问题进行了研究,并提出了利用限行函数来近似目标函数中未来时段部分,从而得到合理的车辆调配方案[9]。Zeimpekis考虑了动态随机车队管理,在制订方案时考虑了当前的调度方案对未来各时段的影响,并综述了相应的模型和算法[10]。余以胜等人提出了改进Balance算法的车货匹配模型,引入了车货匹配平衡函数定义各车型的匹配情况,并根据车货之间的匹配关系对函数进行修正,使得决策结果相比贪婪算法在总收益上提高了18%[11],Powell研究了如何对于异质的大型卡车进行调度,并提出了相应的动态规划算法[12],常连玉等研究了对于无车承运人,如何对当前的运力资源进行指派,从而能够完成运输车辆的最优调度[13],Mu研究了如何对运力资源和运输要求相似的货源进行匹配[14]。该类指派调度问题虽然能够达到运力资源分配的目标,但其决策者往往是拥有运输车辆的运输企业,而非平台企业,并且其决策周期往往较短,数据规模也比较小。通过对运力资源分配问题的综述,我们发现目前的研究主要集中在运力资源的推荐与短期的运力资源的指派,缺乏对于园区互联型公路货运平台中长期运力资源分配问题的研究。

由于实际生活中很多问题都具有不确定性,自20世纪50年代左右出现了不确定优化的研究,例如机会约束规划[15],模糊规划规划[16],随机规划[17]等方式。模糊规划是通过不确定参数的模糊隶属函数来刻画不确定性,但由于模糊隶属度函数主要根据决策者的经验得出,因此该方法具有较高的主观性。随机规划是通过对数据进行分析,获得不确定参数的分布模型,之后通过期望、机会约束等方式,使得到的解在大概率情况下是最优的,该类方法在车队的指派问题中也有着应用[10]。鲁棒优化则由Soyster于20世纪70年代提出[18],并由Ben-tal,Nemirovski等人发展成鲁棒优化理论[19-21]。相比于模糊规划,鲁棒优化利用集合的方式对不确定变量进行描述,因此不需要不确定参数的模糊隶属度函数和分布模型,同时,鲁棒优化的解考虑了不确定集合内最坏的情况,因此其结果较为稳健,最优决策方案对不确定因素波动的敏感性较低。近年来,鲁棒优化已被广泛应用于供应链管理、项目管理等管理领域[22-24]。

2 园区互连型公路货运平台运力资源分配模型与考虑运价波动的鲁棒运力资源分配模型

2.1 运力资源分配模型

货主(运输需求方)通过与平台签订运输合约,确保平台能为其提供充分的运力资源,并保证运输质量。而平台的承运商(包括自营运力和加盟企业/司机)加盟平台的目的是希望得到充足稳定的运输任务与合理运输价格。在中长期决策之初,园区互连型公路货运平台通常根据货主提出的运输任务需求、货运需求量预测以及平台注册运力对平台运力资源进行分配。平台在运力资源分配时,需要考虑平台双方用户的价值需求,签订的运输合约以及平台自身发展需要,将货主的不同区域的干线运输任务,合理的分配给大量具有不同运输范围、运价特征、供给能力的运输承运商,从而使得在中长期情况下,各类干线运输任务能够得到尽可能地满足,同时最大程度的降低运输成本。本节介绍运力分配问题的数学模型,首先给出如下定义:

(1)集合

Γ(j)={i:(i,j)∈}:可分配给干线的承运商j∈集合;

Γ(i)={j:(i,j)∈}:表示在承运商运输范围内需求干线i∈的集合。

(2)参数

cj:货运干线j∈上的平均单位运输收入;

dj:货运干线j∈上的运输需求总量;

c′ij:承运商i∈在承接货运干线j∈时的单位运输成本;

Pj(yj):凸的光滑单调递增函数,描述需求损失量与损失惩罚的关系,其中j∈;

si:承运商i∈能够提供的运力资源上限;

hi:平台在合约中向承运商i∈承诺提供的最低运输需求;

ωi:平台在合约中向承运商i∈承诺提供的最低运输需求占承运商能提供运力资源上限的比例,即

(3)决策变量

大规模运力资源分配模型主要考虑如何在决策周期内对大量不同的承运商提供的运力资源进行分配,从而使其能够满足货运干线运输需求,因此设每个承运商在各干线上分配的干线运输任务的比例为决策变量。即:

xij:向承运商i∈分配在货运干线j∈的运输任务的比例;

yj:当运输需求无法被满足时,货运干线j∈的需求损失量;

由此,大规模运力资源分配问题可表示为如下的优化模型:

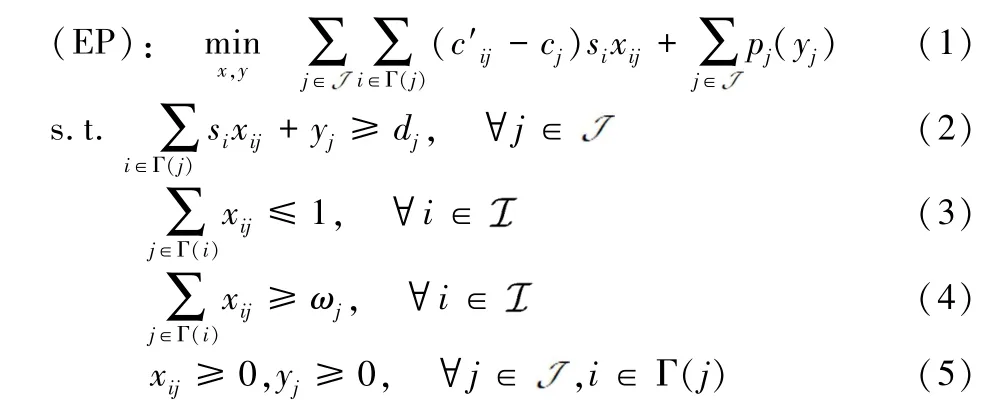
其中,(1)为目标函数,由两项组成,第一项表示了平台的总的净运输成本,该成本由需要平台支付给承运商的成本扣除运输收入组成。第二项表示当无法满足运输任务时,需要承担的惩罚成本为约束条件,约束(2)为需求满足约束,即对于每条货运干线,分配的运力资源的数量必须满足干线的需求,yj则表示无法满足货运干线j上运输需求的数量,该类约束共有m条。约束(3)为运力资源限制约束,即分配的运力资源的总量不能超过物流企业能够承接的总量,该类约束共有n条。约束(4)为运力资源合约约束,即平台通过与承运商签订合约的方式,保证承运商i至少能够分配到一定量的运力资源,该类约束共有n条。约束(5)为非负性约束,一共有m×(n+1)条。

一般来说,当需求无法预期完成时,平台需要按照与货主之间的合约,向货主进行赔偿。由于不同运输干线的货物价值与服务水平不同,签署的合约也有所不同,因此惩罚成本P(y)也会随之不同,常见的惩罚函数可用一个单调函数来表示,例如eayi-1(a＞0)。运输服务高的干线对应的惩罚函数的递增率会更大。不失一般性,我们在这里用非线性光滑凸函数Pj(yj)(j∈)来刻画不同合约情况下的需求损失的惩罚。

为方便鲁棒模型的构建与推导,我们将问题(EP)等价地表达为矩阵向量形式问题(EP′)。令承运商集合为={1,…,n},平台承接的货运干线集合为={1,…,m},令运力资源分配问题需要决策的变量数为t=mn,1m表示m维1列向量,0m表示m维0列向量。则(EP′)需要引入如下向量参数:

lij:判断承运商类别i∈是否为承运商业务范围内的可运输干线j∈,如果可以运输则lij=1,否则lij=0。

l∈ℝt:承运商的运营范围判断向量,l=(l11,…,l1m,

x∈ℝt:决策变量xij(i∈,j∈)向量,x=(x11,…,

y∈ℝm:决策变量yj(j∈)向量

c∈ℝt:承运商的单位净运输成本,j∈),其中

d∈ℝm:货运干线j∈上的需求向量,d=(d1,…,

ω∈ℝn:平台提供给承运商i∈最低运力需求占承运商运力上限比例向量

s∈ℝt:承运商能够提供的运力资源参数si(i∈)向量,

同时,我们还引入如下参数矩阵:

这样,运力资源分配问题(EP)可以表示为如下矩阵向量的等价形式。

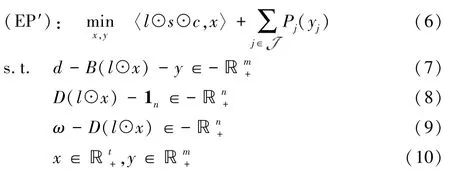
其中⊙为矩阵的哈达玛积运算。

2.2 考虑运价波动的鲁棒运力资源分配问题模型

在中长期决策过程中,往往需要参考一些基于历史数据分析的辅助决策系统给出的信息(如图2所示)。在实际情况下,随着运输市场的不断变化,运输价格往往会产生波动,因此,在进行长期决策时,通过参考不同承运商的运价波动情况,会获得更优的资源分配决策。如平台企业在不考虑运输价格波动的情况,就可能会青睐运价较低的运输企业,在决策时向这些企业分配较多的运输任务。但实际情况下,由于承运商与平台签订的合约中明确规定,加盟商能够按照市场情况对运价进行调整。因此若该类承运商在承接大量运输任务后,在决策周期内上浮运价,则会造成平台企业的运输成本的大幅上升,严重甚至会导致资金链断裂等风险,因此本文通过考虑分析不同承运商的历史运价数据,从而制定出能够一定程度上抵御价格波动特性的运力资源分配计划,进而帮助平台减少上述损失风险。

鲁棒优化作为一种不确定性最优化方法,能够基于历史运价数据,通过构建不确定集合的方式描述参数的不确定性,管理者是基于该不确定集合进行科学决策。如考虑了不确定集合中最坏的情况,就能得到具有稳健性的决策。由此,本节提出了基于价格波动的鲁棒运力资源分配模型。在决策时通过参考所有承运商的运价的历史信息,进而构造运价的不确定集合,由此帮助平台制定更符合平台服务环境和平台风险承担能力的运力资源分配计划。

令运输价格c的不确定集合为表示为U={c∈ℝt,其中为期望运输价格向量,即通过历史数据获得的不同加盟承运公司在不同干线上的成本的期望,A∈ℝt×t为通过历史数据获得的不同加盟承运公司之间运价的协方差矩阵,ρ≥0为决策稳健程度的系数。令为波动因素,取模。 这种对价格的刻画方式,将运价的波动纳入了对运输价格的表达,使得模型能比期望运价模型更综合的考虑运价均值和运价波动情况,更合理的选择对应的承运商,从而增强了模型的抗运输价格波动能力。考虑运输价格波动的鲁棒运力分配问题(RP)具体如下。

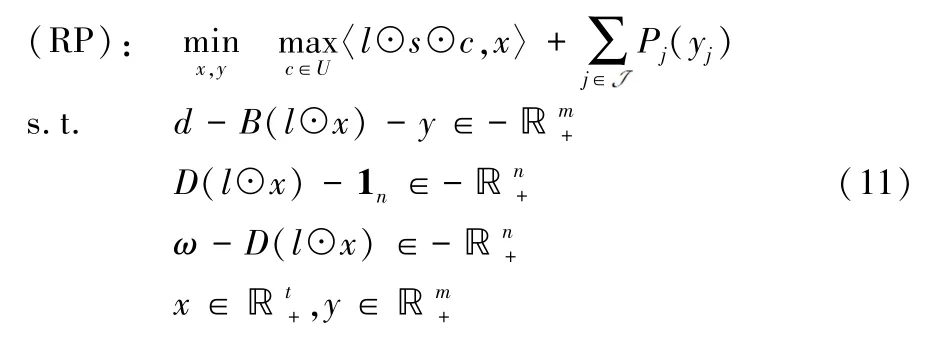
由于(RP)问题是一个复杂的半无限规划,它包含无限个约束条件,直接求解十分困难,因此本文根据Ben-Tal提出的鲁棒对等转换理论(robust counterpart)[20],将其转化为确定性鲁棒表达。

命题1假设不确定集合‖ζ‖∞≤ρ},其中,A∈ℝt×t,ζ∈ℝt,则有

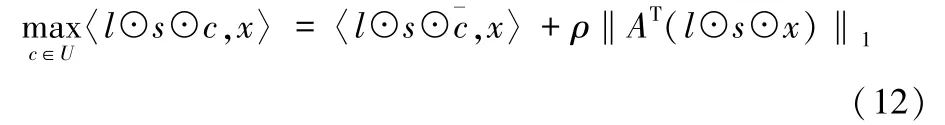
根据命题1,可以得到鲁棒运力资源分配问题模型的确定性鲁棒表达如下:

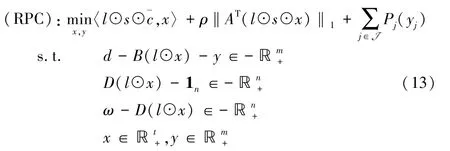
根据一阶锥的定义,可以将(RPC)转为非线性凸锥约束问题 :

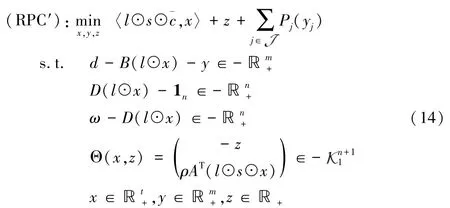
3 求解鲁棒运力资源分配模型的一阶原始对偶并行算法

对于问题(EP′)与(RPC′),其变量数随着承运商和货运干线数量增加直线上升,同时,由于决策周期较长,园区互连型公路货运平台需要进行决策的承运商规模和货运干线的数量都非常之大,这就导致了该类运输资源分配问题的规模十分大。例如,按照国内目前某企业给出的规模数据,该企业每月需要制定近两万承运商在千余条路线上的运力资源分配计划。则问题(EP′)与(RPC′)将会有千万级别的决策变量与约束条件。更进一步,随着平台经济的不断发展,如果公路货运平台企业能够承接全国1%的公路运输需求,则代表着平台企业每月需要制定面向几十万承运商的几千条路线上运输的资源分配计划,此时问题(EP′)与(RPC′)的决策变量更是趋近十数亿。对于这类复杂的大规模问题,常见的算法由于数据量过大,计算资源要求高的限制,很难甚至无法进行求解;同时,由于模型中会有锥约束,目标函数中Pj(yj)是非线性凸函数,导致CPLEX等常见的商业求解器也无法进行求解。因此,本文基于Zhao和Zhu[25]提出的一般非线性凸锥约束规划的VAPP算法,提出一种求解大规模资源分配问题的一阶原始对偶算法对本文提出的大规模鲁棒资源分配问题进行求解。该方法通过将问题分解为多个能够并行求解的子问题,分别求解后,通过对偶进行协调,进而迭代得到最终的计算结果(如图3(a)所示)。该方法不同于顺序迭代求解的串行算法(如图3(b)所示)需要在每个子问题上都要使用全部的数据带来的对高性能计算资源要求。VAPP算法的每个子问题相互独立,因此只需要通过增加求解子问题计算资源的数量,便可提高运算的效率,因此具有更好的横向延展性,更适合于大规模优化问题的求解。

图3 VAPP算法和串行算法迭代流程Figure 3 VAPP algorithm and serial algorithm iterative process

下面,我们将根据Zhao和Zhu[25]提出的有效求解非线性锥规划的VAPP方法,给出求解(RPC′)的一阶原始对偶算法。为了简化表达,我们可以将模型(RPC′)写成如下形式:

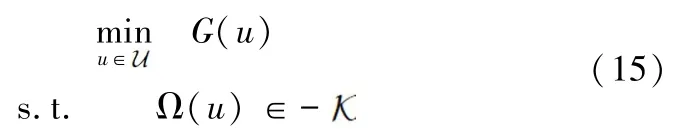
根据增广Lagrangian的对偶理论,模型(15)的增广Lagrangian函数可表示为:

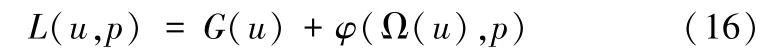
其中,Lagrangian乘子p∈ℝm+3n+1,φ(Ω(u),p)=为在的共轭锥*上的投影。本文涉及的一阶锥的共轭锥为,而

{ℝm+}和{ℝn+}共轭锥为其本身,其投影为投影对象的本身。Zhao和Zhu在[25]中提出求解问题(14)的原始对偶迭代方法:

在上一次迭代获得的uk和pk基础上求解原始子问题,得到uk+1:

在原始子问题解uk+1和上一次迭代获得的乘子pk基础上求解对偶子问题,通过投影得到pk+1:

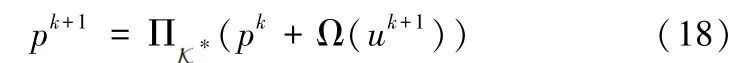
该方法在原始方向上采用了线性化和规则化处理,因而原始优化子问题(17)可分解为各变量的独立优化问题。对偶问题(18)是投影计算。

具体算法流程如下:

算法1=0m,λ02=λ03=0n,λ04=0n+1 :设置参数:α为一个足够小的参数,最大迭代次数K for k=1,…,K计算原始方向子问题: xk+1=arg min初始化:x0=0t,y0=0m,z=0,λ0〈¯c,l⊙s⊙x〉+〈qk1,B(l⊙x)〉+〈qk2,D(l⊙x)〉-〈qk3,D(l⊙x)〉+〈¯qk4,A⊥(l⊙s⊙x)〉+1 2α‖x-xk‖2(19) yk+1=arg min x∈ℝt+y∈ℝm+〈▽P(yk)-qk1,y〉+1 2α‖y-yk‖2 (20) zk+1=arg min z≥0(1-^qk4)z+1 2α‖z-zk‖2 (21)计算对偶方向子问题: λk+1 1+(d-B(l⊙xk+1)-yk+1)) (22) λk+12=Πℝn+(λk 1=Πℝm+(λk 2+(D(l⊙xk+1)-1n)) (23) λk+1 3+(D(l⊙xk+1)+ω)) (24)3=Πℝn+(λk 4+Θ(xk+1,zk+1)) (25)End for输出:xK,yK λk+1 4=Πimages/BZ_178_460_2667_484_2698.pngn+1(λk∞

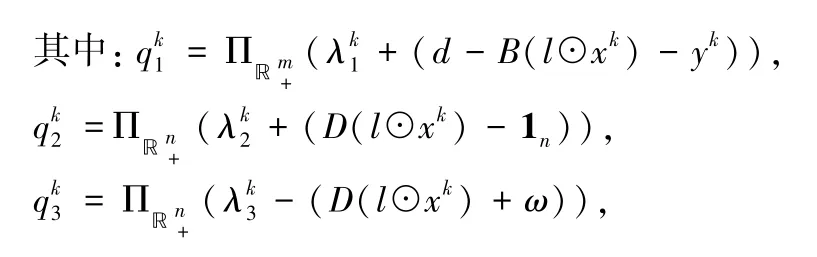
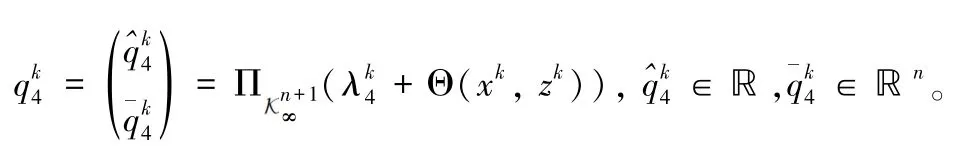
特别需要指出的是:通过对原始方向优化问题(23～25)的分析,各个子问题均存在如下闭合表达式:

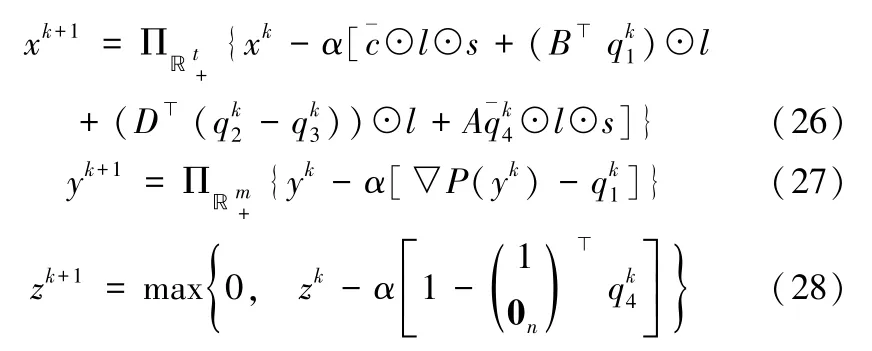
可以看到,VAPP算法在原始问题上的x,y,z的求解是相互独立的,即可以分别利用计算资源,通过闭合表达式(19～21)在原始方向上对x,y,z的进行并行迭代求解。同时,对于向量x,y,z的求解,由于向量的每个元素的更新均相互独立,因此对于x,y,z的每个元素也能够进行并行求解。通过这种并行求解的方式,将计算任务分摊到多个计算资源上,解决了大规模资源分配问题中,计算资源无法存储和计算大规模变量的问题。

此外,通过分析我们不难得到问题(RPC′)为非线性凸锥规划问题,根据凸分析理论,凸问题(RPC′)的KKT点即为问题的最优解。算法迭代点wk=(xk,yk,zk,λk1,λk2,λk3,λk4)给出KKT映射如下:

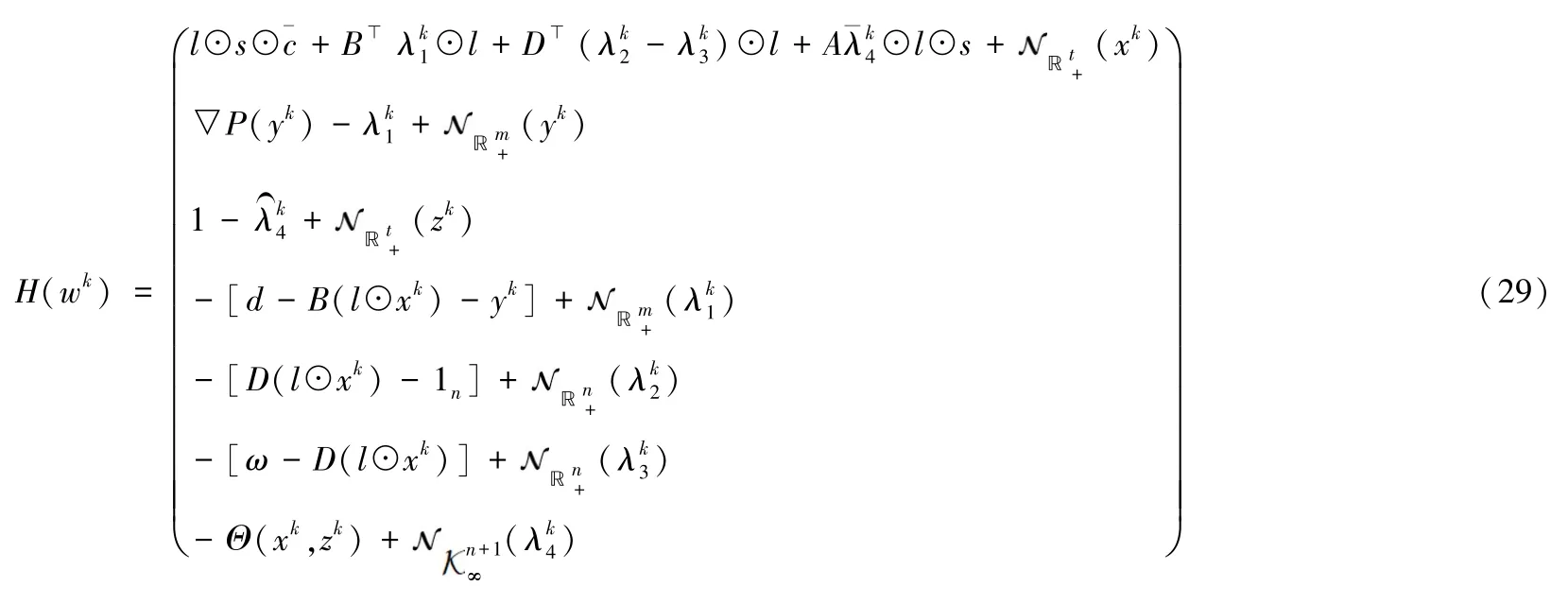
定义1(问题(RPC′)的ε-近似解)如果点满足如下不等式

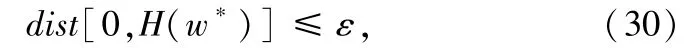
我们称w*为凸问题(RPC′)的ε-近似解。如果ε=0,w*则为问题(RPC′)的最优解。

命题2假设序列{wk}由算法1生成,则有存在δ＞0,使得如下不等式成立

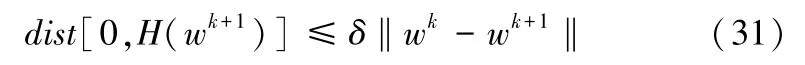
RCP′满足Zhao和Zhu给出的定理1中[25]给出的所有条件,因此算法产生序列{wk}有界,并收敛到问题的KKT点,即‖wk-wk+1‖→0。根据命题2,‖wk-wk+1‖≤ε′可作为算法的终止条件,其中ε′=ε/δ,δ为一个不随算法迭代变化的正数。如果‖wk-wk+1‖≤ε′,算法的迭代点wk+1可看作问题(RPC′)的ε-解。

4 仿真实验

4.1 仿真环境设置

由于计算资源的限制,本文仿真实验中设置运输路线为10条,承运商为100家,则具有一千多个决策变量和两千多条约束。对线路和承运商的仿真数据设置如下:

由图1可知,平台会将承运商根据其企业规模、风险等级及签约要求等信息进行分类并签订不同类型的合约。因此,本实验将承运商分为4类:临时承运商、短期合约承运商、中期合约承运商以及长期合约承运商,每类承运商25家,每类承运商能够提供的运力为1.357万吨,所有承运商能够提供的运力为5.428万吨。总的运输需求为3.6187吨。每家承运商的运输能力以及营运范围由仿真系统随机生成。

一般来说,平台与临时承运商不签订保量合约。因此临时承运商价格受市场影响较大,运输市场的淡旺季等因素会对临时承运商的价格造成很大的影响。临时承运商虽然运价均值较低,但运价的波动性较大,平台将与其他三类承运商签订不同期限的运力合约。合约时间越长,平台向承运商提供的运力报价也会相应提高,同时承运商的运价波动也会相应减小。仿真系统按照上述原则生成了100家承运商20天内的运输价格数据集。其中承运商运价均值越高,对应的方差越高,代表运价的波动性越大。将100家承运商20天内的运输价格数据集按照承运商类型进行汇总,得到表1的运价均值数据。根据表1得到的运价数据,结合设定的平台利润率情况,仿真系统生成每条路线上对货主方面的运输价格cj。

表1 运输路线上各类承运商及平台对货主的运价均值(单位:元/吨)Table 1 The mean freight rate of various kinds of carriers and platform income on the transport route (in yuan/ton)

4.2 算法有效性分析

4.2.1 实验目标

算法有效性分析实验通过对算法迭代的相对误差进行分析,证明算法的有效性。

4.2.2 实验方案

定义相对误差ek=‖wk-wk+1‖,由于问题(RPC′)满足Zhao和Zhu给出的定理1中[25]给出的所有条件,因此算法产生序列{wk}有界,并收敛到问题的KKT点。则根据命题2,ek可以作为算法有效性的表征。

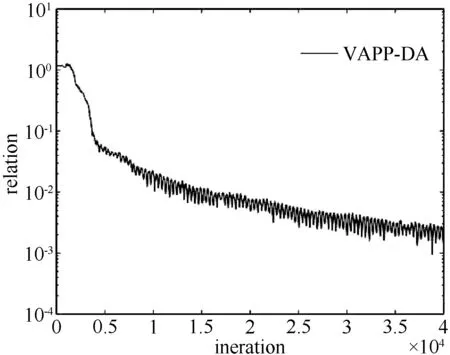
图4 算法有效性分析Figure 4 Effectiveness analysis of the algorithm

4.2.3 实验结论

由图4可以看到,随着算法的逐渐迭代,相对误差ek逐渐减小并趋近于0,说明算法正逐渐收敛到问题的KKT点。由此,图4证明了本文提出的算法能够有效的求解 (RPC′)鲁棒资源分配问题。

4.3 鲁棒模型决策有效性分析

4.3.1 实验目标:

鲁棒模型决策有效性分析实验主要通过对运力资源分配模型(EP′)和鲁棒运力资源分配模型(RPC′)计算结果进行比较,证明鲁棒运力资源分配模型(RPC′)对于抵抗运价波动上的有效性。

4.3.2 实验参数设计:令表示为干线i上无法满足的货运量的单位惩罚成本,令惩罚项为仿真所需的运力数据来源于4.1中的仿真环境。其中运力资源分配模型(EP′)运输价格为仿真环境中每家承运商的运价均值,鲁棒运力资源分配模型(RPC′)的运价信息与运价波动信息来源于仿真环境4.1中的承运商运价数据集。根据仿真数据的特点,取三种不确定集合:ρ=0.001,ρ=0.0005,ρ=0.0001,产生三种鲁棒模型:(RPC′-1),(RPC′-2),(RPC′-3)。

4.3.3 实验方案:

按照仿真环境中得到的运价均值数据以及运力数据,得到问题(RPC′-1),(RPC′-2),(RPC′-3),(EP)的运力资源分配计划。而后按照仿真环境中给出的不同承运商的运价均值和方差,生成实时运价,进而能够得到不同运力资源分配计划的运输成本。将上述过程重复100次,则可以得到长期运行情况下,问题(RPC′-1),(RPC′-2),(RPC′-3),(EP)的运力资源分配方案成本的均值和方差情况,实验结果如表2。

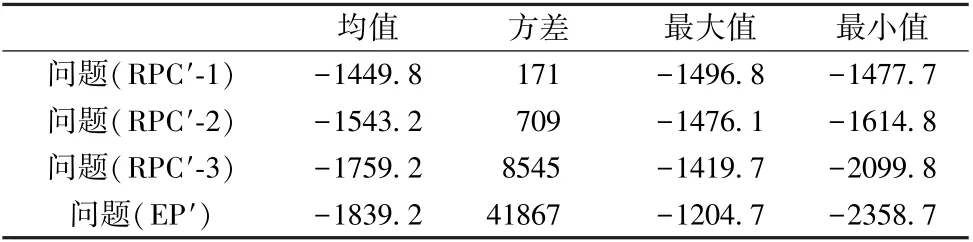
表2 鲁棒有效性分析中不同决策模型多次仿真实验系统成本结果(单位:万)Table 2 System cost of simulation experiments with different decision-making model in robust effectiveness analysis (in ten thousand)

4.3.4 实验结论

根据实验计算和分析,我们能够得到如下结论:

(1)鲁棒运力资源分配模型具有更好的抗价格波动能力,而运力资源分配问题(EP′)受价格波动的影响较大。在100次的随机价格波动中,问题(RPC′-1)和(RPC′-2)的方差,最大值以及最小值均没有发生太大的变化;问题(RPC′-3)的方差相比前两者较大,并且最小值发生了比较明显的变化;问题(EP′)的方差最大,并且其最大值和最小值的差异也比较明显,说明其会根据价格的波动产生比较明显的变化。

(2)鲁棒运力资源分配模型得到的运输成本的均值高于运力资源分配问题(EP′)。相比于问题(EP′),鲁棒运力资源分配模型的运输成本较高。随着决策稳健性的提升,其运输的成本也会相应增加。

4.3.5 管理建议

由鲁棒模型决策有效性分析实验我们发现,更强的抗价格波动能力往往会导致运输成本的提升。因此企业需要根据其发展阶段与自身的发展策略,对决策策略进行调整,制定出符合企业发展阶段的运力资源分配计划,使得企业能够有效应对运输市场的价格波动,保证企业的健康发展。

本文提出鲁棒运力资源分配模型,不仅能够在运营层面上帮助企业制定长期运力资源分配策略,同时能够通过对ρ的调整实现对决策稳健性进行调整,进而帮助企业理解不同决策策略下的抗价格波动能力与运输成本之间的关系,从而能够在战略层面上指导企业制定出更符合企业发展阶段的长期运力资源分配决策。

4.4 保量合约设计分析

4.4.1 实验目标:

揭示平台合约策略对运力资源分配的作用,为平台管理者提供设计保量合约策略的科学思路。

4.4.2 实验参数设计:

本次实验设计了四类合约策略,不同的合约策略表示平台对不同类型运力的偏好程度。其中,合约策略1表示平台对四类运力均不签署运力合约;合约策略2表示与短期合约承运商签订较大的保量合约,而对长期合约承运商签订较小的保量合约;合约策略3表示与三类合约运力签订同样大小的保量合约;合约策略4则表示对长期合约承运商签订比较大的保量合约,而对短期合约承运商签订比较小的保量合约。具体的保量合约签订情况如表3所示。

表3 保量合约设计分析中不同合约策略下每类运力的保量合约签订情况Table 3 The signing status of the volume contract of each type of capacity under different contract strategies in the analysis of the volume contract design

4.4.3 实验方案:

按照仿真环境中得到的运价均值数据以及运力数据,分别得到四种合约策略下的运力资源分配计划。而后按照仿真环境中给出的不同承运商的运价均值和方差,生成实时运价,进而计算能够得到不同合约策略下的运输成本。将上述过程重复100次,则可以得到长期运行情况下,四种合约策略下的运力资源分配方案成本的均值和方差情况,实验结果如表4所示。

表4 保量合约设计分析中不同合约策略多次仿真实验系统成本结果(单位 万)Table 4 System cost of simulation experiments with different contract design strategies (in ten thousand)

将不同合约策略下,各类承运商在分配结果中的运力资源占比情况进行统计,得到表5所示结果。

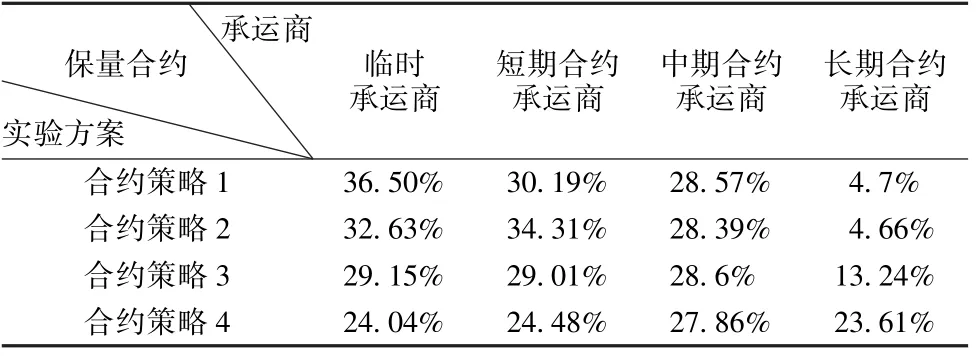
表5 保量合约设计分析中不同合约策略下运力资源占比情况(单位:万)Table 5 The proportion of capacity resources under different contract strategies in contract designing analysis (in ten thousand)

4.4.4 实验结论

根据上述实验,我们能够得到如下结论:

(1)合约签订策略会对运力分配抗价格波动能力产生影响。由表4我们可以看到,平台与中长期运力类型承运商签约较高运输合约比例,会提升系统的抗价格波动能力,但同时也会增加系统运输成本。

(2)合约签订策略也会对不同类型承运商的运力分配结果产生明显影响。由表5能够看到,当平台与短期合约承运商签订较高的保量合约(合约策略2),将导致短期合约承运商运力占比明显上升;而随着向中长期合约承运商签订保量合约比例的上升(合约策略3,4),中长期合约承运商在整个运力资源分布中的占比明显上升。

4.4.5 管理建议

合约的签订策略会导致运力分配决策结果抗运价波动能力的变化。平台需要根据其发展阶段,合理的选择合约策略,才能够保证其健康长效的发展。例如,在平台发展初期,可能需要与短期合约承运商签订较大比例的合约,进而保证平台能够吸引到足够的运力资源。而在平台发展的稳定阶段,为保证平台有更好的抗价格波动的能力,平台需要适量降低对短期合约承运商的保量合约签订比例,提高对中长期合约承运商的保量合约签订比例。

本文提出的鲁棒运力资源分配模型,能根据企业不同的合约策略,得出对应的运输资源分配方案。因为企业能够对不同合约策略的反应结果有直观和科学的认识,从而能够在战略层面上,指导企业制定出符合自身发展的合约签订策略。

5 总结

本文研究了“互联网+”模式下,园区互连型公路货运平台对运输资源有效组织分配问题,针对平台企业用户规模大,价格波动敏感的特点,本文提出了考虑价格波动的鲁棒运力资源分配模型,由于这一模型为复杂半无限规划问题,因此本文利用对偶范数和一阶锥的定义,给出了这一问题的可计算确定性鲁棒表达,并应用Zhao和Zhu提出的VAPP算法框架,设计了能够并行运算的且在多项式时间内收敛的求解算法。

最后,本文通过仿真实验证明了本文算法的有效性。同时,实验证明了本文提出的算法在战略层面和运营管理层面均有很好的适用性。在战略决策层面,本文提出的鲁棒运力资源分配模型能够对结合运力分配稳健性策略和合约签订策略仿真,可帮助企业制定出符合自身发展期望的运输分配方案,促进企业实现企业战略决策智能化。在运营管理层面,本文提出的鲁棒运力资源分配模型能够结合企业实际的运营情况,制定出满足双边用户需求的最优运力分配方案,提高企业的运营效率和质量。