基于细节层次模型的公共自行车调度方法*

胡正华 周继彪 周涵林 张敏捷

（1.宁波工程学院建筑与交通工程学院 浙江 宁波 315211；2.浙江大学信息与电子工程学院 杭州 310063；3.同济大学交通运输工程学院 上海 201804）

0 引言

随着城市化进程的不断加快，汽车保有量日益增长，道路交通的拥堵问题变得越来越严峻，致使许多城市的主干路高峰时段的车速不足20 km/h。持续性的道路交通拥堵及其带来的诸如尾气排放和能源浪费等一系列社会问题严重阻碍了城市经济的健康发展[1-2]；而另一方面，面对不断加剧的城市交通问题和日益恶化的生态环境，“绿色出行”的理念也越来越受到各国政府的关注，大力发展城市公共交通已经成为社会各界的共识。作为“低碳”和“绿色”的出行方式，城市公共自行车的出现受到了许多城市的热捧。它不仅能够缓解城市道路的交通压力，还也可以解决公共交通“最后一公里”的难题。继北京、上海、广州之后，许多中小城市也相继推出了城市公共自行车的租赁服务。然而，随着2015年以来移动互联网快速发展普及，共享单车入驻各大城市，凭借无桩化设计、移动支付定位、智能解锁等创新型技术，共享单车和电动车在一、二线城市中迅速崛起，城市公共自行车系统受到了不同程度的冲击[3]。一些城市甚至暂停了对公共自行车系统的运营。公共自行车系统未来要如何发展成为1个难题。

然而，共享单车在给出行带来便利的同时，也引发了诸如“车辆乱停乱放”“调度不及时”“废弃后无人回收”等一系列问题[4]。特别是在一些大城市里，共享单车的过量投放，使得单车的车辆堆满了人行通道，这就给行人的出行带了极大的不方便，严重影响了行人的道路安全；不仅如此，在许多住宅小区的门口和公交站台附近经常堆满了各种各样的单车或者电动自行车，严重影响了市容市貌和交通秩序。尤其是电动自行车普遍存在“车辆运行安全风险高”“电池污染严重”“火灾隐患突出”等问题[5]。基于此，交通运输部发布了《关于鼓励和规范互联网租赁自行车发展的指导意见》，明确提出“不鼓励发展互联网租赁电动自行车，建议各地审慎对待，从严掌握”。许多城市的政府部门相继出台了相应的政策方针，开始限制甚至取缔了共享单车和共享电动车的使用；有些城市则是保留了部分共享单车的投放使用，但为了有效的控制乱停乱放的现象，设定了指定的停车点；还有一些城市则是设定了共享单车的可使用区域，超出区域之外则无法为用户提供服务。在这样的背景下，城市的公共自行车系统的发展又一次迎来了春天。

然而，城市的公共自行车系统依旧存在其发展的瓶颈。首先，对于公共自行车而言，其自行车和站点的数量与共享单车相差很大。从分布密度上看，共享单车的投放密度已经比公共自行车高出十余倍。其次，政府对公共自行车系统维护的投入力度不够。尤其是对于自行车车辆的调度，许多站点在早晚高峰时段仍然出现“无车可借”或“无位可还”的现象，导致许多市民放弃使用公共自行车出行，这就大大降低了公共自行车的使用率，严重制约了公共自行车系统的发展[6-7]。如何高效的将自行车在各个租赁点之间进行调度，进而使租赁点上的自行车数量与用户需求相匹配依然是研究学者关注的话

题[8-9]。

Haider等[10]通过使用定价的方案来激励用户从相邻的站点借还自行车，结合单级重构的双层优化模型，从战略上最大限度地减少不平衡自行车站点的数量。实验结果表明该方法能够有效降低了公共自行车系统的运营成本。但由于该方法假设时间价值对所有的用户都是相同的，不仅如此，用户对于价格的变化具有不同程度的敏感性，自行车使用者的异构概率有待进一步研究。Kadri等[11]将自行车车辆的再平衡问题简单的建模成1个带有附加约束条件的旅行商问题，以最小化车辆再平衡时间作为模型的目标函数，通过大量的实验验证了方法的有效性。Pal等[12]结合1种混合整数线性规划方法，进一步提出了1种混合嵌套邻域搜索算法，该方法在解决大型公共自行车系统的静态调度问题时既有效又高效。通过验证实验表明，所提出的算法优于禁忌搜索算法而具有很强的竞争力。Cruz等[13]讨论了当只有1辆调度车可供车辆的调度时，如何在满足所有自行车站点的需求，且不违反调度车辆负载限制的基础上找到1条调度成本最低的路线，提出了1种基于迭代局部搜索的启发式方法，获得了较好的效果。但是在验证解决方案是否可行时，需要耗费大量的时间，使得算法的效率得不到应有的保障。Ren等[14]旨在最小化包括自行车车辆库存和调度成本在内的运营成本，提出了2种混合整数规划方程，以找到调度车辆最优的调度线路以及需要调度的自行车数量。通过实验验证了所提出的方法比现有解决方案拥有更低的运营成本。但由于每个自行车站的库存水平没有与仓库的库存一起考虑，该方法仍然存在一定的局限性。Chiariotti等[15]采用“出生-死亡”的过程来对自行车站点的占用率进行建模，并确定重新分配自行车的时机，他们采用图论来选择车辆调度的路径和所涉及的自行车站点。模拟实验表明该方法是1种能够适应波动性质的动态调度策略，因而优于传统的静态调度方案。但为了使建立的模型在数学上可处理，对其做了相应的简化，在应用到现实的公共自行车系统之前，还需要进一步的完善。Hu等[16]使用历史数据和预测数据来评估车辆的调度需求，以便在调度范围内避免站点的2次服务，并提出了1种基于时间窗的满意度模型来评估用户对公共自行车系统的满意度。使用真实数据进行的实验表明，所提出的算法优于常规算法。但是模型中并没有考虑运输车的数量对调度成本的影响，自行车库存变动率系数也是需要在进一步的研究中考虑的重要因素。

综上所述，现有的公共自行车调度方案大多基于静态的调度模型，不能针对公共自行车系统的动态性做出实时的调整，而且建立的模型所考虑的影响因素过于简单，在应用到现实的公共自行车系统之前，还需要进一步的优化。而一些基于动态调度模型的算法又过于复杂，很难针对每个城市公共自行车系统的发展现状得到有效的应用。本文在已有调度算法的基础上，结合目前城市公共自行车系统的发展瓶颈，提出了1种基于细节层次模型的公共自行车调度方法。该方法结合人类认知和思维的过程，以1种准动态且相对简单、灵活的方式对城市公共自行车系统的调度方案进了优化，从而有效地改善了城市公共自行车的运营效率。

1 问题的描述与建模

公共自行车调度问题解决的是由于公共自行车借/还需求在时间和空间分布的不均衡而引发的“借车难”“还车难”问题，即在调度车数量一定的情况下，确定各个租赁点需要调入或调出的自行车数量以及调度车辆最优的调度路径，使各个自行车租赁点的车辆数能够在时空范围内达到相对的平衡，从而在最大程度上满足市民的出行需求。

为了简化模型求解，本文假设公共自行车系统中自行车租赁点和公共自行车的总数是有限的。一方面，对于每辆自行车而言，只有被锁在某个租赁点或者正在被用户使用2个状态。另一方面，假设在城区范围内设有一定数量的自行车调度中心用于负责其周边的自行车站点的车辆调度，每个调度中心配有摆渡车对自行车进行调度，其运载能力保持一定。利用公共自行车站点的历史借还车数据结合深度学习模型来预测未来一定时间段内各个站点上的借还车需求。当站点桩位的锁车比低于或者超过一定的范围后，调度系统将会自动预警，进而生成相应的时间窗，并提醒管理中心的工作人员对相关站点进行车辆的调配。

对于用户而言，如果1个自行车站点上无可用自行车或者站点无空闲桩位可以归还自行车，则该站点无法对用户提供服务，用户只能放弃使用公共自行车出行，这样就降低了公共自行车站点的服务能力。因此，在调度车辆在尽可能少的返回调度中心的前提下，如何根据各个租赁站点的需求量，设计合理高效的调度方案，使得调度车辆从调度中心出发有序通过各个有调度需求的租赁站点后又回到调度中心。最大可能的满足居民的出行需求，提高自行车站点的服务质量。同时，还要兼顾到公共自行车系统车辆调度的成本，使调度车辆的行驶的路程最短或者调度时间最短。因此，本文设计的公共自行车车辆的调度方案将调度车辆的运输成本和用户满意度2个方面作为优化自行车调度方案的目标函数。

1）运输成本。要使得调度车辆的运输成本最低，只要确保车辆的行驶路程最短即可。车辆1次调度的运输距离见式（1）。

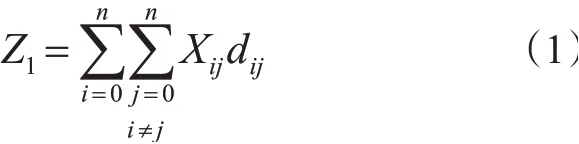
式中：Xij为决策变量，Xij=1代表在某1趟调度中，运输车辆从站点i行驶到站点j，Xij=0代表运输车辆没有从站点i行驶到站点j；dij为站点i至站点j的距离，m；n为在某一趟调度过程中需要进行调度的站点总数。

2）用户满意度。用户满意度可以转化为不满足时间窗的罚时成本。具体而言，为了保证用户能够在站点得到所需的服务，调度车辆应尽可能在用户期望的时间内完成对站点的调度。利用软时间窗来对调度车辆的到达时间进行约束，到达时间距离期望时间点越远，惩罚成本越高。公共自行车调度模型的时间窗罚时成本见式（2）。

式中：Wi为决策变量，表示站点i是否需要被调度；ti为调度车辆到达站点i的时间；[ ]Li，Ui为站点i的时间窗，Li表示站点i期望的最早被调度时间，Ui表示站点i期望的最晚被调度时间；epu为不满足时间窗时的早到罚时成本，lpu为晚到罚时成本。如果调度车辆在Li之前到达站点i，产生过早调度损失成本epu×(Li-ti)；如果调度车辆在Ui之后到达站点i，产生延误调度成本lpu×(ti-Ui)，否则，不产生时间窗惩罚成本。

综上，公共自行车调度模型的目标函数见式（3）。

式中：α，β为运输成本与时间窗罚时成本所占的权重；Z1为运输成本；Z2为时间窗罚时成本。

2 模型求解

2.1 站点的相似度

传统的聚类算法都是基于站点的空间位置关系，即利用站点之间的欧式距离来衡量不同对象的相似程度而进行的[17]。而在对城市公共自行车站点进行自行车车辆的调度时，还应该考虑到自行车站点之间的借/还车情况，将它作为评价站点相似度的指标之一[18]。将公共自行车站点之间的欧氏距离以及站点之间的借/还车情况来进行聚类的。这样会使得聚类结果中的自行车站点更具有同质性，而不同簇之间的自行车站点更加异质性。即采用这样的方法得到同1个簇中的自行车站点不仅在空间位置上比较靠近；同时，这些站点之间的借/还车情况也比较相似。这也为后续的公共自行车调度提供了更好的数据基础。因此，本文借鉴了文献[18]的设计思路，以站点之间的空间距离作为衡量站点间相似度的主体，同时将借/还车情况作为权重，与空间距离一起作为衡量2个站点之间相似度的依据。

2.2 遗传算法

遗传算法是以决策变量的编码作为运算对象，以目标函数值作为搜索信息，通过模拟生物的基因、染色体和遗传进化的方式来寻找最优个体的过程，并使用适应度函数值来评价个体的优劣程度。遗传算法基于概率规则，参数对其搜索效果的影响也比较小，而且可以避免传统的搜索方法在对多峰分布的搜索空间进行搜索时容易陷入局部极值点的缺陷，因此具有较好的全局搜索性。同时遗传算法具有可扩展性，易于与细节层次模型混合使用。

2.3 长短期记忆网络

长短期记忆网络（long short-term memory，LSTM）是循环神经网络的1种，也是1种时间循环神经网络，具有长时记忆功能。它可以很好地刻画具有时空关联的序列数据，可以计算出不稳定时间序列中各个观测值之间的依赖性，也解决了长序列训练过程中存在的梯度消失和梯度爆炸的问题。因此，LSTM通常用于时间序列数据预测的目的。本文基于LSTM网络模型，并结合公共自行车的借/还车序列来预测未来的借/还车需求。

2.4 基于细节层次模型的公共自行车调度算法

1976年，Clark提出了细节层次模型的概念[19]。它是指在不影响画面视觉效果的条件下，根据物体模型的节点在显示环境中所处的位置和重要度，决定物体渲染的资源分配，降低非重要物体的面数和细节度，从而获得高效率的渲染运算，完成对复杂场景进行快速绘制。目前，细节层次模型在多个领域都得到了应用。

基于划分的层次聚类方法是以所有对象在同1个簇中作为聚类的起点，然后按照一定的规则逐个地将每个集群划分为更小的集群的过程[20-21]。从整体上看，基于划分的层次聚类方法也是1种按照某种规则自顶向下分裂1个簇的过程，直到簇中只有1个对象或者满足预设的终止条件为止。在众多的基于划分的层次聚类方法中，结合谱聚类方法的层次聚类算法是使用较为广泛的算法之一。谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看作空间中的点，这些点之间用边连接起来。距离较远的2个点之间的边权重值较低，而距离较近的2个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，进而达到聚类划分的目的。

基于谱聚类的层次聚类算法，设计了与之相对应的城市公共自行车调度策略。由前文的分析可知，基于谱聚类的层次聚类算法其实是1种粒度由粗到细的划分过程，而基于细节层次模型的公共自行车调度算法的本质则是1种调度粒度由大到小，不断细化的过程。

在得到了相应的站点划分区域以后，首先利用划分粒度最大的区域作为顶层的调度单元，其次利用每个簇中站点的自行车借/还需求来制定相应的调度方案，并将其作为最高层级的自行车调度策略。对于每个调度单元，依次获取下一层级的公共自行车站点的聚类划分方案，同样作为相应的自行车调度单元，形成第二层级的调度策略。按照这样的规则遍历由基于谱聚类的层次聚类算法得到的不同层级上的站点簇，同时根据同一层级内不同簇之间自行车的借/还总需求来制定相应的调度方案。这样把每一层的调度策略整合到一起，最终形成1个类似树结构的调度方案，也就是本文提出的基于细节层次模型的城市公共自行车调度算法，其完整的流程见图1。

图1 基于细节层次模型的公共自行车调度算法流程图Fig.1 The flow chart of the rebalancing algorithm based on the hierarchical scheme for bike-sharing system

综上所述，基于细节层次模型的公共自行车调度算法实质上是1个由粗到细统筹、规划的过程。这也充分体现了人类从宏观到微观的认知过程。当决策者在实施车辆的调度时，总是先从宏观上来统筹和规划车辆的调配，然后再逐步细化到1个更小的区域来调配车辆，而不会一开始就着眼于某个自行车站点的调度需求。因此，本文提出的公共自行车调度算法也符合人类认知和思维的过程。

3 案例分析

本文的实验采用Python语言开发，其测试与运行环境均在Windows 10操作系统下进行。实验首先基于公共自行车站点的相似度矩阵，利用谱聚类算法对所有站点所在的区域进行划分。接着对每个划分得到的区域递归地执行谱聚类，形成空间范围由大到小的站点簇，作为不同层级上自行车的调度单元。然后从顶层的调度单元开始，利用站点的历史借/还车数据和LSTM网络模型预测在未来时段内各个调度单元之间的借/还车总需求；同时，结合遗传算法对每一层级上的各个调度单元进行调度；最后将不同层级上的调度方案叠加在一起，形成1种调度粒度由粗到细的调度策略。通过与传统的调度方案对比证明本文提出的公共自行车调度算法具有明显的优越性。

3.1 公共自行车站点区域的层级划分

宁波市公共自行车系统经过多年的发展，已经基本覆盖到每个县市区。到目前为止，该系统已经取得了可观的实施效果。宁波市市民可以根据市民卡或者公交卡在公共自行车站点刷卡借/还公共自行车，并且每个站点上都详细记录了用户的借/还车刷卡记录。以主城区为例，该区域内共有公共自行车站点169个，锁车桩5 428个。

选取宁波市主城区的公共自行车站点作为实验对象，对其进行了细节层次的聚类划分，见图2。其中的圆点代表区域中的每个公共自行车租赁点。首先，将主城区范围内的所有公共自行车站点的集合视为1个簇，作为层次划分方案的起点。然后，调用谱聚类方法对该节点所包含的自行车站点进行聚类划分，形成在空间范围内较原始的站点簇更小的子簇，作为第1层级的划分方案，见图2（a）中的区域1，2，3。从图2中可以清楚的发现，通过1次聚类划分，整个公共自行车站点所在的区域被划分成了3个子区域；这些站点簇从空间范围上来看，占据的空间还比较大，包含的站点数量也相对较多，站点的分布密度较小，排列比较稀疏。最后，对一次划分得到的每个簇，再次构建相似度矩阵并结合谱聚类算法进行进一步的划分，得到第2层级的划分方案，见图2（b）。按照这样的划分过程不断地继续下去，直到每个簇中站点之间的平均距离小于1 km（根据实施过程中的外部条件，如负责调度的车辆数、站点之间的平均距离等因素来综合考虑），则整个划分的流程结束，见图2（c）。随着不断的划分，得到子簇的空间范围会越来越小，每个子簇中的自行车站点的数量也越来越少，站点的分布密度越来越高。将多个不同空间范围大小的簇叠加在一起，就形成了1个划分粒度由大到小，类似树状结构的自行车站点区域的层级划分方案。

图2 宁波市公共自行车站点的层级划分示意图Fig.2 Sketch map of the hierarchical division of the stations from bike-sharing system in Ningbo

从宏观上看，基于谱聚类的层次聚类方法就是将公共自行车站点所在的主城区范围按照不同的划分粒度进行由粗到细的划分，形成分布区域由大到小的空间区域。这也为本文将要提出的基于细节层次模型的公共自行车调度算法提供了数据准备。

3.2 基于细节层次模型的公共自行车调度实例与分析

为了减少计算量，实验将层级划分方案中最后1层上的自行车站点形成的簇作为最底层的调度单元，即不再对该单元中的站点进行划分。将当前层级中每个簇所在的自行车站点区域作为每个层级的车辆调度单元，结合各个单元内自行车借/还需求的总和，对自行车进行调度。然后把每个层级上的车辆调度方案叠加在一起，形成1个调度粒度由粗到细的公共自行车调度方案。

实验利用历史借/还车数据（2017年1月1日—6月29日）并结合长短期记忆网络LSTM对2017年6月30日早高峰（07：30—08：30）时刻城区各自行车站点的借/还车需求进行了预测。同时，本文设置公共自行车站点的报警阈值为0.4和0.6，即当站点的车辆饱和度超出阈值区间[0.4，0.6]时，站点发出预警信号，然后生成以超过阈值的报警时间为中心，每个层级上固定长度的时间窗，最后统计各个调度区域内总的借/还自行车需求量，见表1。

表1 早高峰时各调度单元的自行车需求与相应的时间窗Tab.1 Demand and the corresponding time window of each rebalancing unit during morning peak

利用遗传算法求解调度车在当前层级上不同小区域之间最佳的调度方案，尽可能减少调度车辆返回调度中心进行车辆装配的次数，从而减少车辆的调度成本。其中，遗传算法所涉及的核心参数包括种群规模100，迭代次数为1 000，变异率为0.10，车辆行驶速度为14.4 km/h，装卸1辆自行车的时间为50 s，调度车辆的最大运载量为300，初始装载量为150。最终求解出各个层级上站点的调度方案，见表2，调度方案的示意图见图3。

图3 调度方案的示意图Fig.3 Sketch map of the rebalancing scheme

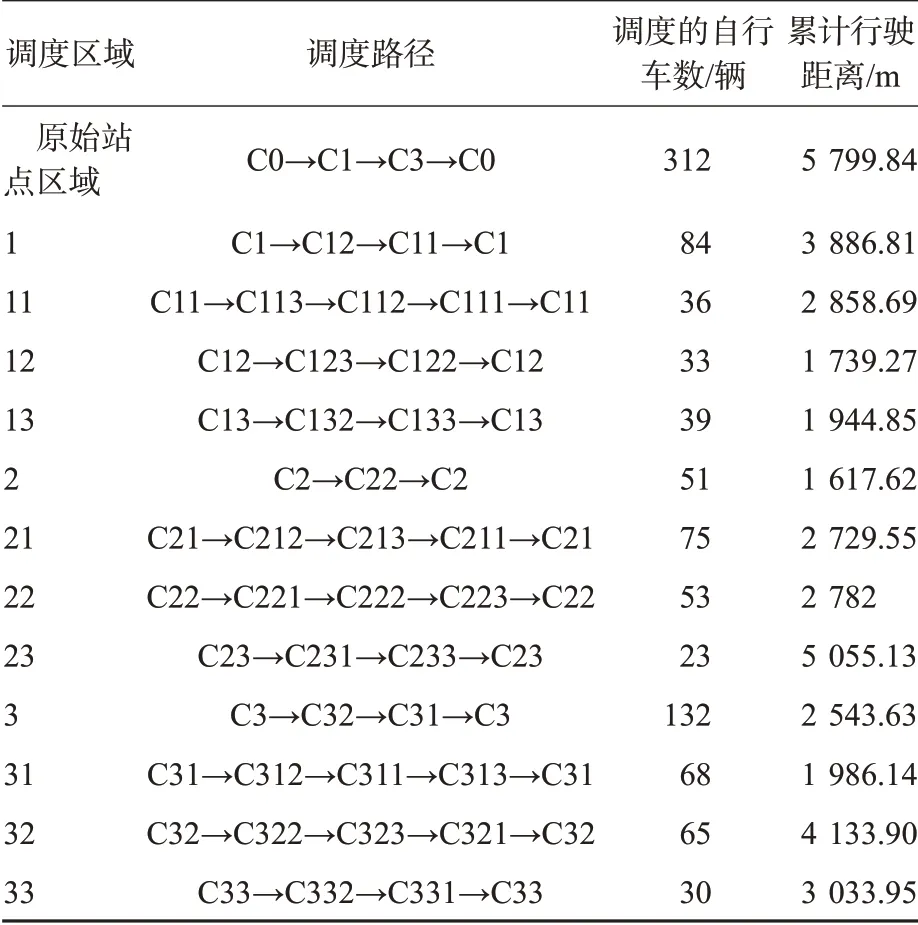
表2 不同层级上各调度单元之间的调度方案Tab.2 Rebalancing scheme between each unit on different levels

调度车辆首先从第1层级上的调度中心出发，先后经过该层级上需要进行调度的站点簇，最后返回调度中心，完成第1层级的调度任务（例如C0→C1→C3→C0，在该算例中区域2处于自平衡状态，因此无需进行调度）。然后在当前层级的各个调度单元内，继续统计每个簇中下1个层级上各个子簇之间的自行车使用需求，再次调用遗传算法计算最优的调度路线，使调度车辆从当前调度区域内的某个调度单元出发，先后经过本区域内每个需要进行调度的站点子簇，最后返回到出发的调度单元，完成第2层级的调度任务（例如C1→C12→C11→C1）。这个过程一直执行下去，每辆调度车都依据上1个层级的调度结果，结合本层级上各个站点簇之间的自行车使用需求，并结合遗传算法计算最优的调度路线对车辆实施调度，直到完成所有站点的调度任务为止。

3.3 对比实验与分析

本文将提出的基于细节层次模型的公共自行车调度算法与传统的调度算法（不分层调度）进行了比较试验，为了使结果更加的清晰，在本次实验中，我们只安排1辆调度车进行调度，同样利用遗传算法对每趟调度路径进行求解（参数同前）。实验结果见图4。

图4 传统调度方案与本文调度方案对比图Fig.4 Comparison of the traditional rebalancing scheme and the one proposed in the article

如果使用传统的调度方法，则调度车辆将从调度中心出发直接对所有站点进行调度，通过遗传算法计算出针对每个站点的调度方案，见表3，调度车在整个过程中的行驶总长度为700 005.58 m，有效调度时间为291.70 min。而基于本文提出的调度方案，首先将实验区域进行层次聚类划分，并在此基础上进行细节层次的车辆调度。各子区域中每条调度路径的总长度见表4。通过对不同层级上统计数据的累加，计算出使用本文提出的调度方法，调度车的行驶总长度为40 111.38 m，有效调度时间为167.13 min，与传统的调度方法相比，大约提升了42.7%的调度效率。

表3 传统调度方法的调度路径长度与调度时间Tab.3 The length of the path and the rebalancing time of the traditional method

表4 基于层次调度方法的路径长度与调度时间Tab.4 The length of the path and the rebalancing time of the hierarchical method

可见，本文提出的调度方法在没有增加人力成本和实施难度的前提下，就可以有效缩短总的调度距离和调度时间。这样可以尽可能满足用户对自行车的使用需求，提高城市公共自行车系统的整体服务能力。因此，这是1种经济、实用的公共自行车调度方案。在具体的实施过程中，当调度车到达当前调度区域的中心点后，先对下层的子区域内实施调度（有点类似于对树的深度优先遍历方法），然后在下层的子区域内完成调度后回到当前层后对下1个调度单元进行调度。当调度车辆比较充裕的情况下，可以在当前层级安排调度车辆来实现集群之间的调度，并在下1个层级的每个子区域分配其他调度车辆执行调度。

城市公共自行车车辆的调度算法是解决公共自行车车辆借/还需求时空分布不均衡问题的关键。实验证明本文提出的公共自行车调度方法可以较好的提升城市公共自行车系统的调度响应速度和服务质量，降低系统的维护成本。如果将本文的方法应用于各大城市的公共自行车系统的运营管理，不仅有助于提升公共自行车的服务水平，提高市民对公共自行车系统的满意度，更能有效地引导人们使用公共自行车代替小汽车出行，从而改善城市道路交通拥堵的现状。

4 结束语

本文以满足借/还车需求最大化和调度成本最小化为优化目标，结合基于谱聚类的层次聚类算法，研究了1种基于细节层次模型的公共自行车调度方案。算法首先将所有自行车站点的集合看成1个簇，采用谱聚类算法对其进行聚类划分，然后将得到的子簇再利用谱聚类算法进行聚类，形成在空间范围上更小的簇。按照这样的规则不断执行下去，形成对公共自行车站点区域不同粒度的划分。在每个层级结构中，将每个子簇所在的空间范围看成1个调度单元，统计各个单元内自行车的借/还需求总量，并使用遗传算法求解每个层级上最佳的调度方案。最后，将每个层级上的调度方案叠加在一起，形成1种调度粒度由粗到细的调度方案。

并以宁波市主城区的公共自行车系统为例，详细验证了该算法的可行性和实用性。对比实验证明，该调度方案能够有效的减少“借车难”“还车难”的情况，最大程度的满足借还车需求，提升自行车站点的服务能力，提高用户使用公共自行车的满意度水平。因此，本文的研究可以为城市公共自行车车辆的调度提供有效的理论依据，也可以对相关部门进行公共自行车调度提供重要的指导意义。

本文仍存在一些不足。例如，在构建模型时，时间窗的长度设置成了固定值。文中并没有讨论这个值的设置对算法结果的影响。在后续的研究中，还将针对站点借/还车需求的分布特征，分析设置不同时间窗长度对算法的影响，从而确定时间窗的最优值。最后希望本研究的贡献能给从事该领域的研究人员带来一些启发或指导，我们将进一步研究城市公共自行车系统的智能调度策略。