基于MPCA建模的间歇过程故障分析

张静静 方 彬 秦 兰 刘佳微 张博健

(河北建筑工程学院，河北 张家口 075000)

0 前 言

随着现代工业产品的高质量精度，高质量和多功能品种市场需求，工业化生产更多地需要依赖于一种间歇生产过程.间歇控制过程这种控制系统一般通常是非线性的，时变，滞后的，模型一般是不完全确定的，因此对关于间歇控制过程这种系统控制技术问题的理论研究，具有一定的科学理论和技术实践上的应用价值.

故障检测方法有很多，对此类方法的研究也越来越多，其中聚类分析的研究在不同系统的数据处理中也显而易见的凸显了优势.但是传统聚类分析方法采用欧氏距离进行计算，它将不同属性的变量等同对待，这一点有时并不能满足实际的要求.而采用马氏距离可以排除变量之间相关性的干扰，克服指标变量不同量纲不同权重所造成的误判.

本课题研究改进了目前传统的欧氏距离聚类方法，采用普拉马克欧氏时间距离聚类分析方法进行聚类分析.在诸如Matlab等编程语言环境中，实现基于马氏距离的时段间歇划分过程并将时段划分算法用于程序库的设计[1-2].并使用pensim青霉素发酵模拟软件进行间歇时序的青霉素发酵过程数据测试.

1 基于MPCA的故障检测原理

1.1 以批次开展为基础的MPCA方法原则

多向主元分析方法需要每个子数学模型都具备独立的子数据空间[3]，这一系列的子数据空间组成了MPCA模型[4].原理是将三维间歇过程的矩阵操作数据进行二维展开，然后对其进行标准化处理，最后得到的数据是通过PCA建模的.其建模实质是把一个庞大的数据空间，沿一个轨迹分割成一系列子数据空间，并分别构成多个子数据模型，并由多个子数据构成非线性多元统计数学模型[5].

1.2 主元分析方法原理

给定在正常测量情况下可以工作的一个测量数据集，有m个过程变量，n个观测值，将该数据集写为矩阵(X∈Rn×m)的形式，其中每一列代表一个测量变量，每一行代表一个样本.矩阵X如式1所示[6].

(1)

利用PCA对样本数据进行建模.定义标准化的样本x协方差矩阵为：

(2)

对其特征值进行分解，并按特征值的大小降序排列.PCA模型对X进行以下分解：

(3)

T=XP

(4)

其中P∈Rm×A为负载矩阵，由S的前A个特征向量构成.T∈Rn×4为得分矩阵，T的各列被称为主元变量，A表示主元的个数，也是得分矩阵的列数.

基于PCA方法进行过程监控，通过对两个多元的统计数据进行监视，T2和SPE实现了间歇生产过程的正常运作和实时监测.其中，T2统计量的控制限可采用F分布来计算，公式如下[5]

(5)

其中，A为主元个数，I为建模批次数，α为显著性水平.

SPE统计量，是指预测误差平方和指标(Squared prediction error,SPE)，表示模型偏离主元件与模型预测距离的统计测量误差值.可以用符合下式的计算方法式来计算出SPE统计量的控制限[4]：

(6)

(7)

(8)

其中，mk为建模数据集中所有批次测量数据在第k个时刻SPE统计量的均值，vk为其对应的方差.

完成模型后，根据标准轨道分段的情况，对在线数据进行了阶段分类，得各点T2和SPE值[6].

(9)

tk,i=Xk,iPk

(10)

Sk=diag{λk,1,λk,2,…,λk,R}

(11)

(12)

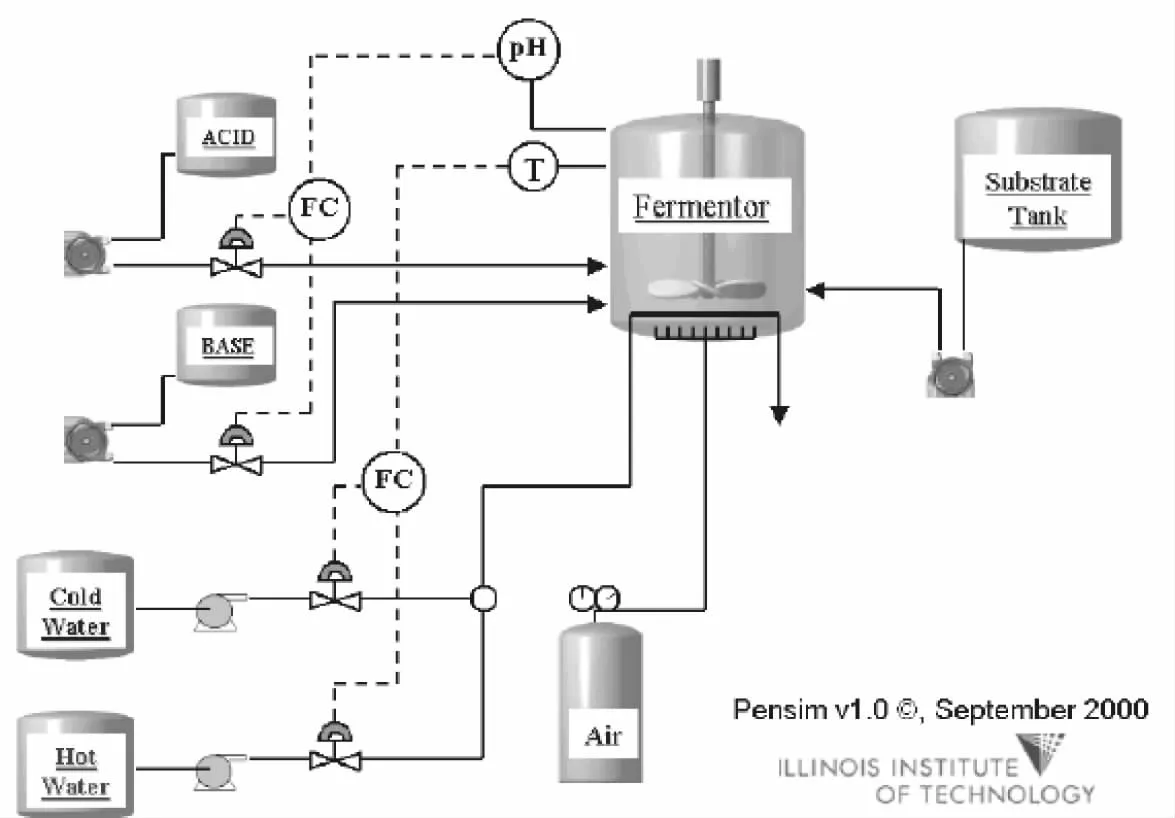
图1 Pensim仿真平台

检查各点是否超过控制限，若超过T2和SPE控制限，则发现故障，则说明该点出现故障；若没有超过控制限，则该批次数据正常.

2 基于MPCA的故障检测

模块的实验与分析

本文检测仿真数据从Pensim青霉素发酵仿真平台获得[6]，青霉素仿真平台如图1所示.

2.1 MPCA的数据预处理与建模

故障情况图中每个变量的说明如表1所示.

(1)基于MPCA的数据预处理

对20批次训练的样本，按变量方向展开，获得各阶段的2维子数据矩阵，通过聚类分析算法，对20批次训练的样本进行阶段分类，得出4个阶段，对每一阶段数据矩阵进行标准化处理，消除因量纲差异所产生的不合理影响.

(2)基于MPCA的训练样本建模

对每一阶段的数据矩阵进行PCA建模，根据主元贡献率计算出所需主元个数，并分别计算T2和SPE控制限.

(3)基于MPCA的在线数据建模

求每阶段的均值与标准差，然后对所有在线建模数据进行实时分析进行建模标准化，使用PCA建模方法求得该点的T2和SPE值.

2.2 故障检测结果

图2给出MPCA建模方法对故障1(典型斜坡故障)的检测结果.故障设定在160-180时刻加入一个10%的斜坡故障.

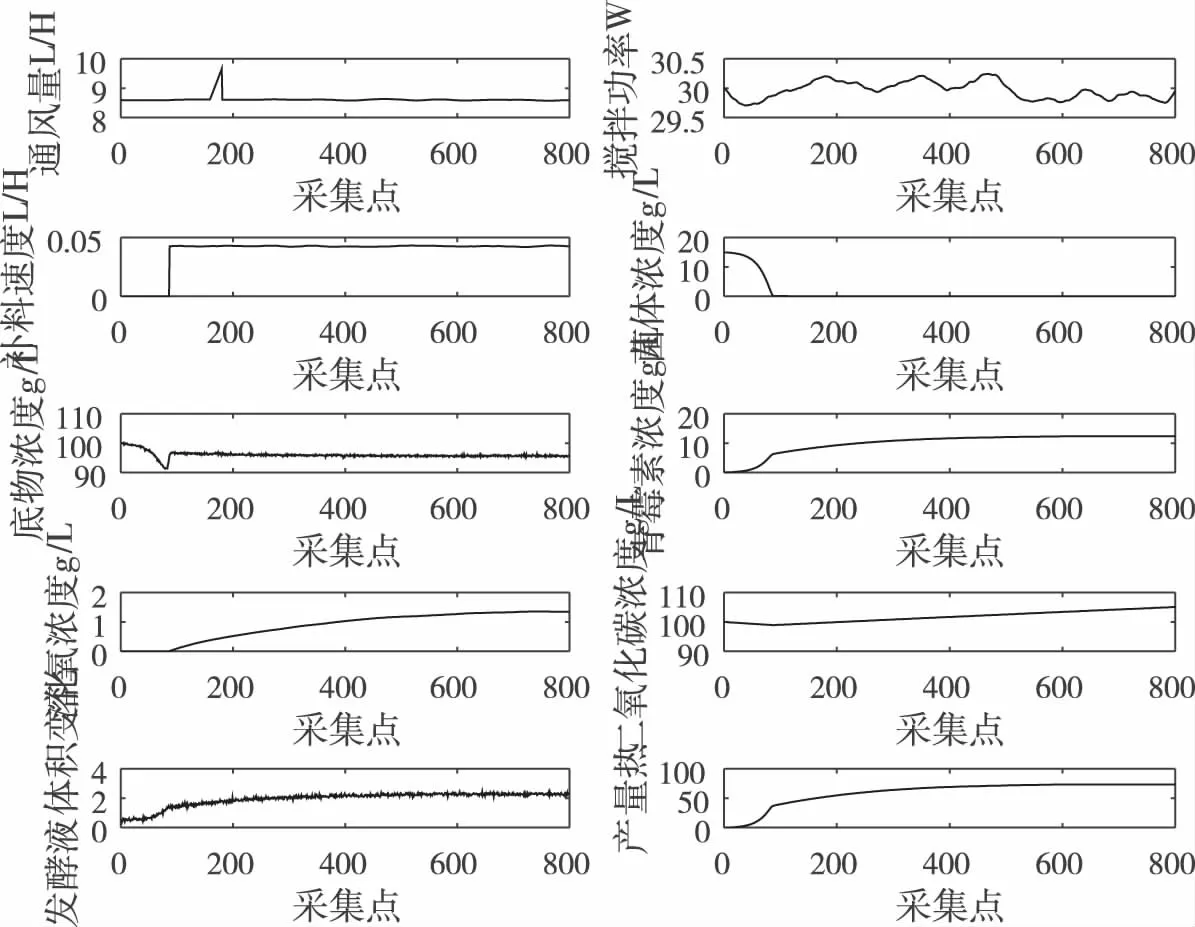
图2 故障1(斜坡故障)情况图

可以发现，MPCA建模方法SPE能检测到故障，同样可以检测到故障.通过检测故障后获得出现故障的时间点，然后在所有故障点上计算出对预测误差和(SPE)的贡献，这些变量最大可能会导致故障.在对故障1进行检测时，从如图3可以发现，出现故障时的点位于第170至180点之间，选择图3所示的四个检测点，计算出所有变量对SPE的贡献，可以看出故障起点在第170个点，进入故障期后，变量1的贡献逐渐增加，其他变量则逐渐减少.直到故障时段超出控制限最高的点(即第180个点)时，变量1的贡献值才达到最大，其他变量的贡献值几乎降到最低，在走出故障时段后，变量1的贡献值减小了，同时其他变量的贡献值也有所增加，这就可以说明变量1是引起故障的来源，而在文中分析变量1是引起故障的原因.在160-180点这一时间内，变量1(通风量)在此期间加入幅度5%的阶跃故障，这与最初设定的故障类型相一致，因此对故障的检测效果是有效的.

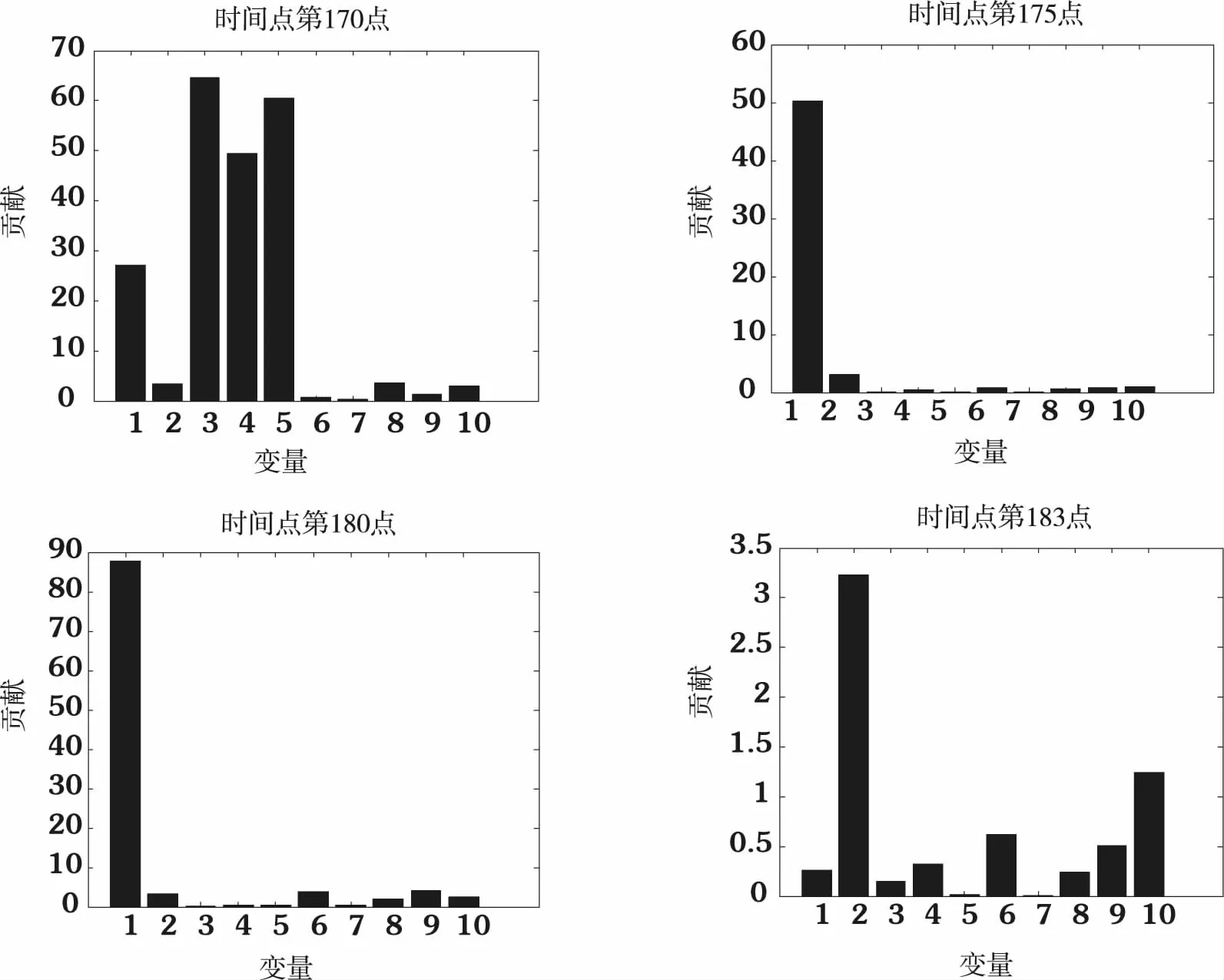
图3 故障一中各时间点各变量对SPE的贡献

3 总结与展望

以间歇过程为依据，引出了故障检测的概念，并从主元分析机理的角度，利用pensim平台模拟了青霉素的发酵过程.最后，MPCA建模检测了基于马氏距离的K-means聚类划分的子时段，并进行实验测试和评估.仿真结果可证明本文提出方法的有效性.