基于BP神经网络的管网漏失定位研究—以H市为例

王书盛 吴永强*

(1.河北建筑工程学院市政与环境工程系，河北 张家口075000；2.河北省水质工程与水资源综合利用重点实验室,河北 张家口 075000)

0 引 言

随着城市规模的不断扩大，城镇人口的不断增多，供水管网作为重要的基础设施，在向用户提供安全饮用水方面发挥着至关重要的作用，然而由于管网老化、施工质量不高及缺乏维护等原因，管网漏损、爆裂和渗漏现象时有发生，因此，有效、准确地检测供水管道的泄漏情况显得尤为重要.

目前，基于人工神经网络的模型在漏损预测研究方面有一定应用，Stephen等[1]介绍了一种利用人工神经网络分析传感器数据(流量和压力)的方法.采用静态和时滞两种神经结构对泄漏检测进行时间序列模式分类.在wachla等[2]提出的方法中，通过神经模糊分类器组来确定泄漏的位置.Ma等[3]提出了一种基于神经网络和图论的管道网络检测和定位方法.

本研究以H市某区为例，通过采集供水管网流量和压力的在线监测数据，以EPANET为平台建立水力模型，进行压力分析，并利用matlab建立BP神经网络模型进行漏损分析研究.

1 研究方法

1.1 BP神经网络

BP神经网络通常由三层组成:输入层，隐含层与输出层(如图1所示).通常输入层神经元的个数与特征数相关，输出层的个数与类别数相同，隐含层的层数与神经元数均可以自定义.BP(Back Propagation)神经网络的学习过程经历信号的正向传播与误差的反向传播两个过程.正向传播时，输入样本从输入层传入，经隐层逐层处理后，传向输出层.若输出层的实际输出与期望输出不符，则转向误差的反向传播阶段.误差的反向传播是将输出误差以某种形式通过隐含层向输入层反向传播，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据[4].

1.2 水力模型的建立

步骤1 数据收集与整理：在现有管网的SCADA智慧供水平台上收集各监测点的流量与压力，实地采集水厂水泵信息，包括水泵额定流量及扬程、效率以及清水池的水位和容积等信息.根据月用水量确定集中流量.

步骤2 简化管网，完善拓扑结构：首先简化DN300以下的管道和末梢节点，将末梢节点流量加在上一节点上，将两端相同的并联管道合成同一管道.

步骤3 用水规律的确定：城市居民用水量具有一定的规律性，从观测数据和统计数据可以看出用水量的规律性，根据用水规律的不同将用户大致分为4类(居民、医院、学校、工业)，每种用水类型选择多个典型用户进行监测，每1h记录一次累计流量，求得用水变化系数.

步骤4 EPANET建模：EPANET是由美国环境保护局在1994年创建的，主要用来模拟供水系统，其采用混合节点-环迭代法，简化了繁琐的环状网计算过程.本文采用一段时间内的数据分析结果进行建模，用Hazen-Williams公式计算管道内的压力损失，建立的网络模型.

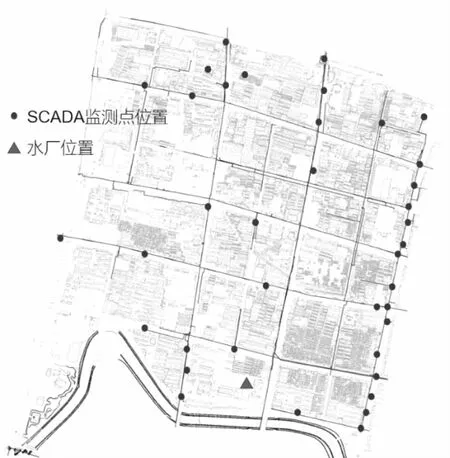
图2 EPANET中水厂与监测点位置图

1.3 BP神经网络模型的构建

1.3.1 训练样本

利用EPANET中的泄漏板块模拟管道漏损，并不能达到较理想的效果，本研究采用在漏损点安装短管的方法进行模拟(如图3所示)，短管横截面积模拟漏损断面，新增节点需水量模拟漏损流量，通过调节短管的参数进行泄漏点出水量与泄漏面积的模拟，并引入漏损面积比来表管道的泄漏水平：

(1)

式中：Ad表示泄漏处开口面积，m2；A0表示管道截面面积，m2.

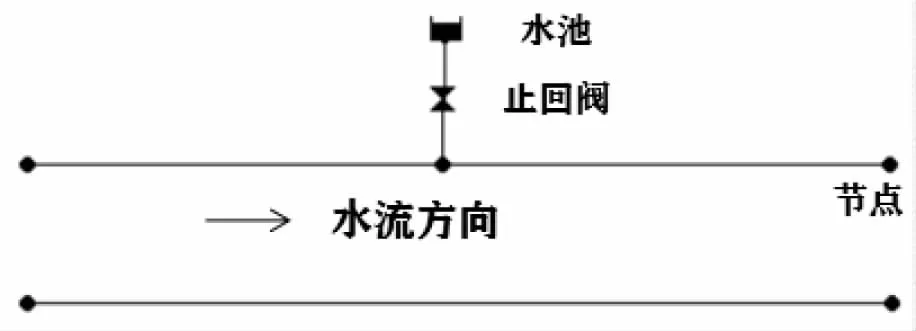
图3 漏损点设置

选取H市87条供水管道，包括主干管、支管，将各管道按照0.01、0.03、0.05的漏损面积比进行模拟，87条管道产生261组样本，为使漏损模拟更具真实性，模拟漏损点随机分布在不同的管段位置.系统随机选取80%的数据进行训练，剩下20%的数据进行漏损定位的验证.

1.3.2 数据预处理

在进行训练前，需要对数据进行归一化处理，即将数据映射到0到1之间，避免数据波动较大，对预测结果产生影响[5]，数据归一化公式：

(2)

式中：X为输入数据；maxX为输入数据的最大值；minX为输入数据最小值.

1.3.3 输入与输出层的确定

输入层为监测点的压力波动变化，输出层的神经元分别为漏损点坐标的x值与y值.隐含层节点数的确定是影响神经网络预测的重要参数.隐含层节点数过高容易造成过拟合的现象增加训练时间，影响精度；节点数过低，拟合精度受到影响导致精度不高.常用的隐含层节点数经验公式为：

(3)

式中n为输入层节点数，l为输出层节点数，a为常数，本文取5.隐含层个数对于预测结果的影响，当隐含层节点数为17时，模型训练集与预测集误差最小.此时训练集R2为0.94002，预测值R2为0.91728.

其他参数设置训练算法采用Levenberg-Marquardt，隐含层传递函数采用Tansig，输出层传递函数采用Purelin，误差函数为均方根误差MSE.最大迭代次数设置为200，最小误差值设为0.001，学习效率设为0.01，其他均为默认值.

2 案例分析

2.1 研究区域概况

H市位于我国华北平原地势平坦，海拔高度12～30 m，市区平均海拔在20 m左右，服务面积500多km2，服务人口61.07万余人，总水表户15万户，目前主要供水水厂为一水厂，日供水规模为10.7万t/d，水厂设置5台水泵，水泵性能参数为流量Q=2970 m3/h，扬程H=42 m，配用功率450 kw，转速990 r/min，日常工况下常开1～2台.H市主要以河流、铁路、分公司管理范围为边界，将供水管网分为9大管理区域，本研究主要研究区域为H市某区，其产销差居高不下，漏损的原因和漏损重点区域无法准确判断，对后续的诊断和治理工作造成极大困难.

2.2 BP神经网络预测结果与分析

当管段发生泄漏时，管网中的监测点的压力会发生变化，根据数值和变化范围反映管网整体运行情况，并根据压力变化确定漏损点位置.图4、5结果显示，横坐标训练的总回归值约为0.99，RMSE=103.5，纵坐标训练的总回归值约为0.99，RMSE=36.26，拟合点大多分布在直线上，表明漏损位置与监测点压力之间的预测精度很高，该BP神经网络漏损定位模型的精度满足要求.

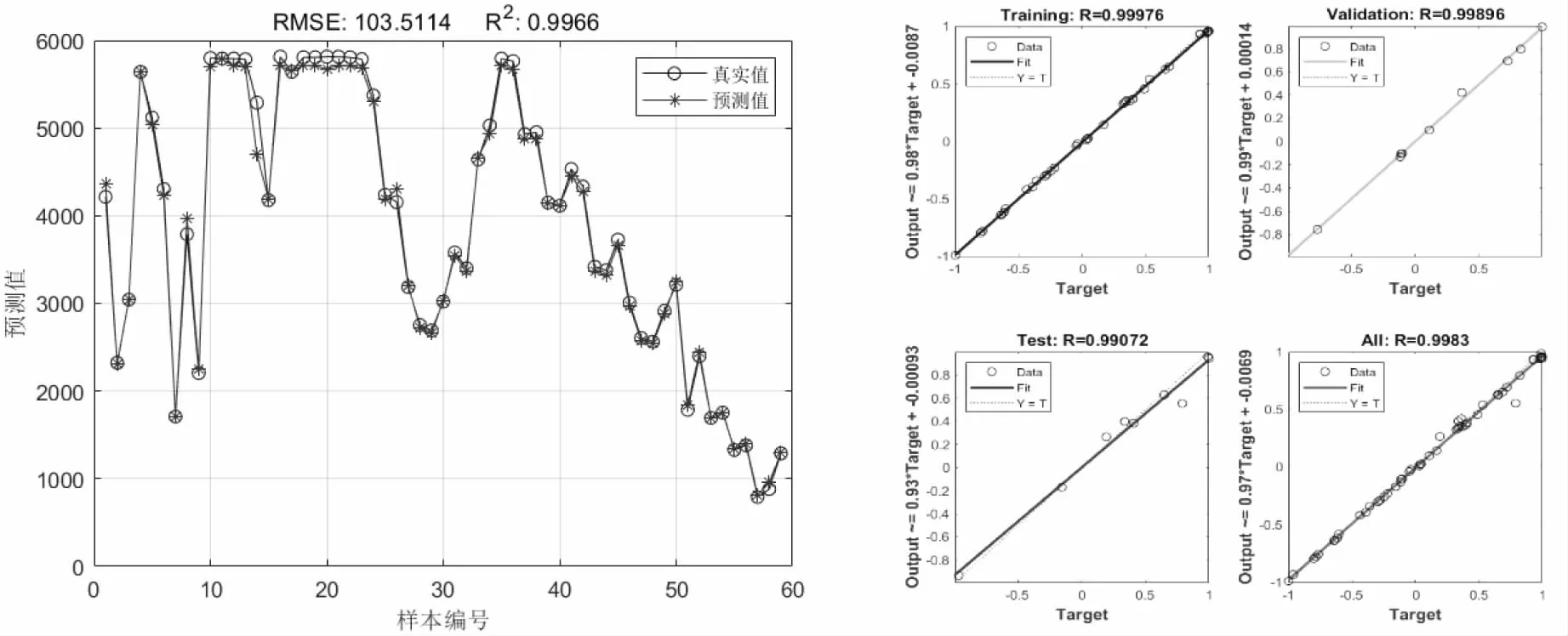
图4 Ka=0.01时横坐标预测结果

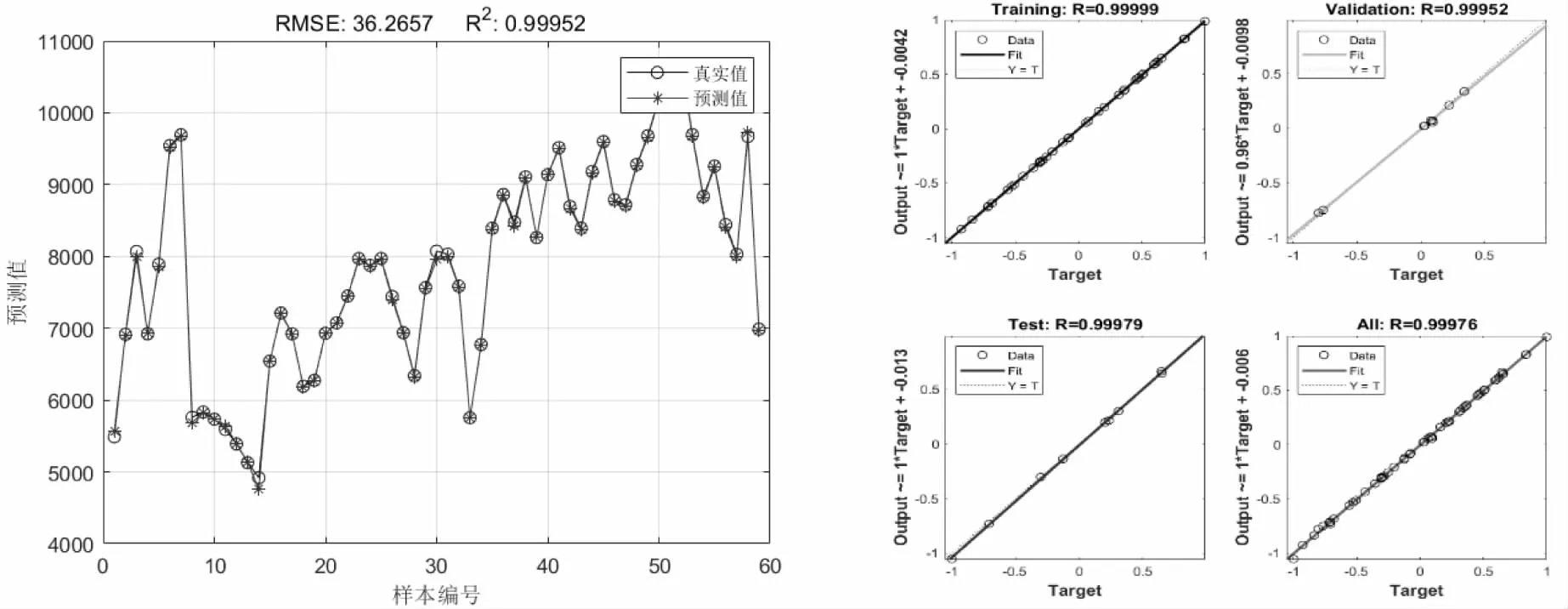
图5 Ka=0.01时纵坐标预测结果

本文通过对漏损数据的训练，利用BP神经网络建立供水瞬态压力变化与漏损点位置之间的线性变化，利用漏损数据库中的随机14组数据进行验证，检验模型的准确度，训练结果如图6、7所示.图6结果显示，就整体而言BP神经网络预测值与真实值的变化曲线基本吻合，可见数据拟合程度较好，漏损定位效果较为理想，当Ka=0.01时，真实值与预测值数据曲线基本重合.当Ka=0.03与当Ka=0.05时，预测曲线与真实值存在较小偏差.

图7为横纵坐标相对误差值，当Ka=0.01时真实值与预测值横纵坐标相对误差分别是1.61%和0.44%；当Ka=0.03时，相对误差分别为8.53%和7.24%；当Ka=0.05时，相对误差为7.82%和3.68%，纵坐标的相对误差小于横坐标，结果显示本文采用的定位方法对于纵坐标的灵敏度较高，定位也较为准确.后半段曲线相对平稳且相对误差较小，此时的管段大多是位于管网下游DN300的管段，说明模型对于支管漏损定位较为稳定且准确率高.

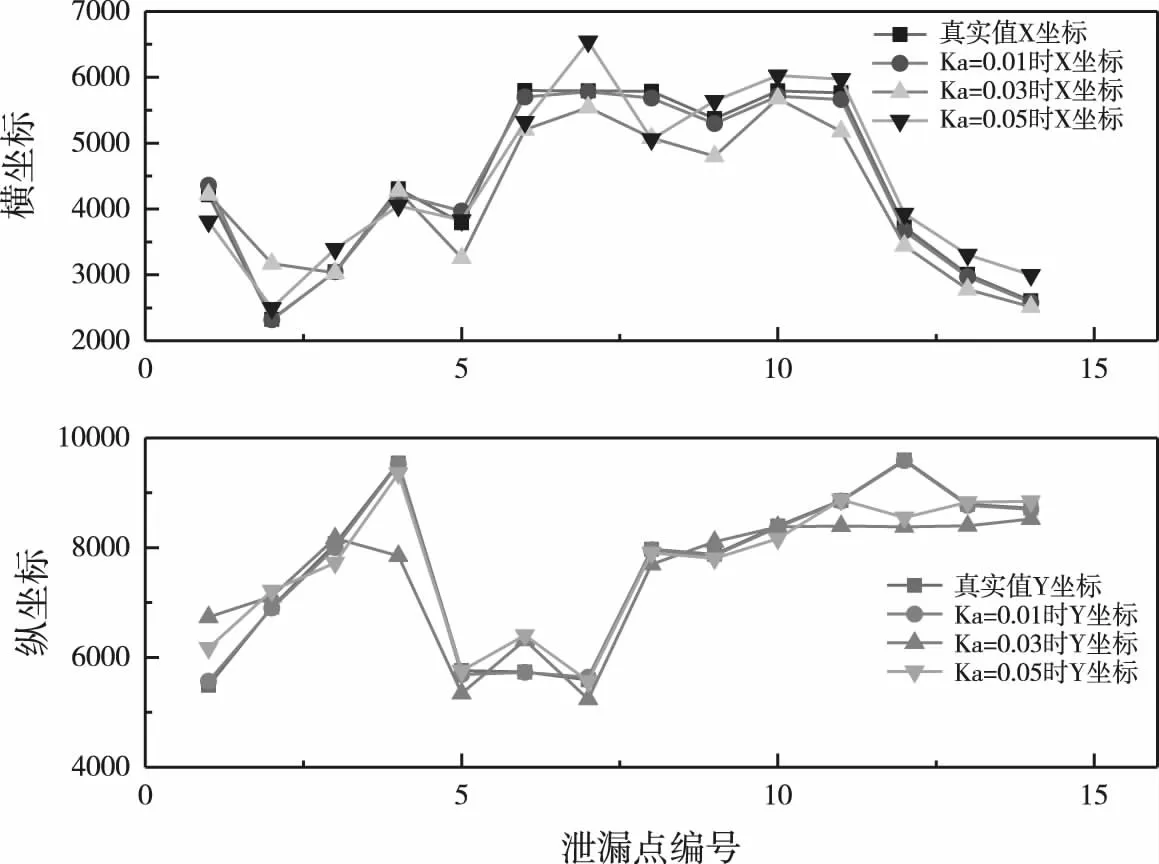
图6 BP神经预测结果

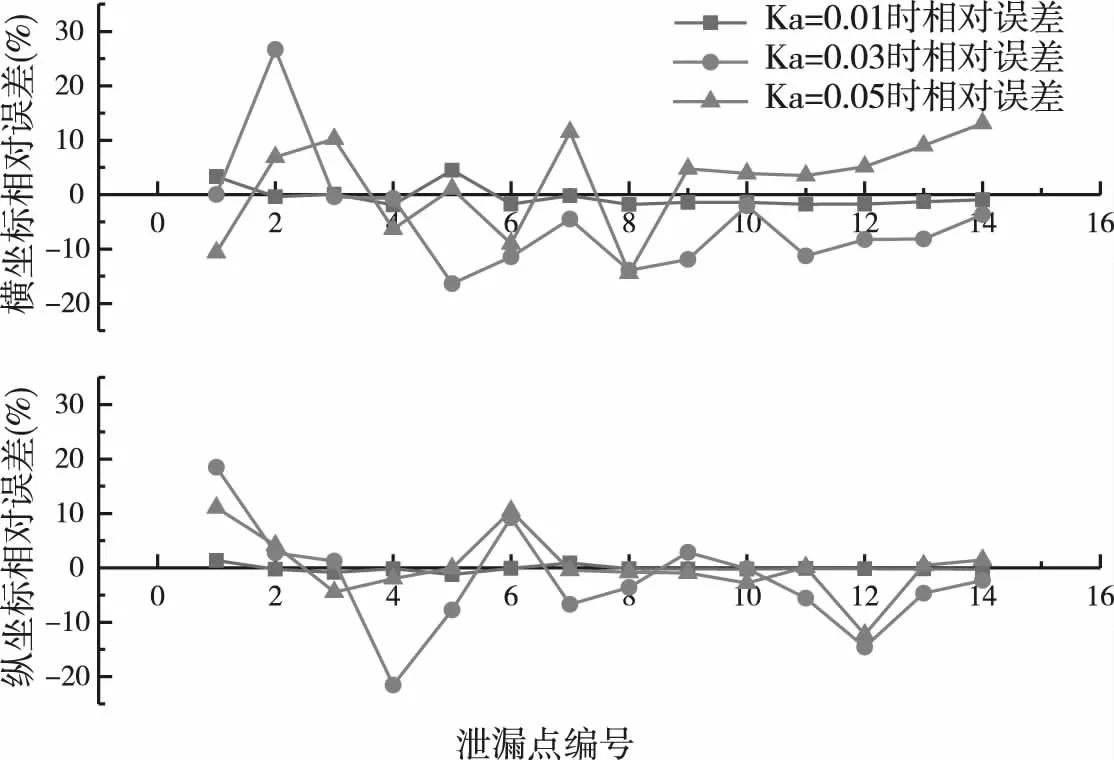
图7 相对误差图

表1为漏损定位部分结果，结果表明，模型具有较好的预测能力.当Ka=0.01时，漏损定位效果最好，预测点距离漏损点最近的距离为19.71 m，最远距离为192.29 m，平均偏差为78.1 m，50%预测样本的偏差距离在50 m左右.当泄漏量扩大时，模型的定位精度有所下降，Ka=0.03时平均距离为674 m，Ka=0.05时平均距离469.2 m.除去个别异常值外，80%预测误差能维持在300～400 m左右，对于实际工程中的漏损点的排查具有指导意义.可见所构建的神经网络基本满足对于漏损点的定位要求.

同一管段不同泄漏面积相比，定位效果也不同，漏损量越大定位效果越差；本文中对管径DN300的管段漏损定位效果最好，优于主干管与大管径管段.原因是当小管径管段发生泄漏时，附近节点的压降较其他节点更为明显，而当主干管漏损时或漏损量加大时，管网节点压力普遍下降，且下降幅度与泄漏点附近节点的下降幅度差别不大，导致模型无法根据压力变化准确定位.

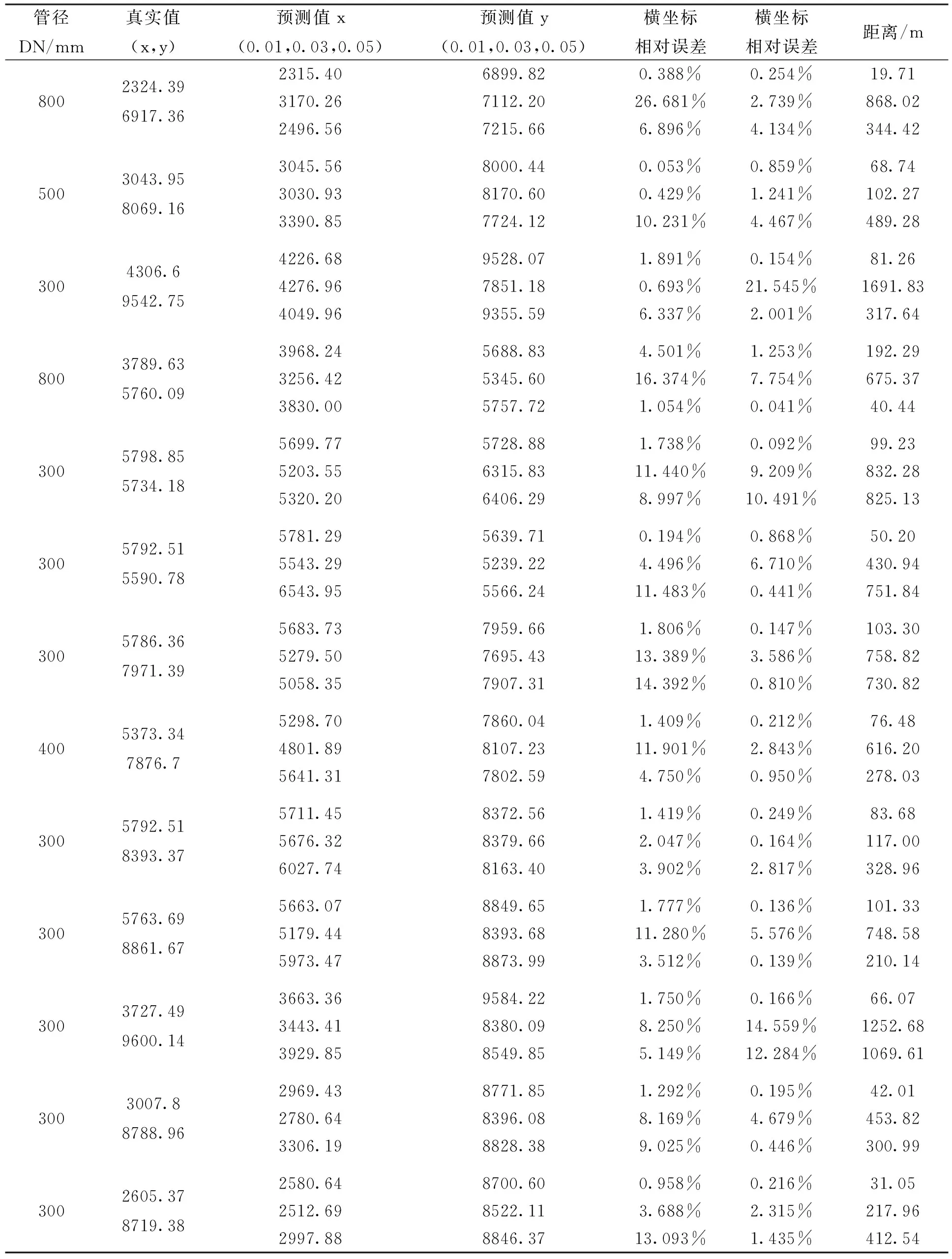
表1 漏损定位部分结果展示

3 结 论

(1)正常工况下，管网节点压力随着当地用水习惯的变化呈现出一定的用水趋势.当管道发生泄漏时，距离泄漏点最近的监测点受到的影响最大.当主干管或干管发生泄漏时，整个管网的监测点压力会普遍下降，且下降幅度大致相同.

(2)本文模型对于漏损面积比为Ka=0.01时的漏损及支管漏损具有较高的定位精度.横纵坐标误差分别为1.61%和0.44%，平均偏移距离为78.1米.同一管段，不同的漏损面积比，随着漏损量的加大，漏损定位精度有所下降.且模型对于小流量的漏损及支管漏损的定位效果较好，模型更加精确，数据拟合度高达0.9966，这为管网漏损定位提供新方法.