阀控非对称缸系统特性分析与位置控制研究
孙家庆,张培珍,曹秀芳,翟丽娟,韩宁
(南京晨光集团有限责任公司,江苏南京 210006)
0 前言
针对电液位置伺服系统,国内外学者展开了一系列研究。阀控缸系统(包括对称阀、非对称阀控制对称缸,对称阀、非对称阀控制非对称缸)在工程中广泛应用,为提高阀控缸系统的控制精度,必须要得到阀控缸系统的准确数学模型。部分学者采用功率键合图的方法进行建模,并分析了系统的非线性特性。吕云嵩和江桂云等从频域特性的角度建立阀控缸系统的非线性数学模型。孟亚东和张尚盈等采用机制建模的方法,建立了阀控缸系统的传递函数,并采用仿真手段验证了模型的有效性。杨庆俊等采用工作点线性化方法,建立了阀控缸系统数学模型。采用传统的方式建立受控对象动力学模型时,常出现模型精度不高甚至难以建立系统模型的问题,这极大地限制了各种控制理论的应用和控制性能的提高。因此,也有学者采用系统辨识的方法对阀控缸系统进行模型辨识,得到准确的数学模型。
除了系统精准建模的问题,阀控缸系统仍然面临非线性鲁棒控制问题。目前,针对阀控缸系统的非线性控制,国内外学者做了大量工作。部分学者采用PID的控制方法解决阀控缸非线性系统的鲁棒控制问题。YAO和柳波等人针对阀控缸系统模型不确定性和非线性问题,提出了自适应鲁棒控制器。YU等针对阀控缸系统模型不确定性和非线性的问题,提出了基于Backstepping的鲁棒状态反馈控制器。目前很多学者也将神经网络与控制理论相结合,解决阀控缸系统非线性补偿的问题。
因此,本文作者基于阀控非对称缸液压系统原理,结合系统辨识的方法,建立阀控非对称缸的非线性数学模型,结合时域、频域分析方法,分析阀控非对称缸系统的特性,提出基于位置前馈和双PID控制方法补偿非对称缸位置控制问题。
1 阀控缸系统原理与数学模型
1.1 阀控缸系统原理
阀控缸系统的原理如图1所示:液压缸输出的位移由位移传感器测出并反馈到控制模块,测控平台输出给定信号到控制模块,给定信号与采集信号的差值通过控制模块输入到比例换向阀中,以进一步控制液压缸的输出位移。
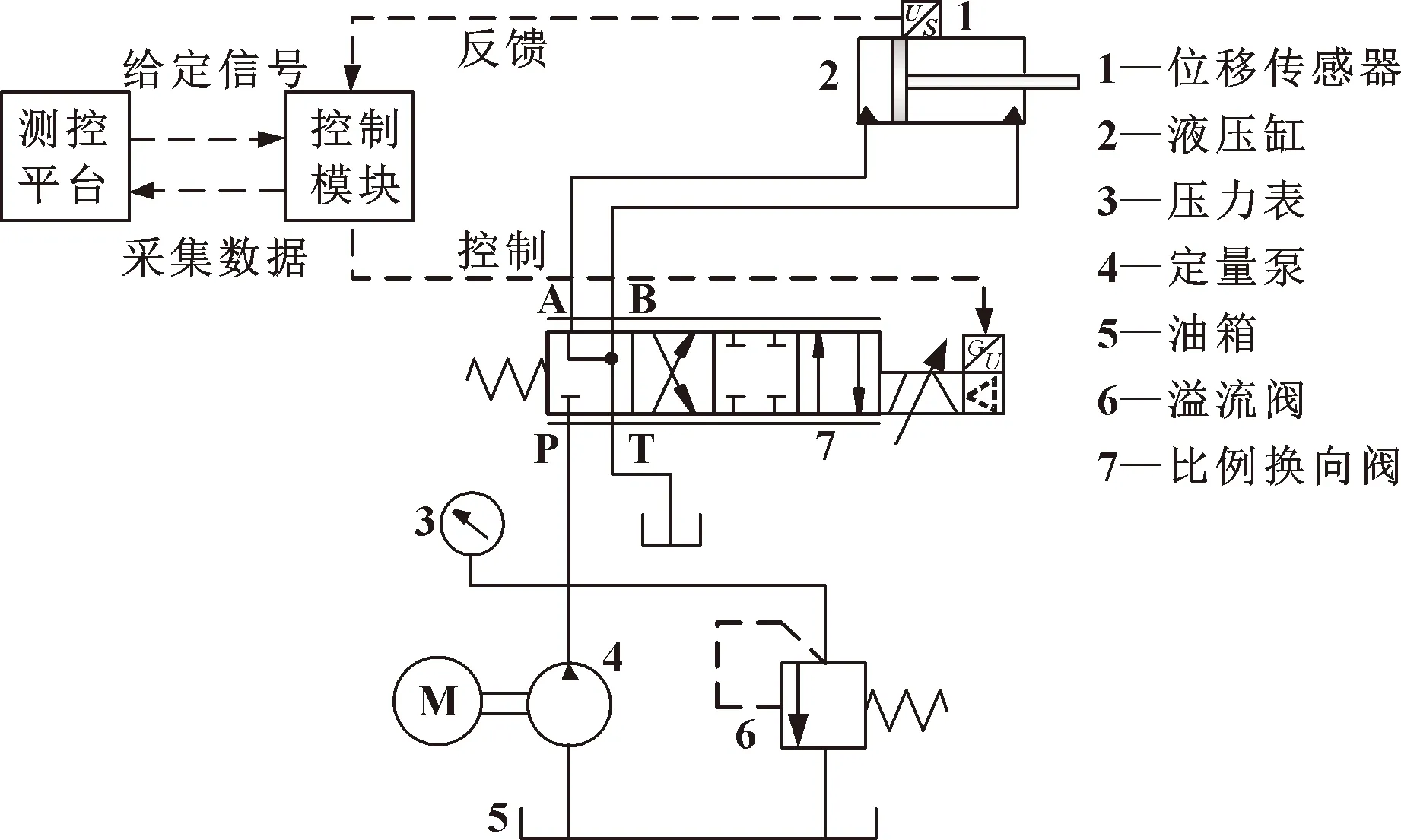
图1 阀控缸系统原理
1.2 数学模型
比例换向阀的流量方程为
()=()-()
(1)
式中:()为比例换向阀流量,L/min;为比例换向阀流量增益;()为比例换向阀阀芯位移,m;为比例换向阀的流量-压力系数;()为负载压降,MPa。
液压缸流量连续性方程为
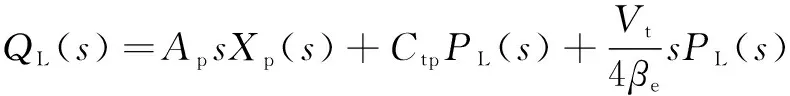
(2)
式中:为液压缸活塞有效面积,m;()为活塞位移,m;为液压缸总泄漏系数;为液压缸总压缩容积,m;为有效体积弹性模量。
液压缸和负载的力平衡方程为
()=()+()+()+()
(3)
式中:为活塞及负载折算到活塞上的总质量,kg;为活塞及负载的黏性阻尼系数,N·s/m;()为作用在活塞上的任意外负载,N。
由式(1)—式(3)可得阀控缸系统框图,如图2所示。
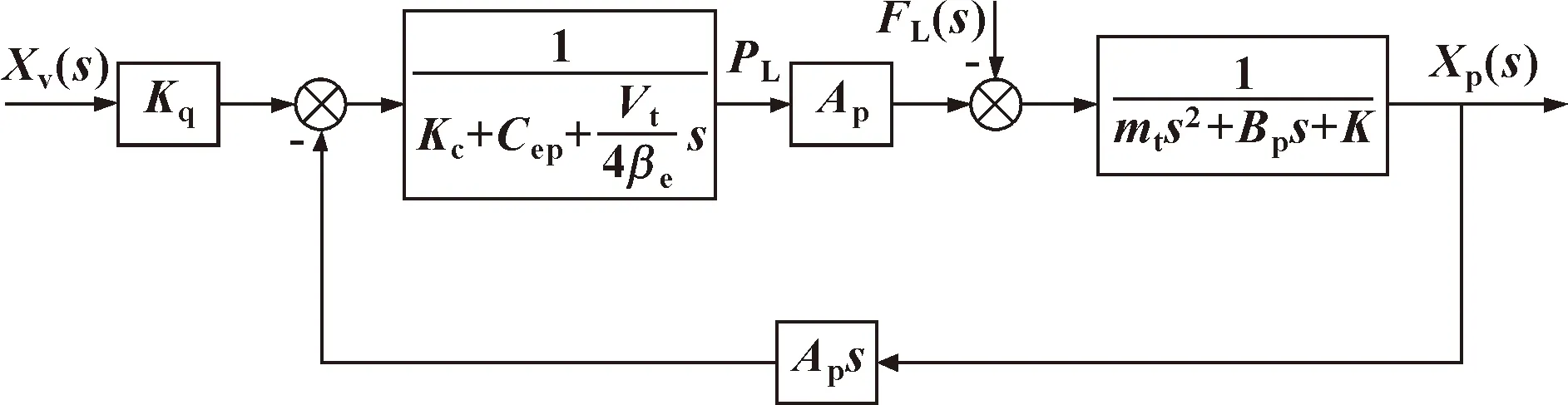
图2 阀控缸系统框图
由式(1)—式(3)或通过图2所示的阀控缸系统框图可得阀芯位移和外负载同时作用时液压缸活塞的总输出位移为

(4)
式中:为总流量-压力系数,=+。


(5)
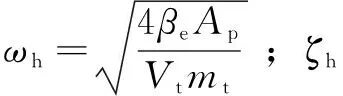
所以,对输入的传递函数(阀控缸系统的开环传递函数)为

(6)
对干扰输入的传递函数为

(7)
该阀控缸液压系统输入的是一个恒定压力值, 其传递函数为

(8)
2 阀控缸系统闭环传递函数辨识
2.1 时域特性辨识
文中采用实验法求取阀控缸系统数学模型,基于液压实验室的力士乐液压教学平台和测控平台完成,实验平台实物如图3所示。其中,液压教学平台主要用于搭建液压系统和电控系统,测控平台主要用于输出给定信号和采集液压缸的位移。

图3 阀控缸系统实验平台
测控平台硬件采用NI板卡,软件采用LabVIEW,该软件是一种程序开发环境,由美国某公司研制开发,是一个标准的数据采集和仪器控制软件。程序面板及对应的前视面板如图4所示。

图4 LabVIEW面板
依托上述实验平台,结合上述对阀控缸系统特性的分析,引入PID调节器,调整PID调节器中的比例系数,观察液压缸的输出,对系统进行参数辨识。阀控缸系统位置控制框图如图5所示。

图5 阀控缸系统位置控制框图

图6 阀控缸系统阶跃响应
采用MATLAB软件,利用上述实验数据、系统模型和如下程序指令,得到如图7所示的辨识结果。

图7 辨识结果
》y=bianshi.Y(1,7).Data;y1=y-0.5;x=bianshi.Y(1,1).Data;x1=x-0.5;
dry =iddata(y1(1000:7001)′,x1(1000:7001)′,0.001);
figure(1);plot(dry);
zf=idfilt(dry,[0,500],8,5);
figure(3);plot(zf);
[zr]=idresamp(zf,1,8,0.1);
蒋介石在1932年发表的一篇讲话中强调:“总理更进一步用‘知难行易’的学说,要来启发中国的民族精神,并用来实行他的革命主义。总理的意思,就是说:你们既知道三民主义和国民革命是好的,那你就只要照我的‘革命方略’去做,照我的三民主义去行,就一定能够完成革命了。所以总理常讲:‘你们一般党员只要照我所讲的话实在去行就好了,不要再去求另外的知。’他的意思即是:良知是我们大家所固有的,故不必另外再去求知,若说要求学问的知识完全,就要用许多时间更是不易,求‘知’既是不易,即是很难,后知后觉,以及不知不觉的人们,只是跟着先知先觉的人们去行,就可以节省时间,完成革命,因为跟着去‘行’是很容易的。”㉚
figure(4);plot(zr);
nns=[4 2 3];m=arx(zr,nns);
figure(5);bode(m);figure(6);plot(m);
compare(m,zr);
iscstbinstalled=license(′test′,′control_toolbox′)
&& (exist(′bode′,′file′)==2);
if iscstbinstalled
tfm = tf(m,′m′)%′m′ for ′measured′.
end
sys=d2c(tfm,′tustin′)
figure(7);bode(sys);
grid on;
figure(8);pzmap(sys);
考察阀控缸闭环系统固有特性,取控制器比例系数为1时,系统输入为阶跃信号,通过MATLAB程序结合实验数据对阀控缸系统进行辨识,得到阀控缸系统的传递函数为

(9)
由图7可知:辨识精度为97.66%,辨识得到阀控缸系统闭环传递函数的惯性环节转折频率为106 rad/s,该频率对应开环增益,称为速度放大系数,表征了阀对缸速度控制的灵敏度,该系数直接影响阀控缸系统的快速性、稳定性和准确性。Bode图幅频特性斜率-20 dB与-60 dB转折点对应二阶振荡环节的转折频率,该频率表征了阀控缸系统的二阶振荡环节的固有频率为421 rad/s,该频率处幅频特性曲线的谐振峰值表征了阀控缸系统的阻尼比,阀控缸系统二阶振荡环节阻尼比为0.486。
2.2 频域特性辨识
由式(6)可知,阀控缸伺服系统可以简化成典型的比例环节、积分环节和二阶振荡环节的乘积。对阀控缸位置伺服控制系统进行频率响应实验,控制器=1、=0,给定频率从10 rad/s变化到650 rad/s,分别计算每一个频率点的幅值比和相位差,描出Bode图如图8所示。位置反馈通道设置转折频率为0.5 Hz的惯性环节,在高频给定信号时采集数据反映的是系统开环特性。

图8 频域特性辨识Bode图
穿越频率=94 rad/s对应开环增益,称为速度放大系数,表征了阀对液压缸速度控制的灵敏度,该系数直接影响阀控缸系统的快速性、稳定性和准确性。
Bode图幅频特性斜率-20 dB与-60 dB转折点对应二阶振荡环节的转折频率,该频率表征了阀控缸系统的固有频率为473 rad/s,该频率处幅频特性曲线的谐振峰值表征了阀控缸系统的阻尼比。
3 阀控缸系统特性分析
3.1 稳定性分析
由式(9)可知,系统的特征方程为
+5153+2206×10+1879×10=0
(10)
式(10)中各项均为正。列出劳斯列表为

劳斯列表第一列各项符号皆相同且均为正号,系统稳定。
3.2 快速性分析
采用MATLAB软件编程,绘制式(9)所示系统传递函数的Bode图,如图9所示。

图9 阀控缸系统闭环Bode图
由图9可知:系统的截止频率=62 rad/s、带宽0≤≤62 rad/s,带宽偏小,带宽表征了系统响应的快速性,所以系统的快速性需要进一步改善。
3.3 准确性分析
由式(6)可知,系统开环传递函数中积分环节的个数为1,所以系统为I型系统,该系统在阶跃输入的情况下没有稳态误差。
4 阀控非对称缸位置控制研究
4.1 控制思想
本文作者采用位置前馈和双PID的控制方法来补偿非对称缸位置控制,控制思想如图10所示。
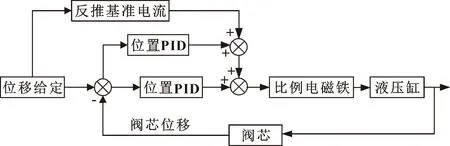
图10 位置控制思想
文中所涉及的位置闭环控制主要包含两个环节:位置闭环、基准电流前馈。指令位移与采集阀芯位移作差,该偏差经过PID后与基准电流叠加。根据阀芯受力平衡,得到指令位移下对应的电流,以前馈环节的形式加到位置闭环的输出端,即位置闭环PID控制之后,该电流作为所需位移的基准电流。由于实际情况下存在摩擦力、液压缸非对称等因素,理论推导的关系并不能反映实际情况,位置PID中的积分环节用来补偿这部分非线性因素的影响。
4.2 控制效果
为验证所提出的控制策略的有效性,结合上述对阀控缸系统特性的分析,在保证系统具有足够稳定裕量的前提下,尽量提高系统的动态响应速度。基于如图3所示的实验平台进行研究,系统的响应如图11所示。可知:在保证系统稳定裕量的前提下,随着比例系数的增加,最大超调量增大,系统的快速性明显提升,稳态误差减小,即系统的控制精度明显提升。系统超调量增加,导致系统的稳定性有所下降,但仍满足系统稳定性的要求。
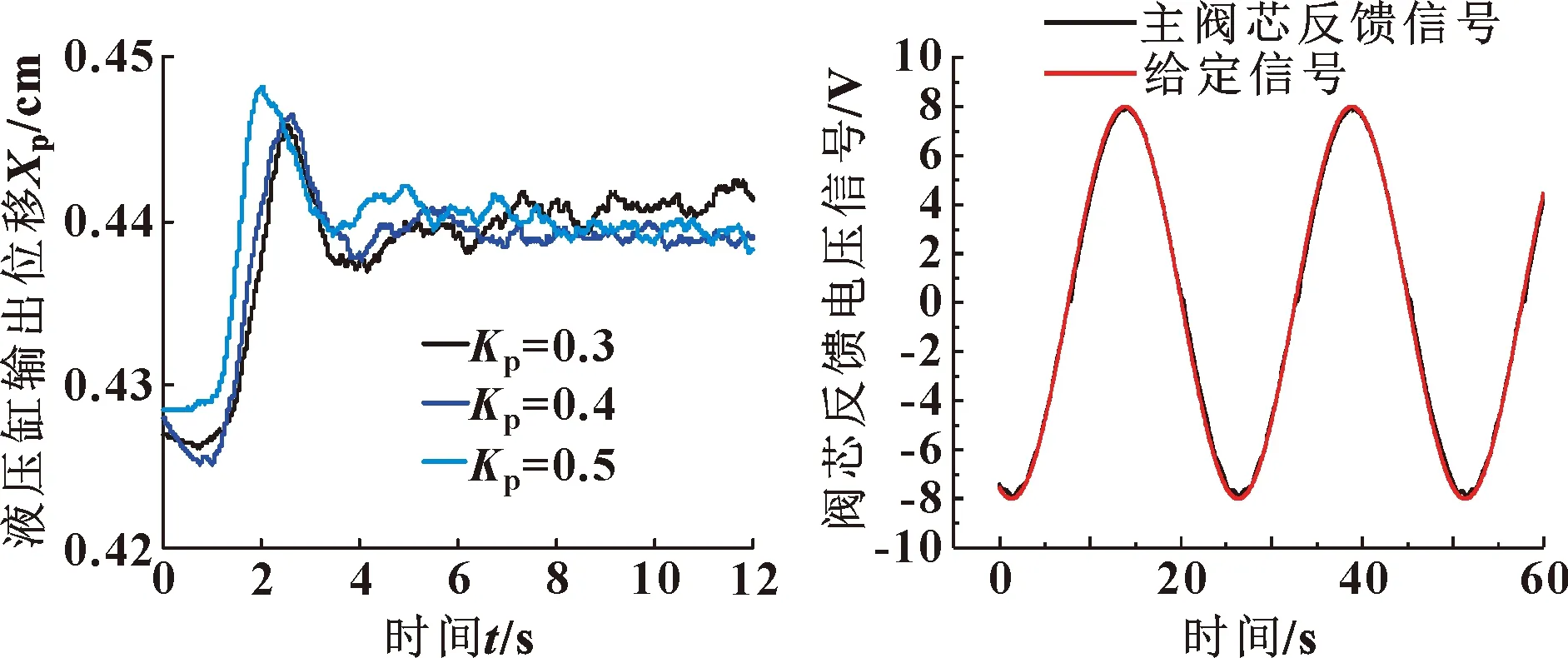
图11 阀控缸系统PI控制系统响应 图12 正弦响应
为验证该控制系统在周期为25 s的正弦信号作用下的响应,采集液压缸位移传感器输出的电压,如图12所示。
由图12可以看出:系统准确快速地跟踪了给定信号,且误差在允许范围内。
5 结论
通过上述研究结果,可以得出如下结论:
(1)通过时域和频域的辨识方法,得到系统准确的传递函数,并分析了系统的稳定性、快速性和准确性。
(2)针对阀控非对缸位置控制系统,提出了一种指令基准前馈和双位置PID的控制策略。在保证系统稳定裕量的前提下,该系统可实现较高精度的位置控制。

