计入波纹度的柔性角接触球轴承振动特性研究

王龙滨，吴邦伟，李志强，陈勇

(1.东营市商务局,山东东营 257091；2.济南大学机械工程学院,山东济南 250024)

0 前言

角接触球轴承是机械系统的关键基本部件，当角接触球轴承的部件出现制造误差和柔性变形时，轴承内部载荷会发生非线性变化，从而产生异常振动和疲劳损伤。因此，研究具有制造误差的角接触球轴承的振动具有重要意义。

国内外研究学者对轴承振动开展了许多研究，LIU等研究了柔性圈和柔性滚子对柔性圆柱滚子轴承振动的影响。VIITALA分析了内圈圆度对转子亚临界响应的影响。刘静等人研究了计入内圈表面波纹度的圆锥滚子振动模型，分析了表面波纹度幅值和阶次对圆锥滚子轴承的振动特性。余光伟等研究了波纹度波数与某三自由度深沟球轴承振动特性的影响规律。夏玉磊等研究了弹性支承的SDF圆柱滚子轴承振动的耦合动力学模型，分析圆柱滚子在工作过程中动态特性的影响。康锋等人针对薄壁轴承-转子系统的振动特性，分析了内外圈波纹度等因素对轴承振动的影响规律。李静等人研究了航空发动机双转子系统的振动特性，结果表明轴承波纹度的影响加大了双转子系统的振动特性。周元坤等研究了载荷作用下轴承的几何协调方程，提出了几何协调方程与载荷作用下的迭代算法，在此基础上研究了内圈圆度误差阶次对轴承振动的影响规律。

虽然对滚动轴承动力学进行了各种研究，但仅有少数学者对具有制造误差的柔性圆柱滚子轴承动力学进行了研究。此外，对于具有波纹度的柔性角接触球轴承的动力学研究还很少。因此，本文作者提出了一种计入波纹度的柔性角接触球轴承动力学模型，该模型考虑了润滑和波纹度对轴承动力学的影响。为了测试轴承振动，搭建了轴承振动实验台，验证了动力学模型的正确性，研究结果对阐明轴承失效机制、提高轴承制造精度具有一定的指导意义。

1 角接触球轴承的振动模型

角接触球轴承模型如图1所示，可以看出：柔性角接触球轴承圈和刚性角接触球轴承圈之间的区别，与轴承连接的轴是刚性的。由于轮廓波纹度的存在，轴承内部载荷会在振动信号中产生边带频率和峰值。润滑油和外部负载也会影响角接触球轴承的振动特性。因此，柔性角接触球轴承和刚性角接触球轴承之间的振动是不同的，文中将对具有波纹度的柔性角接触球轴承和刚性角接触球轴承振动进行研究。

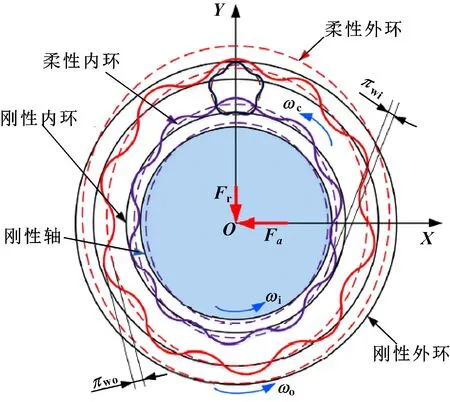
图1 具有轮廓波纹度的角接触球轴承模型

1.1 轴承油膜刚度计算方法

根据文献[11]提出的等温条件下弹性流体润滑(EHL)油膜厚度修正方程，点接触量纲一化中心油膜厚度如式(1)：

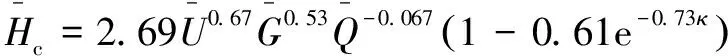
(1)

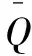
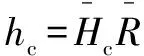
(2)

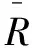
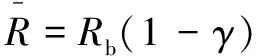
(3)

其中，为

(4)

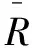
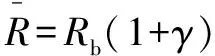
(5)

滚子与圈之间的油膜刚度定义为

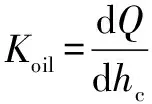
(6)

式中:为接触负载。因此，滚子与圈之间的综合接触刚度描述为

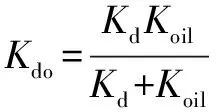
(7)

则两圈与滚子之间的总接触刚度为

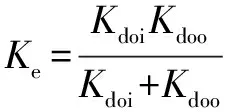
(8)

其中:和分别为滚子与内圈，以及滚子与外圈之间的接触刚度。

1.2 滚子接触力的计算方法

设第个滚子与内外圈之间的回弹力为，与接触弹性变形的关系为

=

(9)

式中:为载荷变形指标，对于点接触，=1.5;为滚子与圈之间的等效接触刚度。为第个球在角度位置处的总接触变形，表示为

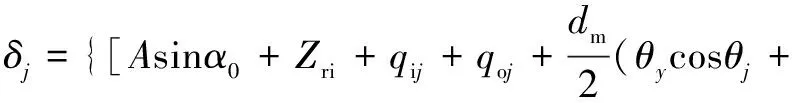
sin)]+(cos+cos+cos+sin)+

i+o}12-++1+2

(10)

其中:i和o分别为内圈和外圈上的轴向波纹度，可以表示为

(11)

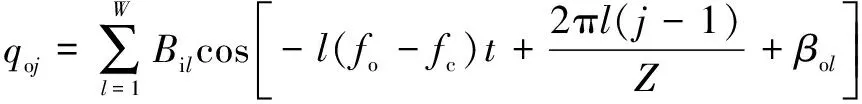
(12)

此外，i和o分别为内圈和外圈的径向波纹度，可以表示为

(13)

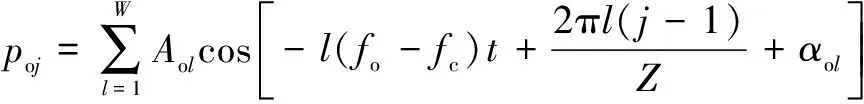
(14)

其中:1和2分别为滚子与两圈接触点的中心油膜厚度;表示为

=+-

(15)

其中:和分别为内圈和外圈通道的曲率半径;和分别为内圈和转轴在和方向的位移；为滚子直径；为节圆直径；为预紧作用下内圈和转轴在方向的位移，并由下式给出：

=sin-

(16)

其中：为滚子与圈在预紧力作用下的接触变形，可以表示为

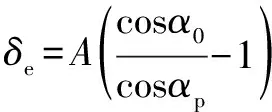
(17)

是预紧力作用下内圈和转轴在方向上的位移，表示为

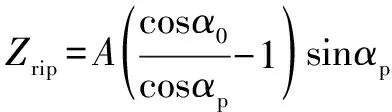
(18)

其中:为初始接触角;是预紧力作用下的接触角，预紧力和可以由下式得到：

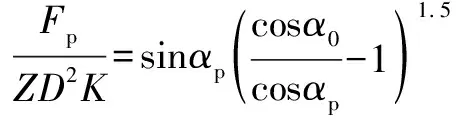
(19)

另外，在任何角度位置处的第个滚子被描述为

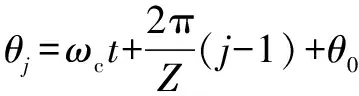
(20)

其中:为第一个滚子的初始角速度位置;为滚子数;为保持架的角速度。轴向载荷为

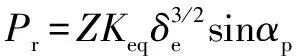
(21)

第个滚子接触角可以描述为

=

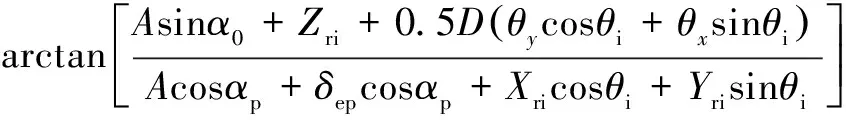
(22)

其中:、为转轴和内圈绕、轴的摆角位移。

1.3 接触力的计算方法

根据柔性圈变形计算方法，外圈的离心膨胀描述为

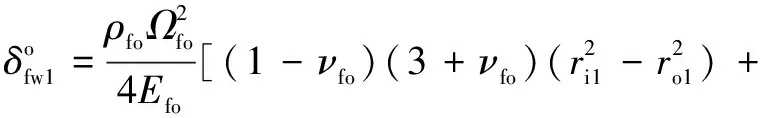
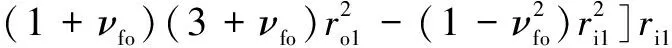
(23)

其中:是外圈转速;为外圈弹性模量;为外圈泊松比;为外圈密度;和分别为外圈的内径和外径。内圈的离心膨胀公式为

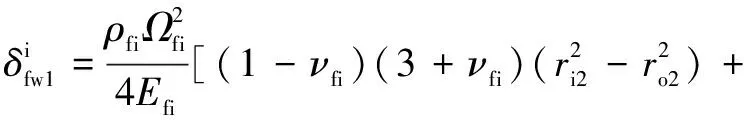
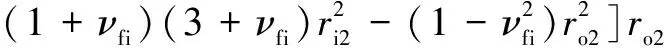
(24)

其中:为内圈密度;为内圈转速;为内圈弹性模量;为内圈泊松比;和分别为内圈的内径和外径。接触载荷作用下的滚子柔性变形为

()=()(+cos+cos2)

(25)

其中:()是作用在圈上的接触载荷;、、为刚度系数，其值可参考文献[15]中的方法计算。因此，柔性圈的变形可表示为

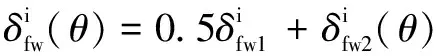
(26)

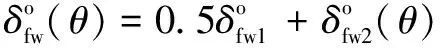
(27)

其中:上标i和o分别表示内圈和外圈。在任意角位置处的总接触变形描述为

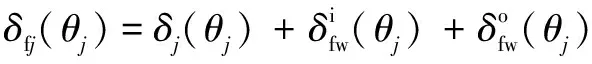
(28)

其中：为刚性圈在任意角位置处的总接触变形，因此滚子与柔性圈之间的接触力可由下式表示：

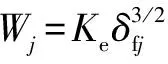
(29)

1.4 动力学方程

图2所示为角接触球轴承转子系统的动力学模型，图中h、h、h为圈体在、、三个方向上的刚度，h、h、h为圈体在、、三个方向上的阻尼。此研究在拉格朗日方程的基础上，建立考虑轴承润滑、轴承柔性变形和波纹度的角接触球轴承转子系统动力学方程：

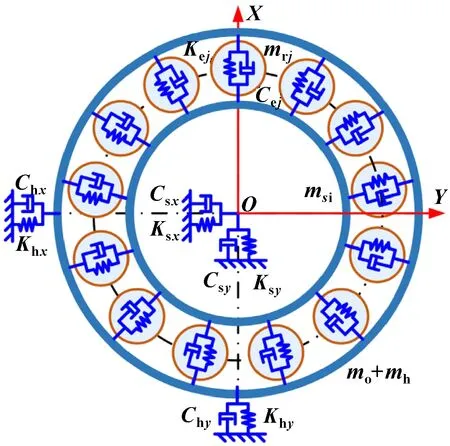
图2 角接触球轴承转子系统的动力学模型

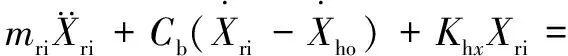
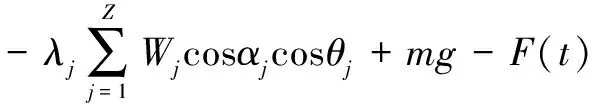
(30)

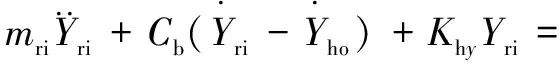
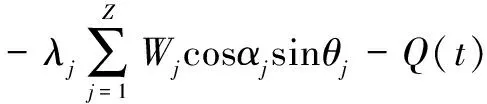
(31)

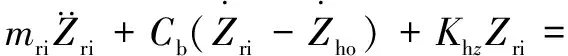
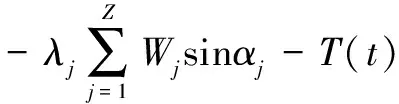
(32)

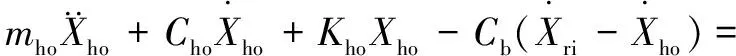
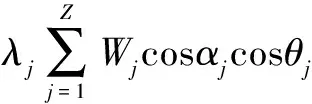
(33)

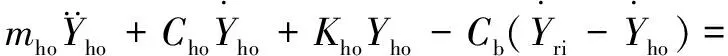
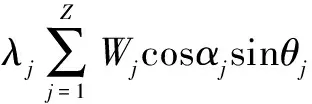
(34)

(35)

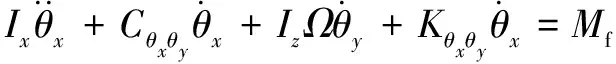
(36)

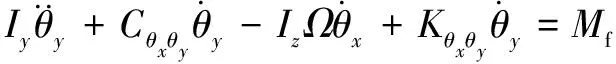
(37)

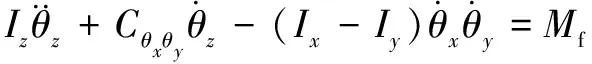
(38)

式中：、和分别为内圈和转轴在、、3个方向上的位移，、、分别为外圈在、、3个方向上的位移;和分别为内圈-转轴总质量和外圈-圈体总质量，和分别为轴承和圈体的阻尼系数；是重力加速度；、、分别为内圈-转轴绕、、轴的惯量；()、()、()分别是沿、、方向的外荷载。

2 计算结果与分析

采用四阶Runge-Kutta数值解法求解角接触球轴承的动力学方程，分析含有波纹度的柔性轴承的动载荷和振动。表1给出了不同波纹度阶数情况下的轴向和径向振动频率，主频率=1，谐波≥1。表2给出了不同波纹度阶数情况下的振动边带频率。当波纹度阶数大于滚子数时，表2中标记为“过大”，波纹度激励下的轴承振动频率由滚子和保持架旋转频率组成。角接触球轴承的几何参数如表3所示，轴承转速为18 000 r/min，径向力为700 N，轴向力为1 000 N。

表1 不同波纹度情况下的主频率和谐波

表2 不同波形情况下的边带频率

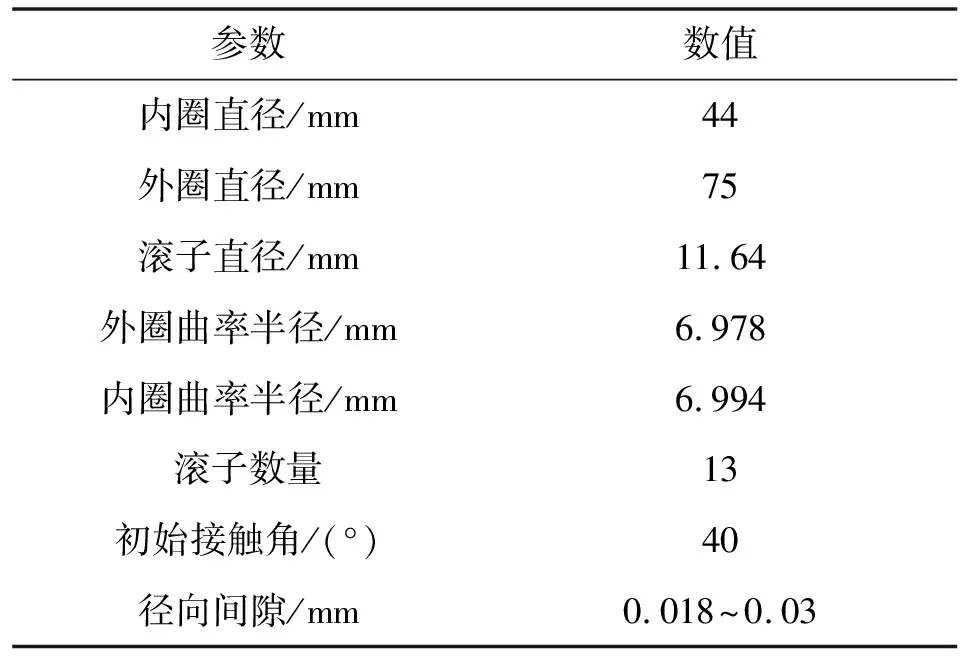
表3 轴承的几何参数

2.1 外圈波纹度(ORW)幅值对振动的影响

外圈波纹度(ORW)阶数为13，初始振幅为0.1 μm，幅值分别为5、6、7、8、9、10 μm，分别计算不同ORW振幅情况下的均方根(RMS)和峰峰值(PTP)，分析不同ORW幅值情况下柔性环和刚性环的振动。

对于柔性环和刚性环，当ORW的振幅为7 μm时，方向的轴承振动如图3所示。内圈的振动加速度谱如图3(a)所示，外圈加速度谱如图3(b)所示。当ORW幅值分别为5、6、7、8、9、10 μm时，计算了2个环加速度的统计值，对于内圈，统计值如图3(c)和3(d)所示,对于外圈，统计值如图3(e)和3(f)所示。在图3(a)—(b)中，当ORW阶数等于时，特征频率如表4表示。从图3(c)—(f)中可以看出：2个环的RMS值和PTP值随着ORW振幅的增加而增加。柔性环在转动过程中会产生不同的挠性变形，从而加剧了柔性环波纹度对振动的影响。因此，柔性环的振动比刚性环的振动更大。

表4 ORW的特征频率(Nw=13)

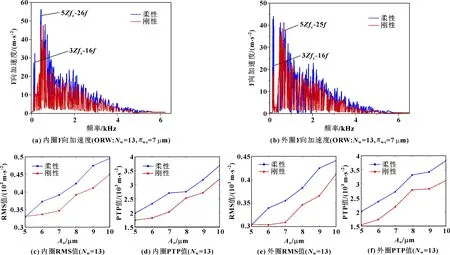
图3 外圈波纹度振幅对振动的影响仿真

2.2 内圈波纹度(IRW)幅值对振动的影响

内圈波纹度(IRW)阶数为13，初始振幅为0.1 μm，幅值分别为5、6、7、8、9、10 μm，分别计算不同IRW振幅情况下的均方根(RMS)和峰峰值(PTP)，分析不同IRW幅值情况下柔性轴承和刚性轴承的振动特性。

对于柔性环和刚性环，当IRW的振幅为7 μm时，方向的轴承振动如图4所示。

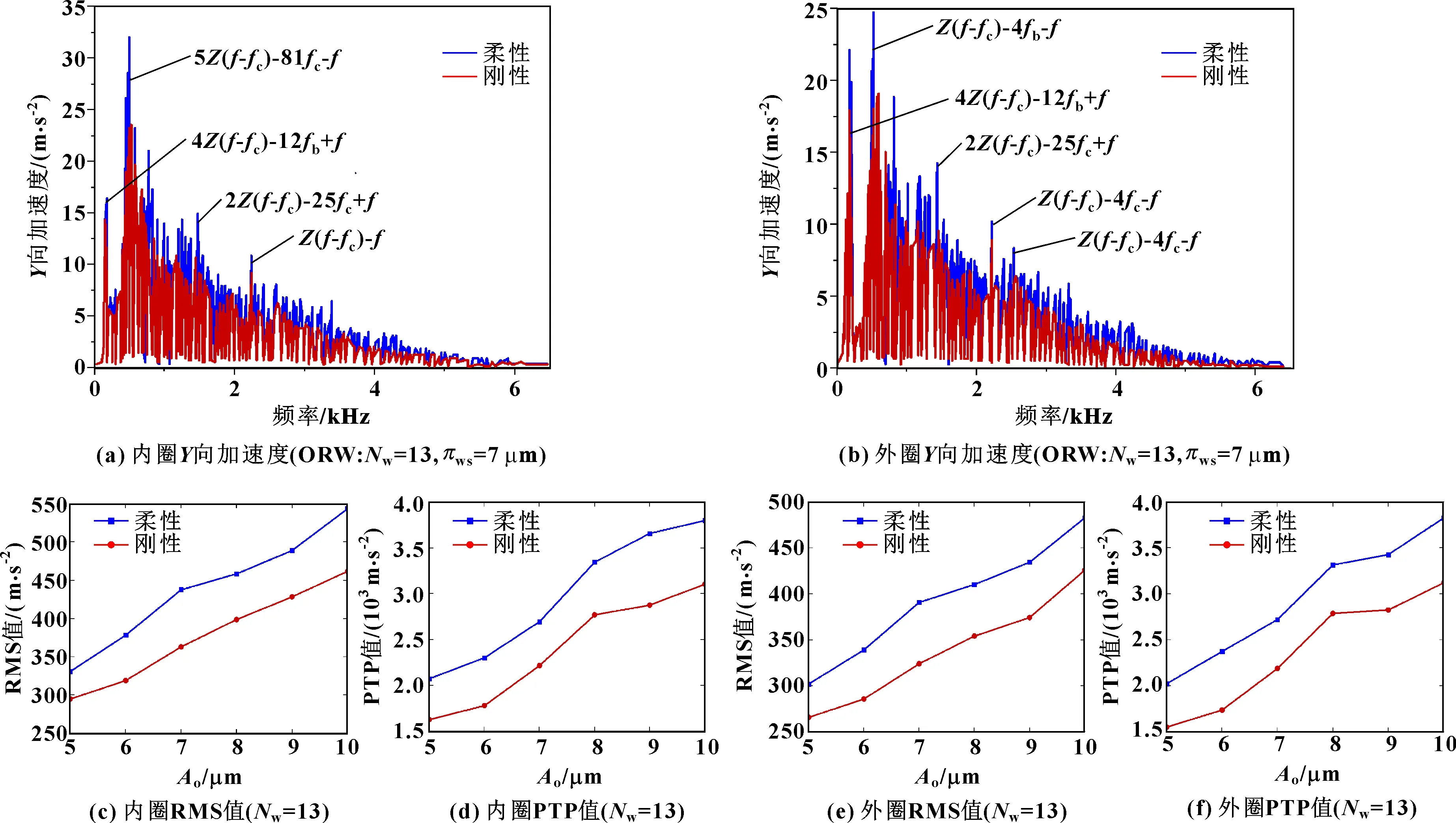
图4 内圈波纹度振幅对振动的影响仿真

内圈的振动加速度谱如图4(a)所示，外圈加速度谱如图4(b)所示。当IRW幅值分别为5、6、7、8、9、10 μm时，计算了2个环加速度的统计值，对于内圈，统计值如图4(c)和图4(d)所示,对于外圈，统计值如图4(e)和图4(f)所示。在图4(a)—(b)中，当ORW阶数等于时，特征频率如表5所示。从图4(c)—图(f)中可以看出：2个环的RMS值和PTP值随着ORW振幅的增加而增加，柔性环的振动比刚性环的振动更大。

表5 IRW的特征频率(Nw= 13)

3 实验验证

为了验证角接触球轴承的振动模型，进行了轴承振动测试实验，实验装置如图5所示。测试轴承安装在芯轴的非驱动端，2个径向加载装置以120°的角度加载在外圈上，轴向加载装置加载在内圈上。在外圈垂直方向和水平方向安装2个振动加速度测量头(灵敏度9.91 mV/)，用于测量外圈、方向的加速度。

图5 轴承振动实验台

在此实验中，轴承转速为1 800 r/min,方向径向力为150 N,方向轴向力为210 N，信号采样频率为20 kHz，采样时间为10 s。实验和仿真得到的外圈加速度频谱如图6所示。实验和仿真得到的轴向旋转频率分别为30、30.5 Hz。外圈的通过频率分别为189.7、190 Hz。内圈的通过频率分别为260.3、256.3 Hz。实验结果与模拟结果的、、分别相差约1.7%、-1.5%和0.16%，如表6所示。频率之间的细微差异可能是由于滚子的打滑或电机速度误差造成。

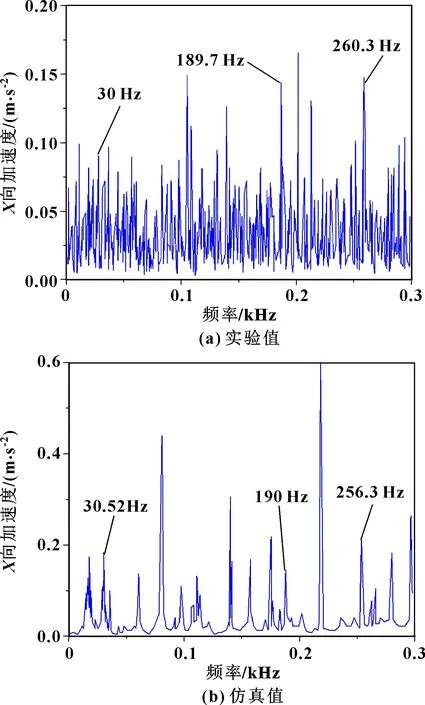
图6 加速度实验谱与仿真谱比较

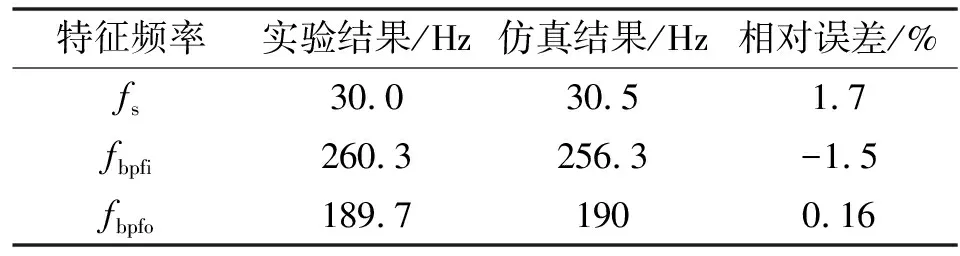
表6 实验和仿真结果

4 结论

建立了柔性角接触球轴承振动模型，考虑了波动幅值和波动阶数的影响。通过实验验证了振动模型的正确性，得出结论如下：

(1)柔性环在方向加速度的统计值小于刚性环体，分析原因是柔性变形减小了径向的振动。随着径向力的增大，角接触球轴承的振动随轴承转速的增加而增强。

(2)柔性环的振动更大。柔性环的PTP值和频率峰值均大于刚性环，分析原因是旋转过程中产生的柔性变形，加剧了波纹度对振动的影响。

(3)根据实验和仿真结果，外圈加速度频谱差异均小于1.7%，验证了动力学模型的正确性。